二战中德军坦克产量的有效估计——概率统计案例教学实践

陈 岩, 张 宁, 徐英杰

(1.沈阳工业大学 理学院,沈阳 110870; 2.沈阳化工大学 理学院,沈阳 110142; 3.沈阳工业大学 教务处,沈阳 110870)

0 引 言

实施数学长效教学模式一直是数学同行的一个美好的愿景,通过数学教育提升学生的思维创造力更是广大教育工作者的时代要求.概率论与数理统计(下称概率统计)不仅仅是一门应用数学课程,而且还含有一点哲学的味道(概率为零不见得不发生、实际推断原理等).其发展史[1]本身就是一部精彩纷呈的发现史,德·梅尔问题、赌资分配问题、蒲丰投针、贝特朗悖论等恰恰是探索、发现、分析、解决问题的著名案例,其概念、理论、方法的提出与完善本身就是针对概率问题不断发现、认识和完善的跌宕起伏、引人入胜的探索故事[2-6].

因此,将概率统计概念、理论、方法的产生过程、分析思考问题的逻辑、解决衍生问题的方法等引入教学,不仅可以将问题讲解得具体生动,而且可以培养学生的数学思维,对于培养学生发现问题、解决问题的能力均有极大的帮助.教师可以在教学过程中创设一种质疑、探究、讨论问题的自由氛围和环境,更好地展示解决问题的数学思维活动,培养学生直觉、猜测、类比、归纳和发散思维等科学研究能力[2-7],从而构建一种数学长效教学模式.

点估计是概率统计教学中的一个重点,通常情况下仅仅介绍矩估计法、极大似然估计法并辅以例题说明[8-9],教学内容抽象,较难理解.殊不知历史上Karl Pearson(下称老Pearson,矩估计法的提出人,1895年)与Ronald Aylmer Fisher(下称Fisher,极大似然估计法的提出人,1922年)就曾经为此在1936～1937年发生过激烈的争论[10-13].此外,1943年在第二次世界大战的反法西斯战场上,盟军情报部门正是基于极大似然思想的给出德军坦克生产量估计[14-15],为盟军制订反攻欧洲大陆战略计划提供了有力的情报支持,德军坦克生产量估计(下称德军坦克问题)遂成为统计领域-序估计的一个重要问题[16],而对这一问题的研究又恰恰是一个由理论走向实践的鲜活教学案例[14-17].

本文根据“德军坦克问题”的教学过程展开讨论,适度还原老Pearson,Fisher关于点估计的提出过程,完成矩估计法、极大似然估计法的有效构建和深度分析教学,提出基于案例探索解决实际问题的教学方法,尝试提高课堂教学效果、培养数学思维习惯,形成一种数学长效教学模式.

1 德军坦克问题

军事情报的一个重要目标就是准确了解敌方的军备情况,第二世界大战期间由于德军坦克在东线战场特别是1943年的哈尔科夫战役和库尔斯克战役中的突出表现,为了顺利开辟欧洲战场,当时盟国军队希望能够准确估计德军所能生产的坦克数量以做好反攻欧洲大陆的战争准备.

据悉为了准确掌握德军的坦克产量,盟军情报部门最初通过传统的情报窃取方式收集信息,得出的结论是从1940年6月到1942年9月期间每月生产1400辆坦克,然而这个数字显然与事实不符.后来,盟军发现每辆被俘获或被击毁的(下面简称被俘获)坦克上都有一个独一无二的序列号,为此盟军情报部门利用统计学方法构建了一个数学模型估计德军坦克每个月的产量,得出的结论是1940年6月到1942年9月期间每月生产256辆坦克.战争结束后,盟军从德国军需部长斯佩尔那里获得的德军坦克产量记录中看到德军每月生产255辆坦克.如今这一传奇故事成为了人们体验数学工作者们卓越工作的经典案例之一.

2 点估计法

当年盟军情报部门的原始工作现在已无从查起了,点估计方法应当是解决这问题的有力工具,现在来通过点估计方法教学看看破解这一问题的主要过程,探讨数学长效教育模式.

通常的点估计方法教学主要讲授矩估计法和极大似然估计法[8-9],为了有效地完成这一教学任务,首先布置课前准备:辛钦大数定律、依概率收敛、总体矩、样本矩以及契比雪夫不等式等概念、理论.其次,在完成矩估计法理论讲解后引入“德军坦克问题”.

2.1 矩估计法背景

追本溯源,事实上老Pearson在1895年提出矩估计法的时候[10],辛钦刚刚在俄罗斯出生(1894年出生),法国的Lebesgue还没有完整提出依测度收敛(事实上是1902年提出).这里首先向大家展示老Pearson 在1895年发表的“Contributions to the mathematical theory of evolution”文章,让同学们看一看老Pearson是如何提出点估计这一问题的,又是如何解决这一问题的.令人惊讶的是,老Pearson竟然是基于几何直观由利用二项分布与正态分布的关系,根据频率曲线方程(概率密度函数)的逼近提出各阶总体矩与同阶样本矩近似相等建立方程,提出矩估计法,这一工作在现在看来是多么的繁琐——不容易!但是直觉是灵感的源泉,归纳是思维的关键.至此,参数估计——点估计法由概念的提出到几何直觉再到归纳,形成一般性认识.

2.2 矩估计法及基于矩估计法求解德军坦克问题

今天怎么看待矩估计这一问题呢?借助辛钦大数定律以及依概率收敛概念,通过列方程组令各阶样本矩近似等于对应总体矩,给出参数的矩估计.至此矩估计法上了保险(理论保证),回归理性,多么简单!——时代进步.

那么对于实际问题——“德军坦克问题”是怎么处理的呢?怎样解决更合理呢?

这里,假设一个二战期间盟军的情报分析员获得了一些被俘获的德军坦克的序列号,现在将坦克序列号简化为编号从1到某个未知的最大值N(德军坦克总量),且不重复.假设被俘获的德军坦克有n辆,目标是通过被俘获的德军坦克的编号来估计德军坦克的总量N.设第i次获取被俘获的德军坦克号码为Xi,i=1,2,…,n,样本值(被俘的德获军坦克的编号)为xi,i=1,2,…,n.如何估计德军坦克的总数N?

假设每一个Xi的边际分布都是相同的P(Xi=k)=1/N, 其中k=1,2,…,N.

因此Xi的期望值就是

进一步

算例假设被俘获的坦克的编号为8,4,11,46,16,试估计德军坦克的数量.

显然,矩估计法所给出的估计量存在缺陷,即所得的估计量竟然比被俘获的坦克的最大编号还要小,有些尴尬.接着看看Fisher(1922年提出)的极大似然估计法处理这一问题的效果.先在课堂上详细阐述有关极大似然的思想,然后再分析这一问题.

2.3 基于极大似然估计法求解德军坦克问题

考虑到这一问题的特殊性,通过类比将离散变量连续化,即假设被俘获的坦克编号服从[1,N]上连续的均匀分布,也就是Xi～U(1,N),这在教材上是没有提到过的,现在尝试看看.

由均匀分布的性质可得其密度函数

进而构造似然函数

若

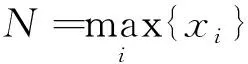
显然,根据算例这一估计量要比矩估计法得出的估计量合理.点估计中不同的方法就同一参数往往会得出不同的估计量,甚至同一种方法也可以得出不同的估计量,那么如何评判这些估计量呢?现在引入估计量的评价,通过给出无偏性、有效性概念来考察上述工作.

3 估计量评价

3.1 无偏性分析

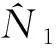
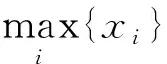
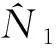
则

考虑到方差的实际意义,即方差是度量随机变量以其数学期望为中心的波动幅度的量,下面开展有效性分析.

3.2 有效性分析

显然,当n≪N时

其标准差

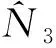
4 数值分析

假设德军有300量坦克,序列号为1到300,情况(i)俘获20辆坦克,情况(ii)俘获50辆坦克,试评估德军坦克的最大编号(产量).

模拟数据及计算结果如下:

(i) 第一组:编号为5,13,18,29,34,40,51,71,73,106,117,122,136,173,195,220,235,247,283,287.

第二组:编号为25, 56, 57, 89, 92,111,131,135,147,153,154,165,188,207,224,233,235,239,246,279.

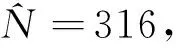
第三组:编号为52,59,63,68,69,70,91,106,114,131,142,160,166,177,187,194,244,254,263,282.

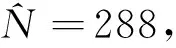
(ii) 第一组:编号为9,12,26,30,33,34,36,41,56,67,70,72,78,79,90,94,96,101,111,119,123,128,130,132,138,147,149,153,157,165,174,179,181,188,197,204,214,217,220,234,239,241,266,272,274,278,279,289,294,297.

第二组:编号为9, 10, 13, 18, 22, 26, 30, 40, 45, 51, 19, 53, 55, 60, 72,101,118,120,130,137,142,144,147,151,156,157,174,183,159,186,195,198,205,210,214,215,217,224,241,242,126,246,248,250,258,266,268,272,292,294.

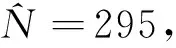
第三组:编号为7,10,33,37, 39, 47, 49, 52, 54, 58, 68, 76, 79, 80,88,91,94,104,29,111,113,116,126,127,128,129,139,145,162,169,175,176,177,179,186,194,180,200,201,210,211,220,246,248,257,264,265,272,295,300.

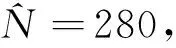
计算发现第一种方法得到的估计值出现了低于实际最大编号的现象,第二种方法得到的估计值比第一种方法得到的估计值更接近设定值,且当模拟俘获坦克数量越大估计值越接近设定值,这与结论相吻合.

5 结 论

无意间回到从前,让同学们穿越看到了一场数理统计初创时期神仙们打架的故事,窥见到了矩估计法、极大似然估计法的诞生过程.进一步,借助“德军坦克问题”的讨论探索了极大似然法的有效应用,看到了数学家帮助盟军击败德国人的方式.

通过探讨问题提出、问题解决的一般过程,结合实际案例激发了学生们探索、应用数学知识的兴趣,使得学生比较容易接受,为同学们开阔了视野,一定程度上起到了长效教学作用.因此根据问题背景精心设计展开的案例教学,不仅可以为课堂带来趣味性和启发性,而且还可以引导学生进行科学探索,训练数学思维,激发创新潜能,培养理性精神.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.