单向非贯通节理岩体滚刀破岩特性离散元模拟

陈晓坚

（厦门轨道建设发展集团有限公司，福建厦门 365004）

节理构造广泛分布于天然岩体中，按类型可将其划分为贯通与非贯通节理，其空间特征对岩体受力后的变形和失效方式具有重要的控制作用[1-3]。相较于贯通节理，岩桥的存在使非贯通节理岩体受力破坏过程更加复杂，故其也是众多学者研究的重点领域[4-5]。因此在滚刀破岩过程中，有必要针对非贯通节理特征对破岩特性的影响进行分析。

目前，滚刀破岩相关研究多是针对贯通节理岩体。在室内和现场试验方面：ROSTAMI 等[6-8]为研究TBM(全断面隧道掘进机)的开挖效率，开展了室内劈裂试验，总结了不同岩石层理面和滚刀侵入方向下的破岩效率；邹飞等[9]通过设计压头试验，研究不同节理倾角和间距组合下的岩石破坏类型，并分析了跃进点荷载的变化特征；王燕青等[10]利用双滚刀贯入试验，研究了不同节理倾角下岩体在滚刀作用下的红外温度特征，发现温度和岩体破碎特征具有对应关系；林奇斌等[11]为研究滚刀破岩裂纹扩展模式，制作了相应的水泥砂浆试件，发现节理位置对裂纹扩展具有重要影响；HOWARTH 等[12]利用线性破岩试验研究了不同节理倾角下的岩石破碎情况，并发现节理间距和破岩力成反比。

在数值模拟方面，翟淑芳等[13]采用广义粒子动力学法，分析了断续单节理倾角对破岩模式和效率影响规律；GONG 等[14-15]通过建立颗粒离散元模型，分析了破岩过程中裂纹随节理间距和倾角的变化特征；施雪松等[16]分析了节理倾角和间距对裂纹扩展路径及刀具受力等的影响；吴玉厚等[17]利用有限元模型分析了滚刀切削不同节理特征岩石的全过程，对其破碎效果进行了研究；周鹏等[18]以花岗岩为研究对象，建立有限元模型对不同滚压速度和节理特征组合下的滚动力及比能耗进行研究。

上述研究多以贯通节理岩体滚刀破岩过程为基础，通过改变节理倾角、节理间距、贯入度等参数对裂纹扩展特征、破岩力等进行分析。然而，对于力学性质更加复杂的非贯通节理岩体滚刀破岩过程的研究却十分缺乏，故本文采用PFC2D软件建立单向非贯通节理岩体滚刀破岩离散元模型，以岩桥长度和倾角为变量，分析岩体破碎模式、法向力、裂纹数及比能耗等参数，对非贯通节理岩体滚刀破岩特性进行研究。

1 滚刀破岩数值模型

1.1 滚刀破岩特征

现阶段，滚刀在破碎完整岩体时的应力分布及滚刀荷载计算理论已较为成熟，故本文以其为参照开展单向非贯通节理岩体滚刀破岩离散元数值模拟试验，比较分析节理岩体破碎过程中的差异化特征。在滚刀破岩过程中，自由面附近岩体受到刀刃碾压而发生破坏，其颗粒较小呈粉状，称其为“密实核”。滚刀继续侵入时，密实核以静水压力的形式将滚刀荷载均匀传递到周边区域，当内部岩石所受应力大于其强度时便会产生中间、侧向及径向裂纹等。侧向裂纹多与岩石自由面相交，径向和中间裂纹则会随贯入度的增加向岩石内部扩展[19-22]。由上文可知，岩石变形和裂纹产生的主要原因是岩石中的应力，若将滚刀荷载视为线荷载，则岩石中的应力分布如图1 所示，即应力最大处位于荷载作用线上，而离作用线越远，所处位置越深，则应力越小[23]。

图1 线荷载下的岩石内部垂直应力分布特征Figure 1 Distribution characteristics of internal vertical stress in rock under line load

1.2 岩体参数标定

颗粒离散元能够从细观力学的角度对岩石的损伤破坏机制进行研究，因此被广泛应用于岩石力学相关分析中。PFC2D颗粒流计算方法通过对颗粒细观参数和边界条件进行定义，进而实现对实际物理原型的模拟过程。基于MOON 和赵国彦等[24-25]的研究，本文采用单轴压缩、巴西劈裂及直剪试验对离散元颗粒的细观参数进行标定。花岗岩岩石宏观物理力学参数见表1，标定后的细观参数见表2。

表1 岩石试样宏观力学参数Table 1 Macroscopic mechanical parameters of rock samples

表2 岩石试样细观力学参数Table 2 Micromechanical parameters of rock samples

1.3 离散元模型建立

滚刀破岩过程中，刀盘与掌子面紧密贴合，在刀盘转动时，滚刀同时发生两个方向的运动，即绕刀盘中心轴转动和绕自身轴线转动。在此过程中，一般认为滚刀对岩石产生三个方向的作用力，即法向力、滚动力和侧向力。相关研究表明[14-15]，裂纹的产生和扩展主要受到法向力的影响，可以将三维的滚压破岩过程简化为二维的垂直压入过程。因此，本文利用PFC2D程序建立如图2 所示的单向非贯通节理岩体滚刀破岩离散元模型。

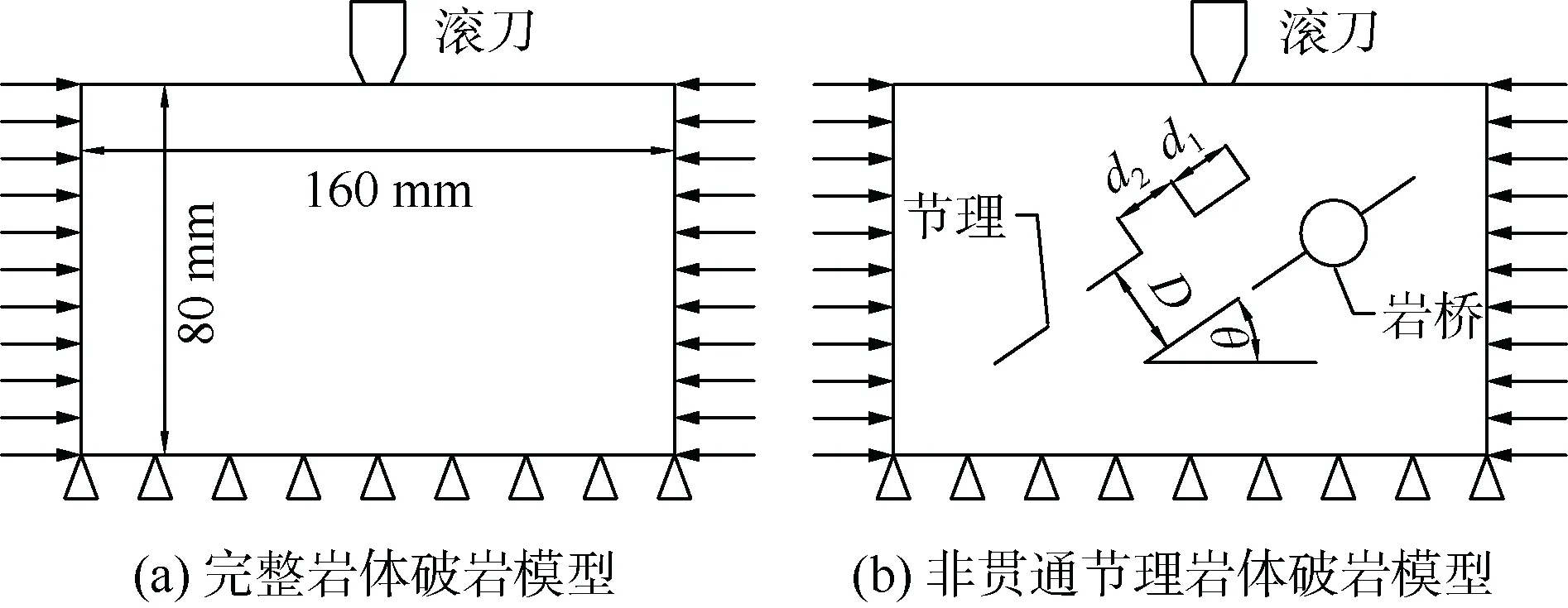
图2 滚刀破岩离散元模型示意Figure 2 Schematic diagram of discrete element model of hob rock breaking

为避免边界效应带来的不利影响，将模型尺寸设置为160 mm×80 mm，模型左右侧施加恒定围压σ0(5 MPa)，顶部为自由面，底部施加固定约束。滚刀类型为盘形滚刀，刀刃宽度取5 mm，刀刃角为20°。本文不考虑滚刀的变形和磨损，故视其为刚体，采用wall 单元对其进行表征，并对其施加恒定的贯入速度0.01 mm/s，贯入度取值均为5 mm。模型中设置6 条两两平行的单向非贯通节理，每条节理的长度均为15 mm，宽度为1 mm，节理生成手段为在模型指定位置生成一定长度和厚度的墙体，并删除墙体区域内的颗粒，该方法可以使节理更加规则，降低了离散性，使试验结果更加可靠。试验过程中，节理倾角θ取值范围是0°、30°、45°、60°、90°，岩桥长度取值为5、10、15、20、25 mm，节理间距取定值20 mm，同时设置一组完整岩体破岩试验作为对照组。依据以上试验设置，开展相关数值模拟工作。

离散元模型中的颗粒接触类型为线性平行黏结模型(linear parallel bond model)，该模型提供了两个界面的行为：一是无穷小的线弹性(无张力)和摩擦界面承载一个力；二是有限大小的线弹性和黏结界面承载另一个力和力矩(见图3)。第一个界面与线性模型等价，不抵抗相对旋转；第二个界面称为平行黏结键，当其黏结时，能够抵抗相对旋转，其行为为线弹性，直到超过强度极限，黏结键断裂。

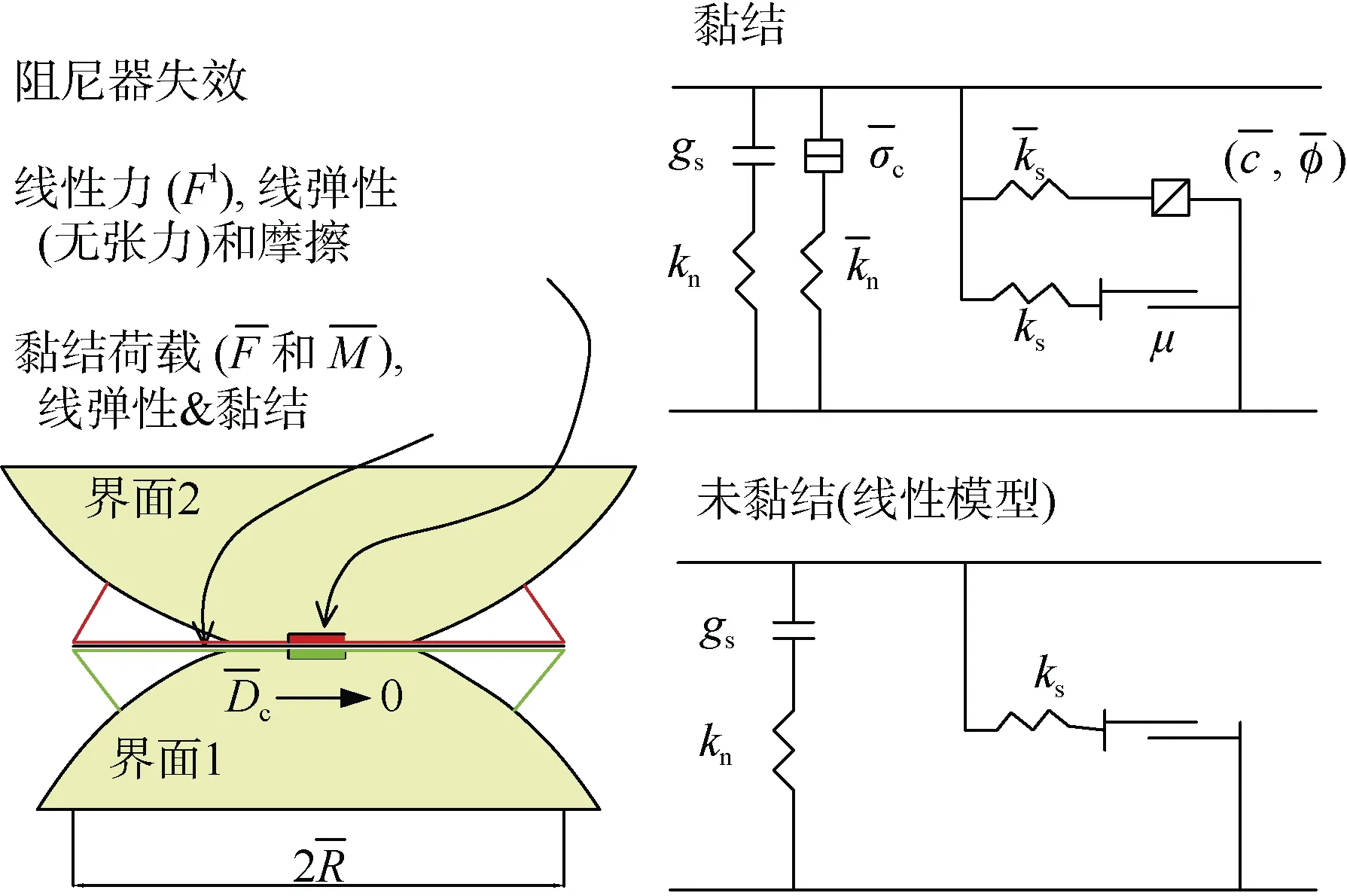
图3 带有非激活阻尼器的线性平行黏结键模型Figure 3 Linear parallel bond model with inactive dampers

2 数值试验结果分析

2.1 岩桥长度和倾角对岩石破碎的影响

基于上述试验设置开展滚刀破岩数值模拟工作，对模拟过程中各岩桥长度和倾角组合下的裂纹扩展形态进行统计，具体如图4 所示。首先横向分析各岩桥长度下裂纹扩展随节理倾角变化特征：岩桥长度为5 mm时，在0°倾角下，裂纹在连通上部3 条节理后，随贯入度增加，密实核周边岩体已充分破碎且内部积聚着较大的应变能，裂纹有继续扩展的趋势，故向下继续延伸至下部节理端点；倾角为30°时，左侧上部节理与刀刃距离较近，故破坏充分，而多余的应变能促使裂纹继续扩展至右侧节理各端点处；倾角为45°和60°时，由于两侧节理上部向刀刃位置进一步靠近，在较小的贯入度下左侧上部节理发生破坏，故有较多的能量支持侧向裂纹的扩展，进而导致侧向裂纹宽度和数量有明显增加；倾角为90°时，侧向裂纹扩展过程中受到节理限制，有向节理中间区域扩展的趋势，故其裂纹分布范围明显小于以上工况，整体较为集中；在岩桥长度为10 mm 至25 mm 时，裂纹分布随节理倾角的变化规律与岩桥长度为5 mm 时基本一致。从纵向来看，随着岩桥长度的增加，裂纹扩展区域整体上呈现缩小趋势，但图4(e4)、(e5)较图4(d4)、(d5)中的裂纹范围有明显增加，主要原因是岩桥长度为25 mm，节理倾角大于60°时，上部节理位置已经越过自由面，即只需较小的贯入度便可使上部岩石发生破坏，故相比于岩桥长度为20 mm 时，裂纹分布区域有明显增加。节理位置对裂纹扩展具有明显的“导向作用”，有多条节理时，裂纹扩展方向总是趋于距离其最近的节理。

图4 不同岩桥长度和倾角组合下的岩石破碎形态Figure 4 Rock fragmentation morphology under different combinations of rock bridge length and dip Angle

对岩桥长度为5 mm 时不同倾角下的裂纹分布及接触力链特征进行分析，具体如图5 所示。从图中可以明显发现颗粒受力较大部分集中在节理位置处，倾角为90°时最为显著，而完整岩体力链分布则较为均匀，整体以刀刃位置为中心呈辐射状分布；从裂纹末端位置来看，几乎所有裂纹末端都处于节理端点处，同时该处力链明显较粗，出现了显著的应力集中。通过接触力链分布情况再次证明了节理的“导向作用”。

图5 d2=5 mm 时接触力链随节理倾角的变化特征Figure 5 Variation characteristics of contact force chain with joint dip Angle when d2=5mm

应力水平及其分布情况也是岩石破坏过程中的重要参数，现对岩桥长度为5 mm 时各倾角下的岩石内部应力特征进行分析，具体如图6 所示。可以发现，各工况下的应力水平随节理倾角增加呈现先增大后减小的趋势，在45°倾角下达到最大值。由图4 可知，45°和60°倾角下的裂纹集中程度明显大于其他组合，裂纹扩展对于应变能的耗散较少，故其应力水平较高。同时发现，完整岩体内部应力分布较为均匀，整体上和图5 较为符合；90°节理倾角下的应力则趋向于竖向分布，主要原因是竖向节理限制应力向侧方扩散；其他应力区形状受到倾角变化的影响亦与其基本保持一致。结合前文发现，裂纹形态、接触力链特征及竖向应力分布三者之间具有较好的吻合度，也说明了相关分析的合理性。

图6 d2=5 mm 时竖向应力随节理倾角的变化特征Figure 6 Variation characteristics of vertical stress with joint dip Angle when d2=5mm

2.2 破岩力变化特征

滚刀破岩力是TBM 掘进过程中的重要参数，其关系到破岩效率、刀具工作状态等众多方面。本文基于上述数值模拟内容，采用HISTORY 命令对滚刀破岩过程中的法向力进行采集并计算其峰值和均值，对法向力随岩桥长度和节理倾角的变化特征进行研究，详见图7。图7(a)为不同岩桥长度下法向力峰值随节理倾角变化曲线，可以发现岩桥长度为5、10、15 mm时的曲线变化趋势相似，总体上呈现先增大后减小再增大的趋势；而岩桥长度为20、25 mm 时的变化趋势相似，呈现先减小后增大再减小的趋势；图7(c)中对应的法向力均值曲线则总体呈现先增大后减小的趋势，但是岩桥长度为25 mm，节理倾角为90°时，法向力均值却突然升高，主要原因是此时岩桥长度较大，上部节理越过自由面，导致小贯入度下上层岩石和节理发生破坏，节理变形对于应变能的耗散大大降低，故导致其法向力大于其他组合。图7(b)为不同节理倾角下法向力峰值随岩桥长度变化曲线，在节理倾角为0°、30°时的法向力曲线变化趋势具有一致性；倾角为45°、60°、90°时的法向力整体水平较为接近，且在岩桥长度为20、25 mm 时的法向力明显高于前面二者，结合裂纹扩展情况分析可知，当倾角较大时上部节理与刀刃距离更小，其更容易在小贯入度下发生破坏，此后应变能聚集，裂纹在小范围内扩展，岩石内部应力水平较高；图7(d)为对应于图7(b)的法向力均值曲线，发现节理倾角90°时的法向力曲线明显异于其他倾角，结合上文接触力链图可知，90°倾角下的应力传递路径与节理平行，完全不同于其他工况，故导致了不同曲线的差异性。总体上说，完整岩体法向力均值和峰值均大于节理岩体，体现了节理对于破岩过程的促进作用，而法向力曲线和裂纹扩展形式、应力分布特征等具有较好的关联性，也间接说明了各部分数据的有效性。

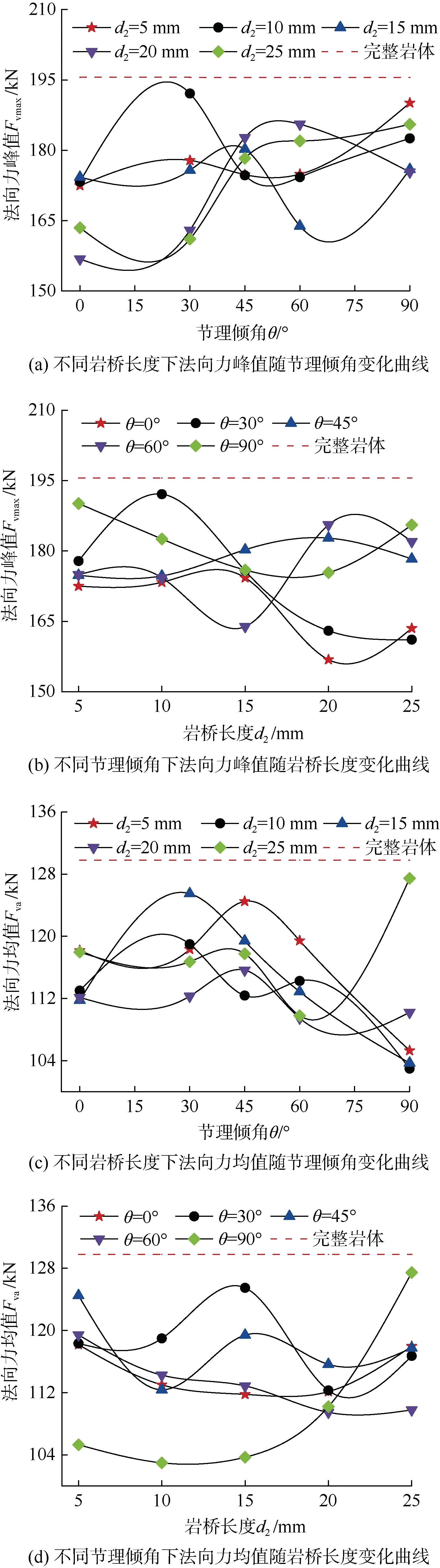
图7 不同岩桥长度和倾角组合下的破岩力曲线Figure 7 Rock breaking force curves of different rock bridge lengths and dip angles

2.3 裂纹数

裂纹相关参数直接影响到破岩过程中岩片的形成，结合上文各工况下的裂纹形态对裂纹数量进行分析(见图7)，有助于了解各节理参数对于比能耗的影响规律。图8(a)、(b)分别为不同岩桥长度下裂纹总数随节理倾角变化曲线及不同节理倾角下裂纹总数随岩桥长度的变化曲线，对比图7(c)、(d)可以发现，法向力均值曲线和裂纹总数曲线具有高度一致性，说明破岩过程中的滚刀受力和裂纹扩展高度相关，可以从宏观层面的受力大小研究微观层面的裂纹数量。同时发现，完整岩体内部裂纹数整体大于节理岩体，主要原因是缺少节理的“导向作用”，完整岩体裂纹区发生过度破碎，裂纹细密而破碎岩片体积较小；岩桥长度为5 mm，节理倾角为0°、45°、60°时，岩体内部裂纹数量却大于完整岩体，分析其原因可能是在这3 种工况下，由于岩桥长度及节理与刀刃的距离均较小，裂纹能够连通两侧节理且在节理端部出现了较多的细小裂纹。从图8(c)、(d)则可以看出拉裂纹数远大于剪裂纹数，岩体破坏以张拉破坏为主。

图8 不同岩桥长度和倾角组合下的裂纹数曲线Figure 8 Curves of crack number under different combination of rock bridge length and dip Angle

2.4 比能耗

滚刀破岩效率是TBM 掘进过程中的重要参数，一般用比能耗对其进行表征，即产生单位体积岩片所损耗的能量，有

式中，SE 为比能耗，J/m3；WV为垂直力FV做功，J；WR为滚动力FR所做功，J；FV为滚刀垂直力，N；FR为滚动力，N；J为破岩距离，m；h为贯入度，m；V为破碎岩片体积，m3。

对裂纹形态起决定性作用的是垂直侵入过程，所以本文重点分析法向力，对比能耗公式作如下简化：

由于本文数值模拟过程中，贯入度h为定值(5 mm)，因此需要对各工况下的法向力曲线和破碎岩石体积进行采集，将采集的数据代入式(2)得到不同岩桥长度和倾角组合下的比能耗曲线，具体如图9 所示。首先可以发现，完整岩体比能耗值明显高于节理岩体，和上文呼应，从正面说明了节理对于破岩过程的促进作用。各工况下的比能耗曲线和破岩力均值曲线具有很好的对应关系，0°、60°、90°节理倾角下的比能耗值明显低于其他节理组合，且曲线较为平滑，60°倾角下整体呈减小趋势，0°、90°下呈先减小后增大趋势，前者在岩桥长度为25 mm 时取得最小值，而后者在岩桥长度为15 mm 时取得最小值，通过和前文裂纹扩展图对比可以发现，比能耗最小值对应的工况下侧向裂纹和自由面连通后形成的岩片体积较大，因而破岩效率较高。同时可以发现，岩桥长度为25 mm、节理倾角为90°时，比能耗值很大，几乎等于完整岩体对应的比能耗值；由上文可知该工况下的岩片体积相对于其他工况并不小，因此推测造成其比能耗值远大于其他工况的原因是其应力水平较高(法向力均值较大)，法向力的增幅领先于岩片体积。因此，在提高破岩效率时，不能单纯追求岩片体积的增加，还需要考虑其应力水平的大小，在安全的前提下提高TBM 掘进效率。

图9 不同岩桥长度和倾角组合下的比能耗曲线Figure 9 Specific energy consumption curves of different rock bridge lengths and dip angles

3 结语

本文采用颗粒离散元法建立了单向非贯通节理岩体滚刀破岩模型，通过对不同岩桥长度和倾角组合下的破岩参数进行分析，研究非贯通节理岩体滚刀破岩特性，得到以下相关结论。

1) 裂纹形态受节理位置影响较大，节理对裂纹扩展具有明显的“导向作用”；当岩体中存在多条节理时，裂纹扩展方向总是趋向于和其距离最近的节理。

2) 各工况下岩体内部的竖向应力水平随节理倾角增加呈现先增大后减小的趋势，在45°倾角下达到最大值；应力区形状受到节理位置影响，两者具有一致性。

3) 完整岩体法向力均值和峰值均大于节理岩体，节理对于破岩过程具有明显的促进作用；拉裂纹数远大于剪裂纹数，岩体破坏以张拉破坏为主。

4) 0°、60°、90°节理倾角下的比能耗值明显低于其他节理组合。60°倾角下呈减小趋势，在岩桥长度为25 mm 时取得最小值；0°、90°下呈先减小后增大趋势，在岩桥长度为15 mm 时取得最小值。

在提高破岩效率时，不能单纯追求岩片体积的增加，还需要考虑其应力水平的大小，在保证安全的前提下合理提高TBM 掘进效率。