论电磁学中的负波速和超前波

黄志洵

（中国传媒大学通信与信息工程学院，北京 100024）

1 引言

波动是大自然中常见的现象，例如田野中的麦浪，海洋中的海浪。当然，电磁波是非常重要的一种波。所谓物质必须具有质量，因此波本身不是物质，而是物质运动的一种外在表现形式。Newton 的经典力学研究质点的运动，范围扩大到地面上的物体和宇宙中的天体。Newton 力学的用途无所不在，但它并不能概括波的运动。实际上，Newton 没有研究过波动。波动是一种无固定形状和确定质量的物质运动的外在形式，它不能用Newton 力学作精确地描述。例如，不能在Euclid 空间中找到其运动轨迹，也不能用力使之加速。在现代电磁场与电磁波的理论中，用算子理论与波函数空间来对其运动状态作描述，这与宏观物质的处理很不一样。

关于负波速，必须指出M.Born和E.Wolf[1]在其名著《Principles of Optics》中指出，波动的速度（相速、群速）是标量而非矢量。遗憾的是，有的物理学家对此并不清楚，一味坚持“负速度就是运动方向相反”。

“负速度”在Newton 力学中表示运动方向相反，在波动力学中却不同。虽然Einstein[2]（在1907 年）、Sommerfeld[3]（在1914 年）和Brillouin[4]（在1960 年）都讨论过负速度问题，但他们的理论或有错误，或不全面；今天有必要重作论述。另外，虽然早在1945 年J.Wheeler 和R.Feynman[5]即指出了Maxwell-Helmholtz波方程的超前解不应随便抛弃，但他们当时也不敢说会有单独的超前波存在。在今天，我们知道确有负速度的波，特别是，2009 年N.Budko[6]以实验发现了天线近场区的负速度，现象是在自由空间中发生的，并不依靠反常色散媒质之类的物质。

既然波动是物质运动的独特表现，目前对波速度就要有新认识。波速研究是波科学探索的一个重点和突破口。本文认为超前波存在，而负波速是超光速的一种特殊形态。对于超前波，本文将其定义为“具有负速度的波动”。

2 电磁场分析中的平面波谱法

现在我们略述天线问题求解方法与超前波之间的关系。几十年前天线振子的计算曾经引起中国科学界的重视。1969年秋天，中国与苏联的关系十分坚张，战争似乎一触即发。该年10 月，中国政府针对广播通信系统的安全召开会议，检查战备工作。会议的决定之一是要求科学家解决缩小天线尺寸的问题，因为巨大的天线是难于隐蔽的。中国科学院建立了天线计算组，针对偶极天线展开数值计算研究。首先想到的是Maxwell 波方程的求解。计算内容包括：①近区——振子附近的远小于波长的区域；②远区——距离振子几个波长及更远的区域。严重的问题是波方程有汇聚和发散两套解，怎样提示计算机向外的发散解? 在解析处理时这就是著名的Sommerfeld边界条件。数值计算中应当怎么办? 后来有人建议直接求解1 阶Maxwell 方程组的初值问题，直到取得定态解。这样就只需在无限远处加上零场条件，绕开另一个边界条件。……传统的天线计算方法是，先给定振子上的电流分布，再用推迟势的积分表达式求辐射场及振子参数。严格的数值计算（使用当时的高速大容量电子计算机）的研究一直不够，特别是要从天线所处原点考虑到远场（理论上是无限远），是比较困难的。一个根本问题是，从波方程出发好，还是从基本的电磁场方程出发好?

在自由空间中，若无电荷源（体电荷密度ρ=0），也没有电流源（电导率σ=0 或电流密度矢量J=0），电磁波方程可写作：

式中E、H是电场强度矢量和磁场强度矢量；在单色简谐波条件下，取ejωt为波动表达方式，则∂/∂t→jω，∂2/∂t2→-ω2，得到矢量Helmholtz方程：

式中

为了作具体化的讨论，我们可以取一付电偶极子作为天线（在中央馈电），并考虑远区场和近区场方面的有关问题。图1 表示电偶极子天线及场强测量平面。

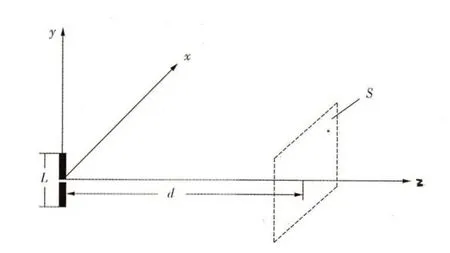
图1 偶极天线与近场测量平面

我们现在对电场强度求解。在r≥0 的地方有一个解：

式中k是波矢量，r是位置矢量。类似地对磁场可导出：

式中kx、ky是波矢的分量，满足以下关系：

因此可求kz；若，则有

虚数的kz将对应一个平面波消失波谱（Evanes‐cent Plane Wave Spectrum，PWS），其特点是从源所在地开始随r的增大而急剧衰减；而这个PWS 可由z=0平面的边界条件而确定。

在以上各式中，F是一个矢量函数，我们对它不展开讨论。但在这里要考虑近场测量、近场与远场关系、消失场影响等问题。突出之点是如何从理论上计算消失态（Evanescent State）影响。上世纪90 年代曾发展近场测量技术，这种平面扫描近场测量技术为确定天线方向图及其参数提供了一条既经济又准确的途径，它的理论基础是场的平面波谱描述方式。天线远场方向图与PWS 之间有简单关系；在多数应用中，由近场测量数据经过Fourier变换可得远场方向图。

现在可在图1所示的平面作planar scanning，其中d是在近区内。在该平面处有

式中

可以看出Ey（x,y,d）与F′y(kx,ky)是一个Fourier变换对；当z=0时有

因而Ey(x,y, 0)与Fy(kx,ky)是另一个Fourier 变换对。

以上提供了理论基础；由于使用计算机模拟，可用PWS 法计算偶极天线的孔隙场分布（Aperture Dis‐tribution）。选择测量平面靠近天线，故消失波包含在近场测量之中。消失态近场行为虽对远场方向图无影响，对于准确建模于近场却重要。上述原理已在实验上有过实证。

基于电磁波方程（本文的（1）式和（2）式），加上边界条件就成为2阶椭圆型偏微分方程的边值问题。由于一些数学和物理上的原因，循此途径去计算有困难。1977 年中国科学院物理研究所和计算技术研究所联合发表的论文分析了产生困难的原因，指出在解析处理时已趋向无限远的。……最后选用的计算方法是从Maxwell 方程组（一阶双曲方程组）出发，直接离散化，使初值问题成为有效的算法。

本文认为中国科学界的上述早期工作是有益的。但在当时科学家们未能认识到会聚波解，并不能随便将其“排除”。这就是笔者所说的，它是Maxwell 波方程的一个解，! 在笔者看来，波方程有两套解不是什么“严重的问题”，而是大自然的特性之一。自然界似乎比人们所能想象到的还要奇怪，但我们必须按照她的本来面目去认识她。

3 电磁场的势函数分析与D’Alembert 方程的解

静态场分析中有引入标量电势函数、标量或矢量磁势函数的作法，可使场的分析简化。对交变电磁场而言这方法更为重要。矢量代数中，对任意矢量A有∇·∇×A=0，而Maxwell方程组中有一个方程是∇·B=0；故可定义矢势A，其依据为

考虑到Maxwell 方程组中有一个式子：∇×A=-∂B/∂t，故可得

但在矢量代数中，对任意标量Φ 有∇× ∇Φ=0，故可取

故得

因此由矢势A和标势Φ 可决定E；根据B=∇×A可知，由A可决定B；这就是引入势矢量函数决定电磁场的基本概念。

但为了唯一地确定A、Φ，还须知道∇·A的值。这有随意性，例如Lorentz给出

式中v是波速(v=1/)，故上式也写作

这叫Lorentz 条件。把B和E的公式代入Max‐well方程并引用Lorentz条件，可以证明有下述偏微分方程成立：

以上两式表明，A的源是电流密度矢量J；Φ 的源是体电荷密度ρ；以上二式统称D’Alembert 方程。为分析问题方便，可先只考虑函数Φ 的标量方程。假定电荷源是点电荷q（t），则可证明解答Φ 可表为以下形式：

在这里v可以是光速（c），也可以是不同的值。上式等号右边首项表示在t时刻空间点P（x,y,z）处的情况取决于t之前，即时源点电荷的大小，故空间点滞后于源，这是（Retarded Potential）现象。第二项表示P 点的情况取决于t之后，即时刻的源电荷的大小，空间点领先于源，是（Ad‐vanced Potential）现象。后一项在过去的教科书中都说应当去掉，因为“波从外部向源会聚是不可能的”，解释不了波的来源。况且它意味着负速度，亦即

而负速度在过去只表示“运动方向相反”，而非其值真的为负。如速度值本身就是负的（与矢量方向无关），则不符合因果性（Causality）要求，即因必先于果，而非果先于因。今天来看，这些观点都是有争议的!

4 负速度与超前波概念的意义

超前波本来是电磁理论中的预言，近年来有了实验证明，或者说实验的发展超越了理论上的预期。2013年笔者的论文“电磁波负性运动与媒质负电磁参数”发表[7]，提到超前波概念最早来自J.Wheeler 和R.Feynman[5]的早期论文。1940 年Feynman 向Wheeler指出，空间中一个单独电子不会有辐射，只有同时有源和接收者时才会有辐射。他分析了只有两个粒子的情况，向Wheeler提问说：“这种一个影响另一个，而又反作用回来的力，是否能解释辐射阻尼(Radiation Resistance)?”Wheeler 建议向这个双电子模型引入超前波概念——过去这种Maxwell 方程的解未受重视。Wheeler 和Feynman 把这概念发展为电子与周围的多个“吸收者”（Absorbers）之间的关系，即把辐射阻尼看作是由吸收者们的电荷以超前波形式对源的反作用；现在他们的理论有了对称性，但必须用只是出现了新的困扰——其在发射之前即回到了源头。但他们取人们习惯的迟滞波，以适当方式与超前波彼此抵消，从而避免了令人不快的矛盾；前提是所有辐射都保证在宇宙某处、在某时间会被吸收。这证明他们尚不敢单独使用超前波的概念。

Wheeler-Feynman 所论述的向内运动的波（时间上倒转运动的波），其实就是我们现在讨论的负速度。在波科学中有两种表现形式——负相速（Negative Phase Velocity, NPV）和负群速（Negative Group Velocity, NGV）。过去在研究截止波导理论时笔者曾发现相位常数为负（β＜0）的现象[8]，这实际上是一种超前波，后来由英国学者提出了实验证明[9-10]。vp＜0 当然表示相折射率为负（n＜0），但这并不表示超前波必须纳入超材料（Meta-Materials），即左手材料（（Left-Handed Material，LHM）的框架内才能理解。在普通物质材料条件下也有超前波现象，也见诸于一般天线的近场物理状态之中。例如2009年N.Budko[6]发表论文“自由空间中电磁场的局域负速度观测”，其理论与实验表明，矢量电磁场的近场、中场动力学比简单的“向外传播”要复杂许多。存在一个靠近源的区域，在那里波前以光速向外行进，波形的核心主体却向内，即逆时而行，亦即（travel back in time）。该文给出了negative waveform velocity 的实验观测，认为发现了近场区的负速度，而且在（3.5～8）mm 的头5 个近场波形，显示内峰对时间逆行。因此，即使没有媒质，在自由空间中电磁波也可能以行进。

2013 年笔者提出了“电磁波负性运动”的概念[7]，并将其与简单的“反向运动”相区别。文章认为应当把它看作自然界所固有的正常物理现象。

Wheeler想确定如果推迟电磁波和超前电磁波总是均等发生，将会发生什么。尤其是，这意味着无线电发射机把波动一半功率发射至未来，把另一半发送到过去。可以认为所有的超前电磁波都从观察中消失，其理由如下：当来自地球某一特定波源的推迟电磁波在太空中扩散并遇到物质时，它们就会被吸收。这个吸收过程包含了电磁波引起的电荷干扰，结果远处的电荷因而产生了次级辐射。根据这个理论的假设，这种辐射同样也是一半为推迟辐射波，一半为超前辐射波。这个次级辐射的超前辐射波分量，向时间的反方向传播，其中的一部分传播到地球的发射源。这个次级辐射波只是波源的一个微弱反射，但是，这类来自太空的不计其数的微弱反射波能够产生巨大的叠加效应。可以证明在某些条件下，可以用于加强初级推迟波，使它达到最大强度。同时，由于干涉的抵消作用，波源的超前辐射波分量却被消除了。在时间的尽头，当所有的这些波及其向时间的正反两个方向运动的电磁波和反射波叠加在一起时，产生的净效应呈现出纯粹的推迟波辐射。

P.Davies[11]认为，Wheeler-Feynman 上述理论有个前提：宇宙中有足够丰富的物质能够吸收进入到太空中的所有辐射，亦即对于所有的电磁波宇宙是不透明的。这是一个严格的条件。从表面判断，对于很多不同波长的波宇宙似乎是完全透明的，否则我们看不见遥远的星系。另一方面，吸收过程不存在时间限制，因为超前（向时间的反方向）反射波能够反向在时空中传播，同时对它们来讲，从遥远的未来向回传播与从不久的将来向回传播同样容易。所以，这个理论是否成功体现在一个向外传播的电磁波能否最终在宇宙的某个地方被吸收。

Davies 说，我们不知道情况是否真的如此，因为我们不可能预知未来。但是，我们能够推断宇宙目前发展的趋势，结果似乎是否定的——即宇宙不是完全不透明的。这似乎否定了Wheeler-Feynman 的思想，但还存在着某种令人好奇的可能性。假设宇宙中存在足够多的物质来吸收大多数辐射，但不是吸收全部辐射。按照Wheeler 和Feynman 观点，这将导致超前电磁波的不完全抵消。难道可能是这样的情形：有一些超前电磁波“走入过去”——或者来自未来——但它们的波强度太低，所以我们还没有发现它们？

现在笔者必须说，Wheeler-Feynman（以及Davies）的某些观点是我们不能同意的。例如说超前波总会被迟滞波抵消，这样就不会有单独的超前波。近年来的实验（多数在1998年以后）使我们更加确信，已由众多NGV实验和天线近区场，它不会被抵消掉。而且从逻辑上讲，为什么总是超前波被抵消，迟滞波就不会被抵消？这是说不通的。前述3位科学家是受时代的局限才那样讲，现在我们把超前波和负速度作统一的理解。

人类为了改善生活和探索宇宙，对宏观物质运动速度的提高作了不懈的努力；同时也在微观领域进行探索，研究近光速、超光速的粒子动力学。例如深入开展关于负速度和超前波的探索。

5 许多负群速实验的成功是超前波存在的证明

经典波速理论的奠基者是A.Sommerfeld 和L.Brillouin，在1914 年[3]提出的经典波速理论。1960 年Brillouin[4]给出了以该理论为基础作计算得到的c/vg～f关系曲线，清楚地显示了vg由正变负的过程。Brill‐ouin 说：“This curve presents a curious anomaly in the absorption band,c/vgcan become less than 1, and even less than zero. This means that the group velocityvgcan be greater than the velocity of lightc, can be infinite and even negative!”

关于光脉冲传播奇特的NGV 物理现象，最早提出者是C.Garrett[12]。这是理论分析而非实验工作。他证明即使在强反常色散时（vg可大于光速c甚至为负）仍可用群速概念，并对时间超前现象作了解释。1982年S.Chu[13]的论文最早以实验证明NGV 存在，实验结果完美地给出了（vg＞0,vg=∞，vg＜0）这样3 种状态，与1960 年Brillouin 提供的计算曲线十分相似。他也指出，when the peak of the pulse emerges from the sample at an instant before the peak of the pulse enters the sample.

经过多年的探索和研究，多国科学家用各种方法做成功群速超光速实验和负群速实验，我们将其归结为以下几类：

①在短波和微波利用传输线的分段组合造成反常色散状态，从而获得超光速群速乃至负群速。例如，2002 年Hache[14]用多个同轴线段级联，获得vg/c=2～3.5；用类似方法，Munday[15]获得vg/c=4，以及vg/c=-1.2；2003年，黄志洵[16]获得vg/c=2.4；周渭[17]获得vg/c=2.2，以及vg/c=-1.45；另外，2012 年姚欣佑[18]用3 段矩形波导级联，模式效应和干涉效应造成群速超光速，vg/c=10。

值得一提的是，2014年笔者指导博士生姜荣在微波进行实验[19]，利用左手传输线（Left Hand Transmis‐sion Line，LHTL），在反常色散基础上又有负折射（n＜0），获得负群速，vg/c=-1.85。我们用数字示波器对输入波形和输出波形作比较，直观地看到了输出超前于输入的现象。

上述实验均在经典物理学框架内进行，没有量子理论与技术的介入。

②采用量子光学方法和技术，但仍要利用反常色散的状态。具体讲，利用电磁感应吸收（Electromagnetically Induced Absorption，EIA）媒质中的反常色散态；2000年Wang[20]在光频以激光脉冲通过铯原子气体，得到负群速vg=-c/310；2003年Stenner[21]以激光脉冲通过钾原子气体，得到负群速vg=-c/19.6；2006年Gehring[22]在光频用掺铒光纤放大器，由增益系统的反常色散，激光脉冲通过光纤获得负群速，得到vg=-c/4000。

③还是用量子光学方法，但技术上更复杂了。例如，利用电磁感应吸收（EIA）媒质中的反常色散态；2011 年Zhang[23]在光频运用激发光Brillouin 散射的非线性过程，又构建光纤环腔，激光脉冲通过光纤获得超光速群速及负群速；又观察到输出信号对输入信号超前，得到负群时延τg=-221.2ns；2012年Glaser[24]在光频以激光脉冲通过铷气室，又用4波混频技术，获得负群速vg=-c/880。

④还是使用经典物理的方法和技术，但引入某种特殊的电磁状态。例如，利用电磁器件中的消失态；1992 年Enders[25]在微波使脉冲通过处于消失态的截止波导管时，发现群速超光速，vg=4.7c；1997 年Nimtz[26]用相同方法获得vg=4.34c；1999 年Wynne[10]用类似方法获得群时延τg=-110fs。

以上实验涵盖了短波、微波、可见光这3 个频段，技术上既有经典的也有量子的，方法上有较简单的和非常复杂的。这些工作的成就和意义不容否定。

6 近区场电磁现象的新理论

本文在开始时就提到，一个电磁波辐射源(例如天线)的外部，随距离而区分为近区和远区。实际上，在两者之间有一个过渡性的中区。近年来的研究表明，近区场和中区场的动力学比远区复杂许多，且有几个特殊性质陆续被发现出来，主要有4个方面：

——静态性，亦即与静态场（例如静电场）相似的特性；

——消失态性，即与消失场相似的特性[27]，例如几乎纯电抗性的特征，以及场强随距离加大的迅速下降；

——超光速性，即其传播速度可能比光速大；

——负速度性，即可能出现负波速，以及在时间上的反向运动，实际上是出现超前波。

为什么近场与远场如此不同? 为何它具有这些奇怪的特性? 我们尚不能完全解释，只能有待今后认识的深入。

式中G为Newton引力常数：

自ISL 提出后的300 多年来，还没有哪个理论在预言的精度上可与之相比。

如果我们注意到半径为r的球的面积计算公式为

则容易理解平方反比规律为何出现在不同的物理现象中。ISL 是在1687 年由I.Newton 提出的；在ISL 出现98 年后，即1785 年，法国物理学家C. Cou‐lomb 宣布，他通过实验发现：带同号静电的两球间的斥力与两球中心间距的平方成反比，与各自所带电荷乘积成正比，即

这是Coulomb 定律，它与万有引力定律惊人地相似，这就启发人们做进一步的比较研究。实际上，Coulomb 定律也是ISL。假设引力传播速度是超光速的，Coulomb 场（静电场）传播速度是否也比光速快？这是有可能的，国际上也循此途径开展研究，有关成果反过来又会促进对引力传播速度研究。

2000 年，墨西哥物理学家R.Tzontchev[28]使用van de Graaf 静电发生器开展研究。两金属球半径10cm，中心间距3m，离地面高度1.7m。使用了尖锐的电脉冲。测量结果是，Coulomb 作用的传播速度为v=（3.03±0.07）×108m/s，亦即v=1.0107c，比光速快了1.07%。

R.Sminov-Rueda是西班牙物理学家，2007年他指导完成两篇论文，其一为A.Kholmetskii[29]的文章“束缚性磁场推迟条件的实验”，此文用环天线做研究，进行了实验，获得两个超光速数据（v=2c，v=10c）。对此的解释是“近区束缚场的非局域性质”（nonlocal prop‐erties of bound fields in near zone）。我们知道，非局域性（Non-Locality）是量子力学（Quantum Mechanics，QM）的重要特性之一，其含义几乎等同于超光速性（Super Luminality）。因而，这篇论文的观点是意味深长的：要用量子理论来研究近区场。

A.Kholmetskii[30]的另一文章是“近区束缚电磁场传播速度测量”，理论分析计算和实验都更完整。发送、接收天线均为环天线，安装在尺寸大于3m 的木桌上。实验给出了v/c与r的关系；在远区（r≥80 cm），v=c；在近区，当r=（50～60）cm，v=4.3c；当r=40cm，v≅8.2c。结论是，当r＜λ/2π，束缚场以超光速传播，表现出明显的非局域性。

2011 年O.Missevitch[31]的论文似为Smirnov-Rueda 指导下完成的第3 篇对的研究，实验技术和方法均有改进。文章给出的一个测量结果是v=（1.6±0.05）c；作者们认为有关工作属于“超光速的电磁波传播物理学”（Physics of EM wave propagation at a speed exceedingc）。

2014 年R.Sangro[32]的论文“Coulomb 场传播速度的测量”，竟然是从讨论引力传播速度问题开始的。这证明我们的判断正确，即宇宙中的具有相似的规律，对它们可作有益的比较研究。作为源的东西并非仅为孤立的电荷，而可以是作匀速运动的电子束，亦即以恒定速度移动的电荷，其产生的电场仍是Coulomb 场。实验技术复杂而精细，结果中未提供明确的速度数据，但证实了“电子束携带Coulomb场”的想法。

以上文献在时间上涵盖了2004 年至2014 年，获得的Coulomb 场传播速度处在超光速即（1.01～10）c的范围内。有关进展不仅丰富了对近区场的认识，还使我们坚定了“引力以超光速传播”的信心。

现在我们讨论一个重要的理论问题——近区场的“类消失态”性质。电磁波的时间相位因子是ejωt-γz，其中z是传播方向的坐标（距离），γ是传播常数（γ=α+jβ，α衰减常数，β相位常数）。对于金属壁均匀柱波导而言，内部电磁状态是有截止现象的场，截止频率ωc=2πfc（下标c代表cutoff）。可以证明与fc对应的截止波长为

式中h是本征值（Eigen Value），不是Planck 常数。上式体现了非零本征值的传输系统的特性。

现定义一个参数叫传播因子（Propagation Fac‐tor）：

因而传输系统可分为两区域，即传输区和截止区；由于截止区kz几乎是纯虚数，对应的波矢称为虚波矢（Imaginary Wave Vector），相应的波叫虚电磁波（Imaginary Waves）。现在我们可以对波导内的两种电磁状态作比较：

①传输区（传输态）：f＞fc，α很小，β较大，传播常数（近似值）γ≅ jβ，传播因子（近似值）kz≅β；

②截止区（消失态）：f＜fc，α很大，β很小，传播常数（近似值）γ≅α，传播因子（近似值）kz= - jα。

不仅如此，两者均随距离增大而迅速衰减，只是下降规律不同——消失场按e-αr规律，近区场按与r3（或r2）呈反比关系的规律。我们认为在一定条件下两者可以非常接近；取消失场强为

电小天线的场强为

现在令Ee=| |ES，即

等式两边各取自然对数，得

故可得

只要上式满足，两种场的下降完全一样。这虽在实际上不太可能（因上式中a与r有关），但却是两个随r增大而不断减弱的场的有趣比较。

Budko 认为存在一个区域，在其中波形主体随时间作逆向运动——随着离源的距离加大，接收者收到的波形极值的时间不断提前。假设源为有限正弦波束，中心频率f0=4GHz，这时r=10～100mm 为近场、中场区域，对近的模拟计算表明，在近场区（例如10～13.6mm）亦即outer edges shift right‐wards（正常现象），而inner part shift leftwards注意这与环境无关，即使在真空中也是如此。

现在我们尝试用量子理论解释近区场超光速现象。2007年Kholmetskii[29]等声称，他们在天线近场实验中“证实了非局域性”，因此对这个Non-Locality 应有更深刻的了解。笔者认为量子力学（QM）的3 个本质特征中其近场实验对非局域性的肯定表示

1971 年C.Carniglia[34]发表论文“电磁消失波的量子化”，文中“选择利用消失波的虚光子途径来表达场”。1973 年S.Ali[35]发表论文“量子电动力学（Quan‐tum Electrodynamics，QED）中的消失波”，文中说“消失波实际上是承载场和源相互作用的虚光子”，又说消失波将成为一个量化理论的虚粒子群；消失场与虚光子场是相同的，这并不是一种模式对模式的同一性。2006 年A.Stahlhofen[36]发表论文“消失模是虚粒子群”，文中说多年来基于QED 的研究认同消失模与虚光子的一致性，其怪异性质（如非局域性和不可观测性）违反了相对论因果律。2000 年G.Nimtz 教授曾致函笔者说“只有在引入并考虑QM 时，消失模才能得到正确描述和理解；消失模现身为虚光子，但它不能测出”。他又说：“我认为消失模是满足Galilei不变性的”。

因此，从量子场论（Quantum Field Theory，QFT）和量子电动力学（QED）的角度看，消失态是虚光子群总体贡献的结果。既然电磁源近场的两个组成部分（束缚场和消失场）是类消失态和消失态，故用虚光子理论作为超近区的超光速现象的解释是有益的。例如Nimtz曾指出，在Feynman型时空图上，虚光子对应的过程是空间距离在变而时间基本不变，这就代表有潜在的极高速度。这使笔者感到，用经典电磁理论研究截止波导时，发现在截止区相位常数近于零[8]，这都是指出消失态传播非常之快的状况。

总之，我们可以想象一下，一个被纯电抗性场紧紧包围的源天线，有功功率（有时是强大的有功功率）却从这种贮能场环境中冲出，在远区形成接近平面波的电磁结构，这是非常生动有趣的场景。近年来在非常靠近源的地方发现了超光速传播现象和负波速传播现象，这都要求更深刻的解释。而把上述现象与纯粹Coulomb 场、以及充塞宇宙中的引力场的超光速传播现象相联系，这种比较研究给人们带来了更多的启示。

本文给出了多个理论上的对偶关系——束缚场与消失场；推迟解与超前解；正波速超光速与负波速；静态电磁场传播与引力场传播；经典电磁学分析与量子理论分析；实光子与虚光子。这些对偶性质的二元化特征正是事物本性的体现。

7 Einstein 的负速度理念及Brillouin 负群速理论的实证

现在我们将把讨论引向深入，首先回顾负速度概念的早期情况。20世纪之初，A.Einstein[37]创立了狭义相对论（Special Relativity，SR），在此期间他考虑过负速度的事情。Einstein 认为，需要确定物理作用速度（Velocity of Physical Action）和信号速度（Velocity of Signal）是否能超过光速，对此他表现出犹豫不决的心理。1907年Einstein[2]发表的文章“关于相对性原理及由此得出的结论”，其中§5（“速度的加法定理”）的内容既与信号速度有关，又与负速度有关。文章说，假定沿参照系S的x轴放一长条物体（图2），相对于它可以用速度u传递某种作用（从长条物体来判断），并且不仅在x轴上的点x=0（点A），而且在点x（点B）上都有对S静止的观察者；在A处的人

图2 Einstein讨论信号速度时所用的图形

，通过长条物体传给在B处的人，长条物体以速度v（＜c）沿（-x）方向运动。那么，根据SR速度合成公式，信号速度为

传递时间为

其中，l为物体长度。如u＞c，则选择v（＜c），总能使ts＜0。这就出现了负的传递时间，以及负的信号速度。Einstein 认为，这种传递机制造成“结果比原因先到达”，因此“不可能有这样的信号传递，其速度大于真空中光速”。

对他的这种说法，笔者认为是不合适的。由于我们已经对SR 理论作过深入分析和严格批评[38]，这里不再讨论SR 本身，也不再评论Einstein 的加法公式，只作简单的探讨。有趣的是，Einstein 虽然作出了“信号速度不能超光速”的基本判断，但又不做百分之百的肯定。他说：“虽然这种结局单从逻辑上考虑可以接受，并不包含矛盾；但它同我们全部经验的特性是那么格格不入，所以u＞c假设的不可能性看来是足够充分地证实了的。”在这里，Einstein 表示违反因果性的事可以不违反逻辑，只是由于它违反人类经验，所以信号速度不可能超光速。

1914年，A.Sommerfeld[3]及L.Brillouin[39]建立了经典波速理论，虽不理想但其价值远胜于Einstein 的工作。如所周知，波速有两种不同概念——相速vp和群速vg，通常认为群速的意义大于相速。至于对群速的评价，存在两种不同的倾向——估计过高与估计过低。前者的例子是英国的物理学家Lord Rayleigh，1877 年在其著作《Theory of Sound》中不仅定义了群速，还认为群速与能量速度、信号速度一致；但我们现在知道这个观点只在一定条件下才正确。也有别的人认为群速极其重要。另一种观点则对群速的估计十分低，似乎对它的研究（无论计算或实验）不具有价值和意义。笔者对这两种倾向都不认同。如果不研究群速，用什么来代替呢？在许多情况下，能速、信号速都十分复杂，实际上难以掌握。波前速度（Front Velocity），在SB 理论中被认为是一种突然性扰动的传播速度，其定义欠明确。可以说，在讨论电磁波（或说电磁信号）的速度问题时，群速仍然具有基础性和重要性，可作为科学研究中有参考价值的资料。如果在实验中采取复形（Reshape）措施，以减小波形失真或做到完全不失真，那么情况就更好了。

1914 年A.Sommerfeld[3]详细讨论了波速度问题。他假定t=0 时在媒质表面（z=0 处）突然出现一个正弦波f（0，0），位于z处的观察者要在t=z/c时才能看到有瞬态现象发生。从此时起直到稳态信号建立，这个过程中才有信息传递。Sommerfeld 在复频域（p=σ+jω）研究，以f（0，0）为入射波，他导出以下述积分方程描写在z处的波

式中实数σ要保证积分路径在一定区域内，ω0是稳态载频。上式也写作

实际上直到t=z/c，才有波前（波阵）到达，波前速度是c；当t=z/c，稳态、瞬态分量抵消，波仍为零。这表示信号总是从零起逐步建立。t＞z/c，就有

α、β分别为媒质的衰减常数、相位常数。在稳态完全建立之前的过程，则称为预现波（Precusors），也叫前兆——它逐渐而迅速地发展，完成一个连续的过渡。

为了了解信号建立的全过程，必须对上述积分方程求解。同样是在1914年，L.Brillouin[39]用鞍点积分法求解Sommerfeld的积分方程。经过复杂的演算和在复平面上的作图分析，他得到了一个曲线族。图3是1960年Brillouin[4]根据积分方程给出的vp和vg与频率的关系（注意纵坐标是光速c与波速v的比值，即c/v），显示出在整个频域，总有vp＞c。但c/vp可能大于1（vp＜c），也可能小于1，即存在vp＞c；这些结果是对的。但Brillouin排除负相速的可能，这个结果并不正确。Brillouin对群速的规律描述更有意义，由图3可见：既有vg＜c的情况，又有vg＞c的情况。不仅如此在中心频率附近，会出现3 种现象，即群速超光速（vg＞c），群速无限大（c/vg=0），负群速（vg＜0）。必须注意，群速不断增大，直到，才达到负群速。这些分析结果已被许多事实所证明。

图3 Brillouin理论中的相速和群速

今天我们如何看待Sommerfeld-Brillouin 波速理论？对它全盘肯定或全盘否定都是不对的。笔者指出它有下述问题[12]：①该理论排除了出现负相速（因而出现负折射率）的可能，与目前已知的理论和实验研究结果不符；②该理论虽指出了出现负群速的可能，但却不能阐明其物理机制和意义；③该理论研究信号速度的方式，理想的阶跃函数要求无限大带宽，在实际中无法实现，使人怀疑定义方法及研究方法是否存在问题，亦即该理论并未构造出一个合理的信号速度定义；④由于SB 理论出现在量子力学发明之前多年，因而前者不可能估计到量子势垒受粒子影响从隧道穿越时的超光速现象；⑤该理论对波前速度缺乏严格的定义。……不过，SB 理论对今天的研究人员仍有一定参考价值。

必须注意，图3 的纵坐标是c/v，即c/vp或c/vg；因此，代表群速的曲线通过c/vg=0 的那一点，表示群速达到无限大。因此，Brillouin图的特点是，它描写了群速不断增大时，只有越过无限大，才达到负群速。这就是说，NGV 代表一种比这似乎难以理解，但并不特别令人惊奇。2021 年，笔者在一篇论文中根据Casimir 效应描绘了一种“比自由真空还要空的”[40]，就是一种类似的情况。你可以怀疑：怎么会有比无限大速度还快的速度?! 也可以怀疑“怎么会有比真空还空的真空?!”但自然科学研究已进入了这样的阶段，即人们不得不承认一些难于理解的事情，只要它有实在的理论证明或实验证据。

S.Chu[13]发表论文“吸收媒质中的线性脉冲传播”，似为用实验证明NGV存在的第一人，是负速度在实验上取得突破。Chu仿照Ulbrich的方法，试样为外延生长的GaP/N，厚度为76μm或9.5μm；令厚度为L，则有

故测出τg即可计算出vg，而试样从光路中接入和取出是实验步骤。显然，如测到了零时延（τg=0），就是测到了无限大群速（vg=∞）。图4 是取L=9.5μm 时的实验结果。可以看出三方面（vg＞0,vg=∞,vg＜0），而且过渡是平滑的。在这里我们要强调指出，这条实验曲线与多年前Brillouin 的理论计算曲线（Brillouin图中的群速曲线）是十分相似的!

图4 最早的NGV实验结果(Chu, 1982)

8 超前波是具有负速度的波

虽然Chu[13]和Wang[20]都测出了NGV，但前者是用经典物理学方法，后者是用量子光学方法。有趣的是，Wang 的论文在名刊《Nature》上发表后，由于该文自称是一个“超光速实验”，引起某些相对论者不满。例如文献[42]对Wang 的论文及造成的影响进行猛烈的批判。但是，文献[42]的作者虽然熟悉相对论，但对Born 和Wolf 所论述的“波速是标量而非矢量”却不知道，对Sommerfeld-Brillouin 波速理论也一无所知，因而作出了错误的评判。文献[42]说，Wang的实验结果是（vg=-c/310），取绝对值后得到c/310，因而是亚光速。这种说法完全不对；Wang 的实验结果是-c/310，不是c/310，这两者存在根本上的不同。

不仅知此，虽然文献[42]的作者是崇拜Einstein的，但对其1907 年论文的论述也是一无所知。回顾1907年Einstein[2]的讨论，负的传递时间与负信号速度同时出现是其特点；而且这种讨论表明负速度是超光速的特征之一，因而Einstein是为了论证“超光速不存在”才否定了负速度的意义。可见，关键在实验，如果实验上证明（不仅仅是WKD 实验[34]，还有近年来更多的实验）了负速度存在，那就表明超光速是存在的。这也就是Wang坚持他的实验是一个超光速实验的原因。因此文献[42]的主要论点不能成立。更何况，把负速度的“负”简单地看成“反方向”是不对的，因为波速更应看成标量而非矢量。

文献[42]也有可取之处；首先，它指出，在研究超光速问题时常要与负能量概念相联系。该文说：“光脉冲以（-c/310）从出口处向入口处移动，这符合我们对负能量密度移动速度的计算；负能密度不好解释，‘负’或许表示从铯原子气体中提取能量。”

其次，在“SR 不允许超光速”这个相对论命题上，文献[42]作了理论上的“让步”。该文说：“SR 未排除光在其他物质作用下不会运动得比c更快，关键是用固有时判断因果次序，这样如在其惯性系满足因果律则在一切惯性系中都会满足因果律；修改Einstein 对因果律解释后允许这种超光速存在。”

但是，这种论述仍然是把“因果律”绝对化，当作不能违反的“铁律”。由于具有负速度的波就是超前波，因此对这种波而言也是违反经典因果律的。我们再次强调指出，超前波的单独存在是可能的，这已为众多NGV 实验和近区场实验所证实。笔者认为，用时空图描写负波速现象可以帮助理解。例如对Wang[20]的实验，可以用图5 来描述。其中L是气室厚度。这个图也可用于说明Chu[13]的实验，L则为样品厚度。

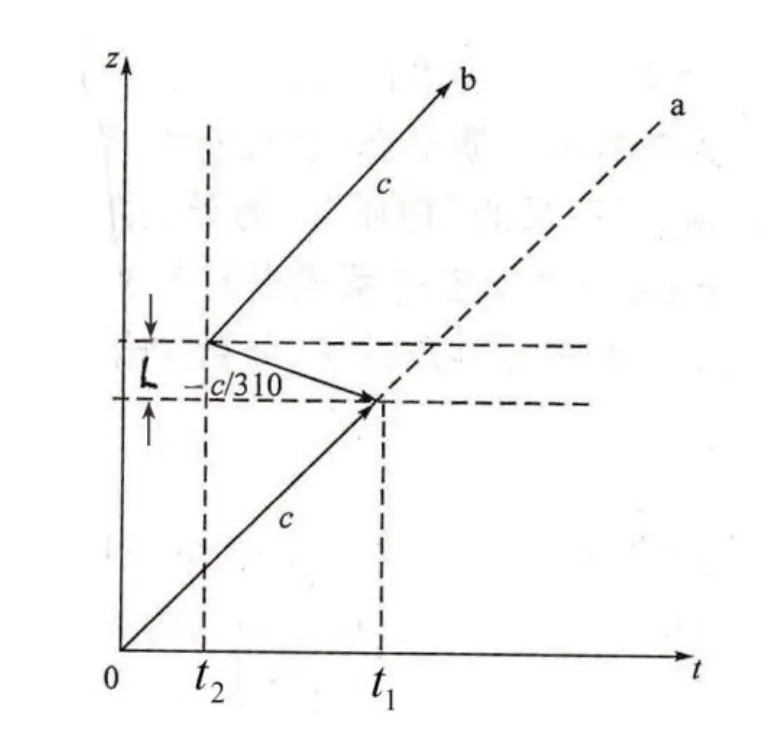
图5 表示负速度的时空图

图5的横坐标是时间（t），纵坐标是距离（z），t=0是光脉冲运动的出发时间。在0～t1这个时间间隔，脉冲在真空中以光速（c）运动。当t=t1，光脉冲进入气室，群速成为负值（vg=-c/310）。当t=t2，光脉冲在出口处现身，但t2＜t1，亦即t2-t1＜0（负时间）。从t2开始，光脉冲继续以光速c向前运动，展示在图的高处。……这个图有一定价值，但在实际分析时会更复杂，涉及对光脉冲宽度的考虑，此处从略。

（下期待续）