基于二阶差分MFCC深度学习的声景基调声分类方法

邓志勇, 张万亿, 刘爱利

（1.首都师范大学音乐学院，北京 100048；2.中央音乐学院音乐人工智能与音乐信息科技系，北京 100031；3.首都师范大学资源环境与旅游学院，北京 100048）

1 引言

“声音景观（Soundscape）”，即声景，较早由芬兰社会学与地理学家格兰诺（Johannes Gabriel Granö）在1929 年提出，其中心思想是“研究以听者为中心的声音环境”[1]。之后在20 世纪六七十代，由加拿大作曲家与生态学家谢弗（R. Murray Schafer）与托阿克斯（Barry Truax）等系统地构建了声景学的理论与方法论框架，认为声景是一种“强调个体或社会感知和理解方式的声音生态”[2]。声景思想提出的初衷是培养人们聆听与改善声音环境的能力，“人-声-境（Human-Sound-Context）”是声景的三个基本层次[3]。2014 年，国际标准化组织（ISO）将声景定义为“在某种场境下，由个人或群体感知、经历和（或）理解的声学环境”[4]。

越来越多的音频分类算法结合了不同的特征，例如隐马尔可夫模型、支持向量机、高斯混合模型[5]和本文将使用的卷积神经网络[6]。然而，与语音等音频信号相比，声景样本分类任务具有其特殊性，因为它们具有更广泛的能量频率分布，并且包含更多丰富的人与环境信息，使得其比语音信号更为复杂[7]。基于“人-声-境”的相互关系，谢弗认为声景可分为基调声（Keynote）、信号声（Signal）和坐标声（Soundmark）三种基本类型，指出人们“通常不会有意识的感知基调声”，信号声“与基调声形成对比”，而坐标声是“引起特别考虑与注意的声音”[8]。基于上述观点，本文对声景样本进行分类时，在总体上将声景进一步划分为“基调声（Keynote）”与“非基调声（Non-Keynote）”两个相互正交的类型，如表1所示。

表1 基于谢弗声景类型的基调声与非基调声二分类

在单个既定的声景样本中，相对于非基调声，基调声往往作为一种声压级动态较小、频率分布较广、时域变化较小的稳态背景声出现，主观听感也相对稳定[9]。例如，图1 和图2 分别为样本No.71 中的长时稳态基调声（于北京景山录制，包含了自然声和游客的喧闹声）和样本No.115 中的短时瞬态非基调声（于北京鼓楼录制的击鼓表演时的击鼓声，具体样本编号所对应的区域如表2所示）的光谱图。两者对比可知，图1直观地显示出了典型基调声的稳态特性。

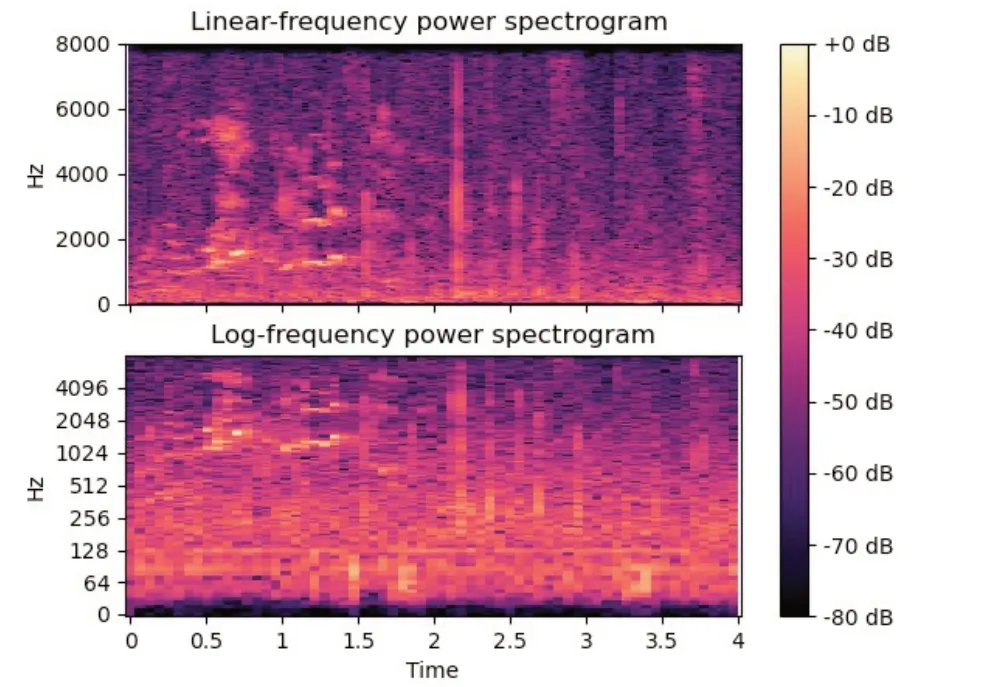
图1 样本No.71中基调声光谱图

图2 样本No.115中非基调声的光谱图

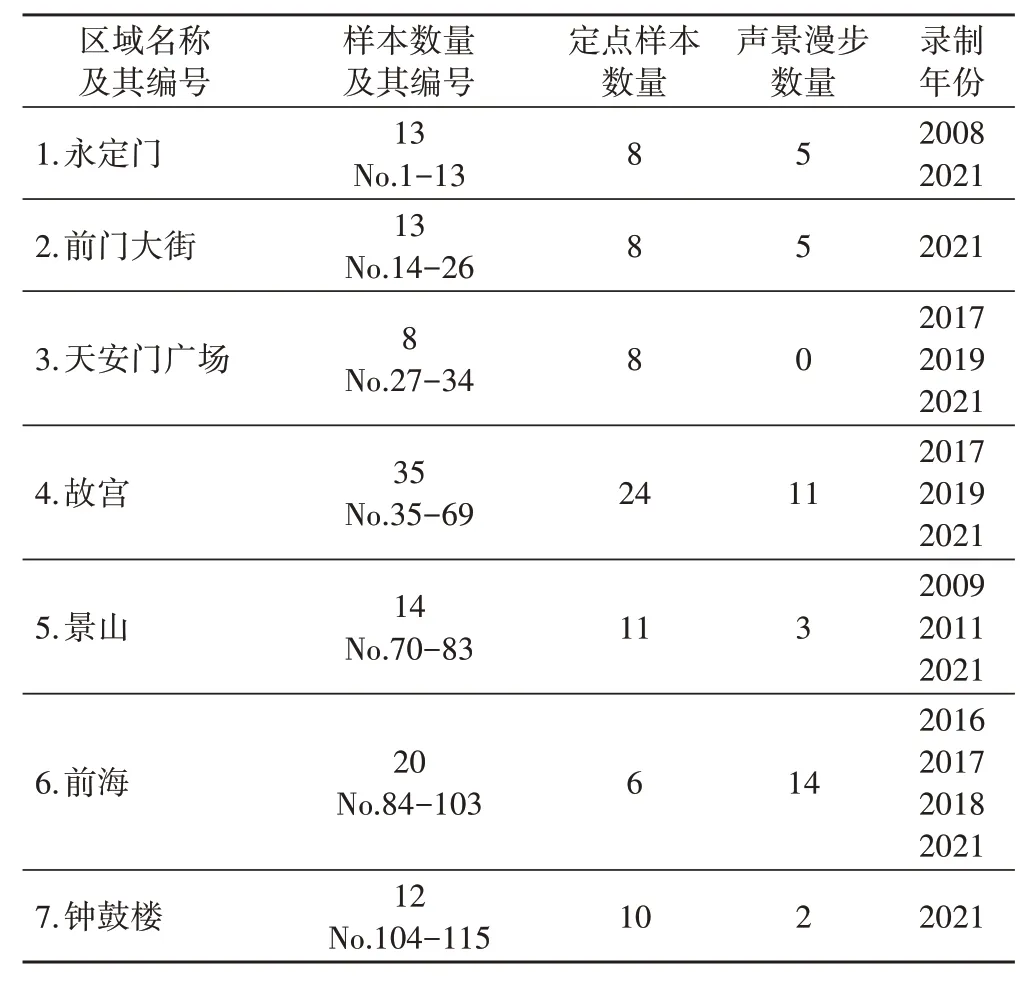
表2 老北京中轴线声景数据集的基本信息

因此，本文在与传统音频分类方法中所采用的均方根包络（Root Mean Square Envelope, RMS）、Mel 频谱、梅尔倒谱系数（Mel-frequency Cepstral Coeffi‐cients, MFCC）进行比较分析的基础上，尝试提出一种改进后的二阶差分39 维梅尔倒谱系数（以下简称“二阶差分MFCC”），以卷积神经网络（Convolutional Neural Network，CNN）对声景样本进行“基调声-非基调声”二分类，构建一个较为完整的深度学习网络模型，以适应此类注重主观听感选择并具有“人文色彩（Humanistic Color）”特征[10]的分类任务。

2 研究样本与方法

2.1 研究样本

本文研究所用的声景样本数据集覆盖了图3红色虚线框所覆盖的老北京中轴线的主要区域，从其南端的永定门至北端的钟鼓楼，总长度约为7.8公里，分为永定门、前门大街、天安门广场、故宫、景山、前海和钟鼓楼及其主要连接道路及周边等七个区域。所有声景样本均为WAV 格式，采样频率为48kHz，量化深度为24bit，由专业录音师佩戴Sennheiser Ambeo 录音耳机以符合国际标准化组织（ISO）技术标准的双耳全景声制式，以“定点录音（Location Recording）”和“声景漫步（Soundwalk）”两种方式进行录制[11-12]。具体各样本编号及其所对应的区域，以及各区域中以上两种录制方式的样本编号、数量和录制年份如表2所示。

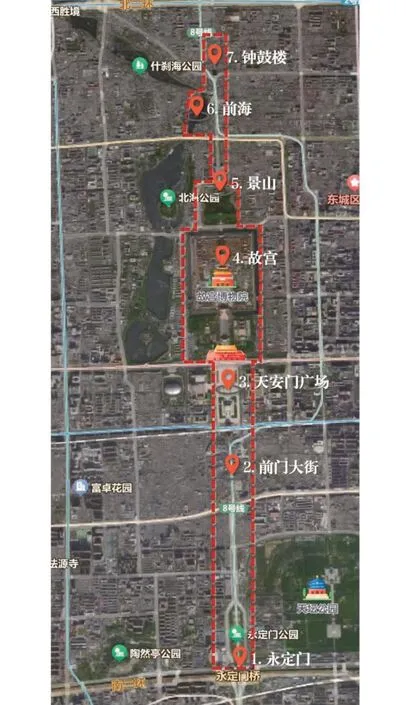
图3 老北京中轴线声景数据集分布的七个区域

老北京中轴线是一个功能多元、活动繁忙的城市综合区域，交通与人流量大，区域中众多的绿地、公园与知名景点吸引了大量游客与市民。绿地公园的自然声与城市交通噪声及嘈杂的人声不仅是其声景基调声的主要内容之一，同时也提供了大量的非基调声。老北京中轴线上时常会有一些传统音乐演出，如前门大街的叫卖吟唱，景山公园票友们的京戏演唱交流，前海火德真君庙的道教音乐表演，钟鼓楼的鼓乐队演出等，这些音乐声成为了具有“人文色彩”的非基调声。本文所选取的115个样本完整涵盖了图3所标注的老北京中轴线上的七个典型地理区域。这些内容丰富[13-14]的声景样本，在全面体现“基调声-非基调声”二分类的同时，也完整涵盖了声景学研究中常用的包括“自然声（Natural Sounds）”、“人声（Human Sounds）”、“社会声（Sounds and Society）”、“机械声（Mechanical Sounds）”、“安静与沉默（Quiet and Silence）”、“指示声（Sounds as Indicators）”等在内的六个基于内容划分的声音类型[8]。由这些样本所构成的声景数据库，充分满足了深度学习对样本多样性和典型性的要求。

2.2 数据预处理

根据深度学习模型的样本归一化要求，以表1的描述为标准，表2 中的115 个样本以“专家评分法（Expert Evaluation）”[15]进行人工分类标注，被分段截取划分为“基调声”与“非基调声”两个正交的层，形成1519个基调声段和1899个非基调声段。然后经过分层随机抽样，形成训练集的样本段总数为2394个，验证集的样本段总数为513个，测试集的样本段总数为511个。即从基调声段和非基调声段中分别随机抽取1453个和941个样本段，形成2394个训练集的样本段；从基调声段和非基调声段中分别随机抽取310个和203个样本段，形成513个验证集的样本段；从基调声段和非基调声段中分别随机抽取306个和205个样本段，形成511个测试集的样本段。最后由于CNN要求可处理的样本数据长度必须保持一致，因此每个样本段最终被划分为等时长的4秒片段，少于4秒的样本段将以零填充尾部至4秒[6]。

2.3 二阶差分MFCC特征的选取

一维时域的均方根振幅包络（RMS），类似频率非线性特征的Mel 频谱和如式（1）的从Mel 频谱中获取的带有高冗余信息的梅尔倒谱系数（MFCC）都是音频信号处理中常用的特征[16]。

其中，i为帧序数；n为列序数；m为Mel频率；H（i,m）为能量谱与Mel 滤波器转置矩阵的乘积；L为MFCC 的维数，本文中L=13；M为Mel滤波器的个数，本文中M=128。

如前所述，由于本文的分类任务具有“人文色彩”的特殊性，因此对式（1）的13 维MFCC 进行常规二阶差分运算，形成了冗余信息更为丰富的二阶差分39维MFCC（简称为二阶差分MFCC）作为本文的分类特征。图4显示了样本No.71中的基调声和样本No.115中的非基调声的RMS、Mel频谱和二阶差分MFCC 的谱图及其直观上的差异。

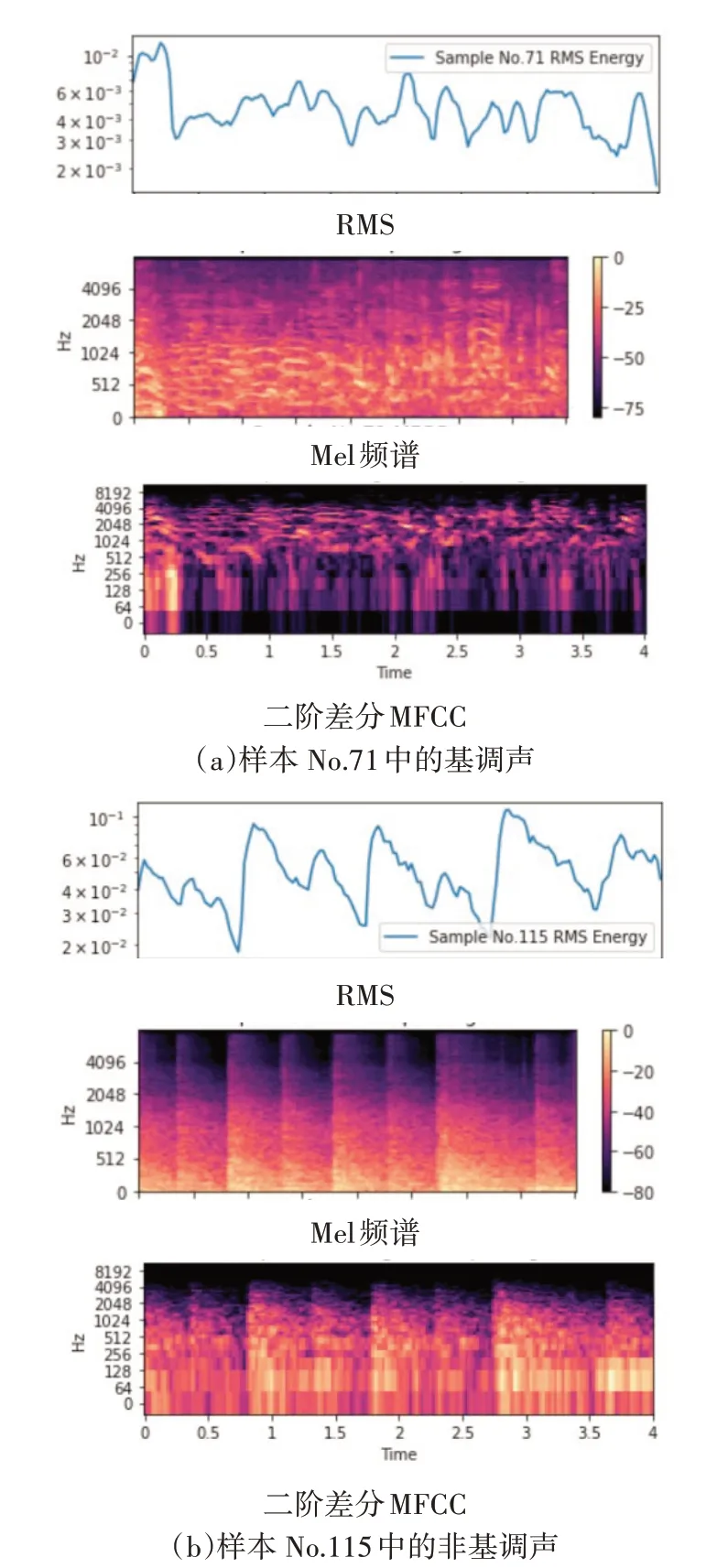
图4 样本No.71中的基调声与样本No.115中的非基调声的RMS、Mel频谱和二阶差分MFCC谱图

2.4 本文CNN结构

根据上节所选取的二阶差分MFCC 的分类，并便于与RMS和Mel频谱特征的分类结果进行比较，本文研究的技术路线如图5所示。

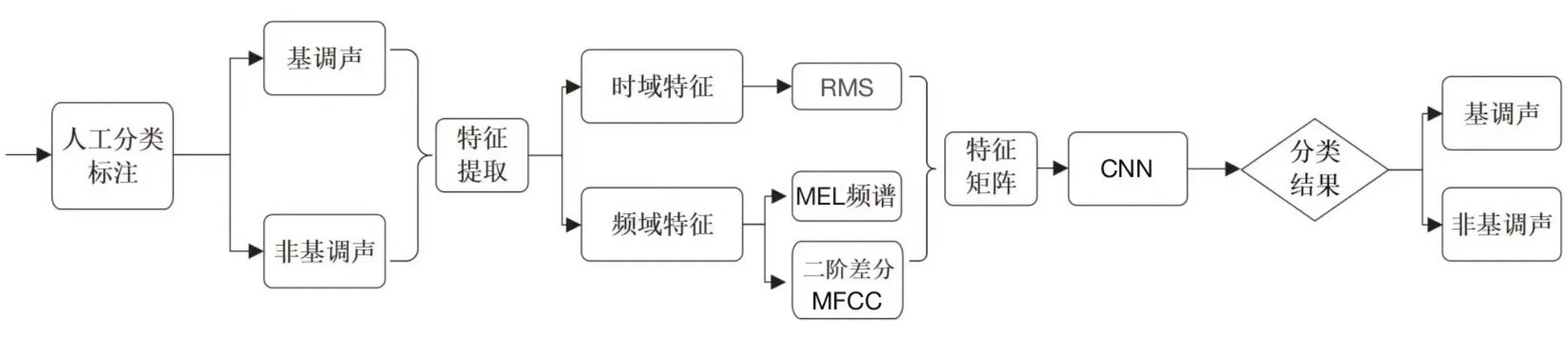
图5 研究路线图

在本文设计的分类器中，将基调声和非基调声称为“Class（类）”，每个经人工分类标注划分的样本段称为“Sample（样本）”，对应的类以“Label（标签）”进行标识，数值1表示该样本段为基调声，数值0表示该样本段为非基调声，标签经过“独热编码（one-hot cod‐ing）”进行预处理。由于所有深度学习系统中的基本数据结构都为以NumPy 数组形式存储的张量（Tenser），而神经网络的所有输入和目标必须以浮点型张量的形式呈现，且必须对数据进行向量化，因此本文将输入特征数据结构重构为一个包含数值的三维张量，设计的卷积神经网络结构如表3和图6所示。

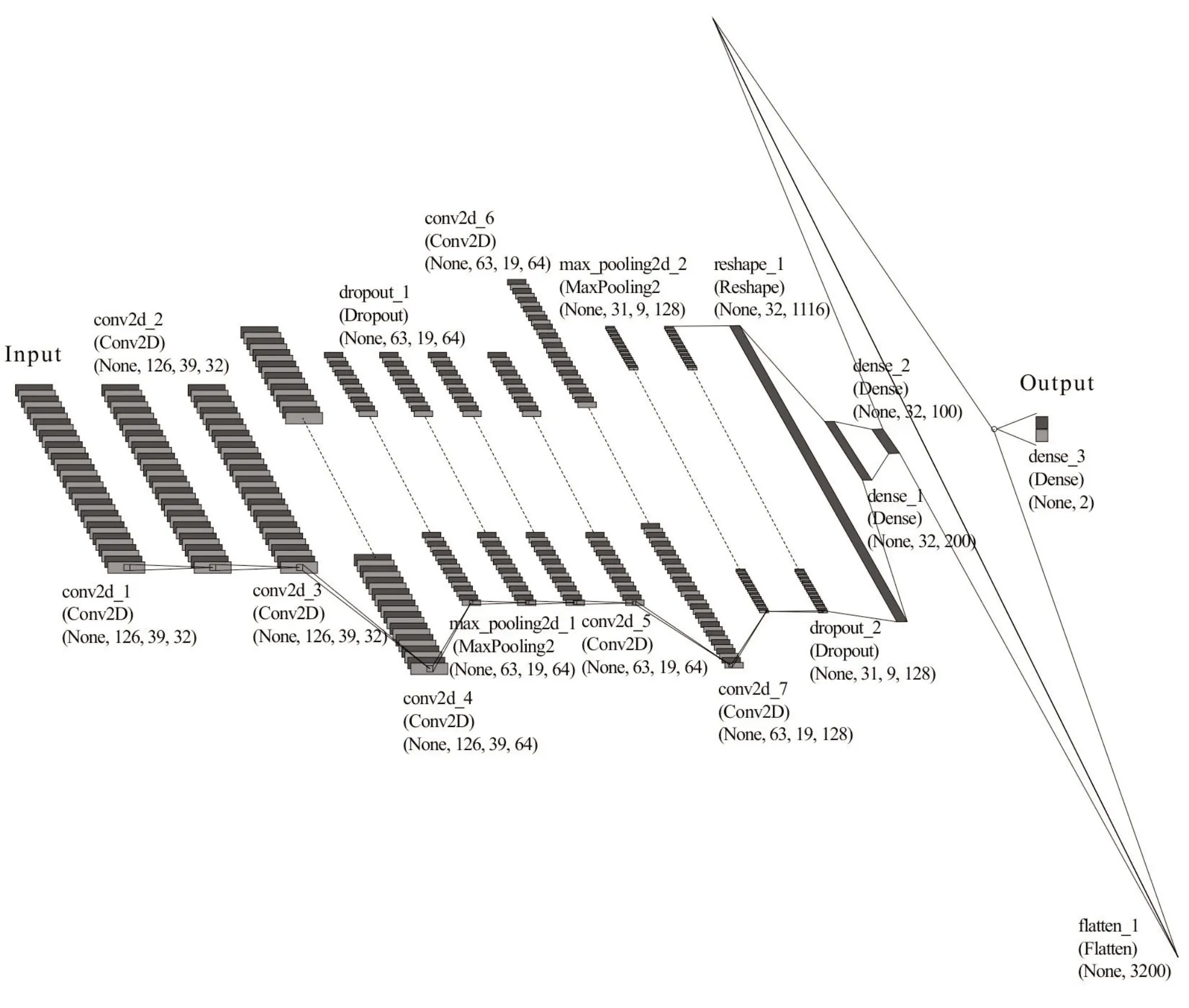
图6 卷积神经网络结构图

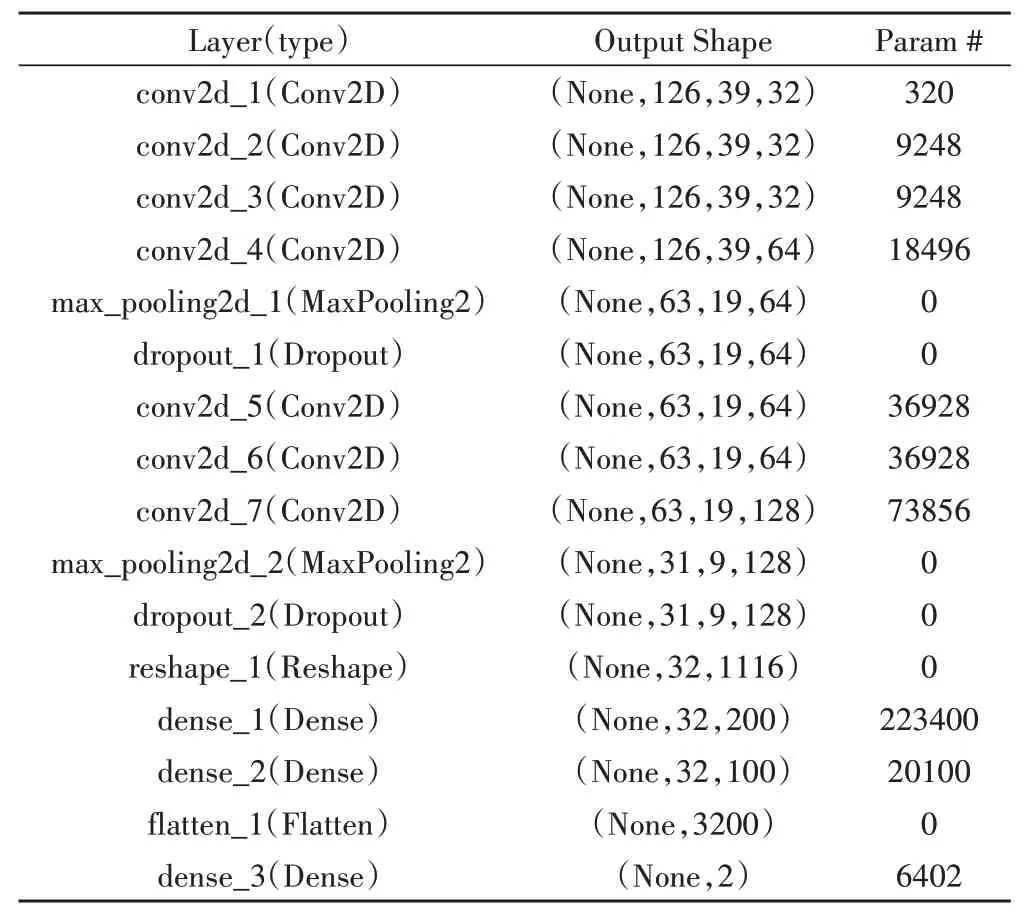
表3 本文卷积神经网络结构

在训练过程中，卷积核分别设置为32、64、128个，大小为3*3，将表3 中dropout 的值设为0.25。不同特征在CNN中具有不同的维度，如表4所示。整个深度学习过程在pytorch框架下实现[6]。

表4 特征阶数

2.5 中间层的激活函数与结果验证

由于本文以标签数值标量0和1进行二分类的标识，因此还将选择修正线性单元函数（ReLU函数）作为中间层的激活函数[6]，将上述网络神经元的输入层映射至输出层，以方便进行结果验证。该函数具有将所有负值返回为零的特性，可使网络稀疏，在一定程度上缓解了过拟合，对于二分类结果具有良好的验证性能。ReLU函数的表达式如式（2），图像如图7所示，经由该函数的神经元输入至输出的加权过程如式（3）所示：

图7 ReLU激活函数的图像

其中，b为偏置量，w1、w2、w3为加权系数。

3 分类结果

3.1 二分类训练的进度控制

表2 的数据集经预处理后，使用上述设计的分类器进行训练的部分进度控制如表5所示。

该表用于监控深度学习模型训练进度，其中“1372/2394”表示当前训练的“批次数/总批次数”，如在该例中，表示已经完成了1372 个批次的训练，总共需要训练2394 个批次。“ETA:33s”表示预计剩余完成训练所需要的时间，“Loss:0.6886”表示训练过程中的损失值，“acc:8.5598”则是以百分比表示的训练过程中的准确率。该表提供了当前深度学习模型训练的进度信息，包括已完成的批次数、训练进度的可视化、预计剩余时间、损失值和准确率等指标。通过观察这些指标，可以了解模型训练的进展情况和性能表现。

3.2 输出层的激活函数、损失函数、优化器与二分类识别准确率

为适应二分类任务的特点，本文接下来选择SoftMax函数[6]作为输出层的激活函数，其表达式如式（4）：

其中，ak为向量a的第k个分量。

如果输出神经元的数量为2，则SoftMax 函数具有一个属性，即输出值的总和为1，即满足约束条件：P（A|x）+P（B|x）=1。因此，可将SoftMax 函数作为一种基于概率统计的方法对目标进行分类。在本文中，输出越接近1，则识别结果与训练集中的基调声相似度越高，反之亦然。

此外，损失函数（Loss 函数）[6]是一种二元交叉熵函数，适用指示二分类问题中的分类误差，其表达式如式（5）：

其中，yi为分类标签：0为非基调声，1为基调声；p（y）为某一分类的概率值。

RMSprop 函数[6]则是本文选择的优化器，其表达式如式（6）：

其中，gt为时间步t的梯度；E[g2]t为时间步t的梯度平方的移动平均值；α是忘记因子，取值区间为[0,1)，常见值为0.9或 0.99；η0是全局学习率；ε为极小常数，以防止分母为零；Wt是时间步t的参数值。

最终，基于2.4 节的CNN 模型，分别使用RMS、Mel 频谱和二阶差分MFCC 三种特征进行训练的分类器，在测试集中获得的基调声分类识别准确率如表6 所示，三种特征的识别准确率曲线与损失率曲线分别如图8、图9与图10所示。

图8 使用RMS特征的识别准确率曲与损失率曲线

图9 使用Mel频谱特征的识别准确率曲与损失率曲线

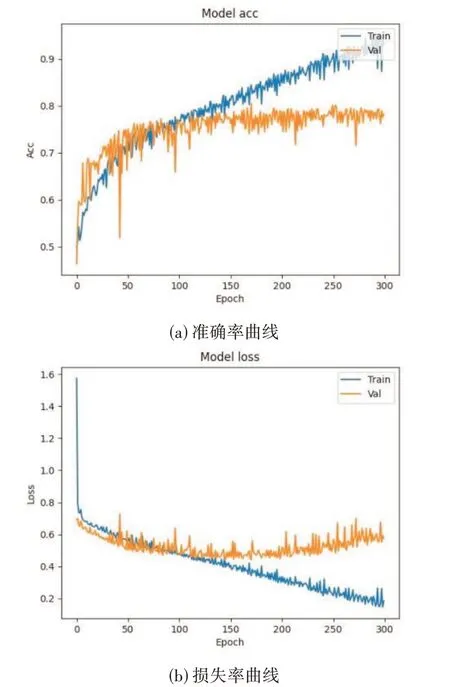
图10 使用二阶差分MFCC特征的识别准确率曲线与损失率曲线

表6 基调声识别准确率

由以上分析可知，使用RMS 特征的识别结果基本上相当于随机猜测，使用本文提出的二阶MFFC 特征的识别结果为80.23%，远高于使用传统Mel频谱特征68.68%的识别结果。

4 评价

4.1 性能评价

本文采用混淆矩阵（Confusion Matrix）[6]对上述分类结果进行性能评价。混淆矩阵为一个两行两列矩阵，每一列的数值表示所识别类别中样本段的数量，每列总和为所识别类别中的样本段总数，每一行则表示样本段的真实属性类别，每行总和则为该类别的样本段总数。因此，混淆矩阵由以下四个指标组成：

·TP（True Positive），真正例：模型将样本识别为基调声的真实基调声类别样本段数量。

·FN（False Negative），误负例：模型将真实基调声类别样本识别为非基调声的样本段数量。

·FP（False Positive），误正例：模型将真实非基调声类别样本识别为基调声的样本段数量。

·TN（True Negative），真负例：模型将样本识别为非基调声的真实非基调声类别样本段数量。

分别使用RMS、Mel 频谱和二阶差分MFCC 三种特征进行训练的分类器混淆矩阵分别如图11、图12和图13所示。

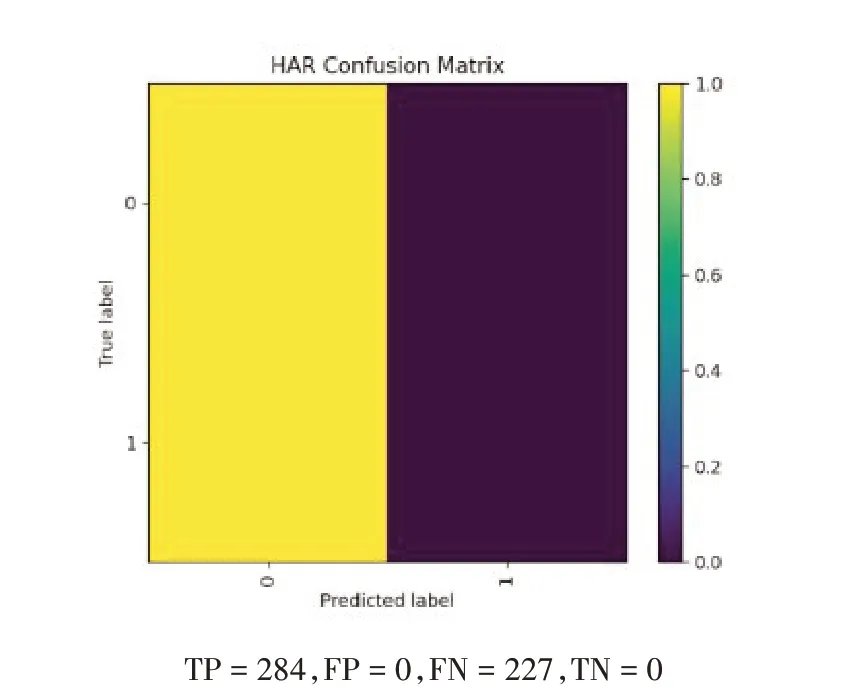
图11 使用RMS特征的混淆矩阵

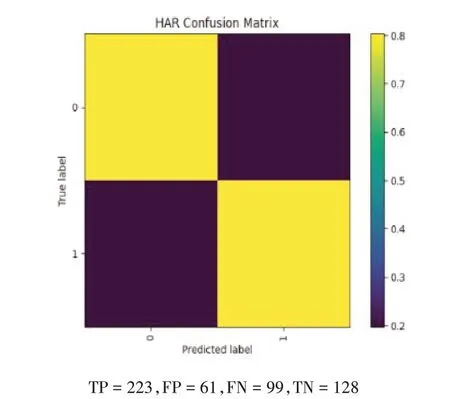
图12 使用Mel频谱的混淆矩阵

图13 使用二阶差分MFCC的混淆矩阵

可由TP、TN、FP 和FN 计算出其他四个更为直观的指标来评价二分类模型的性能，如表7所示。 四个指标的定义如下：

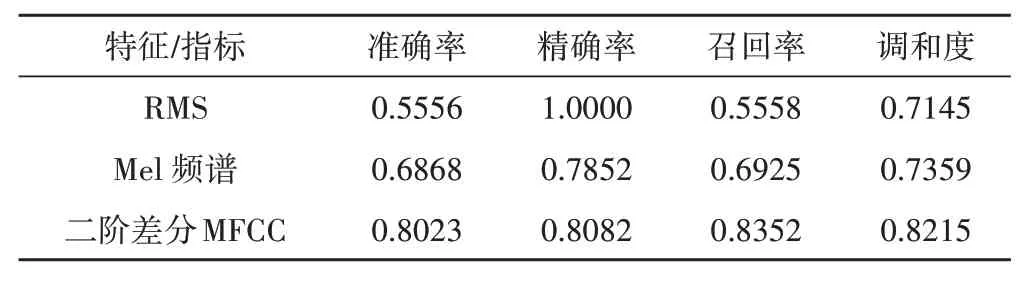
表7 三种特征进行训练的分类器性能

准确率：Accuracy=（TP+TN）/（TP+TN+FP+FN），即模型正确识别的样本数量占总样本数量的比例。

精确率：Precision=TP/（TP+FP），即模型被正确识别为正样本的数量与实际正样本数量的比例。

召回率：Recall=TP/（TP+FN），即正确识别的样本数量在实际样本数量中所占的比例。

调和度：F1=2*Precision*Recall/（Precision+Re‐call），为Precision和Recall的调和平均数。

4.2 识别能力评价

为了评价分类器识别能力的强弱，需要根据混淆矩阵计算另一个指标ROC 曲线[6]。这一曲线的横轴为误正率（False Positive Rate, FPR），即4.1 节中误正例FP 的占比，是在二元分类中所有实际负例中被错判为正例的比值；纵轴为真正率（True Positive Rate,TPR），即表6 中的召回率。ROC 曲线远离对角线，越趋近于坐标（0，1）时，则分类器模型的整体识别能力越强；ROC曲线越接近于对角线时，识别能力越弱；当ROC曲线为对角线时，则该二分类器模型为无效的随机猜测。参数AUC 则表示曲线下的面积：当AUC=1时，是理想的二分类器模型；当AUC=0.5时，则该二分类器模型为无效的随机猜测。AUC 值越接近1，则模型的整体识别能力越强。分别使用RMS、Mel频谱和二阶差分MFCC 三种特征进行训练的分类器的ROC曲线分别如图14、图15和图16所示。

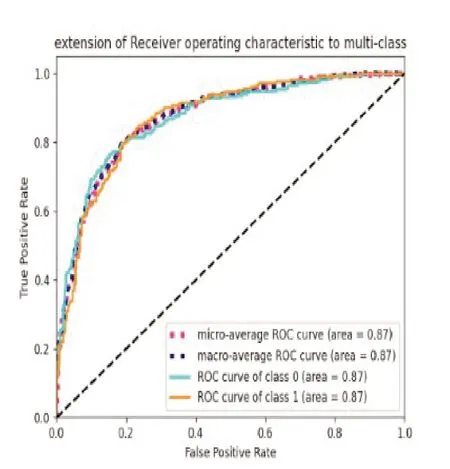
图16 使用二阶差分MFCC的ROC曲线

由ROC 曲线可知，RMS 的识别能力最弱，接近随机猜测，而本文提出的二阶差分MFCC 的识别能力最强。这可能再次表明，像RMS 这样的一维时域特征不适用于CNN网络的深度学习模型。不过ROC曲线通常对表示正负样本比例的大幅变化不敏感，因此在本文中，还采用测试数据的得分作为ROC 的阈值，以表6 中的召回率（Recall）作为横坐标，精确率（Preci‐sion）作为纵坐标，生成PR 曲线来评价模型的大幅变化特征，分别如图17、图18和图19所示。

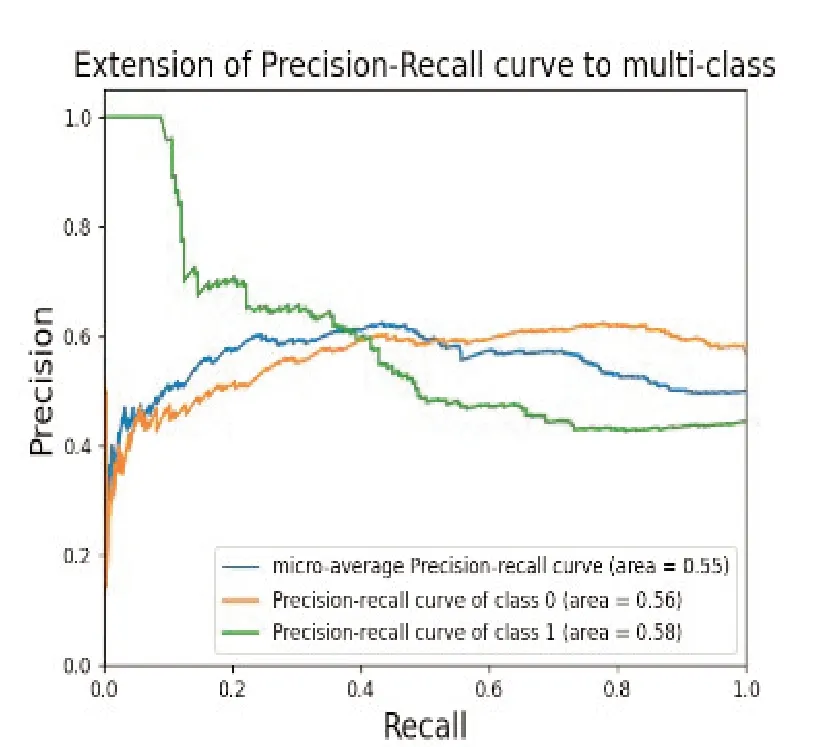
图17 使用RMS特征的PR曲线

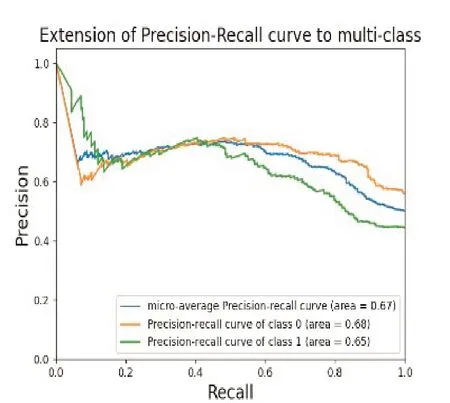
图18 使用Mel频谱的PR曲线

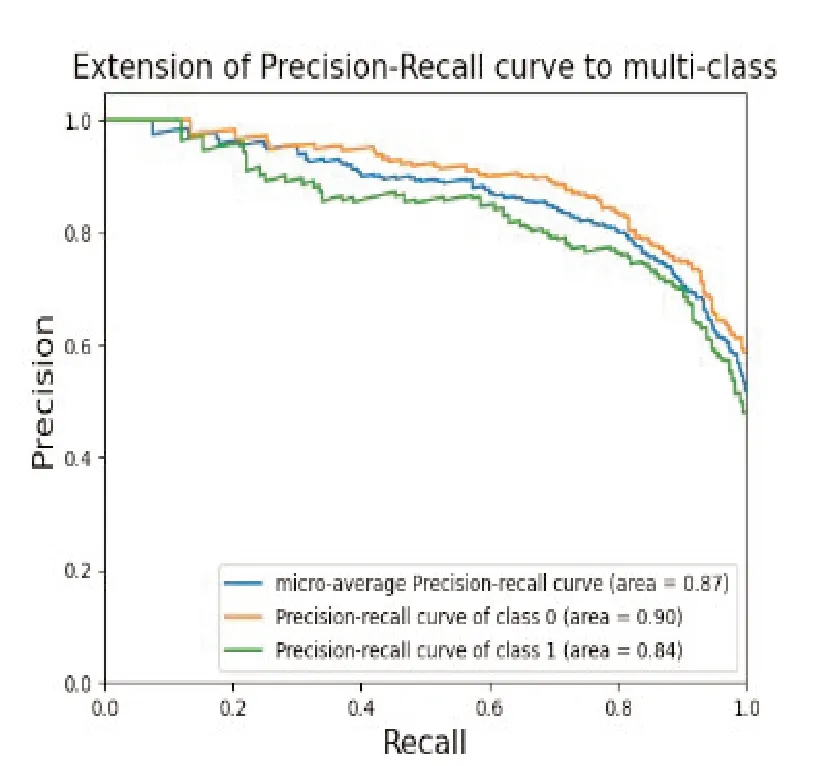
图19 使用二阶差分MFCC的PR曲线

PR 曲线绘制了在不同概率阈值下，模型的精确率和召回率之间的变化。曲线越接近坐标（1，1），意味着模型在保持高精确率的同时，能够具有高召回率。也就是说，模型能够正确地识别出正例，并且较少将负例误分类为正例。

4.3 联合特征的性能评价

如上所述，在CNN 网络中，冗余量更为丰富的二阶差分MFCC 比RMS 和Mel 频谱特征更适用于基调声分类这种具有“人文色彩”的主观分类任务。同时，由于联合特征主要以不同维度的特征信息，通过增加通道来实现更好的性能。因此接下来本文尝试使用RMS 和二阶差分MFCC 的联合特征，即总共40 维信息来对基调声二分类器进行训练，以考察这一联合特征是否能够提高分类器的识别能力。图20、图21、图22 和图23 分别为使用该联合特征得到的准确率曲线及损失率曲线、混淆矩阵、ROC曲线和PR曲线。

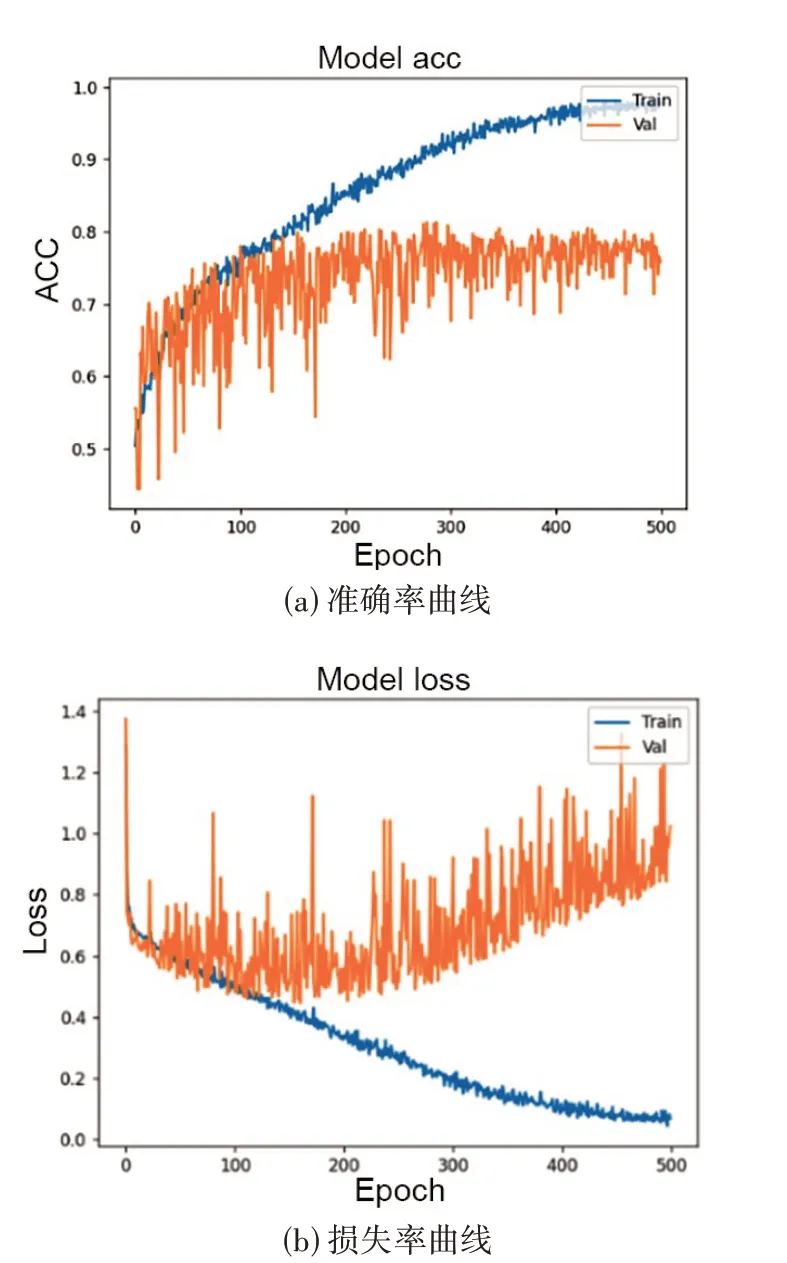
图20 使用RMS与二阶差分MFCC联合特征的识别准确率曲线与损失率曲线

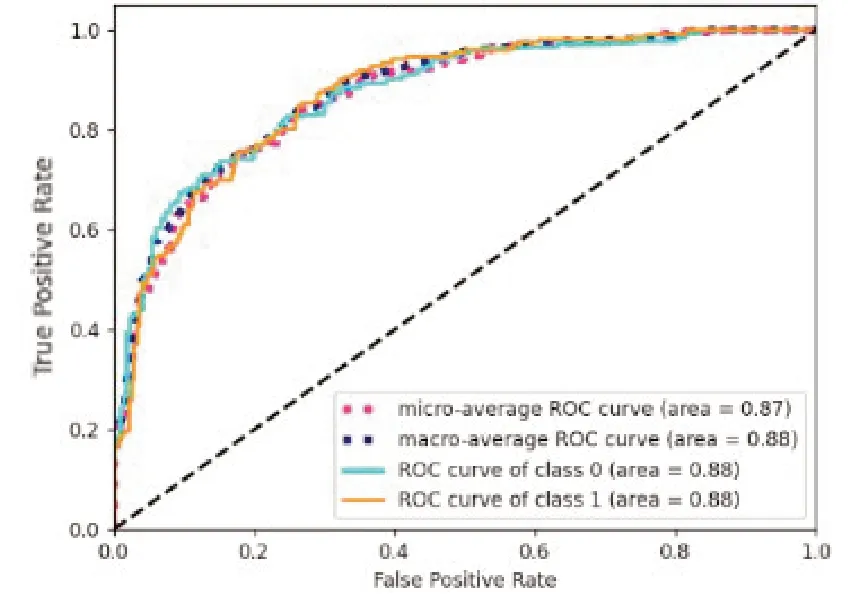
图22 使用RMS与二阶差分MFCC联合特征的ROC曲线

图23 使用RMS与二阶差分MFCC联合特征的PR曲线

由混淆矩阵和上述曲线可知，二阶差分MFCC 特征联合RMS 并没有提高模型识别的准确率，甚至导致准确率下降了0.78%。

5 结论

综上所述，基于本文提出的二阶差分MFCC 特征及网络模型结构进行声景基调声识别的准确率为80.23%，其表现优于单独使用RMS 和Mel 频谱特征的结果，也优于RMS 和二阶差分MFCC 特征的联合使用的结果。作为语音识别中最常用的特征之一，结合本文的数据分析结果来看，MFCC 及其改进的高维特征仍然适用于声景样本的分类；而基于单一能量特征的一维时域RMS 特征可能不适用于声景这类复杂声音的分类任务。

本文仅局限于以老北京中轴线的声景样本数据集为例，针对声景基调声与非基调声的二分类任务，基于CNN 网络深度学习的要求，提出了一种在该分类任务中表现良好的高维二阶差分MFCC 特征，并与单独使用RMS 和Mel 频谱特征，以及使用RMS 和二阶差分MFCC 联合特征，进行了性能上的初步比较。而对于声景这类具有“人文色彩”的复杂声音的主观分类任务，对抗性生成网络等其它类型深度学习模型的性能，以及更多高维特征的选择与提取都需要更为深入的研究。