基于光谱库优化学习的光谱超分与分类精度提升

韩晓琳，张欢，孙卫东

清华大学 电子工程系,北京 100084

1 引言

高空间分辨率高光谱图像可同时提供丰富的空间与光谱信息，已广泛应用于环境监测、精准农业、地物分类、目标检测等不同领域。但高光谱成像过程中光谱分辨率的提升，使得光谱带宽变窄，需要采用较大的瞬时视场才能积累足够多的能量以维持较高的信噪比，这导致其空间分辨率降低（Akhtar 等，2014；Li 等，2021）。与高光谱图像相比，多光谱图像具有更高的空间分辨率，但光谱信息匮乏，这制约了其在相关领域，特别是在材质识别等光谱目标识别领域的可适用性（Zhu 等，2011）、地物分类（Yokoya 等，2017）。近年来，以混合像元分解（Lan 等，2018）、地物分类等为代表的地物光谱库应用技术发展迅猛。由混合像元分解理论可知，自然遥感图像中蕴含的光谱信息是稀疏的，因此多光谱成像中丢失的光谱信息有望借助光谱库，以后处理的形式加以恢复重建。即，利用光谱库提供的全类别光谱信息，在稀疏表示框架下，通过高分多光谱图像恢复重建高分高光谱图像。这不仅有助于提高对地表地物的检测与识别能力，也可用于研发轻小型高分高光谱成像设备。

现有的高分高光谱图像超分辨率重建算法，经历了从融合到恢复重建的发展过程，主要分为基于全色锐化、基于空间字典和基于光谱字典的3 大类别。基于全色锐化的融合重建是指在同一场景下，将低分多光谱与高分全色图像加以融合（Loncan等，2015）。以此为目的，Carper等（1990）提出了用全色图像替代HIS空间中多光谱图像的亮度分量，以获取高分多光谱图像的方法。Aiazzi 等（2007）提出了一种基于多元回归增强的成分替代方法，进一步提升全色锐化效果。Wang等（2017）利用全色图像构建的空间字典，提高了多光谱图像的空间分辨率。Zhu等（2012）利用多光谱与全色图像块的联合稀疏表示，提出了J-SparseFI 算法。Grohnfeldt 等（2013）将该算法进一步拓展为利用高光谱与多光谱图像恢复重建高分高光谱图像的算法，但该算法中的全局字典学习过程易导致较高的计算成本。

为了进一步提升高分高光谱图像的重建质量，Wei等（2015）利用过完备空间字典恢复重建高分高光谱图像。Zhao 等（2016）提出了一种基于协同表示的重建算法，该算法利用局部自适应空间字典对高光谱与多光谱图像进行稀疏表示。同时考虑到计算成本，该算法中的空间字典由图像块及其近邻图像块构成。Ghasrodashti 等（2017）提出了一种基于光谱解混和贝叶斯稀疏的算法，该算法利用两个加权字典以提高待重建高光谱图像的空间分辨率。

鉴于上述基于空间字典的超分辨率重建算法的光谱保持能力有限，人们进而开始研究基于光谱字典学习的超分辨率重建算法。其中，基于线性混合模型（Keshava和Mustard，2002），Kawakami等（2011）在自然高光谱图像重建中，将同一场景的多光谱与高光谱图像对作为训练数据，利用学习获得的光谱字典作为光谱表达的基元。相似的方法也运用在高光谱遥感图像中（Huang 等，2014），其中光谱字典改由纯净光谱构成。Yokoya等（2012）提出的耦合矩阵分解算法，将高光谱图像分解为端元与丰度矩阵，其端元矩阵可看作是一种特殊形式的光谱字典。该算法在丰度非负及归一化约束下进行求解，用来提升高光谱图像的空间分辨。Simões 等（2015）提出了一种基于子空间变分约束的图像融合方法，其光谱字典由端元光谱构成。Veganzones等（2016）提出了一种基于图像块端元的全局光谱字典学习算法，较好解决了高光谱图像重建中的低秩病态问题。Akhtar等（2014）提出了一种非负约束下的空间—光谱稀疏表示算法，该算法在相似光谱具有相同丰度这一假设下求解光谱字典。Dong 等（2016）提出了一种基于非负稀疏表示的融合算法，利用近邻光谱的相似性和稀疏先验联合求解光谱字典和稀疏系数。Chen 等（2019）提出了一种基于光谱字典学习的超分辨率重建算法，该算法利用不同场景多光谱—高光谱图像对提供的光谱映射关系进行超分辨率重建，并利用辅助高光谱图像学习得到光谱字典。此外，为了同时利用光谱与空间信息，Zhang 等（2016）利用两个字典分别用于表达空间和光谱域中图像潜在结构，Nezhad 等（2016）也提出了一种基于光谱解混的算法，同时使用空间和光谱字典提升高光谱图像的空间分辨率。

基于单幅图像的空间超分辨率重建是指利用先验知识或样本学习获取额外的附加信息，进而由低分高光谱图像重建高分高光谱图像。目前，基于深度学习的算法在单幅图像的高光谱图像重建中获得了较好的效果。其中，Yuan等（2017）利用迁移学习和卷积神经网络（CNN）（Dong，2014）实现了由低分高光谱图像重建高分高光谱图像。Hu 等（2017）提出了一种光谱差异学习算法，利用CNN 进行高分高光谱图像重建。Mei 等（2017）在利用CNN 提升高光谱图像的空间分辨率时，引进了3D 卷积神经元。Ertürk 等（2014）提出了二元粒子群优化算法（BPSO），该算法在不使用任何额外高空间分辨率图像的情况下，提升了高光谱图像的空间分辨率。Villa等（2010）提出了一种基于模拟退火的算法来提升高光谱图像的空间分辨率。Pan 等（2014）利用光谱和结构相似性，提出了单幅高光谱图像恢复重建算法。为了进一步利用高光谱图像的内在几何结构和字典基元之间的不相关性，Lu等提出了一种稀疏编码算法（2014），以获得更好的超分辨率重建性能。需要指出的是，上述恢复重建算法旨在提高低分高光谱图像的空间分辨率，而非光谱分辨率。

自20 世纪70 年代以来，不同机构逐渐建立了众多光谱库，如美国地质调查局（USGS）、喷气推进实验室（JPL）和约翰霍普金斯大学（JHU）等。这些光谱库已被广泛应用于高光谱图像分类、光谱解混以及ENVI 等商业软件。其中，Iordache等（2014）提出了一种利用光谱库进行端元矩阵估计的算法。Xu 等（2016）提出了一种光谱库与像素的混合结构，用以改善端元提取性能。Ertürk等（2016）提出了类似的算法，并用于高光谱图像的变化检测。

利用低分高光谱图像进行光谱字典学习是一种有效的高分高光谱图像恢复重建方法，其中，光谱字典的每一列代表一条纯净的光谱端元。然而，在实际应用中，光谱端元的数量难以确定，尤其是在含有弱小光谱目标的情况下。且在光谱解混中，先验信息通常用于保证分解的唯一性，但先验信息的设计和评价是十分困难的。此外，高光谱图像融合或重建过程中对同一场景或不同场景多光谱与高光谱图像的依赖也制约了其普适性。针对上述问题，基于光谱空间的高度稀疏性，Han等（2019）提出了一种基于光谱库的高分高光谱图像重建方法，该方法利用光谱库提供的光谱信息与高分多光谱图像提供的空间信息，实现了单帧高分多光谱图像的光谱超分辨率。其核心是基于光谱库的光谱字典学习与基于高分多光谱图像的稀疏系数求取，一般来讲，光谱信息与空间信息的协同利用、以及光谱字典与稀疏系数求取精度的进一步提升有助于改善光谱超分辨率重建质量。因此，本研究提出了一种基于光谱库优化学习的光谱超分辨率重建方法SODL（Spectral super-resolution using Optimized Dictionary Learning via spectral library）。SODL 与Han 等提出的方法相比，同样利用单帧高分多光谱图像进行光谱超分辨率重建，但本研究在更为严格的理论推导下，构建了光谱字典与稀疏系数的优化学习过程，同时利用了光谱库提供的光谱信息与高分多光谱图像提供的空间信息，实现了更高精度更为稳健的、由单帧高分多光谱图像到高分高光谱图像的光谱超分辨率重建。

2 光谱超分辨率重建模型

设高分高光谱图像由X∈Rλx×N表示，高分多光谱图像由Y∈Rλy×N表示，光谱库由Z∈Rλz×M表示。其中，N和M（一般应用场景下通常N≫M）分别表示X和Z各波段中的像素数，λx、λy和λz(λz≥λx≫λy)分别表示X、Y和Z的光谱波段数。则，观测图像Y可以表示为X的光谱退化：

为了利用光谱库Z提供的光谱信息重建X，需要在空间和光谱上建立X与Z的关系。在光谱上，其光谱分辨率（包括波长和波段数）可能有所不同，因此需要利用矩阵对Z进行波段匹配，即匹配后的光谱库可表示为PZ；在空间上，如果光谱库Z涵盖了X中的所有地物种类，X与Z的关系可视为从属关系，由于Dx和Dz可以分别表示X与PZ，本文假设从属关系也存在于Dx和Dz中，

式中，Aq=QAx为等价稀疏系数矩阵，Dp=PDz为匹配后的光谱字典。以上处理过程的主要目的是通过光谱字典，将普通光谱库Z映射为与待重建高光谱图像X波段对应的特定光谱库。此时，可通过式（4）估计匹配后的光谱字典Dp与等价稀疏系数矩阵Aq，从而超分重建出高分高光谱图像X。

3 光谱超分辨率重建方法

3.1 波段匹配

通过光谱上的波段匹配矩阵P，即可实现X与Z之间的波段匹配过程，P的求解可描述为以下最小距离问题：

3.2 光谱字典优化学习

获得波段匹配矩阵P后，根据波段匹配与空间从属关系，式（1）可进一步表示为

同时，考虑到光谱信息多存在于匹配后的光谱库PZ中，即PZ=PDzAz=DpAz，匹配后的光谱字典Dp与等价稀疏系数矩阵Aq可以通过求解以下凸松弛后的优化函数获得：

式中，η用于平衡空间误差与光谱误差，正则化参数λ1与λ2用于平衡表示误差和稀疏性。利用收敛性迭代策略，通过分别优化以下3个子问题，可以获得上述凸优化问题的解：

式中，J(Aq，Az，Dp)表示式（7）中的目标函数，k为迭代次数。

在固定稀疏系数后，光谱字典Dp可根据式（9）优化求解。式（9）可细化表示为

由于最小化式（11）中两项之和比分别最小化每一项更具挑战性，本文采用分裂策略利用ADMM 算法（Boyd 等，2011）求解上述凸问题。此时，式（11）的拉格朗日函数可以描述为

式中，V1 为拉格朗日乘子，S=DpAq表示分裂变量。以上最小化问题可以进一步描述为对Dp和S最小化的子问题：

式（13）中的所有子问题的闭式解可以表示为

3.3 稀疏系数优化学习

采用与式（9）相似的分裂优化策略，利用ADMM 算法优化求解式（8）与式（10），从而获得稀疏系数Az与等价稀疏系数矩阵Aq的闭式解：

式中，Dl=LDp表示低光谱分辨率字典，B=Az与C=Aq表示分裂变量，V2与V3为拉格朗日乘子。

综上所述，本研究将光谱库中的光谱信息作为先验，通过综合利用光谱库提供的光谱信息与高分多光谱提供的空间信息，进行光谱字典及其稀疏系数优化学习，实现了仅由一幅高分多光谱图像光谱超分辨率重建高分高光谱图像的目的。本研究建立的SODL 方法的总体算法框架见图1。基本算法流程如下。

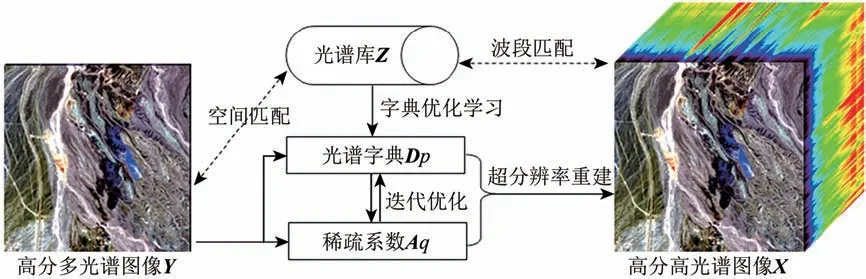
图1 本研究建立的SODL方法的总体算法框架Fig.1 Overall framework of the proposed SODL method

步骤1 输入光谱库Z、多光谱图像Y、波段信息Wx、光谱响应函数L，设置参数η、λ1、λ2、μ1、μ2、μ3，光谱字典列数K，迭代次数T1、T2。

步骤2 通过式（5）求解波段匹配矩阵P；

步骤3 通过式（15）求解光谱字典Dp，迭代T1次后终止；

步骤4 通过式（16）与式（17）求解稀疏系数Az与等价稀疏系数矩阵Aq，迭代T2次后终止；

步骤5 通过式（8）至式（10）迭代更新步骤3至步骤4；

步骤6 输出高分高光谱图像X⌒←DpAq。

4 结果与分析

通过3组实验分别从定性评价、定量分析、以及分类性能提升效果3个方面验证本文方法的有效性与实用性。实验采用均方误差MSE（Mean Square Error）、峰值信噪比PSNR（Peak-signal-tonoise ratio）、光谱角SAM（Spectral Angle Mapper）、通用图像质量指数UIQI（Universal Image Quality Index）以及平均结构相似性ASSIM（Averaged Structural Similarity）进行评价。其中ASSIM=为各波段结构相似性（Wang等，2004）指标。除了将SODL 方法与仅利用一幅高分多光谱图像进行光谱超分辨率重建的HIRSL算法进行对比外，还与G-SOMP+、SASFM、LACRF、NSSR 等同时利用同一场景高分多光谱与低分高光谱图像的重建算法进行了比较。

4.1 模拟数据对比

为了排除成像环境、成像噪声等对超分辨率重建过程有可能产生的不利影响，在理想环境下对本文所提算法的理论性能加以评价，模拟数据对比实验选用了USGS 光谱库中480 条典型矿物光谱，其光谱覆盖范围为400—2500 nm。选择了其中400 个97 波段的、可均匀覆盖上述光谱范围的不同光谱数据，模拟构建20×20×97 像素的理想高光谱图像，以排除实际高光谱成像中的噪声影响。为了模拟光谱混合过程，本实验采用尺寸为8×8的高斯模糊核对该理想高光谱图像进行了空间模糊，从而得到本组实验的高分高光谱参考图像。再利用覆盖可见光与近红外波段的IKONOS-like光谱响应函数对参考图像进行光谱退化，获得尺寸为20×20×4 像素的模拟高分多光谱图像。同时，对参考图像进行σ=3、5×5 的高斯模糊以及因子为2 的降采样，获得尺寸为10×10×97 像素的同一场景低分高光谱图像，以满足对比算法对高分多光谱与低分高光谱图像同时获取的要求。受限于低分高光谱图像的尺寸，对比方法中的光谱字典列数设置为100。在仅利用一幅高分多光谱图像的SODL方法中，匹配光谱字典列数设为480，以更多地保留光谱库中的光谱信息。迭代次数T1、T2 分别设置为30 与1，拉格朗日函数中的参数分别设置为λ1=λ2=10-4、μ1=μ2=μ3=10-2。

表1 比较了在平均MSE、PSNR、UIQI、SAM和ASSIM 指标下不同算法的重建效果，其中粗体字标示的数值为最优。结果表明，SODL 方法不仅在ASSIM 指标上优于SASFM 和G-SOMP+算法，而且在MSE、PSNR和UIQI评价指标上优于G-SOMP+算法。具体分析如下：与SASFM、G-SOMP+算法相比，SODL 方法将ASSIM 指标由0.9882、0.9915提高到了0.9947；与G-SOMP+算法相比，SODL方法中，PSNR 由48.4157 dB 提高到了48.8755 dB，说明重建图像质量至少改善了0.45 dB。上述结果表明：即使G-SOMP+等算法同时利用了多光谱与高光谱图像，SODL 方法仍在空间结构上恢复重建出了更多的细节，获得了较好的重建高分高光谱图像质量；与利用同一场景低分高光谱图像作为附加信息的重建算法不同，SODL 方法的输入仅为一幅高分多光谱图像，因此其SAM 指标稍差，为1.1911°，但与G-SOMP+算法的1.2322°、SASFM算法的0.9072°、以及NSSR 算法的1.1130°相比，相差不大；与未进行光谱字典与稀疏系数优化学习的HIRSL 算法相比，SODL 方法的PSNR 至少提高了0.32 dB，SAM 指标至少改善了0.02°，说明该方法在光谱超分重建上具有更高的准确性。

表1 模拟数据下不同算法间定量评价指标对比结果Table 1 Comparison results between different methods on the simulated data

图2 比较了不同算法下重建图像的光谱曲线。与其他超分辨率重建算法相比，SODL 方法在仅利用一幅高分多光谱图像的情况下，较好的保持了光谱向量的趋势。从图2 中重建光谱向量可以看出，在第50 和第85 波段附近，SODL 方法的光谱重建准确性甚至优于G-SOMP+算法。

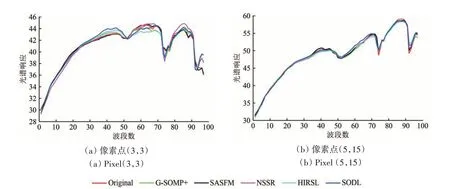
图2 模拟数据下不同算法间重建光谱比较Fig.2 Comparison results in the spectral domain between different methods on the simulated data

4.2 真实数据对比

为了在实际成像环境下评价SODL 方法的可靠性和有效性，进行了真实数据对比实验。该实验采用AVIRIS 机载成像系统于1997年6月19 日获得的高光谱图像作为参考图像，尺寸为300×300×97像素、光谱覆盖范围为683—1978 nm。如图3（a）所示，去除了水汽吸收影响较大的第1—2、105—115、150—170和223—224波段，并利用IKONOSlike 光谱响应函数对参考图像进行了光谱退化，得到尺寸为300×300×4像素的高分多光谱图像。光谱库则同样采用了USGS 光谱库中480 条典型矿物光谱。同时，为满足对比算法对高分多光谱与低分高光谱图像的同时获取要求，对参考图像采用σ=3、7×7 模糊核进行了高斯模糊以及因子为6 的降采样，从而获得了尺寸为50×50×97 像素的同一场景低分高光谱图像。为了具有可比性，所有算法中的光谱字典列数设置为480，其余参数与上节实验保持相同的设置。

图3 重建前后的假彩色图像示意图Fig.3 False color images before and after reconstruction

表2 为AVIRIS 数据下不同算法的平均MSE、PSNR、UIQI、SAM 和ASSIM 指标对比分析结果，粗体标示的数值为最优。其中，由于NSSR 算法中光谱字典列数超出了其最优重建效果范围，该算法的重建效果较差。可见：与同时利用高分多光谱与低分高光谱两幅图像的G-SOMP+、SASFM、LACRF 以及NSSR 算法相比，SODL 方法在仅利用一幅高分多光谱图像的情况下，重建效果仍具有很好的可比性；与未进行光谱字典与稀疏系数优化学习的HIRSL 算法相比，重建出的高分高光谱图像具有更高准确度。值得注意的是，SODL 方法在ASSIM 指标下具有最优重建效果，这表明其在空间结构中保留了最多的细节信息。此外，SODL方法在SAM、MSE 和PSNR 指标下优于NSSR 与HIRSL 算法，在UIQI 指标下比同时利用附加图像的LACRF 和G-SOMP+算法的重建效果更好。图4为不同算法下重建图像的光谱曲线的比较。可见与其他超分辨率重建方法相比，SODL 方法的重建光谱较好保持了原光谱的变化趋势。

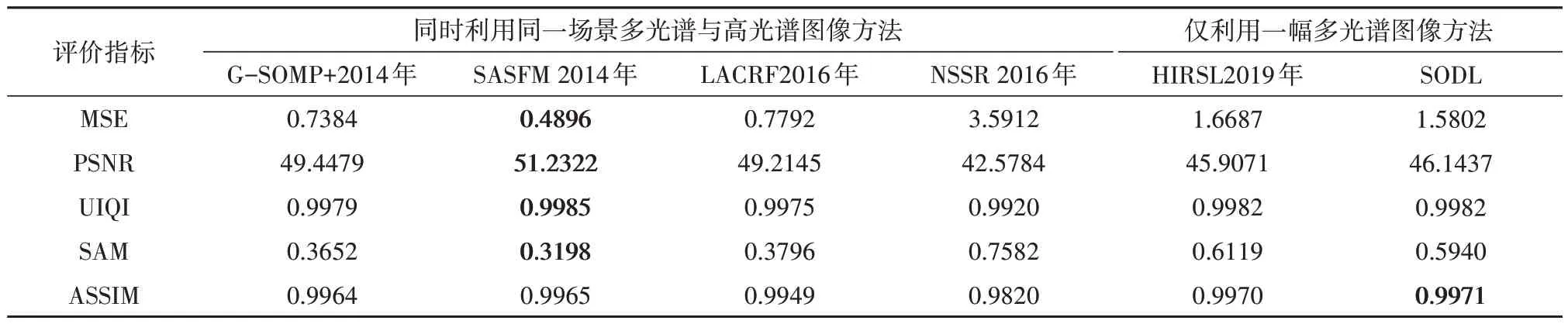
表2 AVIRIS数据下不同算法间定量评价指标对比结果Table 2 Comparison results between different methods on AVIRIS data

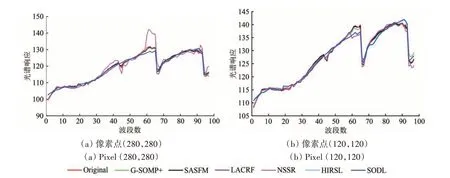
图4 AVIRIS数据下不同算法间重建光谱比较Fig.4 Comparison results in the spectral domain between different methods on the AVIRIS data

4.3 超分辨率重建图像分类精度提升效果分析

采用USGS光谱库中480条典型矿物光谱与18条典型植被光谱数据，每条光谱含有420个波段，同时将地物分类精度测试用、公开高光谱图像Indian Pines 和University of Pavia 数据集作为实验数据，再利用涵盖可见光和近红外波段的IKONOS-like光谱响应函数对Indian Pines 数据进行光谱退化，生成尺寸为145×145×4 像素的高分多光谱图像，SODL 方法超分辨率重建后的高分高光谱图像尺寸为145×145×200 像素。采用相似的光谱退化，由University of Pavia 数据获得的高分多光谱图像尺寸为610×340×4 像素，SODL 方法超分辨率重建后的高分高光谱图像尺寸为610×340×103像素。实验同时采用了Ni 和Ma（2015）提出的NC-SVM 方法、以及Xu 等（2018）提出的RPNet 方法，分别对高分多光谱图像、以及超分辨率重建后的高分高光谱图像进行了地物分类。在有监督分类过程中，Indian Pines 数据5%的标注样本、以及University of Pavia数据1%的标注样本将作为有监督分类的训练数据，并对各分类结果采用总体正确率OA（Overall Accuracy）进行评价。

图5—8 分别为NC-SVM 方法及RPNet 方法在Indian Pines 及University of Pavia 数据上的分类结果。可见：与高分多光谱图像相比，利用SODL 方法进行超分辨率重建后的高分高光谱图像具有更高的地物分类准确度。即对于NC-SVM 方法，在两个数据集上的OA 指标分别提升了11.0%与0.94%；RPNet 方法在两个数据集上的OA 指标分别提升了0.33%与1.24%。由此可见，采用不同类别的高光谱地物分类方法，光谱超分辨率重建后高分高光谱图像的地物分类精度均有一定幅度的提升，说明SODL 方法具有普适性及其实际应用价值。

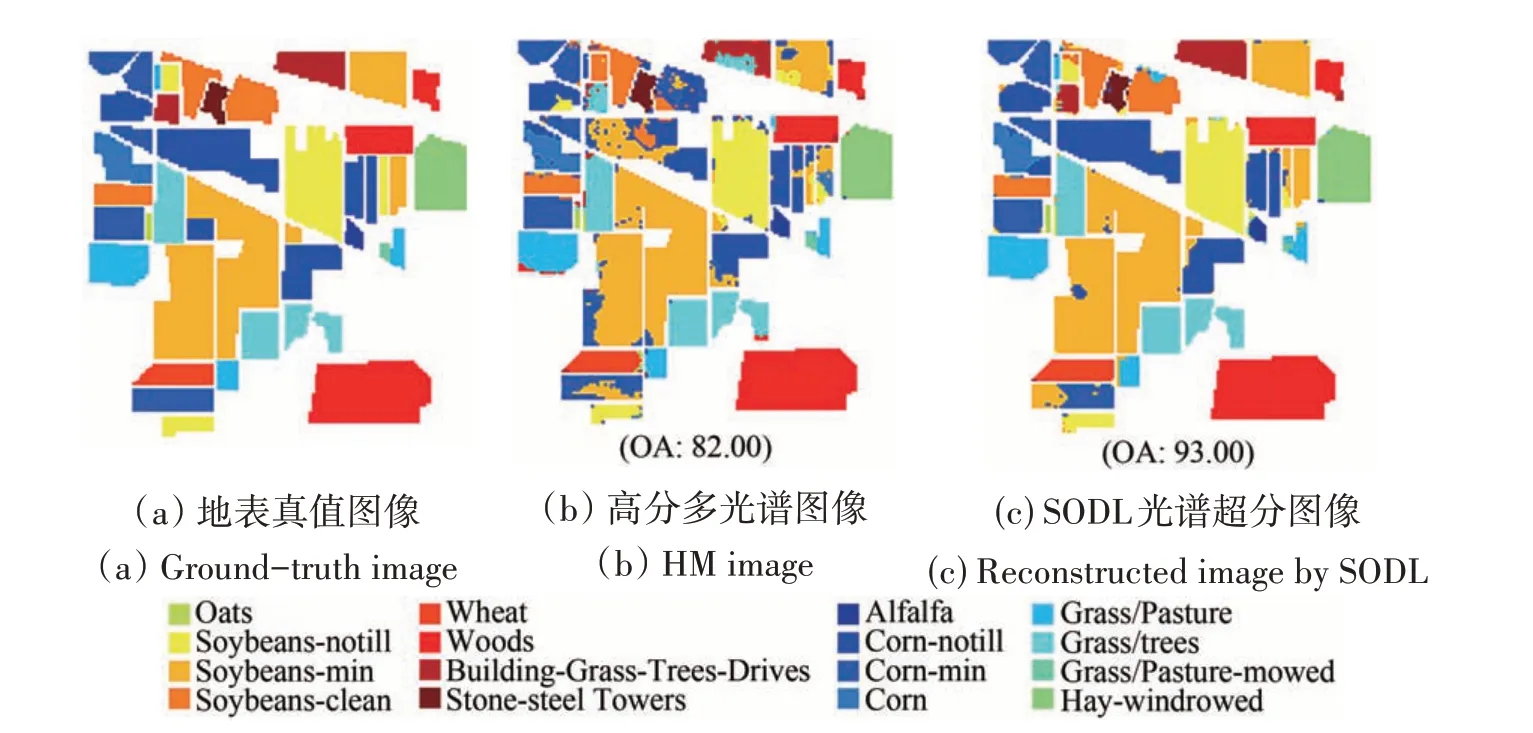
图5 Indian Pines数据集下NC-SVM方法分类结果Fig.5 Classification results on the Indian Pines dataset by NC-SVM method

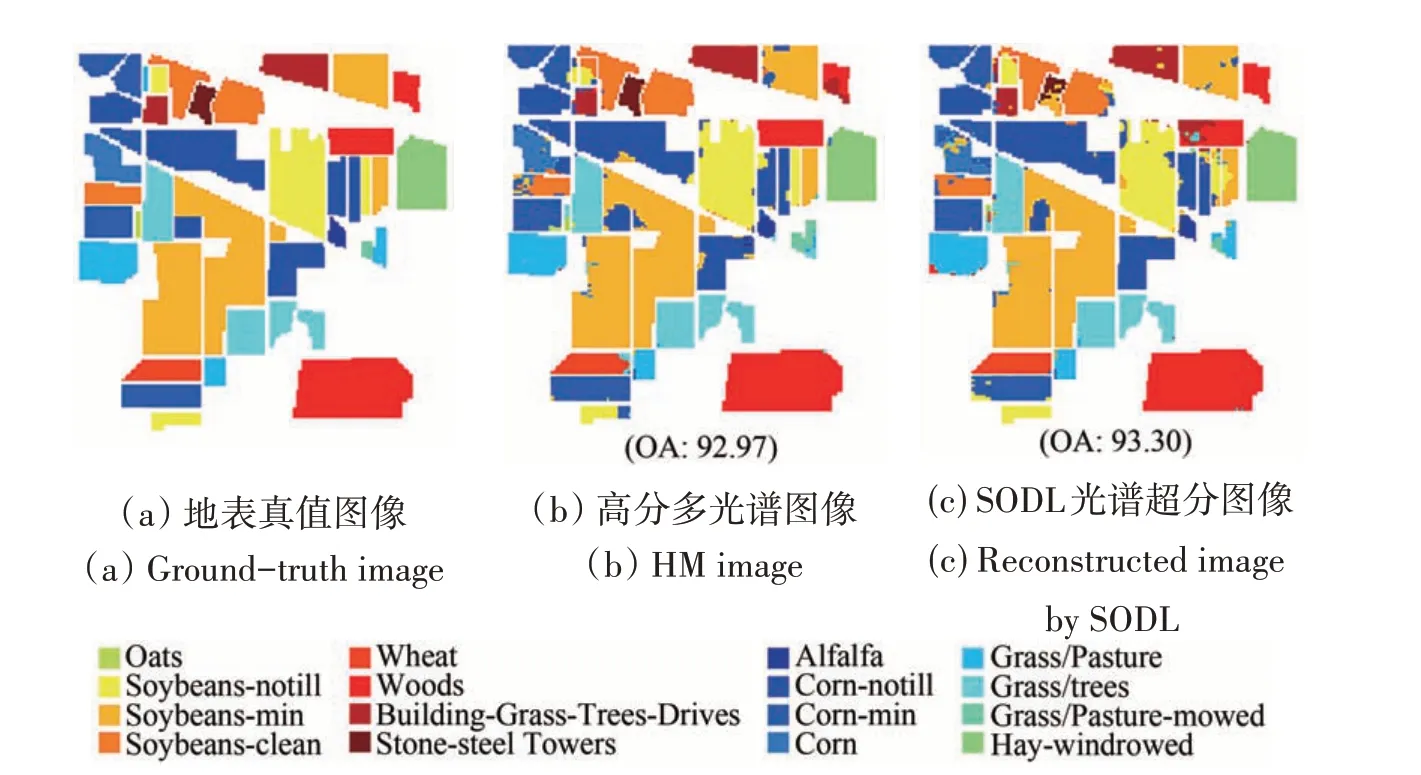
图6 Indian Pines数据集下RPNet方法分类结果Fig. 6 Classification results on the Indian Pines dataset by RPNet method

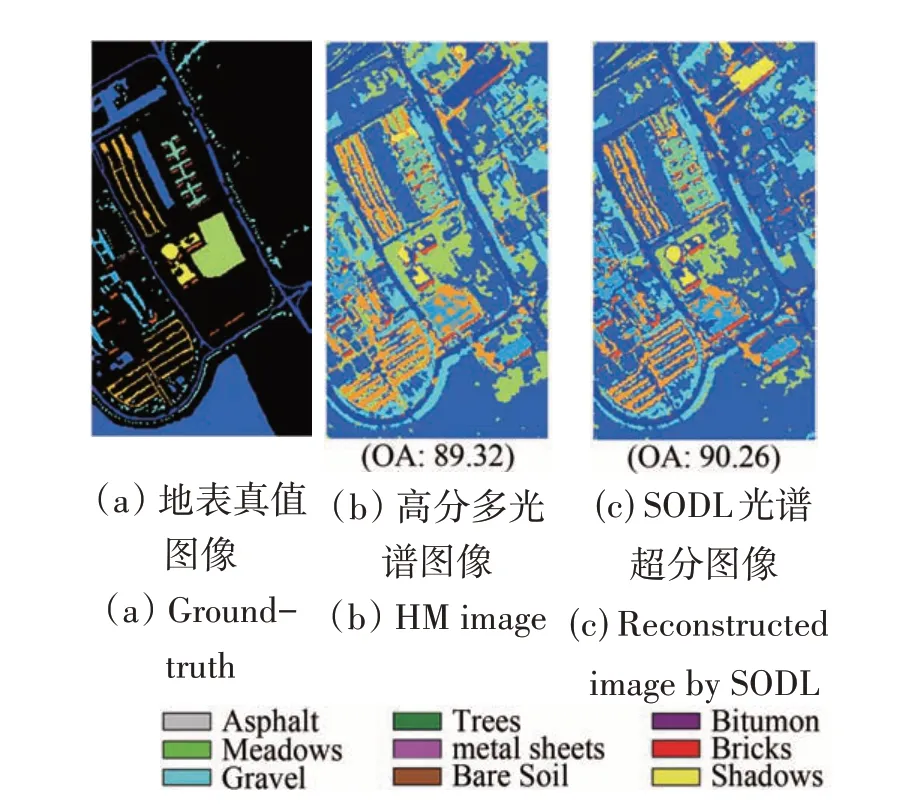
图7 University of Pavia数据集下NC-SVM方法分类结果Fig. 7 Classification results on the University of Pavia dataset by NC-SVM method

图8 University of Pavia数据集下RPNet方法分类结果Fig. 8 Classification results on the University of Pavia dataset by RPNet method

4.4 计算复杂度分析

SODL 方法复杂度主要由波段匹配、光谱字典优化学习与稀疏系数优化学习3 部分构成。其中，波段匹配的复杂度为O(λxλz)。根据式（15），光谱字典优化学习中更新Dp和S的计算复杂度分别为O(T1(λxKN+K3+NK2)) 与O(T1(λyλx2+λx3+λxKN))；与Han 等（2019）所提方法的分析类似，根据式（16）与（17），稀疏系数优化学习中更新Az、B、Aq与C的计算复杂度分别为O(M)、O(T2(λxK2+K3+λxKM))、O(N)与O(T2(λyK2+K3+λyKN))。因此，在λy≪λx≪K≪N的一般应用场景下，本文所提方法的总计算复杂度为O(T1NK2+T2(λxKM+λyKN+K3))。

5 结论

本文提出了一种基于光谱库优化学习的光谱超分辨率重建方法，简称SODL 方法。该方法利用波段匹配，将光谱库映射为与待重建高分高光谱图像波段对应的特定光谱库；综合利用特定光谱库提供的光谱信息与高分多光谱提供的空间信息，进行光谱字典优化学习与稀疏系数矩阵估计，进而实现了仅由一幅高分多光谱图像到高分高光谱图像的超分辨率重建。模拟与真实数据集、以及多种图像质量评价指标下的光谱超分辨率重建对比结果表明，虽然SODL 方法仅使用了一幅高分多光谱图像，但与同时使用高分多光谱图像与低分高光谱图像的其他超分辨率重建算法相比，其在重建效果上具有很好的可比性，部分指标甚至更优；与未进行光谱字典与稀疏系数优化学习的相关算法相比，SODL 方法重建的高分高光谱图像具有更高准确度；同时，光谱超分辨率重建后的高分高光谱图像可显著提升地物分类精度。SODL 方法可为促进轻小型高分高光谱成像设备的研发，为小卫星及无人机平台提供更为可行的高光谱成像手段。