应用Sinkhorn距离和图正则约束的高效解混算法

杨露露，李春芝，陈晓华，王丽

湖州师范学院 信息工程学院,湖州 313000

1 引言

高光谱遥感技术作为一种新型对地观测技术，提供了丰富的地物光谱信息，能够对地物目标进行识别（Zhang 等，2019）和精细分类（Ghamisi等，2017；Khan等，2018），逐渐成为当前遥感技术研究前沿。由于受空间分辨率的限制，高光谱图像中单个像元包含多种地物使得混合像元的现象普遍存在，成为像元级应用精度难以提高的主要问题（蓝金辉 等，2018）。因此，对混合像元进行分解，通过提取构成像元的各类基本物质组成成分的光谱特征以及这些物质在像元内所占的比例可以提高高光谱遥感定量应用的精度（童庆禧 等，2016；张兵，2016）。

现有的光谱解混方法通常基于线性混合模型（LMM）或非线性混合模型（NLMM）（Heylen 等，2014）。其中，线性混合模型由于简单、易求解得到广泛应用。高光谱盲解混能够同时进行端元提取以及丰度估计，本质上属于信号处理领域中的盲源分离问题（Yao 等，2019）。盲源分离的典型方法有独立成分分析（ICA）（Wang和Chang，2006）和非负矩阵分解（NMF）（Lee 和Seung，1999）。由于ICA对源信号做出的独立性假设与高光谱图像中的丰度和为一约束矛盾，所以在光谱解混中的应用受到了限制（Nascimento 和Dias，2005）。与ICA 相比，NMF 能够更好地适应光谱解混的需求（Tsinos等，2017），但仅有的非负约束易导致NMF陷入局部最优解。因此，需要另外引入合适的约束以获取更好的解混性能。

考虑到LMM凸几何的特点，Miao和Qi（2007）引入端元单形体体积约束，提出最小体积约束NMF（MVCNMF）。受Miao 和Qi 的启发，后继几种基于几何约束的解混算法被提出（Yu 和Sun，2007；Wang 等，2013；Zhi 等，2017）。这些方法首先假设高光谱图像位于一个单形体中，并且其顶点被认为是所要提取的端元。Marrinan 和Gillis（2021）为解决端元的不平衡性问题，提出一种基于块的minimaxNMF 模型来处理含有稀少端元的高光谱图像。此外，由于自然界中地物一般呈现分段的局域同质分布，一个像元不会包含所有端元物质，因此，除了端元的物理约束外，丰度的稀疏性也可以被用于构建NMF解混框架。Qian等（2011）、Yuan 等（2015）、Feng 等（2018）采用L1/2-NMF，与L1范数（Bruckstein 等，2008）相比，结果表明L1/2-NMF更能满足和为一约束，并且在保证丰度稀疏的同时，降低了计算复杂度。进一步地，为保持数据的结构信息，He 等（2016）施加L1，2范数进行联合稀疏约束，解决了L1/2范数易受噪声干扰的问题。Li 等（2016）考虑到同一个端元仅分布在个别像元中，应用L2，1范数对丰度的行和列同时进行稀疏约束。Han 等（2020）融合低秩性约束，引入使丰度更稀疏的L2，p范数。上述方法虽然采取了相关的约束，但忽略了数据的空间信息。Wang等（2017）利用线性迭代聚类分割技术进行空间群稀疏约束，结合丰度的稀疏性提出群稀疏正则NMF（SGSNMF）。Liu 等（2011）融合丰度的分离性和平滑性约束，在保证相同像元中不同端元相关性的同时考虑数据的空间关系。Qin 等（2021）引入图全变差约束（gtv）提高丰度的空间平滑度，其采用交替方向乘子法（ADMM）优化求解，并且融合Nyström 近似策略和Merriman-Bence-Osher（MBO）方法降低求解复杂度。Wang 等（2016）考虑图像的空间和光谱信息，利用超图建模光谱的空间结构以保证相同超边内像元丰度的一致性。此外，由于高光谱数据易受复杂非线性效应影响，Févotte和Dobigeon（2015）提出了鲁棒NMF（rNMF），该算法引入群稀疏离群项克服非线性问题。为挖掘高光谱数据中的非线性结构，Mei 等（2016）、甘玉泉等（2019）、Rathnayake等（2020）将图模型理论嵌入到NMF模型中，以保持数据的局部几何结构。Lu等（2013）在L1/2-NMF的基础上，亦构建了额外的图正则项，保证各端元丰度之间的紧密联系。

现存NMF 解混算法针对端元和丰度的物理含义，分别施加相应的约束以获得更精确的解混结果，但大多基于欧氏距离构造目标函数，而高光谱图像内部结构的复杂性导致简单的线性表示不能很好地度量重构误差。Li 和Chen（2020）提出相关熵诱导度量代替欧氏距离构造的损失函数，克服了基于欧氏距离的建模难以降低重构误差且极易受异常值影响的弊端。受最优传输思想启发，Rubner等（2000）提出地球移动距离（Earth Mover’s Distance，EMD）计算两个分布之间的距离以反映最小需求量。鉴于该最优传输问题，Sandler 和Lindenbaum（2011）提出基于EMD 的非负矩阵分解算法（EMDNMF），并证实EMD对不同维度噪声不敏感，因此，基于EMD 的NMF 算法可以获得比传统基于欧氏距离的NMF算法更鲁棒的性能。

由于高光谱图像内部包含大量不同维度的噪声（Li等，2021），而EMD 具有对不同维度之间噪声不敏感的优势，因此，经过初步理论分析，EMD 比欧氏距离更适用于处理含有复杂噪声的高光谱数据。由Sandler 和Lindenbaum（2011）提出的EMDNMF 在计算机视觉中的应用可知，基于EMD 的NMF 在高光谱数据分析中亦可取得不错的效果。但实际应用中，由于高光谱图像属于复杂大数据，EMDNMF 高额的计算代价导致其在大规模高光谱数据分析中存在一定的局限性。Qian 等（2016）提出了一种基于Sinkhorn 距离的非负矩阵分解方法，可以更简单快速地求解该距离下的分解模型。Zhang 等（2020）进一步引入对偶图正则项，同时考虑数据和特征的流形结构。上述基于Sinkhorn 距离的非负矩阵分解算法被广泛应用于图像聚类并取得了不错的效果。

本文首次将最优传输技术和图模型理论综合应用于高光谱解混中，提出一种基于Sinkhorn距离和图正则约束的高效解混算法（SDGNMF）。该算法在充分挖掘EMD 优点的基础上，对EMD 施加熵正则约束，将EMD 改进为Sinkhorn 距离，并将其作为度量误差的标准，有效降低了计算复杂度。此外，被施加了熵正则约束的EMD，即Sinkhorn距离对模型的表示可以更好地建模不同维度特征之间的关系，特征的相关性得以充分利用。本文在Sinkhorn距离的基础上特别引入图正则约束以进一步刻画数据的流形结构。通过在模拟数据集以及真实数据集上的实验验证，以期有效改善基于NMF的高光谱解混算法性能。

2 理论介绍

2.1 线性光谱混合模型

线性混合模型假设入射光在到达传感器前只与一种地物发生作用，不考虑物质内部反射、散射等作用，混合像元光谱表示为端元光谱与其相应丰度的线性组合，数学表达式定义如下：

式中，X∈RL×N表示原始图像，U∈RL×P表示端元矩阵，V∈RP×N表示丰度矩阵，E∈RL×N表示重构误差矩阵，通常被认为是加性噪声（Akhtar和Mian，2017；Zhang 等，2018）。L为波段数，P为端元数量，N为图像中所含像元总数。矩阵U，V，E均满足非负性约束（ANC），并且丰度V还需满足和为一约束（ASC）。

2.2 非负矩阵分解

NMF 是由Lee 和Seung（1999）提出的一种无监督特征提取方法。对于给定的非负矩阵X，NMF将其分解成两个非负矩阵U和V，使得分解后两个矩阵的乘积近似等于原始矩阵，即X≈UV。

为了衡量原始矩阵对分解因子间的重构效果，需要构造目标函数，定义如下：

式中，Distϕ表示度量距离，通常定义为欧氏距离，基于该距离的目标函数表示为

式中，J（·）表示度量函数，‖ · ‖F表示Frobenius范数。

对于式（3），一般采用乘性迭代算法进行更新，得到U和V如下

式中，（·）T表示矩阵转置。

3 基于Sinkhorn距离和图正则约束的非负矩阵解混模型

高光谱图像内部的复杂性导致数据中相邻元素可能由相似的端元构成，并且对应的丰度也非常接近，可见，高光谱数据中存在着丰富的相关特征。传统解混算法中，普遍采用欧氏距离构造目标函数，无法准确描述高光谱图像中各维度特征间关系。为充分利用图像空间中特征的相关性，本文采用基于Sinkhorn距离测量误差的方法。

3.1 Sinkhorn距离

在本文所提出的SDGNMF 方法中，采用改进的EMD 代替传统欧氏距离构造目标函数。其中，EMD 定义为两个分布直方图之间传输元素的最小代价。高光谱的EMD 原理详见图1，图1中，红框表示选取图像中某一区域。该区域的直方图表示为x；y为经EMD 处理后同一区域的直方图表示；q、p分别表示直方图x、y中的区段号。选取Urban数据集中某一波段的灰度图像，红框框选其某一区域的直方图表示为x；假设x分布直方图和y分布直方图均含有n个区段数，从x分布直方图中选取数据组合为r1的元素，共计个元素，产生转移量可表示为将转移量运送至y分布直方图的各区段中，生成数据组合为r2的元素，即式中，q、p分别表示x、y分布图中的区段号；理想情况下根据上述传输方案依此反复，直至x中所有元素被全部分配至y分布直方图中。EMDdM(x，y)计算公式如下（Rubner等，2000）：

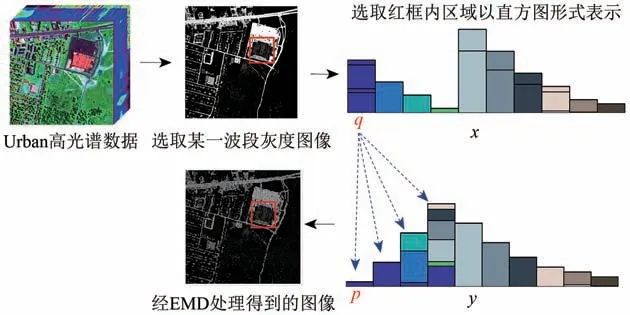
图1 高光谱图像的EMD原理Fig.1 EMD principle diagram of hyperspectral image

式中，Φp表示p区段内元素数，Φq表示q区段内元素数。

由于EMD 计算过程中涉及到线性规划的复杂求解问题，其计算复杂度高达O(n3logn)，限制了其在大规模数据分析中的适用性（Sandler 和Lindenbaum，2011）。本文在EMD 的基础上引入熵正则项平滑参数化模型。将改进后的EMD 距离称为Sinkhorn距离，定义为

式中，1 表示全一向量，⊙表示逐元素乘法；ST表示矩阵S的转置，H(S)=-∑p，qSlogS表示矩阵S的熵，λ表示正则化参数，用于控制熵正则化作用的强度，当λ足够大时，式（7）相当于EMD。

对于上述模型的求解，Cuturi（2013）提出了一种Sinkhorn-Knopps 矩阵缩放算法，即通过生成一系列行和列被交替归一化的矩阵来进行求解。Genevay 等（2019）证明了基于该缩放算法的模型求解复杂度下降为O(n2)，因此，相较于EMD，Sinkhorn 距离可以更快速有效地进行大规模数据分析。Sinkhorn-Knopps矩阵K定义为

然而，模型（7）的优化需严格满足归一化条件，事实上，在高光谱图像中，考虑到各像元的不规则性且相邻像元间具有相似性，输出图像无法被准确表示为归一化的直方图形式，不能严格满足式（7）中的约束条件。因此，本文对式（7）进行松弛，利用KL散度（Kullback-Leibler divergence）对原等式约束进行软惩罚，将模型简化为一个无约束的问题。上述方法的有效性已在Frogner 等（2015）的研究中得到证明，本文将其推广应用到高光谱解混模型中。Sinkhorn距离最终优化为

本文以两个直方图之间传输元素的最小成本为原则构造目标函数，进而采用Sinkhorn距离作为误差的度量标准，其优势具有如下两方面：一方面，基于Sinkhorn距离的模型采用Sinkhorn-Knopps矩阵缩放算法进行求解，相比于EMD，可以更快速有效地分析高光谱大规模数据；另一方面，考虑到高光谱数据中存在着丰富的相关特征，Sinkhorn距离可以克服噪声影响，建模不同维度特征之间的关系，能够充分利用特征间的相关性。因此，相较于传统基于欧氏距离的NMF，基于Sinkhorn距离的NMF 模型，能够更好地提取数据内部结构信息，提高解混精度。

3.2 光谱特征图正则化

高光谱图像中数据通常位于一个低维子流形上。为考虑空间信息并有效挖掘数据的流形结构，本文在利用Sinkhorn距离构造目标函数的基础上对丰度矩阵V施加图正则约束，进一步捕捉数据间的有效特征，从而增强图正则约束描述几何流形结构的有效性。一般地，图正则项表述如下：

式中，Wij表示图正则项权重矩阵，可以通过热核函数计算得到（Lu等，2013），具体计算公式如下：

式中，xi和xj表示数据空间中两个邻近点，τ表示核参数，通常取值为［0，1］。

3.3 SDGNMF模型

综合式（9）、（10）、（11），由Sinkhorn距离构造的解混目标函数定义如下：

式中，Xj表示矩阵X的第j列向量；ξ表示维持特征相关性和数据流形之间平衡的正则化参数。

由式（12）可知，所提出的模型是非凸问题，同时优化U和V是一个NP 难问题。参考Lee 和Seung（2000），Qian 等（2016）将乘性迭代算法应用求解Sinkhorn 距离并证明了该算法在Sinkhorn距离上的收敛性。为将变量交替最小化，本文同样采用乘性迭代算法对式（12）进行求解，当一个变量迭代时，将其他变量固定为常数，每个变量在当前固定的变量上有条件地更新，从而将所提出的模型计算问题分解成两个凸问题。

给定非负矩阵Θ∈RL×P和Ψ∈RP×N作为U和V的拉格朗日乘子，定义拉格朗日函数Γ为

根 据 Karush-Kuhn-Tucker 条 件，即Θ.×U=0，Ψ.×V=0，可以得出U和V的更新规则：

式中，S*表示最优传输矩阵，定义为Sinkhorn-Knopps矩阵K=exp(-λM-1)的对角缩放：

式中，A和B表示两个缩放矩阵，diag(·)表示对角矩阵。Frogner 等（2015）定义了上述两个缩放矩阵的更新规则，具体表达式描述如下：

3.4 算法流程

本文参照虚拟维度算法（Bajorski，2011）计算端元数量，同时采用顶点成分分析（VCA）初始化端元矩阵U，完全约束最小二乘法（FCLS）初始化丰度矩阵V，为了计算图正则项权重矩阵，将核参数τ设置为0.2，并将K-近邻（KNN）的数目设置为5。本文设置最大迭代次数Imax，如果迭代次数大于定义的Imax，则迭代结束。具体算法流程如下：

输入：原始数据矩阵X，参数λ，γ，ξ，τ，KNN数目，最大迭代次数Imax

步骤1：通过VCA-FCLS算法初始化U和V

步骤2：根据式（11）计算权重矩阵W

步骤3：根据式（6）计算距离矩阵M

步骤4：根据式（8）计算矩阵K

步骤5：循环

根据式（17）更新得到A

根据式（18）更新得到B

根据式（16）更新得到S*

根据式（14）更新得到U

根据式（15）更新得到V

直到满足停止条件

输出：U和V

4 结果与分析

为了证明提出算法的有效性，本文分别在模拟高光谱数据集和真实高光谱数据集上进行性能验证，并与GNMF（Lu等，2013），SGSNMF（Wang等，2017），rNMF（Févotte 和Dobigeon，2015），minimaxNMF（Marrinan 和Gillis，2021），gtvMBO（Qin 等，2021），VCA-FCLS 等6 种算法进行对比分析。所有对比算法均设置为原文献中参数。实验平台为CPU 2.9 GHz，内存8 G 的Windows10电脑上进行，使用Matlab2019a进行代码实现。

4.1 选定评价指标

为定量评估所提出SDGNMF 解混算法的性能，本文采用高光谱解混评估中常用的两种评价指标，即光谱角距离（SAD）和均方根误差（RMSE）。SAD 用来评估端元估计值的准确性，RMSE 用来评估丰度估计值的准确性。SAD和RMSE的表达式定义如下：

式中，ui和分别表示第i个端元真实值和估计值；vi和分别表示第i个端元对应丰度真实值和估计值。

4.2 算法收敛性

对SDGNMF 算法的收敛性能的验证结果如图2所示。可见在所有的测试数据集上，算法的重构误差随着迭代次数的增加而减小，当达到一定的迭代次数时，误差达到一个稳定的值。为了保证一致性，在所有数据集上迭代次数均设置为1000次。

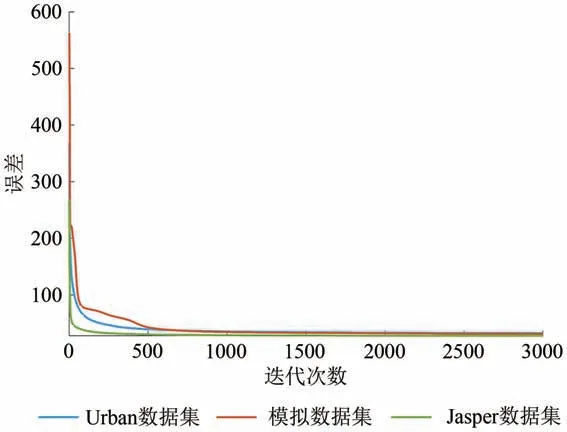
图2 误差随迭代次数变化Fig.2 Figure of error changing with iteration number

4.3 模拟数据集实验

该模拟数据集是根据Hendrix 等（2012）提出的模拟程序生成的，即从美国地质调查局（USGS）光谱库中选择9 种物质221 个波段的谱线作为端元，生成大小为100×100 的图像，图3 展示了9 种端元光谱特征曲线。为满足和为一约束以及非负性约束，通过K均值聚类和高斯滤波器生成相应的丰度图，每个端元对应的丰度值随机分布范围为0.004—0.900，最大丰度值为0.900。

图3 模拟数据端元光谱曲线Fig.3 Endmember spectral curve of simulated data

4.3.1 参数选择

参数λ、γ和ξ分别为正则化参数、松弛参数和平衡参数，分别用于调节熵正则作用的强度、调节模型的松弛程度以及维持特征相关性和数据流形之间的平衡。为研究参数λ、γ和ξ对算法性能的影响，在模拟数据集上，采用固定初始化的方式对3 个参数进行测试。首先，固定γ=ξ=10以测试参数λ对算法性能的影响，参考Qian 等（2016）的研究，参数λ取值从［10，50，100，200，300，400，500］中选取，结果见图4（a）。可见，当λ从10 增加到200 时，SAD 和RMSE 值不断减小并达到最小值，而随着λ继续增加，SAD和RMSE 值呈上升趋势，因此，设置λ=200。其次，固定λ=200，ξ仍设置为10，设置γ取值范围为［10，80］，步长为10 递增，结果见图4（b）。可见，RMSE 值在这区间保持稳定，而当γ=50 时，SAD 达最小值，因此，设置γ=50。最后，固定λ=200，γ=50，设置ξ取值为［1E-6，10］，以10 倍步长增加，结果见图4（c）。可见，参数ξ在1E-6—1E-2变化时，SAD 与RMSE 值均保持稳定。由于参数ξ用于维持特征相关性和数据流形之间的平衡，当ξ＞0.1 时，重构项过于松弛，SAD 和RMSE 估计精度呈明显下降趋势。因此，为了获得更精确的解混结果，将ξ的最优值设置在［1E-6，1E-2］。在以下模拟数据集实验中，参数ξ均设置为1E-4，同时分别设置λ=200和γ=50。

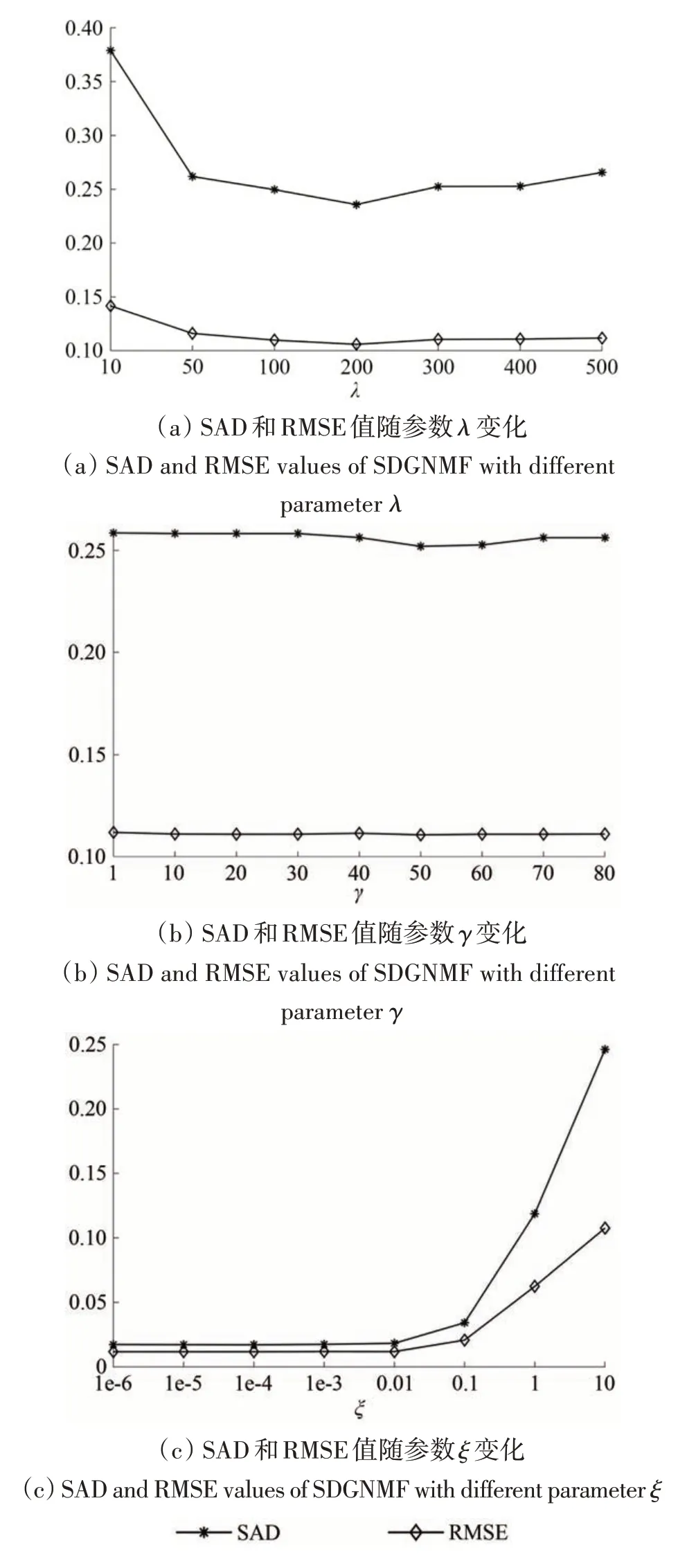
图4 SDGNMF在不同参数下的SAD和RMSE值Fig.4 SAD and RMSE values of SDGNMF with different parameters

4.3.2 鲁棒性分析

在本实验中，旨在对比和分析噪声对算法的影响。在原始无噪声模拟数据集中加入零均值高斯白噪声，信噪比（SNR）定义为式中，X和e分别表示原始信号和其相应的噪声，E[·]表示期望运算符。

为了测试七种算法的鲁棒性，在模拟数据集上添加加性噪声，信噪比分别设置为：10、20、30、40、50、60 dB。每个信噪比下的柱状图从左至右依次为算法SDGNMF、GNMF、SGSNMF、rNMF、minimaxNMF、gtvMBO 和VCA，所有方法的SAD值和RMSE 值均取10 次实验结果的平均值，结果见图5。可见：随着信噪比的降低，所有算法的解混精度都随之降低；在不同的信噪比情况下，所提出的SDGNMF 算法获得的SAD 值和RMSE 值比其他算法更小。因此，实验结果表明，噪声会导致解混结果变差，但所提出的算法相比于其他算法更具鲁棒性。

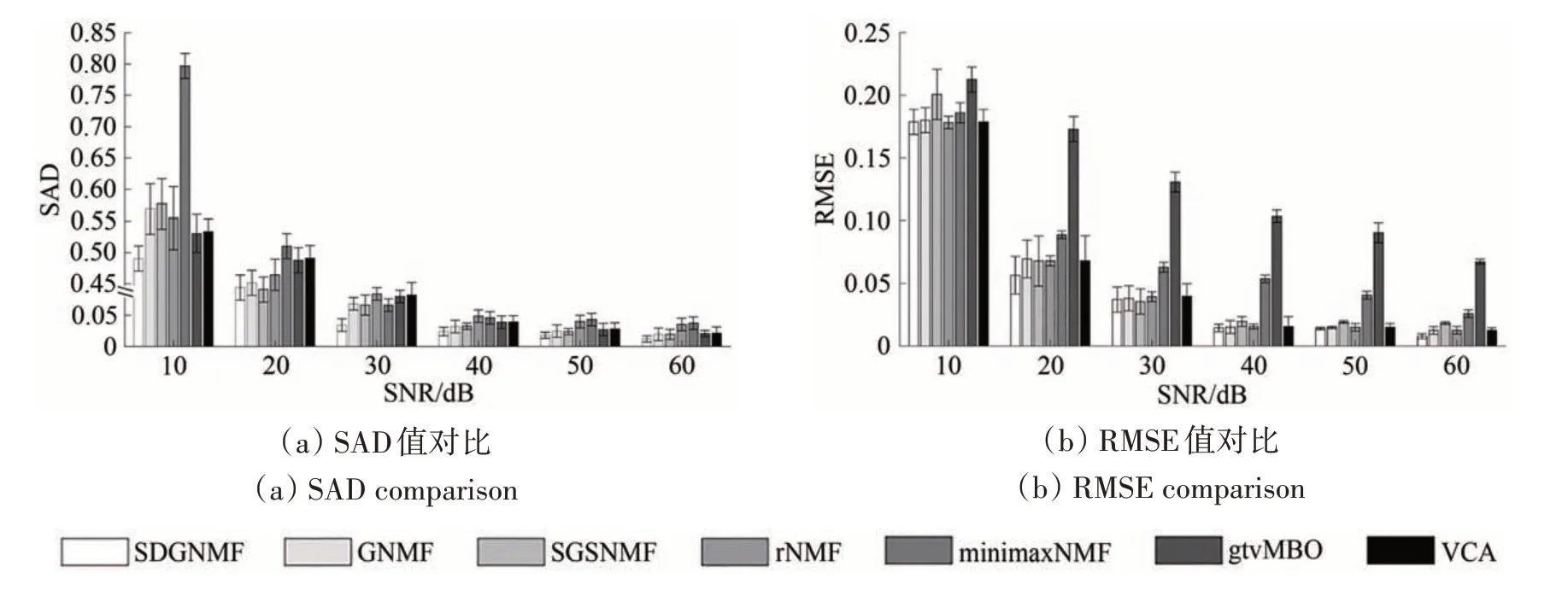
图5 不同SNR下几种算法的SAD和RMSE对比Fig.5 Several algorithms under different SNR with the comparison of SAD and RMSE

4.3.3 不同算法丰度图对比分析

在本实验中，设置参数λ=200、γ=50、ξ=1E-4，对比分析了模拟数据集上其他几种算法提取的丰度效果图，结果如图6所示。

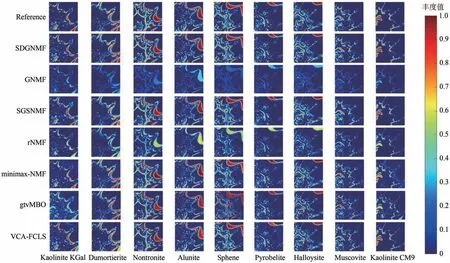
图6 各算法在模拟数据集上的丰度对比Fig.6 Comparison of the abundance maps of each algorithm on simulated dataset

可见，显示SDGNMF、SGSNMF、minimaxNMF以及VCA-FCLS 可以较好地恢复丰度。SGSNMF采用超像素分割法实现空间群稀疏约束，可以保留空间局部信息，但由于没有准确考虑相似像元区域内的不同端元结构，SGSNMF 在得到Kaolinite Kgal端元的丰度图时，误提取了Dumortierite 端元。VCA-FCLS 算法也同样存在上述Kaolinite Kgal端元和Dumortierite端元提取不准确的问题。minimaxNMF在Kaolinite CM9 丰度图中出现了Dumortierite 端元轮廓，且Kaolinite Kgal端元提取精度较低。gtvMBO无法准确区分具有相似结构的端元，导致Kaolinite Kgal 和Kaolinite CM9 端元提取出现混叠。而本文提出的SDGNMF 算法优势在于能够保留迭代后的相似结构，各端元特征之间的相关性得到了充分考虑，因而相邻区域分布的相似物质能够分离出来。相比于其他几种算法，SDGNMF 可以更好地展示局部丰度的细节，获得更真实、完善的丰度图。GNMF 和rNMF 表现欠佳。GNMF 由于无法给出正确的稀疏表示，几乎提取不到有价值的丰度信息，rNMF 获得的丰度图像素值为0.3—0.5，端元提取不纯。综上，解混结果表明所提出的SDGNMF 算法能够更好地恢复模拟数据的丰度图，相比于其他几种对比算法，可以获得更加精确的解混结果。

4.4 真实数据集实验

4.4.1 Urban数据集

Urban 数据集是高光谱解混研究中使用最广泛的高光谱数据之一，可以在网站（http：//lesun.weebly.com/hyperspectral-data-set.html［2021-03-11］）上下载。其子图像大小为307×307，共包含210个波段，波段范围为400—2500 nm，空间分辨率和光谱分辨率分别为2 m 和10 nm。考虑到密集水蒸气和大气效应的影响，去除波段1—4、76、87、101—111、136—153 和198—210 后，保留了162 个波段进行解混。根据实际地面参考图，选取数据集中的6 种端元进行实验，分别是沥青、草地、树木、屋顶、金属和土壤。Urban 数据立方体和6种端元光谱曲线如图7所示。

在本实验中，设置参数λ=300、γ=40、ξ=1E-4，得到的丰度图和地面参考丰度图如图8 所示，表1列出了所有方法的SAD 值，其中粗体表示最优值，下划线表示次优值。从图中可以看出，对比参考丰度图，本文提出的算法恢复了几乎所有的端元成分。VCA-FCLS、gtvMBO 均在沥青丰度图中出现了小范围的草地轮廓，并且VCA-FCLS 未提取到较纯的草地丰度图。GNMF仅提取到了泥土，其他5种端元显示的丰度图颜色均为绿色，即提取纯度较低。对比GNMF，rNMF 丰度颜色值更小，位于0.2—0.3，可见，端元提取很不准确。相较于上述几种对比算法，SGSNMF 和minimaxNMF 得到了相对较好的丰度图，但均由于提取金属时像素值太小，导致准确识别该端元无法实现。此外，表1还表明，SDGNMF 估计出的大部分端元的SAD 值最优，虽然个别提取端元的SAD 值次优，但平均SAD 比其他算法都低。因此，从纯度和准确性的角度来看，本文提出的算法较其余算法能够取得更精确的解混效果。

表1 Urban数据集各算法的SAD对比值Table 1 SAD ratio of algorithms in Urban dataset

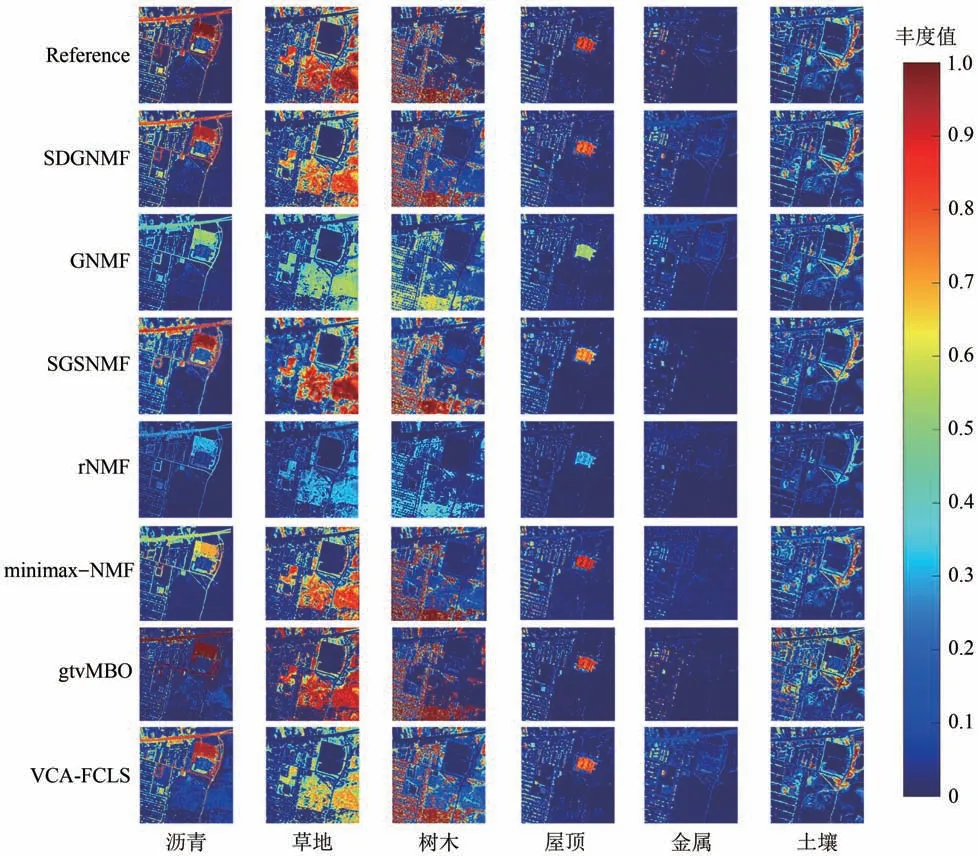
图8 各算法在Urban数据集上的丰度对比Fig.8 Comparison of abundance maps of each algorithm on Urban dataset

4.4.2 Jasper数据集

Jasper 数据集可以在网站（http：//lesun.weebly.com/hyperspectral-data-set.html［2021-03-11］）上下载。其图像大小为512×614，共包含224个波段，范围为380—2500 nm。数据集中含4 种端元，即树木，水，土壤和道路。考虑到水汽波段的影响，去除波段1—3、108—112、154—166 和220—224 之后，保留了198个通道来进行光谱解混。由于此高光谱图像的复杂性，无法精确获取地面实际情况，因此本文采用100×100 大小的子图像进行实验。Jasper数据立方体和4种端元光谱曲线如图9所示。

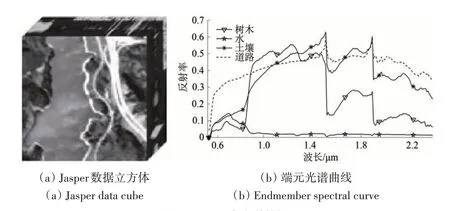
图9 Jasper高光谱数据Fig.9 Jasper hyperspectral data

设置参数λ=300、γ=10、ξ=1E -4，实验得到的丰度图和地面参考丰度图如图10 所示，表2列出了所有方法的SAD值，其中粗体表示最优值，下划线表示次优值。从图中可以看出，本文提出的算法比其他方法更好地恢复了丰度图，与参考地物分布十分吻合。VCA-FCLS 和SGSNMF算法均在泥土丰度图中错误地提取了道路，导致道路无法准确被识别。minimaxNMF 在提取水流端元时不准确，丰度图中出现了道路的轮廓。而其他几种算法均存在无法识别端元，提取精度不纯的问题。此外，如表2 所示，SDGNMF 大多可以获得比其他方法更小的SAD 值，且平均SAD 值最小。上述结果表明，本文提出的算法可以更准确地提取端元，并且获得的丰度图精度高于其他方法。

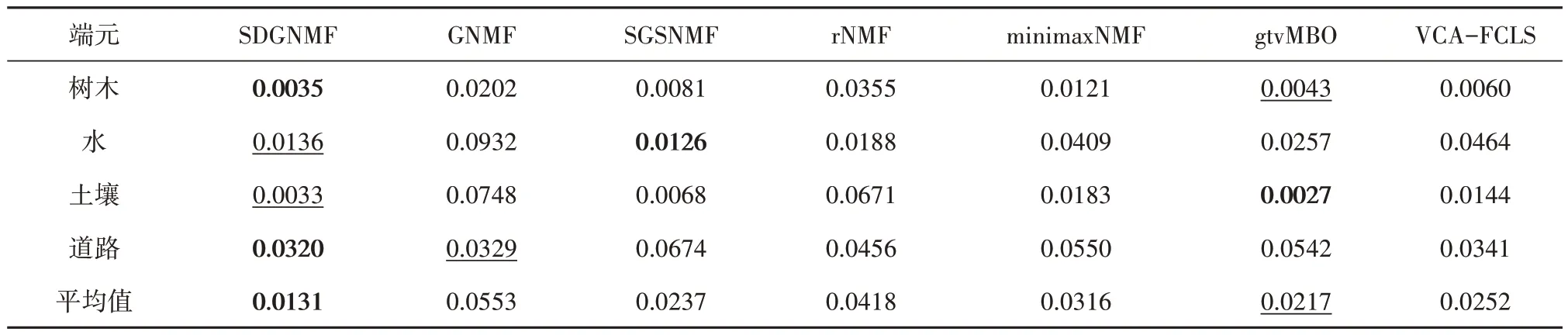
表2 Jasper数据集各算法的SAD对比值Table 2 SAD ratio of algorithms in Jasper dataset

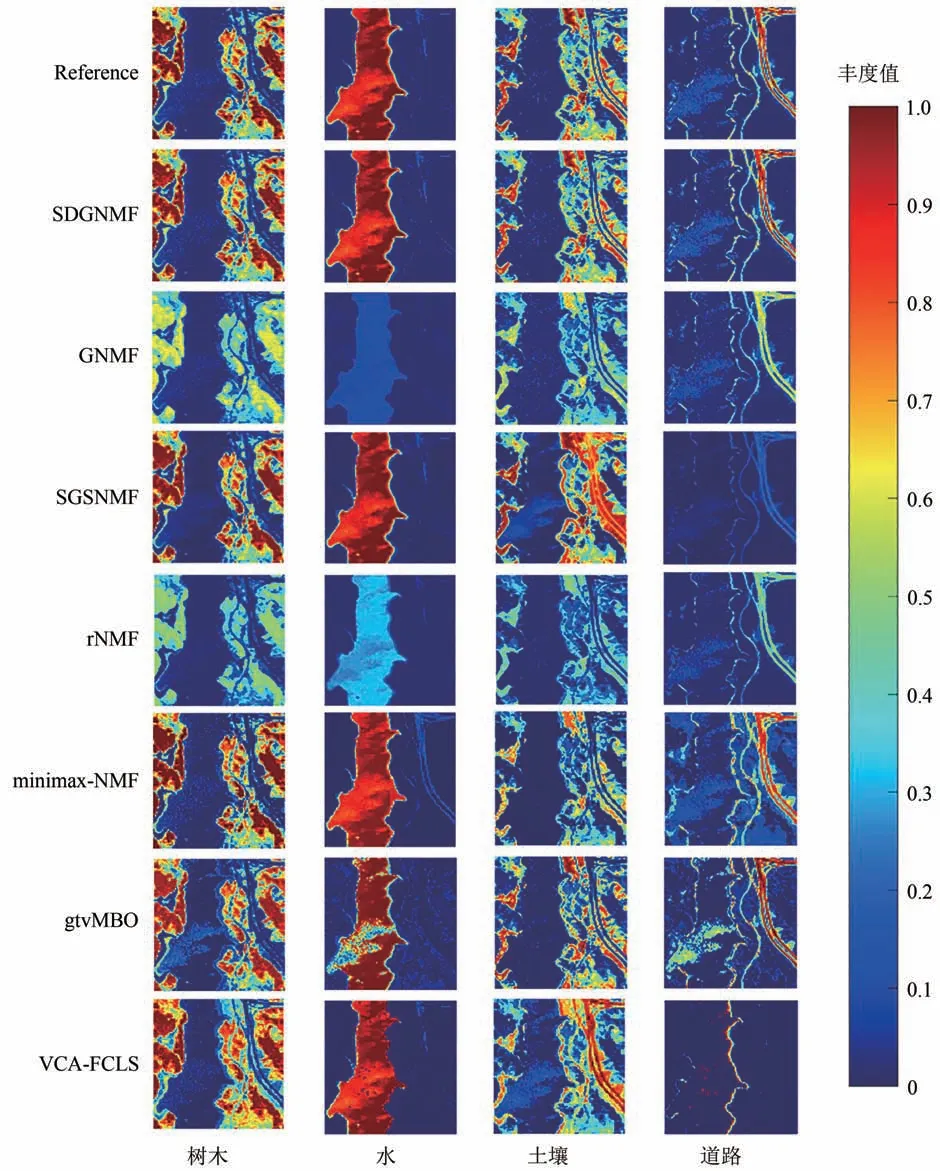
图10 各算法在Jasper数据集上的丰度对比Fig.10 Comparison of abundance maps of each algorithm on Jasper dataset

最后，表3给出了本文算法以及其他几种对比算法在两种真实数据集上的运行时间。尽管根据3.1 节中理论分析可知，本文提出的SDGNMF 相比于EMD，一定程度上减少了时间复杂度。但从表3中可以看出SDGNMF 相对于其他解混算法并不是最节省时间的算法。这是因为SDGNMF 相对于SGSNMF、rNMF、minimaxNMF 这3 种算法，额外引入的图正则项对图的构造付出了很高的计算成本，而对于同样需要构造图的GNMF 和gtvMBO 算法，额外的缩放矩阵迭代求解使得算法迭代次数增大，也在一定程度上降低了计算效率。

表3 真实数据集上各算法运行时间比较Table 3 Runtime of algorithms on real datasets

5 结论

本文提出一种新的光谱解混模型，即SDGNMF。在模拟数据集、Urban 数据集以及Jasper 数据集上的实验结果均表明所提出方法的有效性和优越性。不同于传统解混模型，SDGNMF 模型能够有效克服噪声，并同时考虑特征间的相关性以及数据间的流形结构。与传统的欧氏距离、EMD 相比较，SDGNMF模型采用Sinkhorn距离来度量重构误差具有如下优势：（1）相比于EMD，Sinkhorn距离可以更快速有效地分析高光谱图像中的大规模数据；（2）相比于欧氏距离，Sinkhorn 距离对高光谱数据中的噪声相对不敏感，同时对不同维度上的特征能够分别进行有效建模，特征间的相关性被充分挖掘利用。此外，鉴于SDGNMF 模型的低维表示空间，图正则约束进一步增强了对数据几何流形结构的有效描述。

但是，本文所提出的算法仍然存在计算复杂度较高的问题，因此，后续工作将尝试融合丰度以及端元相关的先验信息于同一框架下，开发更高效的光谱解混算法。