基于纵横向多速度融合的高速列车测速精度研究
2023-12-30赵廷阳
侯 涛, 赵廷阳
(兰州交通大学 自动化与电气工程学院,兰州 730070)
精确测速对确保高速列车安全与高效运行非常重要.目前多数高速列车的运行速度采用多传感器测量,相对位移由列车运行速度积分得到[1].高速列车测速过程受传感器测速误差、车轮磨损、车轮空转及打滑等因素影响,造成速度测量误差偏大,直接影响高速列车的安全与运行效率,进而影响列车节能、自动驾驶等技术的发展.
近年来,国内外专家学者将多传感器融合技术应用到铁路测速系统,通过融合多个传感器的测速来提高高速列车的测速精度与速度控制能力.严建鹏等[2]用自适应算法改进联合卡尔曼滤波对多路传感器测速进行了融合,有效地提高了高速列车的测速精度.Jin 等[3]采用多传感器并行融合滤波方法对列车状态进行估计,该方法能准确估计当前列车的模式和状态.成庶等[4]通过联邦卡尔曼滤波算法优化分配系数,将惯性导航系统、全球卫星导航系统以及多普勒雷达速度传感器有机融合,提高了速度测量的准确性和可靠性,但没有考虑系统噪声对滤波算法的影响.段志强等[5]利用鲁棒滤波器将应答器/SINS 信息融合,对列车位置误差进行了估计,在一定范围内抑制了定位结果的发散,但未考虑有色噪声对陀螺仪的影响.Peng 等[6]提出了一种加速度融合校正和速度累积误差校正的多环卡尔曼滤波融合速度测量与定位算法,测速精度提高了一个数量级,但未考虑卡尔曼滤波器存在的滤波发散问题.Li 等[7]提出了一种基于三级信息融合框架的多源传感器数据融合方法来解决单一数据处理存在的可靠性低、不确定性高的问题,提高了对高速列车运行环境的预测精度.国内外专家学者利用不同的方法将多传感器信息进行融合,获得了相比于单传感器更准确的结果,但存在未考虑系统噪声对滤波算法的影响等问题.
本文在已有研究的基础上,对霍尔速度传感器和雷达速度传感器的测速进行纵横向多速度融合.采用基于衰减记忆法的联邦卡尔曼滤波算法对多路速度进行纵向融合;对纵向多速度融合值进行可靠性判别,确定有效融合值数量;最后采用改进的贝叶斯数据融合算法对有效纵向多速度融合值进行横向多速度融合,进一步提高高速列车的测速精度.
1 高速列车的纵向多速度融合研究
1.1 纵向多速度融合设计
CRH3 系列列车控制系统配备了2 组测速装置,每组测速装置包括一个霍尔速度传感器和一个雷达速度传感器[8].纵向多速度融合是对每路传感器的测速数据进行叠加式采样后,利用基于衰减记忆法的联邦卡尔曼滤波算法进行的多速度融合.图1 是某速度传感器测速的纵向多速度融合示意图.

图1 纵向多速度融合示意图Fig.1 Schematic diagram of the longitudinal multi-speed fusion
当高速列车启动时,4 路速度传感器开始工作.在前3 次测速中,每次取4 路速度传感器中测速的最大值作为列车相应时刻的速度值.从第4 次测速开始,以4 次测速为一个采样周期,对每路速度传感器的测速数据进行采样,然后将采样得到的4 个速度数据进行纵向多速度融合处理,得到的融合值作为对应传感器本次测速值.因除第一次采样外,每一次采样都包含上一次采样中的3 个测速数据,故称作叠加式采样.某速度传感器测速的采样过程示意图如图2 所示,T1、T2、T3为前3 个采样周期,k为采样时刻,N为最大采样时刻.

图2 测速的采样过程示意图Fig.2 Schematic diagram of the sampling process for speed measurement
基于衰减记忆法的联邦卡尔曼滤波结构如图3 所示,由1 个主滤波器和4 个子滤波器构成.子滤波器通过衰减记忆法降低滤波发散的程度,各自进行局部滤波处理并将得到的局部滤波结果送到主滤波器,主滤波器进行时间更新并将局部滤波结果进行融合,从而获得速度的最佳全局估计结果.
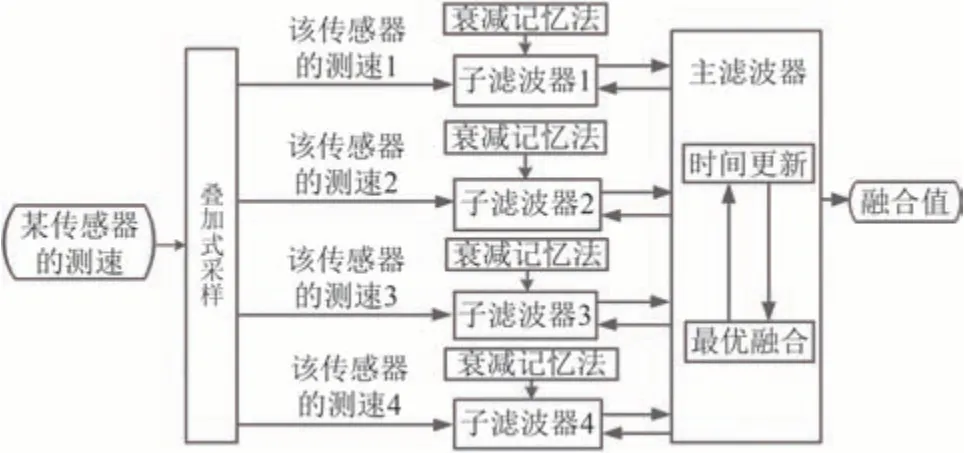
图3 基于衰减记忆法的联邦卡尔曼滤波结构Fig.3 Structure of Federal Kalman filter based on decay memory method
1.2 纵向多速度融合算法
1.2.1 测速系统模型
雷达速度传感器和霍尔速度传感器的输出是离散的高频脉冲信号[9],对脉冲信号进行采样、换算等处理,可得到高速列车的速度数据.结合离散系统的基本特性所建立的测速系统模型为
式中:X(k)与Z(k)分别为系统状态向量与量测向量;V(k)与W(k-1)分别为系统噪声向量与过程噪声向量,都是零均值的高斯白噪声;H(k)与F(k-1)分别为系统的测量矩阵与系统状态转移矩阵.
计算后所获得的噪声统计特性为
式中:j表示第j个采样时刻;Rk为测量噪声协方差矩阵;Qk为状态噪声协方差矩阵;Kronecker 函数[2]为
根据联邦卡尔曼滤波算法原理得到第i(i=1,2,3,4)个子滤波器k时刻的状态方程和量测方程为
初始条件为
式中,(0)与P+(0)分别为在初始时刻的系统状态向量后验估计值和后验估计误差协方差矩阵.
1.2.2 改进的标准卡尔曼滤波算法
联邦卡尔曼滤波中子滤波器采用的是标准卡尔曼滤波算法,它要求已知系统精确的数学模型和噪声统计特性.然而在高速列车运行过程中,噪声信号的特征是未知的,很难得到噪声信号的数学描述,从而导致卡尔曼滤波估计值偏离真实状态,引起滤波发散.衰减记忆法可以使滤波器减小以前量测值的权重,增加最近量测值的权重,提升滤波器对建模误差的鲁棒性.故采用衰减记忆法对标准卡尔曼滤波算法进行改进.
通过最小化E(JN),可以在卡尔曼滤波器中获得先验估计序列.JN为
式中:Rik为第i个子滤波器的测量噪声协方差矩阵;Qik为第i个子滤波器的状态噪声协方差矩阵;(k)为过程噪声估计向量;(k)和(k)通过系统方程相互制约.
卡尔曼滤波器中的JN主要用于说明在当前数据中如何获得最大权值,而衰减记忆卡尔曼滤波器是通过最小化使滤波器最终收敛的状态估计值更接近新的量测数据,的具体定义为
式中:α为衰减因子且α≥1.为使滤波器最终收敛的状态估计值更接近新的量测数据,J͂N的第1 项使当前时刻的协方差最小化[10],此时第2 项为常数.
E()最小化的解与E(JN)最小化的解相似,衰减记忆卡尔曼滤波器中的测量噪声协方差阵相当于α-2k Rik,状态噪声协方差阵相当于α-2k-2Qik.因此,改进后的卡尔曼滤波增益方程为
改进后先验估计误差协方差的时间更新方程为
改进后后验估计误差协方差的量测更新方程为
式中,I为相应维数的单位矩阵.
令
将式(16)和式(17)代入到式(11)、式(13)以及式(15)中,得到
滤波器的更新状态和优化前是相同的,即
利用衰减记忆法,可以解决模型失真造成的滤波发散问题.此外,在用于计算先验估计误差协方差的时间更新方程式(19)的第一项增加α2,相当于在各个子滤波器中增加过程噪声,使滤波器在估计过程中更相信当前测量值.
1.2.3 改进后的联邦卡尔曼滤波融合过程
传感器的测速数据在经过改进的标准卡尔曼滤波处理后得到各自的最优估计(k)和协方差矩阵(k),并被传送到主滤波器,实现各个子滤波器相关数据的融合处理.根据新的增益方程式和协方差更新方程式(18)~式(20),基于衰减记忆法改进的联邦卡尔曼滤波融合过程包括4 个具体步骤.
1) 信息分配.
主滤波器依据信息分配原则向各个子滤波器动态反馈公共观测信息、初始条件信息与噪声信息,信息分配过程为
式中:γi表示信息分配系数;X̂g(k-1)、Pg(k-1)及Qg(k-1)分别表示各子滤波器的局部最优估计值经主滤波器融合后得到的全局最优估计值、误差协方差矩阵及状态噪声协方差矩阵.
Pg(k-1)及Qg(k-1)放大倍后反馈到各个子滤波器,将各子滤波器的估计值重置;同时,主滤波器的误差矩阵重置为全局误差矩阵的倍,即全局误差矩阵调整为(k-1),其中γm≤1. 信息分配满足“信息守恒原则”[11],即
2) 时间更新.
各子滤波器独立地进行时间更新.由式(25)可知,第i个子滤波器的Qik被放大为,也就是说,子滤波器只分配到原状态噪声信息量的一部分,即,此时子滤波器是次优的.但在融合过程中根据“信息守恒原则”过程噪声的信息量能够恢复到原来的值,所以融合后的结果是最优的.时间更新过程为
3) 量测更新.
主滤波器没有量测值,所以主滤波器没有量测更新,量测更新只在各子滤波器中进行.各子滤波器通过最优全局滤波来重置局部滤波值和滤波误差协方差矩阵,即式(23)和式(24),根据时间更新获得的当前时刻状态预测值X̂i(k,k-1)及协方差值P͂-1i(k,k-1)来估计真实值及局部最优误差协方差矩阵,从而完成量测更新.重置后的局部最优滤波误差协方差矩阵为
4)信息融合.
各子滤波器的最优估计及误差协方差矩阵在主滤波器完成全局最优融合,信息融合结果为
式中:P͂+m(k)为主滤波器的误差方差协方差矩阵;X̂m(k)为主滤波器的状态估计值.
2 基于纵向融合值的横向多速度融合
2.1 横向多速度融合设计
为了进一步提高测速精度,采用优化的贝叶斯数据融合算法将纵向融合值进行横向多速度融合,示意图如图4 所示.首先对各路纵向多速度融合值进行可靠性评估,建立置信距离矩阵,以此判断各融合值之间的关系;然后借助模糊数学中映射函数的概念,对置信距离进行判别,删除错误数据;最后采用贝叶斯算法对有效数据进行横向多速度融合.
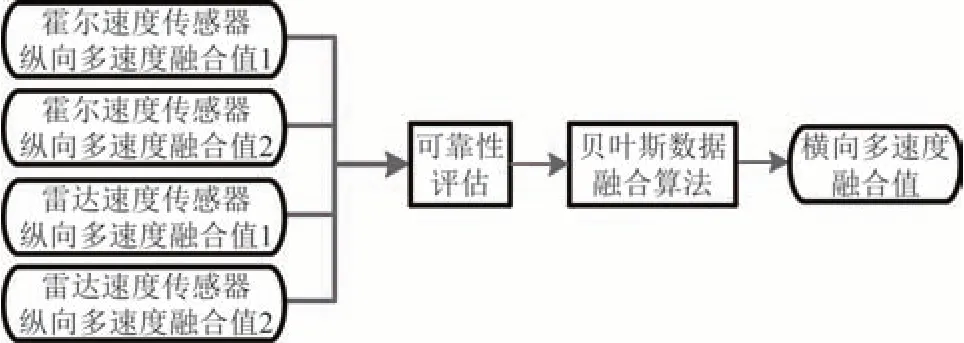
图4 横向多速度融合示意图Fig.4 Schematic diagram of transverse multi-speed fusion
2.2 可靠性评估
纵向多速度融合后,测速精度得到了提高.但是由于故障以及测速环境影响等原因,速度传感器可能提供虚假数据,所以在进行贝叶斯融合前,先对各速度传感器数据进行可靠性评估.
利用多个速度传感器测量列车速度的过程有2 个随机变量:列车的真实速度v,其数值用x表示;每个速度传感器的输出Xa(a=1,2,3,4),用xal表示速度传感器a的第l个测量值,它是随机变量Xa的一次取样.假定同一时刻4 路速度传感器测定的速度都服从正态分布.在真实速度v给定的情况下,传感器输出服从正态分布,均值为μa,标准差设为σa,记为N(μa,).反之,在传感器输出Xa给定的情况下,列车真实速度可以用正态分布来进行表示,记为N(μ0,).基本条件概率密度函数为
定义各数据间的置信距离[12],挑选出更加可靠的传感器数量.用Xa、Xb表示第a个和第b个传感器输出,则一次读数xal和xbl之间的置信距离定义为
由于Xa、Xb满足正态分布,故
式中:pa(x|xal)和pb(x|xbl)分别表示给定xal和xbl时x的条件概率密度函数.
由式(35)~式(38)可知:当xal=xbl时,dab=dba= 0;当xal≫xbl或xal≪xbl时,dab=dba= 1.
计算任意2 个速度传感器之间的置信距离,可得到一个大小为4×4 的置信距离矩阵D,即
利用置信距离对任意2 个传感器之间的可靠程度进行表示,置信距离与传感器之间可靠度成反比关系,当置信距离较小的时候,传感器之间的可靠度较高,相反则较低.
在获得置信距离矩阵后,设定阈值βab来划分置信距离值,以确定2 个传感器是否相互支持.当dab≤βab时,认为来自传感器a和b的测速数据是可靠的,反之认为不可靠.定义判别表达式为
经过可靠性判别之后得到一个二值矩阵,称为关系矩阵S,用来清晰地表示传感器之间的可靠情况,S表示为
2.3 基于优化的贝叶斯算法的横向多速度融合
可靠性评估剔除不可靠数据后,采用贝叶斯数据融合算法对有效纵向融合值进行横向融合.研究表明,贝叶斯理论广泛应用于数据处理领域[13].贝叶斯估计可以充分利用多传感器数据的先验知识,在每次不确定性检测中不断改变参数信息来补偿传感器测量的不稳定性[14].
根据关系矩阵S知,剔除掉不可靠数据后可得n个有效数据xr(r=1,2,…,n),速度传感器的测速参数V的贝叶斯估计值为
式中,P(V|x1,x2,…,xn)是条件概率密度函数,可表示为
设λ=P-1(x1,x2,…,xn),利用贝叶斯公式可得条件概率密度表达式为
式中:μ表示剔除掉不可靠数据后的均值;σr表示剔除掉不可靠数据后的标准差;φ(μ0,σ02)(V)表示测速参数V的条件概率密度函数;φ(μ,σr2)(xr)表示有效数据xr的条件概率密度函数.
由式(44)可知,P(V|x1,x2,…,xn)服从正态分布,假设服从N(μG,σ2G),即
优化后融合速度均值的估计式为
3 仿真验证
使用Matlab 仿真软件,结合霍尔与雷达速度传感器的测速特点,即2 种速度传感器测量误差的标准偏差分别为1.5 m/s 和1.1 m/s,进行测速模拟.考虑高速列车匀速、加速与减速的实际运行,设加速度为0.2 m/s2,减速度为-0.3 m/s2.系统的采样周期和初始值根据实际情况设置,改进前后的联邦卡尔曼滤波算法的基本参数保持一致,信息分配系数选择无反馈模式[15],即γm=0,γi=1/4.
3.1 纵向多速度融合结果及分析
联邦卡尔曼滤波算法进行纵向多速度融合,结果如图5 所示.由图5 可知,单个速度传感器对高速列车测速时,测速值上下波动较大.利用未改进算法进行滤波处理,融合后的速度值上下波动明显减小,整体变化呈相对平稳趋势.经计算,联邦卡尔曼滤波算法结果的平均误差是1.333 6 km/h.
图6 为运用衰减记忆法改进联邦卡尔曼滤波算法的纵向多速度融合结果.与未改进算法的结果对比发现,改进后的滤波结果更平稳,精确度更高.经计算,改进后算法结果的平均误差是0.669 6 km/h,与联邦卡尔曼滤波算法相比误差减小40.9%,较大程度抑制了滤波发散问题.

图6 基于衰减记忆法的联邦卡尔曼滤波算法融合结果Fig.6 Results of Federal Kalman filtering algorithm based on decay memory method
3.2 横向多速度融合结果及分析
以某时刻高速列车纵向多速度融合数据为样本,根据式(39)对速度传感器之间的置信距离进行计算,获得置信距离矩阵为
选择阈值βab=0.01,则对应的关系矩阵为
从置信距离矩阵以及对应的关系矩阵可以看出,每个置信距离值都比较小,所以认定4 个传感器之间相互支持,不存在故障数据.
采用优化前后的贝叶斯数据融合方法,分别对4 路纵向融合速度值再进行横向融合,误差对比结果如图7 所示.在仿真时间0~100 s 内,与列车实际运行速度相比,未优化的贝叶斯速度融合平均误差为0.496 8 km/h,优化后的贝叶斯速度融合平均误差为0.224 8 km/h,优化后误差减少了54.8%.

图7 优化前后的贝叶斯速度融合误差对比Fig.7 Comparison of Bayesian speed fusion errors before and after optimization
图8 是对多个传感器测速的纵横向多速度融合的对比结果.由图8 可知,经过“纵向+横向”融合后,速度融合值更加平稳,精度更高.经过计算,融合后速度误差对比情况如图9 所示.在仿真时间内,纵横向多速度融合效果更好,与列车实际运行速度相比,平均误差为0.392 8 km/h, 与改进后的纵向多速度融合滤波算法平均误差0.669 6 km/h 相比,误差减小了41.3%, 融合精度更高.
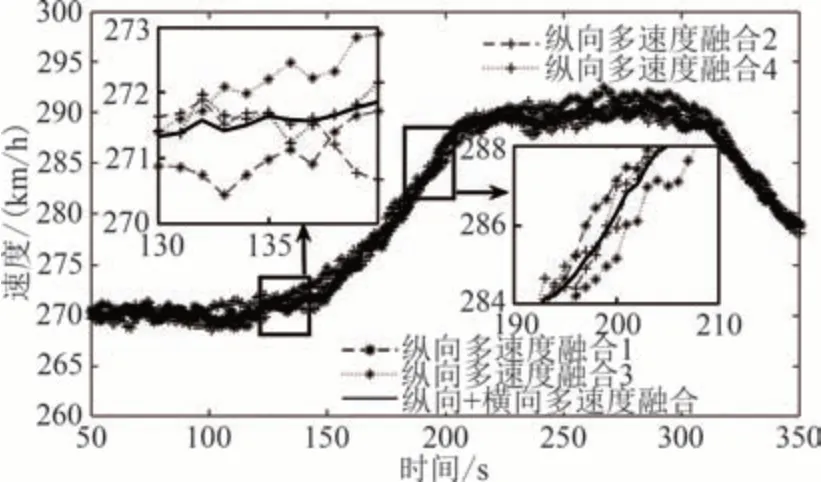
图8 纵横向多速度融合结果Fig.8 Results of longitudinal and transverse multi-speed fusion
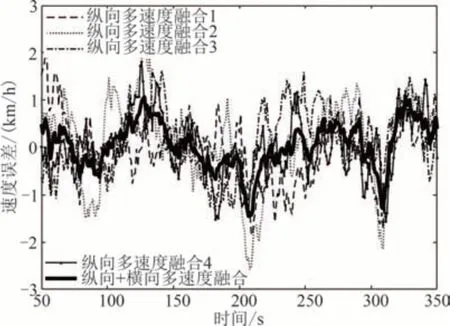
图9 融合速度误差对比Fig.9 Comparison of fusion speed errors
4 结论
1)提出的基于衰减记忆法的联邦卡尔曼滤波算法的融合速度平均误差为0.669 6 km/h,与未改进算法相比误差减小了40.9 %,较大程度解决了滤波发散问题,融合结果更加精确.
2)在进行横向多速度融合前,通过可靠性评估确定速度传感器测速的有效融合数量,排除了传感器故障影响,保证了横向多速度融合的准确性.
3)提出的纵向+横向多速度融合测速方法,测速的平均误差为0.392 8 km/h,与改进后的纵向多速度融合滤波算法平均误差0.669 6 km/h 相比,误差减小了41.3%,平均测速精度有较大的提升,对高速列车精确测速工作具有一定的实际参考意义.
