给空间观念培养创造足够的空间

人类生活在“空间”的世界，对空间的认知是人们认识世界、适应周围环境必备的前提，而这种认知需要空间观念作为保障。建立好空间观念，一方面，可以帮助学生更好地探索和利用我们生活的空间；另一方面，空间观念是创新精神的基本要素，对培养人的创新精神和实践能力起着至关重要的作用。

一、学情分析

1.调研对象：垂杨柳中心小学已学过长方体、正方体内容的30名学生。

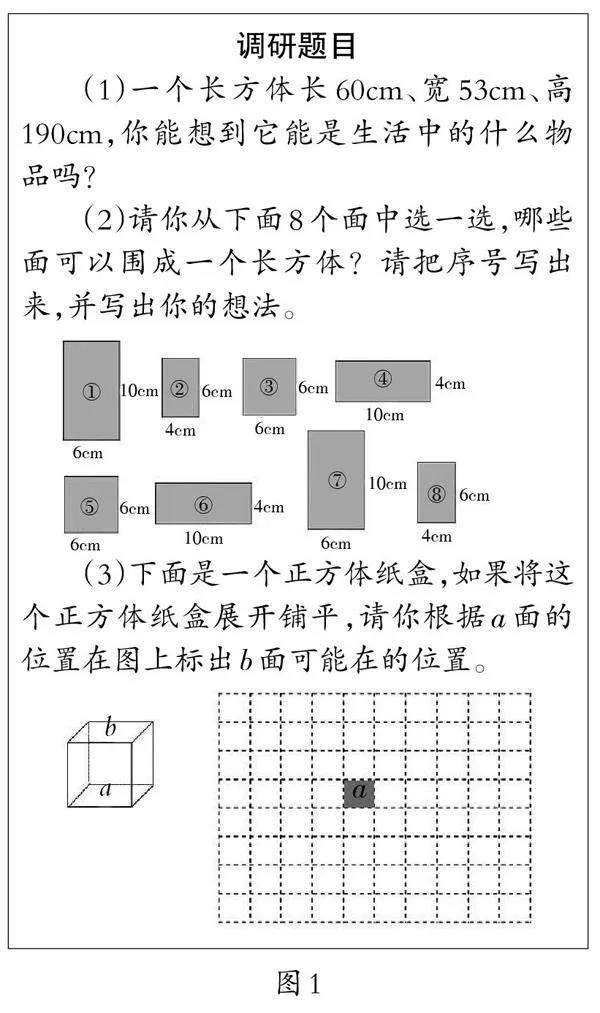
2.调研题目（如图1）。

3.调研说明及结果。

三道调研题目意在从三维图形形状和大小的想象、二维转化为三维图形的想象、三维转化为二维图形的想象这三个方面对学生进行调研分析。

第（1）题调研结果为：答案符合生活实际的（如冰箱）有17人（占56.7%），不符合实际的（如课桌）有13人。

近一半的学生根据数据想象物体大小以及根据几何图形想象出所描述的实际物体还是存在很大障碍的，说明这部分学生基于一维元素对所构成的三维图形的形状、大小的想象力不足。

第（2）题调研结果为：确定面数正确的占87%，选面正确的占58%。这反映出大部分学生可以借助长方体面的特点进行选择，但是仍有很多学生对于长方体面与面之间位置关系，特别是相邻面之间位置关系的想象力比较匮乏。

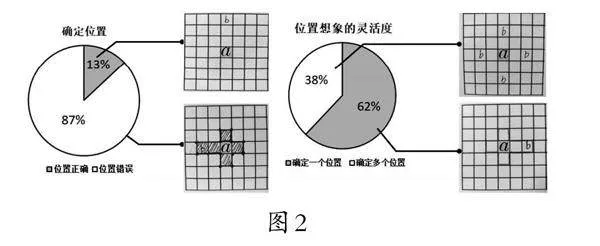
第（3）题的调研结果如图2。

有26人能够正确确定b面所在的位置，说明学生在三维转化为二维的过程中根据一个面想象对面的位置并不困难。但是在这26人中，仅有10人能够确定b面可能在多个位置。这说明学生基于前面的学习具备了能够完成连续、多个面图形变化的空间想象，但是仍然缺乏空间多角度想象能力。他们需要进一步培养空间观念、丰富空间想象能力。

通过这三道题的数据分析，可以看出学生在认识长方体和正方体的面、棱、顶点这些组成元素特点后，还需要插上一双想象的翅膀。不仅要根据组成元素的特点对长方体、正方体的大小、形状进行想象，还要在三维与二维空间的双向转化中对组成元素之间的位置关系进行想象，以此来增强学生空间想象的丰富性。

设计怎样的活动能够帮助学生克服维度间转化的困难，培养空间观念、发展空间想象力呢？我想可以从两个方面着力：第一，通过一维想象三维，培养学生对图形形状、大小空间想象的同时促使学生感受一维元素在图形构造中的核心作用；第二，增加由三维向二维图形转化素材，培养学生对图形元素位置关系的想象的同时增强学生对空间的多角度想象能力。

培养空间观念的主要方式是观察、想象、操作，在具体教学过程中，可以借助以下三课时的主题活动发展学生空间观念、培养空间想象力。

二、教学活动设计

第一课时：对长方体、正方体形状、大小的想象——基于一维元素大小对三维图形的大小、形状展开想象。

首先为学生创设用形状、大小不同的整理箱来整理家里散乱物品的情境，随后通过三个想象活动引导学生在观察中想象。

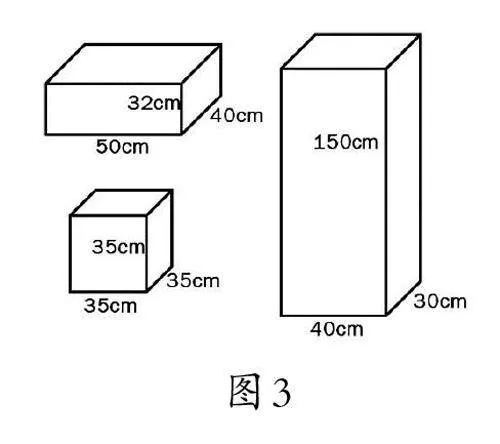
活动（一）：对大小的想象。为学生出示给定棱长数据的长方体、正方体几何图形，引导学生根据棱长数据对整理箱大小进行想象。（如图3）

活动（二）：对形状的想象。在黑板上画出长方体整理箱的透视图，然后引导学生思考：一定要把这12条棱都画全了才能想到这个长方体整理箱的形状吗？最少留几条棱依然能让我们想到它的形状？学生在擦除棱的过程中逐渐明确，只要剩下一组长、宽、高仍然可以想象出长方体的形状。

活动（三）：对形状和大小同时想象。只出示长方体和正方体的棱长数据，引导学生想象：它可能是我们生活中的什么东西？学生会说：它是冰箱、手机、魔方等。

（1）一个长方体长14cm、宽6.5cm、高0.5cm。

（2）一个长方体长60cm、宽53cm、高190cm。

（3）一个正方体棱长9cm。

【设计意图】三个活动的设计不仅培养学生对长方体、正方体的形状、大小的想象能力，还让学生深刻地体会到棱是长方体、正方体特征的核心要素，一维棱的大小既决定二维面的大小，也决定三维体的大小。同时为第二课时对元素之间位置关系的想象做好了思维上的铺垫。

第二课时：引导学生在二维向三维建构过程中展开想象。

首先，创设一个为乐高小屋设计合适大小整理箱的问题情境，在这样的情境下分两个活动展开。（如图4）

（一）选面拼体。

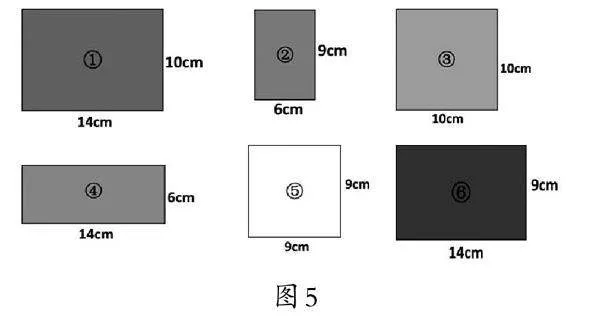
为学生提供六种规格的纸板（如图5），学生通过小组合作选择纸板并完成计划单。通过选择纸板激发学生由二维向三维建构的想象。选好纸板后学生开始制作，如果在制作的过程中学生发现自己选的纸板不合适，就要先填写修改单，然后拿着修改单找老师更换纸板。

在汇报环节主要有以下这三种情况：

（1）选错了面围不出长方体。

（2）选对了面围出了长方体，但是大小不合适，不能装下乐高小屋。

（3）选对了面围出了长方体且能够装下乐高小屋。

【设计意图】借助前两种情况组织学生研讨，在反思和交流中使学生逐渐明确长方体相邻面、相对面位置关系的特点，也体会到全面考虑问题的重要性。第三种情况是一次性成功的，借助这组学生的经验分享，促使全班学生明确借助长、宽、高三条棱对面与面之间位置关系的想象方法。

（二）选面折体。

为学生提供4个长方体整理箱的展开图（图略），引导学生观察想象：哪个展开图可以折出长方体整理箱？学生在选出③号图之后，接着固定一个面为底面引导学生想象：折成长方体后哪个面和它相对？哪些面和它是相邻的？然后学生借助学具折出长方体，验证自己的想象。

【设计意图】学生在选面拼体和选面折体的两次活动中，经历由二维向三维建构的过程，使学生对长方体形状以及面与面位置关系的想象更丰富，为下节课正方体的解构奠定一定思维基础。

第三课时：引导学生在三维向二维的解构过程中展开想象。

创设情境：为正方体磁力魔方设计整理盒。主要是两次剪展开图的活动。

第一次，沿棱随意剪。学生相互完善补充，展示剪出的11种展开图（图略）。这时引发学生思考：展开图的形状不同，但是剪的过程中有什么相同的地方？学生就会关注到这11种情况均剪开了7条棱。这时我顺势追问：怎么都剪开7条棱呢？有学生说：总共减去剩下的。还有学生说：将周长所包含的棱数除以2得到剪开7条棱。学生通过想象和推理给出两种解释。

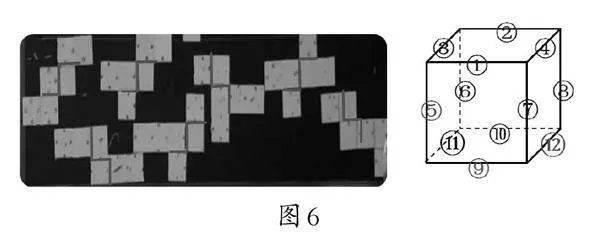
第二次，定棱有意剪。在第一次随意剪的基础上为学生提出更高的要求：如果⑤号、⑨号和 [12]号棱不剪开，那么怎样剪就可以剪出正方体展开图？在操作前请大家先想一想，把你觉得要剪的棱的序号写下来！

按要求剪出展开图后，引导学生进一步观察、思考：剪出的展开图有什么共同的特征？学生惊讶地发现，在符合要求的展开图中都有个Z图案。而之所以产生Z图案，是因为这3条棱的位置关系。（如图6）

这时学生的思维已经处于非常活跃的状态，我抓住机会继续推波助澜，再次追问：如果⑨号、 [12]号和⑦号棱不剪开，还能剪出正方体展开图吗？为什么？学生很快就想到了，如果这3条棱不剪开，就铺不平，无法剪出展开图，因为这3条棱是相交于一个顶点的。

【设计意图】两次剪，使学生经历由三维向二维的解构过程，也完成由感性到理性的升华，将学生空间想象推向丰富、深刻的高阶思维阶段。三课时的活动带领学生经历在观察、操作、推理中想象，不仅培养学生的空间想象能力，而且在学生的思维中埋下实践创新的种子。