构建结构化教学体系，促进学生认知结构发展

2022年版课标指出：数学课程内容的一大特点就是整体性和一致性。在数的运算中，从运算意义的角度来看，加、减、乘、除本质上是一个整体，但学生对其中的联系十分模糊，这会导致学生产生只知算法、不问算理的情况。本文以“两位数除以一位数（最高位不能整除）”为例，从现有整数除法运算教学中的错误现象、原因分析及改进策略三个方面谈谈如何把握除法运算的整体性和一致性。

一、错误现象

在整数除法的学习过程中，以下几个问题屡见不鲜。

现象一：商的最高位位置有误。在教学反馈中，发现一些学生在计算中把商的最高位写错位置。如计算57÷18，商的最高位3应写在个位上和被除数中的7对齐，实际却错写在了十位上和被除数中的5对齐。

现象二：商中间的“0”漏写。经常见到有学生无法理解“不够商1用0占位”的道理。如计算735÷7，商应是105，学生却漏写了0，得出错误结果15。

现象三：忽略余数与除数的关系。在学习最高位不够除后受“一位不够看两位”思维定式的影响出现错误。如计算423÷3，学生会出现用42÷3直接在商的十位上写9的现象，忽略了余数应比除数小的算理。又如：学生会出现48400÷900=53……7的错误，这是因为没能清楚这里的余数7表示的应是7个百。

二、原因分析

为什么多数学生一遇除法错误率就高了呢？究其原因如下：

1.除法竖式格式较为特殊。从算式的竖式结构看：加法、减法和乘法是一致的，在学习了加法竖式后，减法和乘法的竖式容易纳入已有的认知结构而被学生接受，而除法竖式较为特殊，跟加法、减法和乘法的不一样，导致学生不容易接受。如有学生在列竖式时更多的是记忆与模仿，不能结合算理理解每一步运算表示的意义，导致列竖式的格式和计算结果都是错的。

2.除法运算过程多样。从运算过程来看，加法和减法只含有加或减一种运算，乘法含两种，即乘法和加法，而除法含有加、减、乘多种运算，每一步运算都有其特定的含义，如果不能理解其中的意义，运算过程中就容易出错，这无疑增加了除法运算的难度。

3.试商思考过程复杂。从思考的过程来看，除法运算包含估、定、试、比、调、判断等思考过程。即首先必须估计商的取值范围，接着要确定商的位置，再用确定的商试商，接着进行余数与除数的大小比较，最后来调整商的大小。有时还要判断结果能不能除尽，整个思考过程极其复杂。尤其是除数是两位数的除法，需要不断地试商、调商，学生的计算速度和准确率明显下降。

综上，造成上述问题的根本原因是学生对除法运算的算理与算法形成割裂，没有形成结构化的认知体系。主要表现在：一是对整数除法运算的算理理解不到位，没有深刻理解从高位除起，被除数被分解成以不同计数单位为单位的若干个部分，用这些部分分别除以除数，将除法运算还原成乘法口诀表中的乘法运算进行试商；二是对算法的掌握还停留在记忆模仿中，导致学生不能根据实际情况准确判断除法运算的类型，更不能灵活运用除法运算的方法进行计算；三是口算不扎实。要保证笔算的正确率和运算速度，口算是关键，其中表内乘法和20以内的加减法是基础中的基础，必须让学生熟练掌握。

三、改进策略

小学生仍然以直观形象思维为主，而算理、算法又十分抽象，因此如何结合学生的思维特点处理好除法运算教学中算理与算法的关系，往往就是教学的难点所在。我们可以结合学生的年龄特点，借助生动有趣的生活情境、借助直观模型、借助学生已有的认知基础和生活经验，引导学生准确理解除法运算的意义，促进算法与算理融会贯通，从而让学生充分感悟算法和算理的一致性。笔者认为把握好整数除法运算中如下几个层次的教学尤为重要。

1.在直观操作中，感悟算法和算理的一致性。

环节一：69÷3（最高位能整除）。

提问：你想怎样计算69÷3？

交流：可以分小棒、口算、列竖式。

追问：这几种方法之间有什么联系？

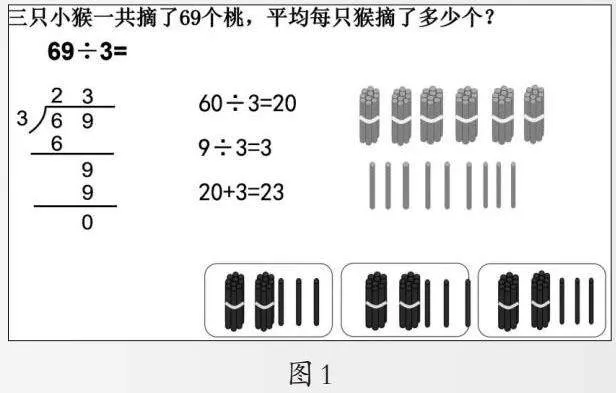
课始借助情境出示计算69÷3，引导学生回顾上节课最高位能整除的知识。交流分小棒表示69÷3的过程，用横式对应表示出每一步的操作过程，如分6捆的过程，想乘法口诀二三得六表示为60÷3=20，分9根的过程表示为9÷3=3。如何列竖式表示分小棒的过程是除法笔算的难点之一，特别是把6捆平均分成3份的结果2为什么写在商的最高位。可通过引导学生讨论解决该难点：因为这是与60÷3=20相对应的，所以2表示2个十。从而让学生初步感悟笔算除法时，除到被除数的哪一位商就要写在哪一位上，这是和先分哪一个计数单位上的数相对应的。再通过引导比较分小棒、口算、列竖式这三种方法的联系（如图1），从而引导学生发现口算记录了分小棒的过程，而笔算（列竖式）则更为简洁地记录了口算的过程。各环节环环相扣，促使学生对算法和算理的理解走向一致。

环节二：78÷3（最高位不能整除）。

提问：78÷3和69÷3有什么不同之处？如何计算？

思考：为什么只分6捆？余下的1捆怎么办？

追问：这几种计算方法之间有什么联系？

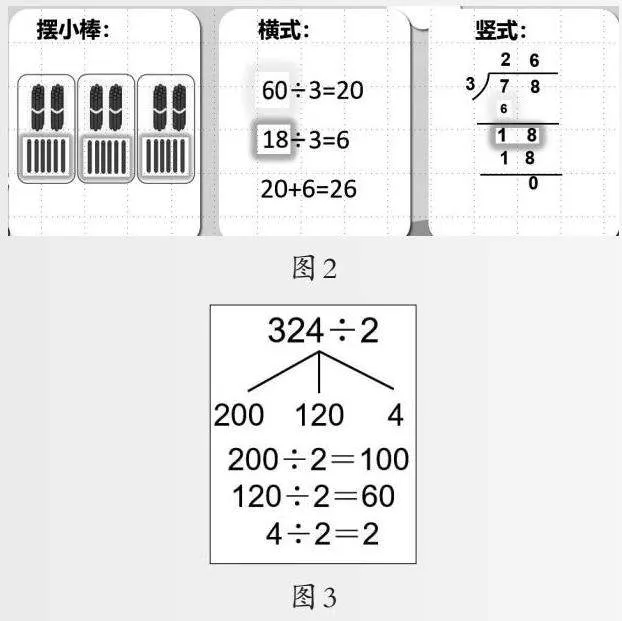
比较发现：69÷3中的6捆全部分完，每份都能得到整捆。78÷3，用分一分的方法发现，需要把7个十平均分3份，根据乘法口诀二三得六，每份最多只能得到2个十。那就在7捆里先拿出6捆平均分成3份，每份就能分得2捆，剩下的1捆拆成10根和8根合起来再平均分。像这样被除数最高位不能整除的，通过再次分小棒，学生感受到利用表内乘法口诀，只要找到最高位最多有几个整捆能平均分，拆分剩下的整捆小棒和下一位表示的几根小棒合起来继续平均分。从“最高位能整除”的三种方法迁移到“最高位不能整除”，再次同屏比较发现（如图2），虽然最高位不能全部分完产生了余数，但是除法计算过程中都是细分计数单位个数的算理是不变的，体现了“最高位能整除”和“最高位不能整除”的算法和算理的一致性。

以此类推，学生的认知结构会形成不管被除数是几位数，只要从最高位开始找到每一个数位里有几个除数，结合乘和减的运算就能顺利解决除数是一位数的除法。

2.在迁移类推中，感悟除法运算的整体性。

环节三：324÷2（最高位不能整除）。

提问：如果百位除后有余数怎么办？

思考：借助方块模型如何分？

追问：如果千位除后有余数怎么办？

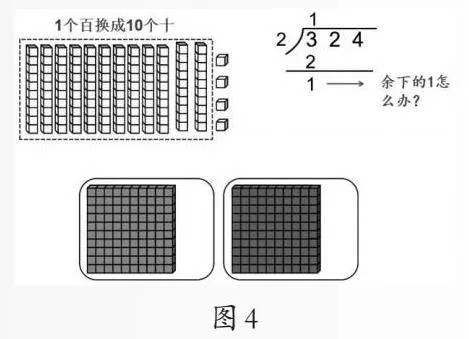
在教学中设计问题情境，提出问题：324÷2等于多少？没有324根小棒怎么办？学生会产生拆计数单位的想法，出现如图3所示的口算过程。如何进行竖式计算仍然是学生理解的难点之一。还需借助实际操作促进直观理解，引导学生设想头脑中有3大捆小棒（1大捆代表1个百），也可以借助小方块图分一分、连一连。在分的过程中出现类似环节二不能整分的情况，学生会轻松想到拆分1大捆。启发思考：用竖式计算324÷2，百位上余“1”该怎么办呢？结合动画演示让学生再次感受最高位最多有几个整百能平均分，拆分余下的1个百和下一位几个十合起来继续平均分，以此类推，一直分到个位结束（如图4）。这样才能形成对竖式计算的结构化认知。接着进行拓展：如果被除数是四位数，千位除后有余数怎么办？学生的学习经验会在图3的基础上不断叠加，逐步感受到不管被除数是几位数，只要从最高位开始找到每一个数位里有几个除数，把余下的数和下一个数位上的数合起来平均分，一直这样平均分到个位为止。

环节四：136÷2（最高位不够除）。

提问：被除数的最高位发生了什么变化？

思考：该怎样用竖式表示分小棒的过程？

这个算式的出示再次逼近学生的最近发展区。被除数最高位比除数小，与已有的认知发生冲突。1个百平均分成2份，商的最高位无法得到1个百。问题驱动会激发学生自主探究，如果和下一位十位上的数合起来就会得到13个十，比除数2大，就能够进行平均分，从而得到6个十；剩余的1个十再转化成10个一，接着平均分成2份，每份得到8个一。用横式表示算理的方法为：13（十）÷2=6（十）……1（十）；16（个）÷2=8（个）。最后将所有的商6（十）与8（个）组合起来，得到结果68。像这样最高位不够除，一位不够看两位，用第二位的计数单位来均分，每次的余数只要比除数小，就可以转化成下一个计数单位的个数继续平均分，从而实现“最高位不够除”和“最高位够除”的算理和算法的有机统一。

综上所述，整数除法运算的整体性和一致性体现为：都是计数单位与计数单位相除，计数单位的个数与计数单位的个数相除。掌握了除数是一位数的除法算理和算法后，对于除数是两、三位数的除法运算，只是除数变成几十、几百，被除数仍然被分解成以不同计数单位为单位的若干个部分，分别除以除数，只需熟练掌握试商和调商的技能技巧就能顺利解决问题。基于算理、算法的一致性，后续学习探索小数、分数的计算方法和算理时，要联系整数除法运算的算理和算法进行合理迁移类推，在联系中感悟数的运算以及运算之间的关系，体会数的运算的一致性，从而发展学生对数的运算认知结构的理解。

（作者单位：南京师范大学苏州实验学校）