着眼“理趣”，遇见美好

对于不少学生来说，他们相信数学学习是美好的事情吗？美好的数学学习体验真的即将发生在他们身上吗？答案很可能还是个问号。笔者认为，着眼数学学习的“理趣”，可以让学生在数学课堂上遇见美好。下面以“认识三角形”一课的教学片段为例，谈谈笔者的实践与思考。

片段一：聚焦概念本质，在问题情境中激“趣”诱“理”

师：中央电视台有一档互动求证类节目——《是真的吗》，你们看过吗？老师给大家带来其中一个片段，想不想看？

课件播放《是真的吗》片段：有网友说，用三根火柴棍就能把瓶装水吊在桌边，是真的吗？

师：怎么样，没想到吧？感兴趣的同学可以试着做这个实验，看看最多能吊几瓶水。数学中有很多问题，也需要我们用“是真的吗”的质疑精神去探究，只要敢想会想，一定会有更多的收获。

师：其实，刚才的实验用到了一个我们认识的平面图形，看出来了吗？你能举几个生活中三角形的例子吗？

生：自行车的车架是三角形的。

生：我们天天戴的红领巾也是三角形的。

师：看来，生活中的三角形还真不少，这些三角形长得都一样吗？它们有什么不同？

生：这些三角形的形状不相同。

生：它们的大小也不相同。

师：既然它们的形状、大小都不相同，为什么你们都认为它们是三角形呢？

生：因为它们都有3条边、3个角、3个顶点。

师：尽管三角形都有3个顶点、3条边和3个角，但它们的形状和大小不一定相同。那么，三角形的顶点、边以及角对三角形的形状和大小起多大的决定性作用呢？想不想来一组“是真的吗”数学实验，一探究竟？

课件依次出示如下问题：

1.3个顶点的位置确定了，三角形的形状和大小就确定了。是真的吗？

2.3个角的大小确定了，三角形的形状和大小就确定了。是真的吗？

3.3条边的长短确定了，三角形的形状和大小就确定了。是真的吗？

学生先自主研究，再在小组内交流自己的想法，指名全班汇报。

生：我先在纸上随便点3个点，然后用线段把它们连起来，我发现只要3个点的位置定下来了，三角形的形状和大小就定下来了，所以第一句话是真的。

师：在纸上随意（加重语气）点3个点，一定能围成一个三角形吗？

生：只要这3个点不在同一条直线上就行。

生：我比较了老师的大三角板和我的小三角板，虽然它们3个角的度数是相等的，形状也是一样的，但是它们的大小并不相同，所以三角形角的大小确定了，三角形的形状能够确定，三角形的大小却不能确定。

生：我用3根小棒围三角形，不管3根小棒的位置怎么摆放，最后围出的三角形都是同一个，所以三角形边的长短确定了，三角形的形状和大小就确定了，这句话是真的。

【思考】课始，以学生都很感兴趣的电视节目《是真的吗》引入，既很好地调动了学生的好奇心，营造出想进一步探究的积极氛围，又巧妙地引出这节课要深入研究的主角——三角形，也为后续以三角形中的“是真的吗”为研究主题做好了铺垫。三个关于顶点、边和角的“是真的吗”问题，为学生的进一步探究指明了目标，从“是真的吗”延伸开来的问题情境之“趣”，引发儿童向探究三角形特征内在之“理”进发。

片段二：经历发现过程，在操作活动中借“趣”明“理”

师：刚才我们通过一组“是真的吗”数学实验，理解了三角形的定义。还想继续挑战吗？

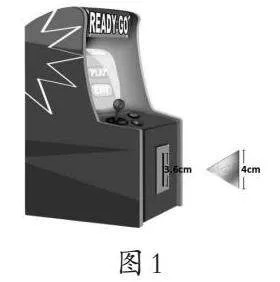
课件出示：一种游戏机投币口的高度为3.6cm，一种3条边都相等的三角形游戏币，边长为4cm。（如图1）

师：你们觉得这个游戏币能从投币口投进去吗？

生：（异口同声）不能。

课件演示游戏币卡在投币口的动画。然后出示问题：有网友说，这种游戏币能从投币口投进去。是真的吗？

多数学生坚持认为不可能，少数学生犹豫不决。

师：到底可不可能，实验让我们眼见为实。

学生小组活动，尝试将边长4cm的正三角形塑料片（代替游戏币）投入投币口高度为3.6cm的储蓄罐（代替游戏机）。指名上台演示投币过程。

师：的确，如果将三角形的一条边平着从投币口往里塞，游戏币就能通过投币口。你能试着在游戏币上画出三角形通过投币口时需要的最小高度吗？

学生在研究单上尝试画三角形游戏币的高，教师指名交流画法。

师：你是怎么画出这条最小高度的线段的？

生：从三角形上面的顶点往下面那条边作垂线，这条垂直线段就是从上面的顶点到下面的边中最短的一条线段。

师：真厉害！你们所画出的这条垂直线段，数学上专门给它取了一个名字，让我们一起看课件。

课件揭示三角形底和高的定义：从三角形的一个顶点到对边的垂直线段是三角形的高，这条对边是三角形的底。

【思考】本环节巧妙借助游戏机投币的活动情境，制造学生的认知冲突，再让学生通过自己的尝试操作，获得投币成功后既愉悦又疑惑的真切感受。在这样双重感受的作用下，学生一定很想研究出三角形游戏币成功通过投币口的秘诀，从而把那条隐藏着的“高”找出来。数学上的“高”与生活中的“高”在这里得到了有效联结和转换，学生也在这样充满探究气息的操作活动中借“趣”明“理”。

片段三：解决实际问题，在运用拓展中循“趣”究“理”

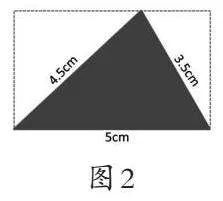
出示问题：小明用长方形卡纸做一个三角形贺卡（如图2）。做成的贺卡3条边的长度分别是5cm、4.5cm、3.5cm，原长方形卡纸的长是5cm，原卡纸的宽至少要多少厘米？

生1：我觉得原来卡纸的宽至少要3.5cm。

生2：我觉得原来卡纸的宽可以比3.5cm短，只要画出5cm那条边上的高，就能量出来。

师：你们听懂他的意思了吗？为什么要画出那条高呢？

生2：因为高是三角形的一个顶点到对边的最短线段，长方形卡纸的宽只要不比这条高短就够了。

教师肯定生2的想法后，课件出示：有网友说，长方形卡纸的宽度只要3cm左右就够了，是真的吗？

学生在研究单上画一画，量一量，找出原长方形卡纸的最小宽度。然后教师指名交流画法和想法。

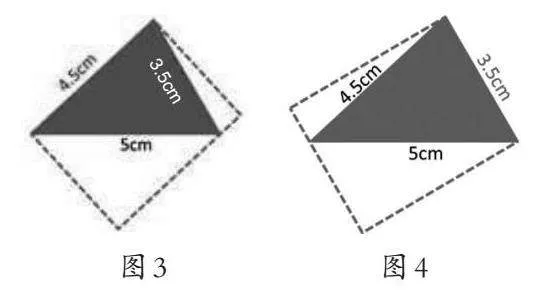
师：让我们换个方向做贺卡。如果给你一张长4.5cm的长方形卡纸（如图3），或者给你一张宽3.5cm的长方形卡纸（如图4），你能在三角形中画出长方形卡纸最短的宽（或长）吗？

学生继续尝试画高，并在组内交流自己的发现，教师指名汇报想法。

师总结：三角形有3个顶点、3条边，从每一个顶点往它的对边作垂线，都能得到1条高。所以三角形有几条高？

生：（齐）3条高。

师：三角形的每一组底和高都是互相——

生：（齐）垂直的。

师：（神秘地）如果在同一个三角形里把这3条高都画出来，你还会有惊喜的发现呢，同学们课后不妨试一试。

【思考】本环节教师闭口不提让学生画高，而是继续创设新颖有趣的问题情境，让学生在对现实问题进行分析和思考的基础上循“趣”究“理”，主动发现隐藏其中的三角形的高是解决问题的关键。正因为画出三角形的高是解决现实问题的迫切需要，学生画高的动力才会更加充沛。在学生初次通过画高顺利解决问题之后，教师改变卡纸的方向，带领学生继续思考新的问题，引导学生发现三角形高的条数特点，并为三角形的3条高相交于一点埋下伏笔。学生在这样的灵活运用和不断拓展的过程中，思维水平不断攀升，对知识的理解也逐渐变得清晰通透。

片段四：着眼思维生长，在总结反思中点“趣”亮“理”

师：今天这节课我们一起进一步认识了三角形，通过今天的学习，你们有哪些新的收获？

生答略。

师总结：同学们的收获还真不少！今天这节课我们借助“是真的吗”数学实验，研究了很多关于三角形的数学问题。不过，很多问题都是网友提出来的，你们能像爱思考的网友一样，提出更多、更有意思的关于三角形的问题吗？

学生小组讨论，然后教师指名交流汇报。

生：锐角三角形和直角三角形的高我们会画了，钝角三角形的高应该怎么画呢？

生：锐角三角形有3条高，那是不是所有三角形都有3条高呢？

生：我们知道，长方形的长和宽确定了，长方形的大小和形状也就确定了。那三角形的底和高确定了，三角形的形状和大小是不是也确定了呢？

师：同学们非常会思考、会提问！感兴趣的同学课后可以继续研究大家提出来的这些问题。只要我们用“是真的吗”这样一种刨根问底的精神去探究，相信大家一定能找到这些问题的答案。

【思考】在课的最后，在学生通过本节课的学习，初步积累了一定的关于三角形的知识和经验的基础上，教师引导学生进行课堂总结和反思，并围绕课堂所学、结合自己感兴趣的问题进行有针对性的提问，鼓励学生继续用“是真的吗”这种刨根问底的精神去探究。学生提出的那一个个思路清晰并且独具个性的问题，犹如为他们的后续学习点亮一盏盏指路明灯，引领着他们朝着理趣共生的美好学习之境迈进。

（作者单位：江苏南通市八一小学）