创设结构化题组 突出对比性训练

平常我们在设计正比例和反比例解决问题的练习时，会想到以题组的方式组织学生训练。但设计怎样的题组既能使学生进一步认识到在同一个数量关系下正比例和反比例问题的变化结构，又能通过不同形式的对比性练习，提高分析问题和解决问题的能力呢？为此，我们针对这节综合练习课做了实践研究。

一、揭示数量关系，勾起概念回忆

师：在日常生活中经常会碰到两个相关联的量成正比例或成反比例关系，那怎样的两个相关联的量成正比例？怎样的两个相关联的量成反比例？

教师结合学生的回答相机板书正比例和反比例的数量关系式。

师：你们针对“单价×数量＝总价”这个具体数量关系来说一说，在怎样的情况下两个相关联的量成正比例或成反比例？

生：当总价一定时，单价和数量成反比例；当单价一定时，总价和数量成正比例；当数量一定时，总价和单价成正比例。

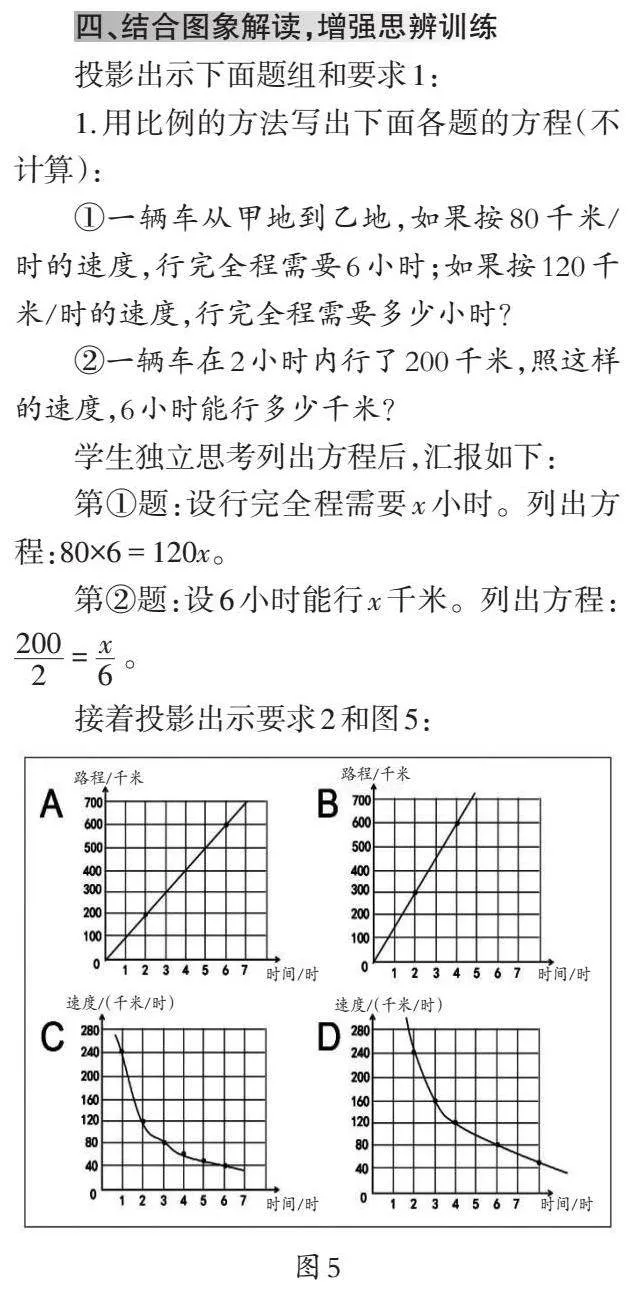
教师针对学生的回答，用投影出示“单价×数量＝总价”中的正比例和反比例关系。接着出示“速度×时间＝路程”，让学生同样说出这个数量关系中的两个量成正比例和反比例关系。然后依次出示“工作效率×工作时间＝工作总量”，以及“圆柱底面积×高＝圆柱的体积”，并分别让学生说出每一数量关系中两个相关联的量成正比例和反比例关系。最后提出：从“已完成的工作量＋未完成的工作量＝工作总量”这个数量关系中能找到正比例和反比例关系吗？引导学生在交流中进一步明确具有和、差关系的两个量不能成正比例，也不能成反比例。根据学生的回答，投影逐步呈现成如图1的情况（过程略）。

评析：以上环节除了让学生回忆正比例和反比例的概念，还通过逐一出示常用的数量关系，引发学生回忆与乘法有关的数量关系，当其中一个量一定时，另外两个量就成正比例或反比例关系。在投影上我们特意把数量关系都以乘法形式呈现，要求学生看到“乘”自觉地联想到“除”，从而减少对数量关系的记忆。

二、呈现完整题组，引发判断列式

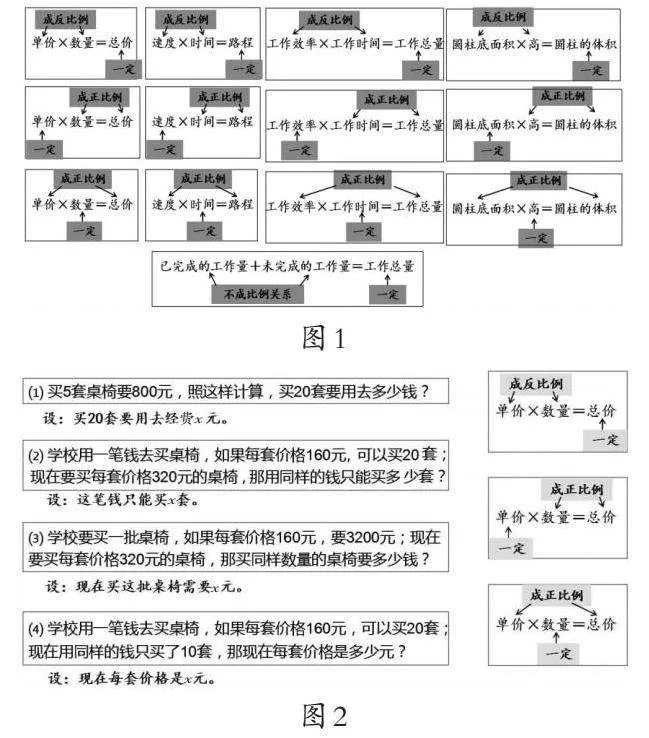
投影出示图2，提出要求：

先判断每一道题中两个相关联的量成什么比例，并与相关数量关系连上线后再列出方程（不计算）。学生独立完成后，组织集体交流。

生：第（1）题中单价不变，总价与数量成正比例关系，要同第二个数量关系连线。列出方程是：[8005]=[x20]。

师：如果把以上比例式写成“[205]＝[x800]”，你觉得可以吗？

生：可以的，利用比例的基本性质，这两个比例式都可以写成“5x＝800×20”，说明第二个式子是成立的。

师：你们能结合实际问题具体地说一说“[205]”与“[x800]”表示什么关系吗？

生：“[205]”表示现在买的20套是原来买的5套的几倍，“[x800]”表示现在买x套所需的钱数是原来买800套所需钱数的几倍。因为买桌椅所需的钱数与买的套数成正比例关系，所以这两个倍数应该是相等的。

师：是的，成正比例关系的两个量除了相对应的两个数的比的比值相等，也可以写出两个同类量中相对应的两个数的比的比值（倍数）相等。谁再来说说第（2）题属于什么问题？列出的方程又是怎样的？

生：第（2）题中总钱数一定，单价与数量成反比例。列出的方程是：320x＝160×20。

师：如果这里相关联的两个数量按同类量写成比例形式，该怎么写呢？

生：可以写成“[320160]＝[20x]”。

师：针对这个比例式，你能具体地说一说两个比表示实际数量的什么关系吗？

生：“[320160]”表示现在每套的单价是原来单价的2倍，那“[20x]”表示原来可以买的20套是现在可以买的x套的2倍。它们对应的两个数的比，刚好是另一对应的两个数的反比。

师：说得好！大家听懂他说的意思了吗？

学生表示听懂了。

师：是的，成反比例的两个量除了能找到相对应的两个数的积相等，也可以写成同类量中相对应的两个数的比，等于另外一组同类量相对应的两个数的反比。

接着教师继续引导学生交流。

第（3）题属于正比例问题，方程是“[3200160]＝[x320]”或“[3200x]=[160320]”。

第（4）题属于反比例问题，方程是“160×20＝10x”或“[1020]＝[160x]”。

让学生分别说出判断的理由，以及根据什么数量关系列出方程（过程略）。

评析：我们根据“单价×数量＝总价”这一数量关系，并围绕着学校购买桌椅的同一情境编成正比例和反比例题组。学生先判断、连线、列式，接着教师在组织交流时，除了让学生说出自己的一种列式方法，还特意提出从另一角度寻找对应数量的比以及列出的方程，并继续组织交流，使学生在分析交流中进一步梳理出解决正比例和反比例问题的方法。

三、呈现部分信息，引发判断补充

1.投影呈现图3，提出要求：

根据每道题的已知条件和所列出的方程，想一想题中两个相关联的量成什么比例，再把条件和问题补充完整，并写出所设的未知数。

学生独立思考后，组织集体交流。

生：从第（1）题的已知条件“5天组装了280辆；照这样计算”，可以知道每天组装辆数不变。再从所列的方程中也可以看到工作效率不变，工作总量和工作时间发生变化。方程中的“x”对应的是25天的工作量，所以在题目上要补充的条件和问题是“25天可以组装多少辆”。

师：那这一题的判断要填上什么？又怎样设未知数？

生：要填上“组装的辆数”与“天数”成正比例关系。要设：25天可以组装x辆。

教师根据学生的回答，继续把第（1）题的空格填完整后又提出：那第（2）题怎样判断？怎样填呢？

生：从第（2）题的已知条件和所列出的方程，可以知道工作总量不变，工作效率和工作时间成反比例。

教师在投影上先填上判断“每天组装辆数”与“天数”成反比例。接着提出：题目中还要填上怎样的条件和问题？

生：应该填上“如果每天多组装14辆，那要多少天可以完成”。

师：你是从哪里看出每天要多组装14辆的？

生：我从“（56＋14）x”表示这一批要组装的总辆数中看出来的。原来每天组装56辆，现在每天要组装“56＋14”辆。

师：好！刚才我们围绕这个小车组装问题，分析了工作效率、工作时间和工作总量关系中的正比例和反比例问题。下面我们找一个有关图形的问题，你还能分析、判断和填空吗？

2.投影出示图4，提出要求：

根据每题已知的条件和所列出的方程，想一想题中两个相关联的量成什么比例（填在括号里），再把条件和问题补充完整，并写出所设的未知数。

学生独立思考后，教师组织集体交流：

生：第（1）题中先要填上“高”不变，再填上“如果体积是480立方厘米，那么底面积是多少平方厘米”。

生：在下面的括号里要填上“体积”与“底面积”成“正”比例。

生：第（2）题中先要填上“体积”不变，接着填上“如果底面积是24平方厘米，那么它的高是多少厘米”。下面的括号里要填上“底面积”和“高”成“反”比例。

教师根据学生的回答相机在投影上填出后提出：这几位同学的填法你们同意吗？学生观察投影后表示赞同，接着教师又提出：还有别的填法吗？学生再次观察、交流后，有学生提出：我觉得第（2）题方程中的“24”不一定指圆柱体的底面积，还可能是圆柱体的高。如果把“24”看成圆柱的高，那未知数“x”就表示圆柱体的底面积。

师：大家听懂这位同学说的意思了吗？

学生表示听懂了。

接着教师指出：那题目中应填上怎样的条件和问题？

生：应该填上“如果体积”不变，“高是24厘米，它的底面积是多少平方厘米”。

师：真棒！我们在解题时要做到全面地思考问题，比如像第（2）题就有两种可能。我们就要把两种可能都补上。

评析：以上环节与上一环节的训练形式有很大的不同，它需要学生针对问题的部分条件，再结合给出的方程进行综合分析，才能对两个相关联的量的关系作出判断，并确定要补充的条件和问题。创设新的练习形式不仅能激发学生的练习兴趣，更重要的是通过这种形式的练习更好地培养了学生的分析能力。另外，我们在这一环节的练习设计中又涵盖两个数量关系，第1组是围绕工作效率、工作时间和工作总量展开的；第2组是围绕圆柱体的底面积、高和体积展开的。在第2组中，我们对第（2）小题的数据作了精心设计，使学生通过分析想到有两种可能的填法。借此练习促使学生养成全面综合分析问题的习惯。

四、结合图象解读，增强思辨训练

投影出示下面题组和要求1：

1.用比例的方法写出下面各题的方程（不计算）：

①一辆车从甲地到乙地，如果按80千米/时的速度，行完全程需要6小时；如果按120千米/时的速度，行完全程需要多少小时？

②一辆车在2小时内行了200千米，照这样的速度，6小时能行多少千米？

学生独立思考列出方程后，汇报如下：

第①题：设行完全程需要x小时。列出方程：80×6＝120x。

第②题：设6小时能行x千米。列出方程：[2002]=[x6]。

接着投影出示要求2和图5：

2.按以上每道题中两个相关联的量的变化规律画图，第①题要选图（ ），第②题要选图（ ）。并说明为什么。

学生独立思考后，组织集体交流：

生：第①题中两个相关联的量成反比例。要选图D。

师：为什么要选图D，而不选图C呢？

生：因为第①题中行驶的总路程是一定的，都是480千米，而图D中对应的“速度×时间”都刚好是480千米，所以第①题应该选图D。

教师和学生一起在图上找出几组速度与时间的对应点来验证，使全体学生清楚地看出按第①题中两个相关联的量画出的图确实是图D。接着教师又提出：那第②题又应该选哪幅图呢？

生：因为第②题中速度都是100千米/时，路程与时间成正比例，所以要选图A。

师：是吗？大家看看图A，路程200千米，对应的时间是2小时；当路程是400千米时，对应的时间是4小时；当路程是600千米时，对应的时间是6小时。路程除以对应的时间都刚好是100千米。这样第②题确实要选图A。

接着投影出示要求3：

3.请你根据图B和图C，把以上两道题的条件或问题进行改编，使改编后的题中两个相关联量的变化规律分别符合这两幅图。

学生独立思考后，组织集体交流（略）。

评析：以上这组练习围绕“速度×时间＝路程”这一数量关系展开，练习方式与上两个环节又有了很大的不同，更加凸显了结构化的训练。练习时先要求学生根据完整的问题进行判断、列式；再分别针对每道题作出图象的选择和说理；然后引导学生针对另外的两个图象，分别对原题作出多种方法的改编。由此可见，学生经历了这样的判断列式、图象选择、据图改编的练习后，对正比例和反比例问题中变与不变，以及两个相关联量的相依变化规律有了更深的理解，同时较好地提高了分析问题、解决问题的能力。

（作者单位：浙江临海市大洋小学，临海市教研中心）