最优化理论与方法课程教学创新性体系研究

舒万能　蹇文成　聂绍良　葛欣

［摘 要］最优化方法是现代管理科学的重要理论基础和不可缺少的方法，被人们广泛地应用到计算机科学、智能科学与技术、经济管理、国防等领域。最优化理论与方法课程是高校人工智能专业一门专业必修课程，为学生熟悉现代最优化理论及方法的设计和应用打下良好的基础。文章探讨了该课程实践教学的现状及其存在的问题，分析了该课程目标达成度与实践教学创新性体系的研究方法与实践措施。

［关键词］最优化理论与方法；实践教学体系；计算机科学与技术；人工智能; 精品课程

［中图分类号］ G642.0 ［文献标识码］ A ［文章编号］ 2095-3437（2023）17-0033-03

在人工智能时代，人工智能专业相关课程的实践教学是培养和提高学生编程能力和创新能力的重要环节。最优化理论与方法课程作为高校人工智能本科专业的一门专业必修课，以数据结构、算法设计与分析等课程为专业基础，课程的创新性体系研究对培养高素质、创新型、复合型人才有重要的促进作用[1-2]。虽然国内大部分高校人工智能相关的课程开设较早，但人工智能学科成立的时间比较晚，尤其是面向高考招生的人工智能专业，基本上是近五年才开始的。最优化理论与方法作为人工智能专业的核心课程，其实践教学与创新性体系尚处于起步建设阶段，加强实践教学是实现人才培养目标和提高人才培养质量的迫切要求[3-4]，是实施国内“双一流”高校建设的内在要求和重要内容。

最优化理论与方法课程主要分析最优化方法在计算机科学、智能科学与技术、经济管理、国防等领域的作用[5]，研究最优化基本要素和一维最优化方法搜索区间的确定，重点在于分析线性规划的求解原理和过程，以及整数规划数学模型和穷举法，同时设计非线性规划中的多目标优化模型。通过该课程的学习，学生能够掌握最优化方法的研究对象、特点，最优化方法模型的建立和模型的分析、求解、应用，线性规划问题的模型、求解及其应用，动态规划的模型、求解、应用等内容；掌握最新的智能优化方法和动态规划，为学生熟悉现代最优化理论及方法的设计和应用打下良好的基础，以适用人工智能相关事业发展对人才的新要求。

随着人工智能技术的日渐成熟，尤其是ChatGPT异军突起，社会各行各业对人工智能专业的关注度日渐高涨，人工智能方向的人才需求与日俱增，研究和探索新时期人工智能专业应用型人才培养模式，培养满足社会需求的人工智能人才，是我国不断突破高新技术、解决“卡脖子”技术的重要保障。因此，面向大学生的最优化理论与方法课程实践教学与创新性体系研究，是人工智能本科专业人才培养势在必行的课程改革任务。

一、最优化理论与方法课程教学的现状分析

目前，外国高校的最优化理论与方法课程主要对研究生开设，课程的实践教学方法主要采用理论联系实际的教学方法，旨在培养具有创新意识的高素质工程技术人员。国内高校的最优化理论与方法课程在大部分院校开设的学时数为32学时，课程的实践教学沿用传统的教学方法，多数实验是按照具体指导书进行的验证性实验，缺乏创新，在实验过程中很难融入学生自己的思想。

在课堂教学环节，学生要学习的内容较多，而且涉及的知识面比较广、比较深。分枝定界法和黄金分割法的计算原理虽然比较简单，但求解过程比较复杂。Hopfield神经网络、模拟退火算法和遗传算法这些人工智能算法构思巧妙，但运行机理复杂，运行的时间和空间复杂度较大[6-7]，对于本科生而言，学习难度系数较大，大多数学生对综合分析题目存在谈题色变的情况。在历届本科生的期末考试中，該课程的最终考试结果虽然比较理想，但分值分布极不均匀。所以，在新时代教学形势要求下，实现最优化理论与方法的过程考核机制与实践教学创新性体系并轨运行，是当前课程教学改革的重要举措。要以“课程体系化、教材精品化、师资团队化”的人工智能专业系列课程改革思路为指导，构建以实践能力、创新能力训练为特色的课程目标达成度与实践教学创新性体系。

二、最优化理论与方法课程目标达成度模型设计

最优化理论与方法课程经过不断改革、完善，探索出了一条提高学生实践能力和创新能力的新途径。该课程以掌握整体优化的知识结构为基础，把实践教学、创新能力培养贯穿于课程体系设计、落实以及人才培养的全过程，形成行之有效的实践教学体系。为了准确评价学生的学习效果，全面考核每个学习环节，设计出该课程的课程目标达成度模型。该模型包含课堂测试、平时作业、期中考试和期末考试四个环节，并从目标分值和学生平均得分两个维度进行评估。

定义1 假设[ai]表示课堂测试的学生平均得分，[bi]表示平时作业的学生平均得分，[ci]表示期中考试的学生平均得分，[di]表示期末考试的学生平均得分，[a*i]表示课堂测试的目标分值，[b*i]表示平时作业的目标分值，[c*i]表示期中考试的目标分值，[d*i]表示期末考试的目标分值，则课程分目标i的达成度可以描述为：

[αi=ai+bi+ci+dia*i+b*i+c*i+d*i]。

定义2 假设[α1]表示课堂测试环节的目标达成度，[α2]表示平时作业环节的目标达成度，[α3]表示期中考试环节的目标达成度，[α4]表示期末考试环节的目标达成度，[β1]表示课堂测试的权重因子，[β2]表示平时作业的权重因子，[β3]表示期中考试的权重因子，[β4]表示期末考试的权重因子，则课程目标达成度可以描述为：

[α=i=14αi×β1， β1+β2+β3+][β4=1]。

三、预期效果与分析

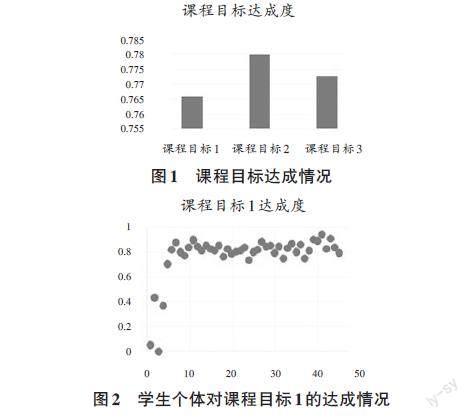
针对该课程教学存在的难点问题，课题组确立了讲授和实践相结合的授课方法，在教学过程中设计三个课程目标：一是掌握最优化基本要素，包括线性规划数学模型、线性规划求解基本原理，以及图搜索算法和人工神经网络模型；二是掌握常用的求解最优化问题的典型方法和基本原理；三是选用合适的最优化方法，设计系统的多目标数学优化模型，掌握人工智能方法的设计思路和求解过程。以湖北省武汉市某高校人工智能专业2020级某班45位学生为例，该班三个课程目标的达成情况见图1，学生个体对课程目标1的达成情况见图2，学生个体对课程目标2的达成情况见图3，学生个体对课程目标3的达成情况见图4。[0.785

通过图1的实验结果可以看出，通过作业、测验等进行考核，学生的课程目标达成度为0.766，说明大多数学生能够达成课程目标，效果较好，学生能够掌握相关知识并能应用其解决问题。在图2中，设定目标1里课堂测试的目标分值为30分，平时作业的目标分值为20分，期中考试的目标分值为20分，期末考试的目标分值为35分，最终有4位学生的目标1达成度低于0.6。图3和图4的实验结果显示，大部分学生的课程目标达成度超过0.6，极少学生计算题得分较低，部分学生的分析题没有作答导致目标达成度较低。针对上述存在的问题，可以采取以下措施：

第一，以实际最优化问题为导向，结合身边实际的最优化问题，引导学生思考，充分调动学生学习的积极性、主动性；引导学生深入讨论，各抒己见，从而达到发现问题、分析问题、解决问题的目的。

第二，强化学生的自主学习意识。课堂的内容只能作为一种引导，教师应当让学生掌握自主学习的方法，使学生能够利用各种资源，特别是网络资源的优势自行学习。利用实验室资源，面向全校学生开展研究性、创新型研究立项，鼓励学生申报研究课题，为学生提高研究能力创造条件。

第三，开展全方位开放式教学。改革传统的实践教学方法和手段，建立以工程能力培养为主线的实践教学体系与创新能力培养体系。加强与企业合作，校企联合培训教师、培养实践型和创新型人才，提高学生的竞争力。

第四，构建以实践能力、创新能力训练为特色的人工智能专业实践教学体系，改革实践教学内容、方式和手段，提高教学效果。

四、结语

随着社会的飞速发展，以科技创新为灵魂的人工智能时代已经来临。云计算、大数据、物联网、人工智能等将作为数字经济的重要技术支撑，为我国高端人才的培养和经济转型升级起到举足轻重的作用。最优化方法已成为现代管理科学的重要理论基础和不可缺少的方法，被人们广泛地应用到计算机科学、智能科学与技术、经济管理、国防等领域，发挥着越来越重要的作用。对于高校而言，产学研相结合促进了课程设置的改革，过程考核与目标达成度并轨，促进了教学方法的变革，能够提高学生独立思考和综合分析问题的能力，同时逐步培养大学生的科研意识。本文提出的最优化理论与方法课程目标达成度与实践教学创新性体系的构建，经教学实践的检验，具有较好的应用效果。在今后的实践教学过程中，课程组将进一步对教学内容、教学工具和教学方式进行研究和探讨，使其为最优化理论与方法课程的教学构建更有力的支撑平台。

［ 参 考 文 献 ］

[1] 黄平，孟永钢.最优化理论与方法[M].北京：清华大学出版社，2009.

[2] 傅英定，成孝予，唐应辉.最优化理论与方法[M].北京：国防工业出版社，2008.

[3] 袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，1997.

[4] 施光燕，钱伟懿，庞丽萍.最优化方法[M].北京：高等教育出版社，2007.

[5] 孙文瑜，徐成賢，朱德通.最优化方法[M].2版.北京：高等教育出版社，2010.

[6] SHU W N，CAI K，XIONG N N.Research on strong agile response task scheduling optimization enhancement with optimal resource usage in green cloud computing[J].Future generation computer systems，2021（124）：12-20.

[7] SHU W N，CAI K，XIONG N N.A short?term traffic flow prediction model based on an improved gate recurrent unit neural network[J].IEEE transactions on intelligent transportation systems，2022，23（9）：16654-16665.

［责任编辑：黄紧德］