刘老涧新闸有限元计算及振动特性分析

黄 毅，杜 亮，黄 凯，季 杰，管月婷，臧 伟

（1.江苏省骆运水利工程管理处，江苏 宿迁 223800；2.江苏省水利建设工程有限公司，江苏 扬州 225000；3.天津市宁河区水务局，天津 宁河区 301500；4.河海大学水利水电学院，江苏 南京 210098）

闸门是水工建筑物的一种重要挡水措施，其安全可靠程度对水工建筑物的正常运行起到关键作用，然而实际运行过程中，闸门会受到来自水流的激振荷载作用发生振动，同时闸门振动涉及结构力学与固体力学之间的相互耦合作用［1-2］，因此明晰闸门自身的振动特性对保障闸门及水工建筑物的安全运行具有较深的学术意义及工程意义。

目前国内外的专家学者针对闸门振动进行研究，主要依靠原型观测法、模型试验方法及数值模拟方法。蒋涛等［3］以江苏省秦淮新河水利枢纽节制闸为研究对象，针对闸门的静力分布及振动问题进行分析，探究了闸门振动频率与振动之间的相应关系。陶小平等［4］对闸门结构在启闭过程中的水力结构特征进行试验研究，获得了闸门结构在特定条件下的振动加速度及振动位移，揭示了闸门在闭门过程中的动力稳定特性。彭思贤等［5］采用数值模拟研究了大宽高比弧形闸门在水流脉动作用下的动力特性问题，基于随机振动法得到了闸门在脉动水流作用下的流激振动位移与应力响应。

本文以刘老涧新闸为研究对象，采用有限元静力计算，并对闸门的振动特性进行分析，以探究闸门的应力应变及振动的响应关系，旨在为同类型的闸门振动问题提供参考。

1 流场计算模型

1.1 三维模型及网格划分

采用三维建模软件对闸门上游连接段、闸室段及下游连接段按1∶1 比例建立三维模型，如图1 所示。在ANSYS ICEM 中对计算区域进行网格划分，流体部分节点数为659190，单元数为674422，最低的网格正交质量为0.263。水闸流体域网格如图2 所示。

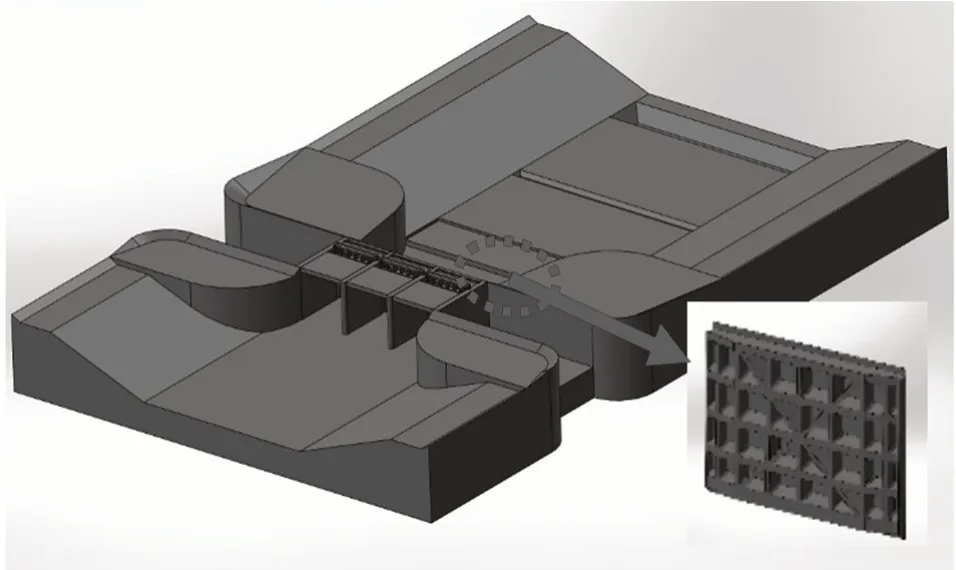
图1 上游连接段、闸室段及下游连接段三维模型

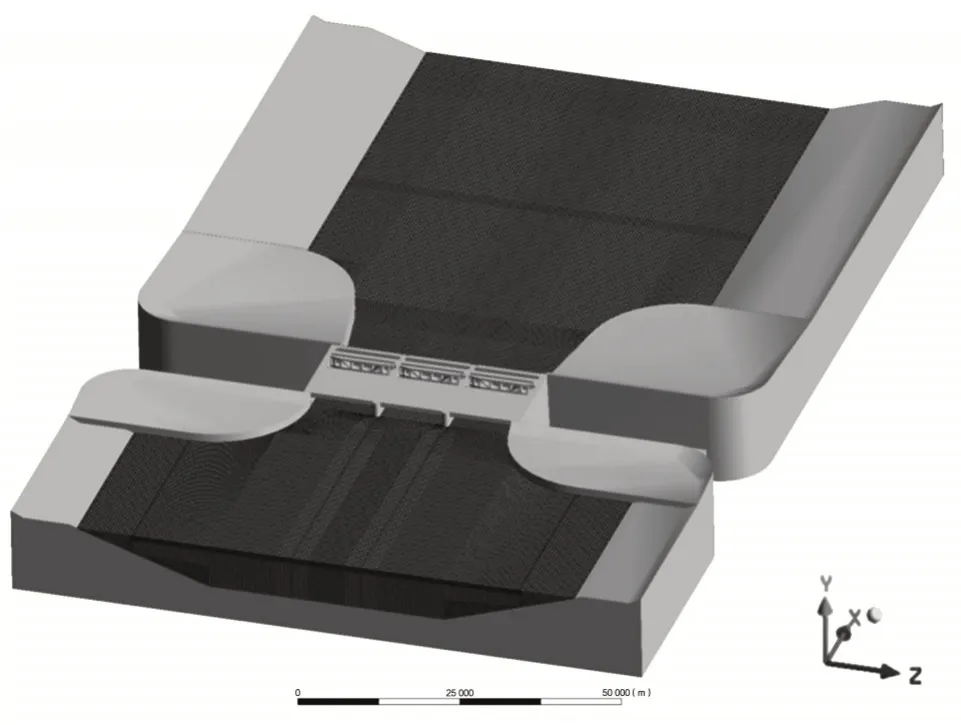
图2 水闸流体域网格

根据闸门结构形式和受力特点，将闸门面板、主横梁、纵梁、边梁、顶梁、离散为shell 181 板单元，底梁为bean189梁单元，闸门的固体域网格如图3所示，网格的节点总数为26353，单元总数为27042。

图3 闸门固体域网格

1.2 边界条件

采用ANSYS Fluent 对闸门上游连接段、闸室段及下游连接段的流体域进行三维流场数值模拟，选用RNGk-ε湍流模型封闭流动控制方程。考虑到流体域内流动的实际情况，流体域上方自由液面设置为对称边界条件；进水断面设置为进口边界条件；出水断面设置为静压自由出流边界条件；其余面都设置为壁面条件，收敛残差设置为10-4。

钢闸门材料Q235-B 钢，其材料参数为：弹性模量E=206 GPa，泊松比μ=0.25，密度ρ=7850 kg/m3。闸门固体边界条件分为载荷和约束，其中载荷有自身重力带来的重力加速度引起的惯性荷载和流体的压力作用于闸门结构的流固耦合面上产生的结构荷载；约束包括下支承座（只约束径向和切向，允许轴向上的移动）与联轴器端面（约束该面上的所有移动）。

2 闸门应力分析

2.1 面板应力

面板的折算应力如图4 所示，闸门面板共划分为9 个区域，如图4 所示，面板受到的最大折算应力为112 MPa，小于相应的容许值（1.1α［σ］=1.1×1.5×160=264 MPa），最大折算应力位于底梁、两侧边梁及纵梁组成的区格。

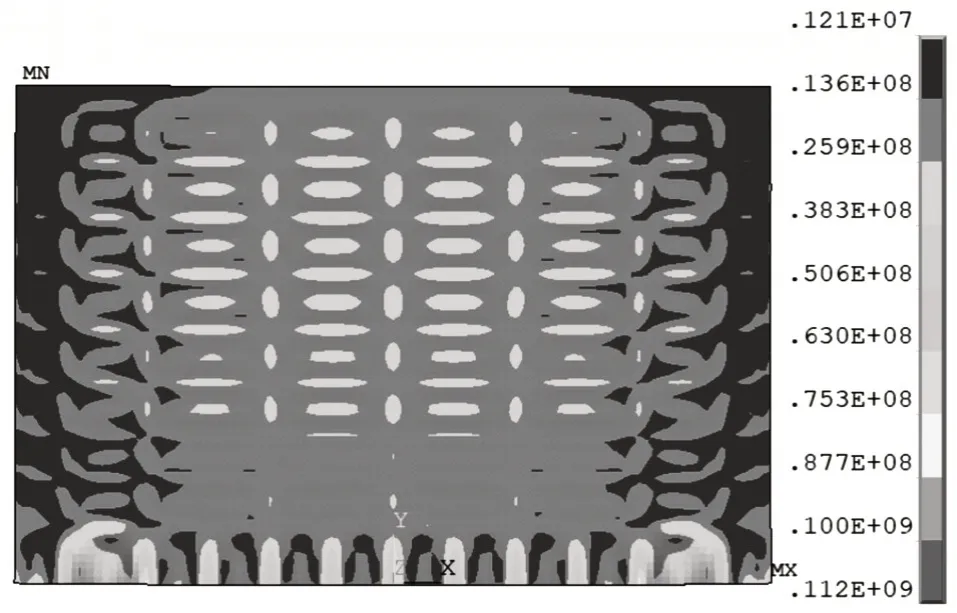
图4 面板折算应力

2.2 主横梁应力

主横梁正应力σx、切应力τ和折算应力σzh如表1所示，表中σx为主横梁沿轴线方向（x方向）的正应力，τ为主横梁腹板切应力，σzh为主横梁折算应力。由表1可知，各主横梁的最大正应力均小于相应的容许应力。各主横梁正应力最大值分布于主梁跨中后翼缘，1#、2#、3#、4#、5#主横梁最大正应力分别为：25.5 MPa、26.4 MPa、24.9 MPa、29.1 MPa、33.3 MPa；各主横梁的最大切应力均小于相应的容许应力，各主横梁最大切应力分布于主梁两端与边梁相交的腹板，1#、2#、3#、4#、5#主横梁最大切应力分别为：5.96 MPa、5.87 MPa、5.98 MPa、6.25 MPa、8.39 MPa；各主横梁的最大折算应力均小于相应的容许应力；各主梁的最大折算应力主要分布于主梁跨中的后翼缘，1#、2#、3#、4#、5#主横梁最大折算应力分别为：25.6 MPa、27.0 MPa、25.9 MPa、29.7 MPa、34.8 MPa。

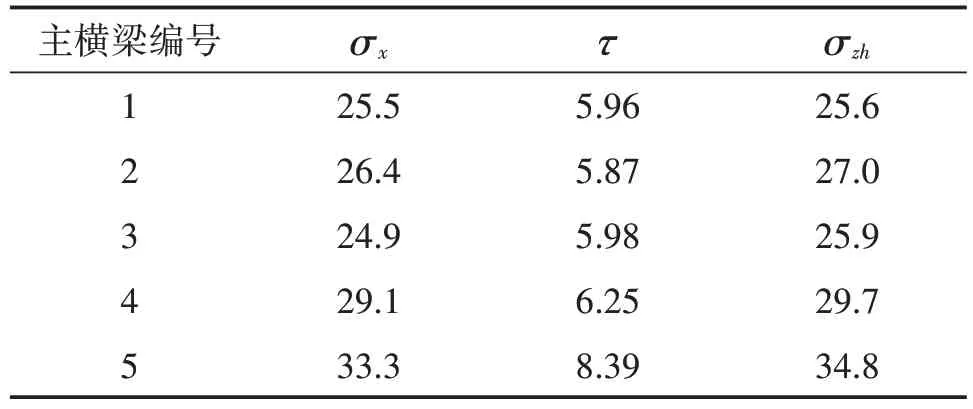
表1 主横梁最大应力 单位：MPa

2.3 边梁应力

边梁为T 字形截面组合截面梁，其应力分布如图5 所示，由图5 可知，组合截面边梁的最大正应力为6.31 MPa，位于边梁与2#次梁相交的翼缘，小于相应的容许正应力；组合截面边梁的最大切应力为2.68 MPa，位于边梁与底梁相交的腹板，小于相应的容许切应力；组合截面边梁的实际最大折算应力为13.8 MPa，小于相应的容许折算应力。

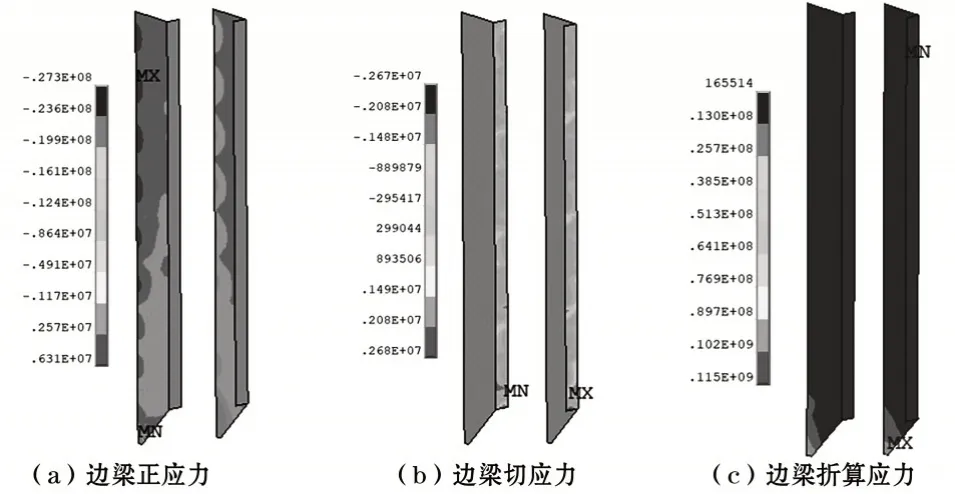
图5 边梁应力分布云图

2.4 纵梁应力

针对纵梁的应力分布进行分析，其应力计算结果如图6 所示，由图6 可知，纵梁的最大正应力为12.1 MPa，最大切应力为13.10 MPa，最大折算应力为21.5 MPa，均满足应力要求。最大正应力位于7#纵梁与底梁相交处；最大切应力位于3#纵梁与4#主梁相交的后翼缘；最大折算应力位于4#纵梁与3#主梁相交的后翼缘。

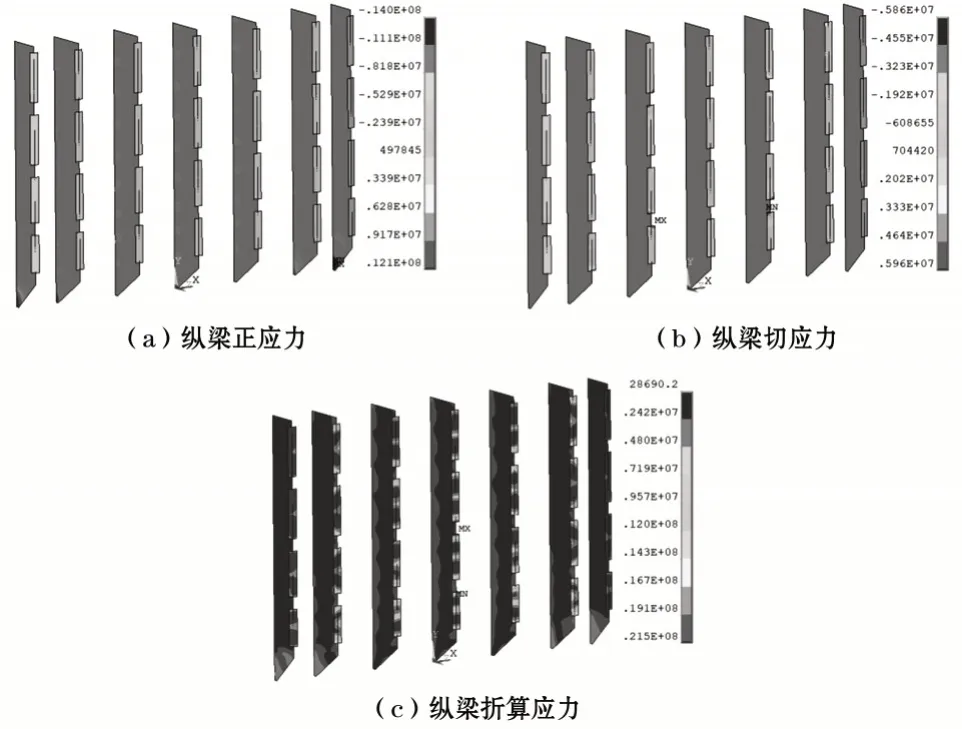
图6 纵梁应力分布云图

2.5 底梁应力

闸门底梁的正应力、切应力、折算应力如图7所示，由应力计算结果可知，底梁的最大正应力位于底梁与7#纵梁相交处，大小为1.88 MPa；底梁的最大切应力位于底梁与7#纵梁相交处，大小为3.8 MPa；底梁的最大折算应力位于底梁跨中处，大小为11.9 MPa。

2.6 次梁应力

次梁为钢板结构，共计4根，其正应力、切应力、折算应力如图8 所示，由次梁的应力计算结果可知，次梁的最大正应力位于4#次梁跨中处，大小为29.0 MPa；次梁的最大切应力位于4#次梁与边梁相交处，大小为5.12 MPa；次梁的最大折算应力位于4#次梁跨中处，大小为28.6 MPa。

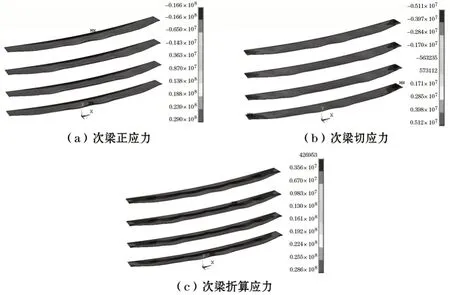
图8 次梁应力分布云图

2.7 主梁挠度

对闸门主横梁挠度进行计算，计算结果见表2，由表2可知，闸门1#～5#主横梁最大挠度为2.27 mm、0.65 mm，各主横梁最大挠度均位于主梁的跨中下翼缘，且各主横梁最大挠度均小于挠度容许值（13.5 mm）。

表2 主横梁挠度

3 振动特性分析

采用模态分析对闸门的振动问题进行分析，针对系统方程特征值和特征向量进行不同程度的求解，能得到闸门的固有频率及其相匹配的振型。闸门在运行过程中需考虑干模态和湿模态，其运动方程如下所示：

对于闸门的干模态，其结构系统内部的运动微分方程为

式中：[M]、[C]、[K]及[F]分别为闸门的质量矩阵、阻尼矩阵、刚度矩阵以及激励载荷向量；{ü}、{u̇ }及{u}分别为节点加速度列向量、速度列向量及节点位移列向量。

当阻尼为0 时，结构系统内部的运动微分方程可以表示为：

当水流经过闸门时，水流与闸门之间的耦合作用会影响闸门自身的振动特性，因此需考虑水流的激振对闸门振动方程的影响，即需要在闸门的质量方程中添加附加质量来模拟闸门。

对闸门的干模态和湿模态进行分析，得到了闸门在无水工况和7.5 m 水头工况下的前五阶振型，将设计水头下闸门在无水和考虑了流固耦合效应下的自振频率计算结果进行汇总，其具体数值如表3 所示。由表3 可知，7.5 m 水头工况下闸门的第2、3、4、5 阶自振频率均有不同程度的下降，因此，为准确分析闸门的自振特性，水流与闸门之间的流固耦合作用不容忽视。

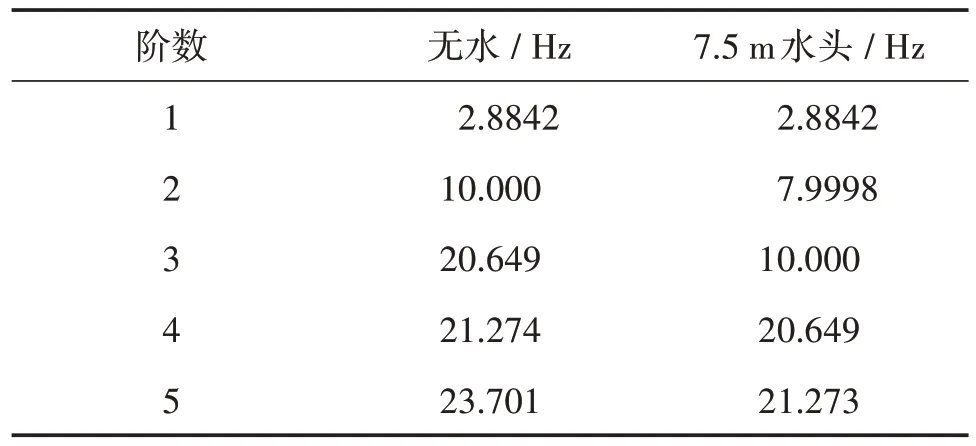
表3 不同工况下的闸门自振频率

4 结语

本文以刘老涧新闸为研究对象，通过对闸门进行有限元静力计算，分析了闸门的面板、主横梁、边梁、纵梁、底梁及次梁的应力分布，基于模态分析探究了闸门的自振特性，主要结论如下：

（1）边梁、纵梁、底梁及次梁的最大正应力、切应力及折算应力均满足应力要求。闸门最大正应力为33.3 MPa，位于主横梁跨中后翼缘，主横梁的最大切应力位于主梁两端与边梁交接的腹板处。

（2）7.5 m 水头下闸门的第2、3、4、5 阶自振频率相较于闸门在无水工况下的自振频率均有所不同程度的下降，因此，水体与闸门之间的流固耦合作用对闸门资者特性的影响不容忽视。