基于船舶操纵模拟器的大型滚装船泊稳条件试验方法

陈立家, 王冰, 魏天明, 许毅

(1.武汉理工大学航运学院,湖北 武汉 430063;2.武汉理工大学内河航运技术湖北省重点实验室,湖北 武汉 430063;3.武汉理工大学计算机与人工智能学院,湖北 武汉 430063)

0 引 言

系泊船舶的稳定是保证船舶安全系泊作业、提高装卸效率的基本前提。随着工业生产的迅速发展,能源和化工等行业大型工程不断地新建与扩建,其对大型化设备与物资的需求也越来越大。大件设备和大件模块往往需要通过水路运输,因此大型滚装船应运而生。由于码头前沿水域高程条件和水深条件的限制,以及大型滚装船自身质量大、重心高、惯性大,受风、流的影响大,运动状态难以控制等特点,大型滚装船停靠通常采用丁靠系泊方式。丁靠系泊,即船舶与滚装码头的前沿线垂直,呈“丁”字形,并由若干系泊缆绳将其与岸上系船墩连接在一起。该系泊方式可借鉴的经验较少,对环境要求较严格。因此,需要对大型滚装船的系泊安全进行分析,确定安全作业的极限环境条件。

从研究方法上来看,国内外学者对船舶系泊问题和环境载荷的分析主要采用理论计算、船舶物理模型试验、实船试验和OPTIMOOR软件分析等方法。刘明维等[1]建立了船闸浮式系船柱受荷响应力学模型,反映船舶缆绳系缆力与浮式系船柱柱身应变的关系。QI等[2]对码头系泊的液化天然气(liquefied natural gas,LNG)船的水动力性能进行了系泊模型试验研究,在试验过程中考虑了风、浪、流等环境因素对码头系泊系统的影响,并分别测定了不同海况下系泊系统的六个自由度运动响应和缆绳张力。董胜等[3]通过物理模型试验对青岛万达游艇码头项目进行了研究,测定了拟建码头附近水域的船舶泊稳条件。NGUYEN等[4]采用物理模型试验的方法,研究靠近港口的过往船舶所产生的波浪对系泊船舶运动和系泊缆绳张力的影响,测定了系泊船舶在不同海况下不规则波浪中的运动量和受力。周斌等[5]以中小型LNG船为目标船型,利用OPTIMOOR软件计算船舶运动和系泊缆绳受力。LEE等[6]使用OPTIMOOR软件,对船舶的敏感性进行分析,识别船对船过驳系泊中的影响因素,并基于试验结果建立了船对船系泊的安全标准。

虽然对船舶系泊分析的研究已有较多研究成果,但对大型滚装船丁靠系泊模拟的研究较少,且在研究过程中对环境因素有的进行了大量简化,有的采用定常设定的方式,未能反映出真实的动态环境场。为此,本研究提出一种基于船舶操纵模拟器的大型滚装船泊稳条件试验方法。采用理论推导与数值仿真相结合的方法,对系泊船舶的受力状态进行分析,以分离式船舶运动数学模型MMG(mathematical model group)为基础,构建系泊大型滚装船运动数学模型,并将其运用于船舶操纵模拟器中,基于实时模拟的动态环境场计算系泊船体运动量、系泊缆力和护舷反作用力;采用时域耦合方法,分析在不同环境载荷作用下的泊稳状况。以湛江港某4万t滚装船系泊为例,验证模型的正确性以及该模型用于开展船舶泊稳条件试验的可行性,并最终确定该船安全系泊的极限环境条件。

1 船舶系泊运动建模

为更好地描述大型滚装船系泊运动,以船体本身为参照,建立以船舶重心为坐标原点的附体坐标系,如图1所示:xoy与水平面重合;x轴与船舶首尾线重合,正方向指向船首;y轴与正横方向平行,正方向指向右舷;z轴垂直于xoy平面,正方向向上。

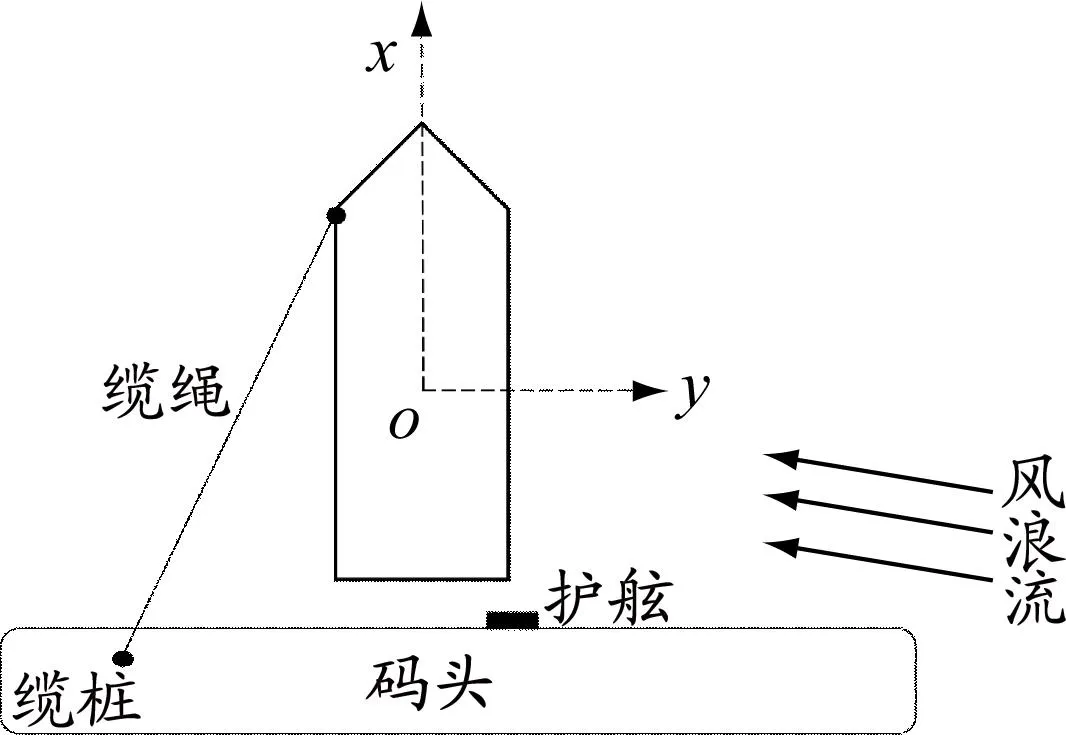
(a)俯视图

1.1 风载荷计算

大型滚装船在以丁靠方式系泊时,船舶处于无速、无舵效状态,且其受风面积比同吨位的一般货船的大,故风力对船舶运动的影响尤为显著。风速通常由平均风速vm和时变风速vt组成,其表达式为

vwind=vm+vt

(1)

时变风载荷的动力效应通过风谱体现。基于Davenport风谱,利用谐波叠加的方法,通过确定风速的时域历程来模拟时变风,然后加入平均风来模拟随机风。作用在船舶上的风载荷可以用Hughes公式进行计算,以纵荡方向的风载荷为例:

(2)

式中:ρ为空气密度;Cx,wind,α为纵荡方向的风力系数,下标α为风舷角;Af为水线上船体正面投影面积。

当船舶处于系泊运动状态时,风载荷力矩(以艏摇力矩为例)可表示为

(3)

式中:Cwind,α为艏摇方向的风力系数;As为水线上船体侧面投影面积;L为船舶总长。

1.2 水流载荷计算

水流的流速随时间的变化是相对缓慢的,在对大型滚装船水下部分所承受的水流载荷进行计算时,考虑恒定、均匀水流的干扰,纵荡方向的水流载荷的计算如下:

(4)

式中:ρsea为海水密度;Cx,current为纵荡方向的水流压力系数;vcurrent为水流流速;d为船舶吃水。

水流作用在船体水下部分几何中心处的艏摇力矩:

(5)

式中:g为重力加速度;Ccurrent为艏摇力矩系数;Lw为船舶水线长。

1.3 波浪载荷计算

在对系泊船舶进行波浪载荷计算时,考虑船体受到的波浪力随时间的正弦变化,而波浪力大小与船舶与波浪间的相对位置有关,因此将波浪力计算式写为

(6)

式中:Fm,wave为波浪力幅值,其引起船舶各自由度运动的具体计算方法参照文献[7];ξ′为波浪力坐标系中船舶的位置;λ为波长。

1.4 系泊缆力计算

系泊缆力的计算目前多使用文献[8]的计算模型。该模型给出了船舶在风、流作用下的计算式,但未给出船舶受到的波浪载荷的计算式。因此,在上述风、流模型的基础上,将波浪载荷加入计算模型中,得到船舶系泊缆力FL的计算式:

(7)

系泊系统一般都有多根系泊缆绳。由于各缆绳的受力情况类似,故缆绳对船舶的总系泊缆力可以用各缆绳系泊缆力之和表示。将系泊缆力在船舶坐标系中进行矢量分解(如图2中缆绳拉力示意图所示,A点为船上导缆孔,B点为岸上系缆墩),得到系泊缆力各方向分力的计算模型,船舶纵荡方向上的系泊缆力计算式为

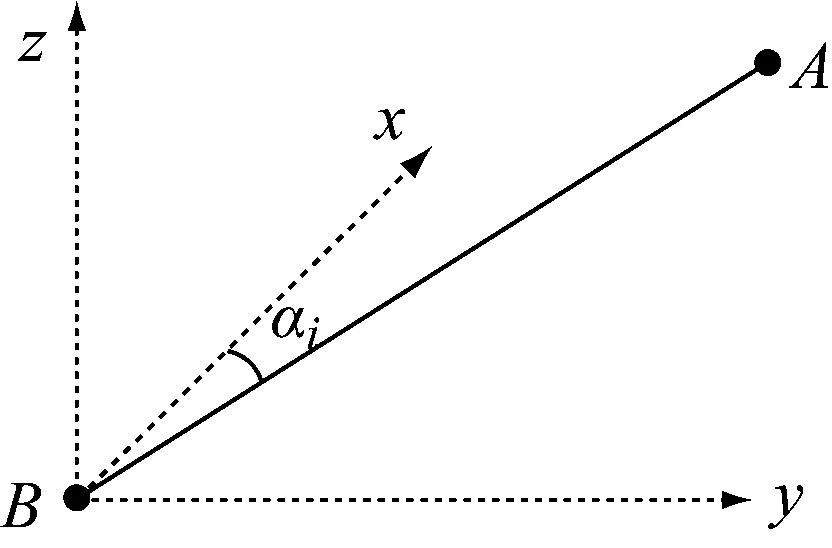
图2 缆绳拉力示意图

(8)

式中:n为缆绳数量;i为缆绳序号;αi为导缆孔与系缆墩连线的水平夹角;θ为船首向。

缆绳作用在船舶上的力矩(以艏摇力矩为例)可表示为

ML=

(9)

式中:xi、yi为缆绳i的导缆孔的x、y轴坐标值。

1.5 护舷反作用力计算

当船舶与护舷发生接触时,采用赫兹接触定律[9]计算接触力:

(10)

式中:Rs为船舶接触点处的曲率半径;Rb为护舷接触点处的曲率半径;νs为船体材料的泊松比;νb为护舷材料的泊松比;Es为船体材料的杨氏模量;Eb为护舷材料的杨氏模量;δ为接触时的形变量。

以纵荡方向为例,护舷对船舶产生的力可表示为

Fx,F=fsin(φ-φ)

(11)

以艏摇力矩为例,作用在船舶上的力矩可表示为

MF=fxccos(φ-φ)-fycsin(φ-φ)

(12)

式中:φ为船首与正北方向夹角;φ为码头方向;xc、yc为碰撞点的x、y轴坐标值,其可以采用点面碰撞来求解。

1.6 船舶系泊系统数学模型

基于MMG分离建模的思想[10],针对裸船体、螺旋桨、舵的结构构建船舶运动的基本数学模型。为实现系泊船舶运动数值预报,根据系泊作业要求,将系泊缆力、护舷反作用力和力矩施加到船舶六自由度运动模型中,得到系泊缆绳-船舶-护舷耦合模型:

式中:m为船舶质量;vx、vy、vz分别为船舶在x、y、z轴方向上的速度分量,即船舶的纵荡速度、横荡速度、垂荡速度;ωx、ωy、ωz分别为船舶绕x、y、z轴的角速度大小,即船舶的横摇角速度、纵摇角速度、艏摇角速度;Fx、Fy、Fy分别为船舶在x、y、z轴方向上所受合外力大小;下标H、P、R、L、F、wind、wave、current分别表示水、桨、舵、缆绳、护舷、风、浪和流;Ixx、Iyy、Izz分别为绕x、y、z轴的船舶惯性张量大小;Mx、My、Mz分别为船舶在x、y、z轴方向上所受合外力矩大小。

因为系泊作业时桨和舵往往处于停止状态,所以将模型中的桨力和舵力置零。船体水动力采用基本的横流模型来确定。

计算系泊系统运动的步骤如下:第一步,根据MMG模型计算船舶在自由状态时的运动模型,确定船位和导缆孔位置;第二步,将船位和速度传给护舷作用力模型,以便确定护舷反作用力,同时计算风、浪、流等环境载荷,并将其传给系泊缆力模型,根据模型计算缆绳系泊缆力;第三步,将计算得到的缆绳受力、护舷反作用力传递给系泊系统,用于求解船舶位置和速度等参数;第四步,重复第二步和第三步,直到船舶运动量不在许可范围内,结束计算。在各次循环中,须检验缆绳的张力是否超过其破断载荷。

2 仿真试验平台和流程设计

2.1 仿真试验平台

利用船舶操纵模拟器对大型滚装船的系泊作业进行数值模拟,其优势在于能够实现模型解算和人机交互。将构建的船舶系泊运动数学模型以动态库方式链接到船舶操纵模拟器仿真平台,通过输入船型参数和系泊参数等数据,即可计算在设定条件下的船体运动量、缆绳张力、护舷反作用力。这些信息在解算完成后被输入场景仿真模块中,驾驶控制台和视景显示系统显示出整体视景画面,操作员在三维虚拟环境中操作相关设备,体验接近实际的系泊操作。同时,信息输入到信息存储单元[11],通过提取实时的仿真数据,可以对船舶系泊安全进行全面分析。图3为使用船舶操纵模拟器进行系泊试验的场景。

图3 船舶操纵模拟器系泊试验场景

2.2 试验流程设计

基于船舶操纵模拟器的大型滚装船泊稳条件试验一般包括以下几个步骤,具体流程见图4。

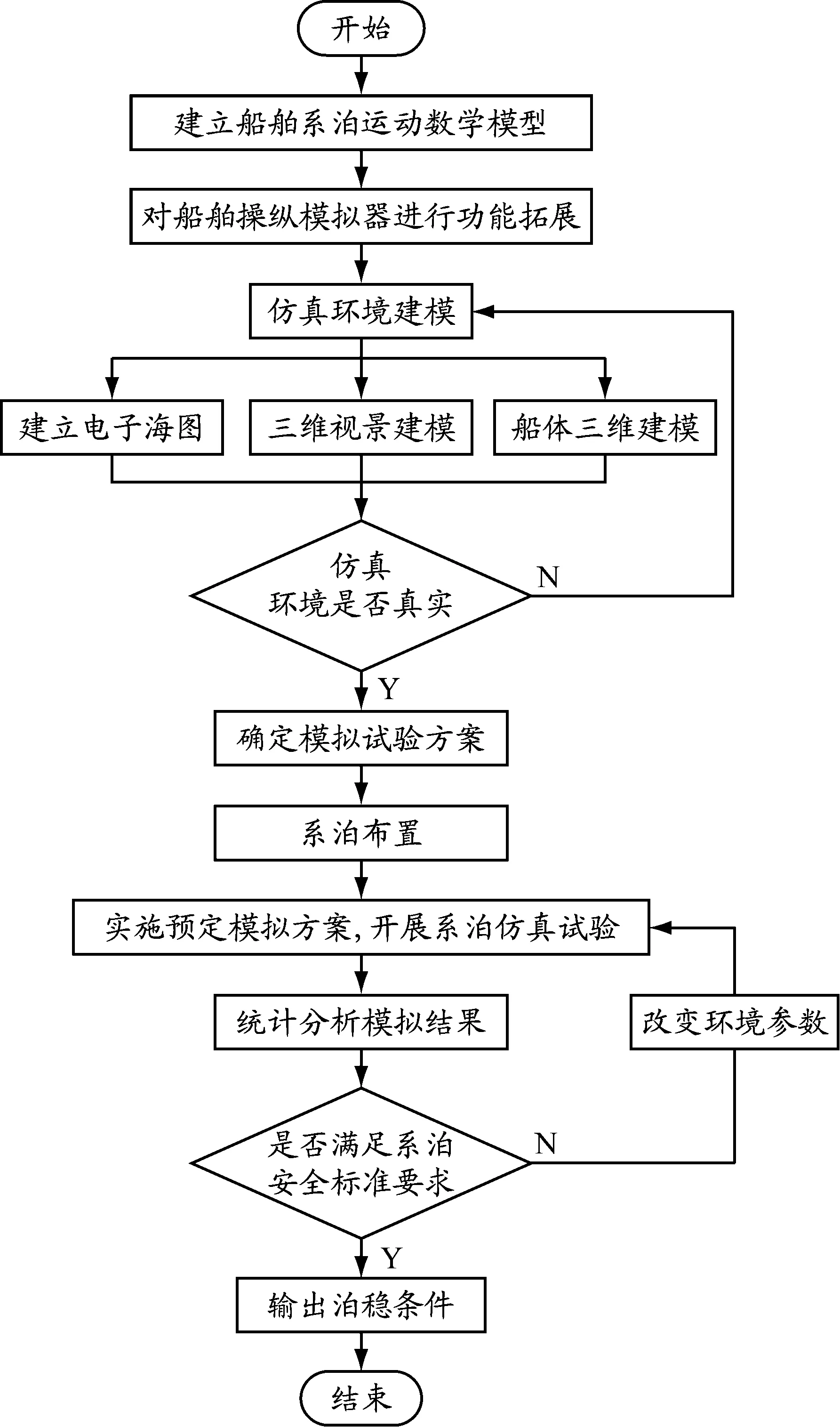
图4 大型滚装船泊稳试验流程

运用面向对象的Visual C#编程语言为大型滚装船系泊运动数学模型编程,并将程序导入船舶操纵模拟器中,对船舶操纵模拟器进行功能拓展,用于泊稳仿真试验:首先,对仿真环境进行建模,建立电子海图、三维视景模型、船舶模型,并逐一验证,确保在仿真环境下的模拟环境与实际水域环境一致,以及模拟船模与真实系泊船舶的尺度和操纵特性的相似性[12];其次,根据试验要求确定模拟试验方案,将船舶以丁靠方式置于码头前,根据确定的缆绳布置方案系带缆绳,并调整各缆绳初始系泊缆力;最后,采用人机交互试验的方法,运用船舶操纵模拟器进行实时船舶系泊操纵模拟试验。使用模拟器实时监控并记录风浪流环境、船舶运动信息和系泊缆力数据,选取相应的泊稳指标,结合相关规范,调整不同环境参数,直至获得大型滚装船的泊稳条件。

3 大型滚装船系泊仿真模型

3.1 试验船型参数

以湛江港某重大件滚装船码头项目为依托进行仿真试验,选用满载的4万t滚装船为研究对象。试验船型参数见表1,其尺度和操纵性能等与真实船的一致。

表1 试验船型主要参数

3.2 系泊系统布置

不同吨级的船舶使用的系泊缆绳数量不同,根据布置原则确定该4万t滚装船的系泊缆绳数量共8根。8根缆绳采用全倒缆的系缆方案,关于船舯呈对称分布,分别为2根艉缆、2根艉倒缆、2根艏缆和2根艏倒缆。系泊缆绳布置方式见图5。系泊缆绳均为截面尺寸为36 mm×20 mm的超高分子量的聚乙烯绳,8根绳的弹性、长度和质量相似;每根绳的最小破断力为790 kN,安全系数为2,即其允许的最大工作载荷取395 kN。码头上布置4组DA-A600H标准反力型橡胶护舷,每组最大压缩变形为55%,反力标准值为412 kN,4组护舷反力合计1 648 kN。

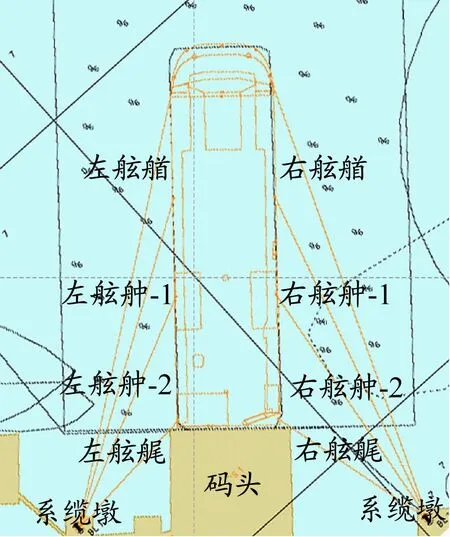
图5 系缆方案布置方式

3.3 动态环境参数

基于该滚装码头区域的水文、气象观测数据,假定在1 s内风的特征要素不发生变化,根据第1.1节的理论,循环计算出每秒的风场数据,完成3 h随机风的实时模拟。采用码头水域年测的平均波浪高度0.4 m和0.5 m,波浪和风的方向设置为同一个方向,实现对规则波的实时模拟。流场为均匀同向的定常流场,流向分别为310°(涨潮流)和130°(落潮流),流速均为0.3 m/s。

船舶停靠时所受到的风、浪、流的方向的定义见图6。定义环境载荷的入射方向与x轴正向的夹角为环境载荷的入射角,其中:当风、浪入射角为310°时,船舶为迎风、浪状态;当流向为130°时船首迎流,当流向为310°时船尾迎流。

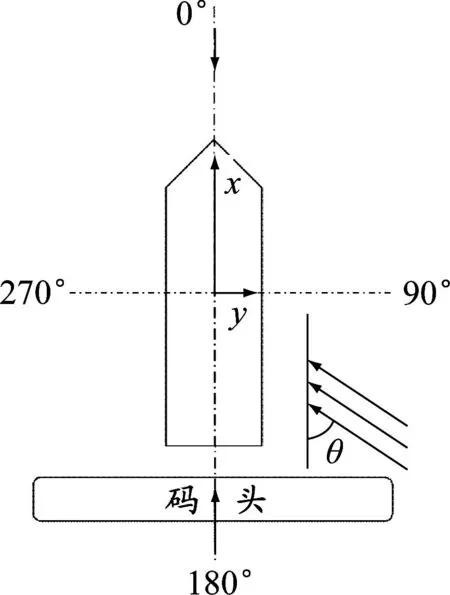
图6 环境载荷方向

为分析大型滚装船在风、浪、流共同影响下的泊稳特性,在考虑船舶左、右舷横向受力的基础上,根据风、流、波浪参数出现频率的大小,对泊稳的环境条件进行有效的预设,确定2组不同的环境参数,具体见表2。

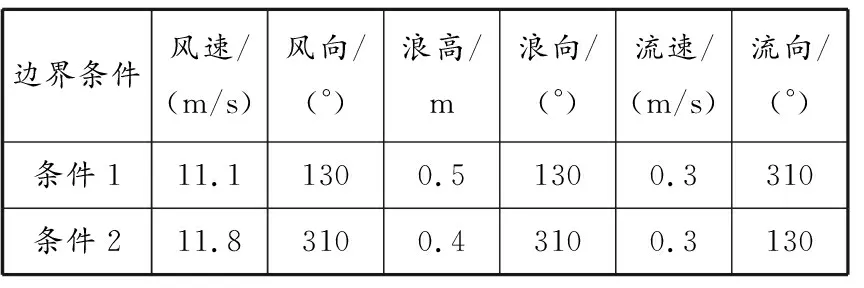
表2 边界条件预设

4 大型滚装船泊稳分析

4.1 泊稳衡准指标

目前国内外对船舶泊稳标准尚无统一规定。考虑到大型滚装船系泊的特点,选取船体运动量、系泊缆力、护舷反作用力这3个主要控制指标进行系泊安全评判。

系泊滚装船在风、浪、流等环境条件满足安全作业要求的情况下,通过船上跳板与码头相连,进行水平装卸作业。大型滚装船载货体积和载货质量比普通货船的大,在不同装载状态下船舶稳性变化大。为使船舶保持一定的平衡状态,确保跳板、活动车辆等特殊设备的正常使用,便于货物装卸,船舶不能产生大幅度的垂荡运动。文献[13-15]均对船舶运动量作出限制要求。对于滚装船采用船尾靠泊作业时的运动量,文献[15]给出了更严格的限制标准,规定了作业期间船舶六自由度运动量的允许值。若六个自由度的运动量未超出允许值,则认为系泊是安全稳定的,在运动量足够小的情况下船舶的稳性可以得到很好的保证。

系泊缆绳是线弹性的,在系泊作业过程中长期处于拉伸状态,伴随有逐渐明显的弹性变形效应,其张力急剧增大。当缆绳最大张力大于其破断载荷时,系泊作业的安全稳定性遭到破坏。因此,本研究在大型滚装船运动的基础上叠加系泊缆绳的弹性变形,考虑发生弹性变形时系泊缆绳的张力变化。国内规范对缆绳载荷的限制标准没有给出准确规定,参考文献[16]对船用系缆允许负荷的规定:钢丝绳不超过其破断强度的55%,尼龙绳以外的化纤绳不超过其破断强度的50%,尼龙绳不超过其破断强度的45%。高强度纤维绳可参照一般化纤绳,允许负荷取破断强度的50%。以缆绳受力是否超出安全负荷对缆绳进行破断分析。在码头前沿设置的护舷设备对船舶泊稳性有着至关重要的作用,其主要由护舷压缩量决定,多依据文献[13]和[17]计算。与载荷规范相比,文献[13]不仅考虑了船舶正常靠泊,而且考虑了船舶异常靠泊行为,考虑的因素更为精细、全面和合理。因此,参照文献[13]对护舷压缩量的规定,最大反作用力引起的形变不得超过52.5%的压缩形变量。当护舷反作用力超过其设计反力时,则认为护舷强度不满足要求。

4.2 船体运动量分析

通过求解系泊船舶六自由度运动模型,得到不同风、浪、流条件下系泊滚装船运动量的变化数据,对其最大值进行统计并与规范值进行比较(见表3)。

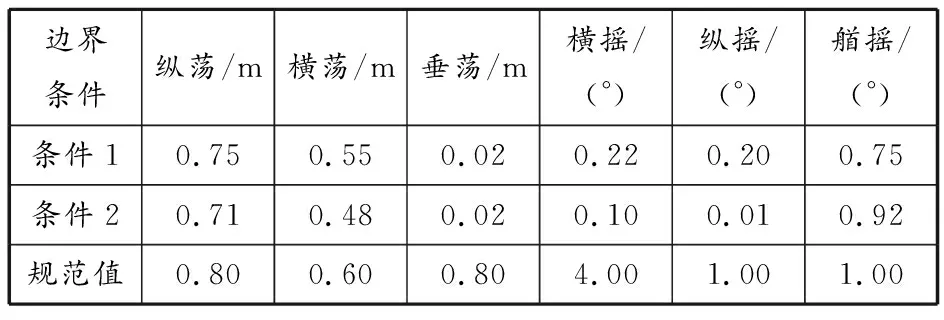
表3 船舶六自由度运动量最大值对比

图7和图8给出了在以上两组设定环境条件下,系泊船舶在6个自由度(纵荡、横荡、垂荡、横摇、纵摇、艏摇)上的运动变化曲线,其中“+”表示各自由度的正方向,“-”表示各自由度的反方向。

(a)沿x、y、z轴的往复平动

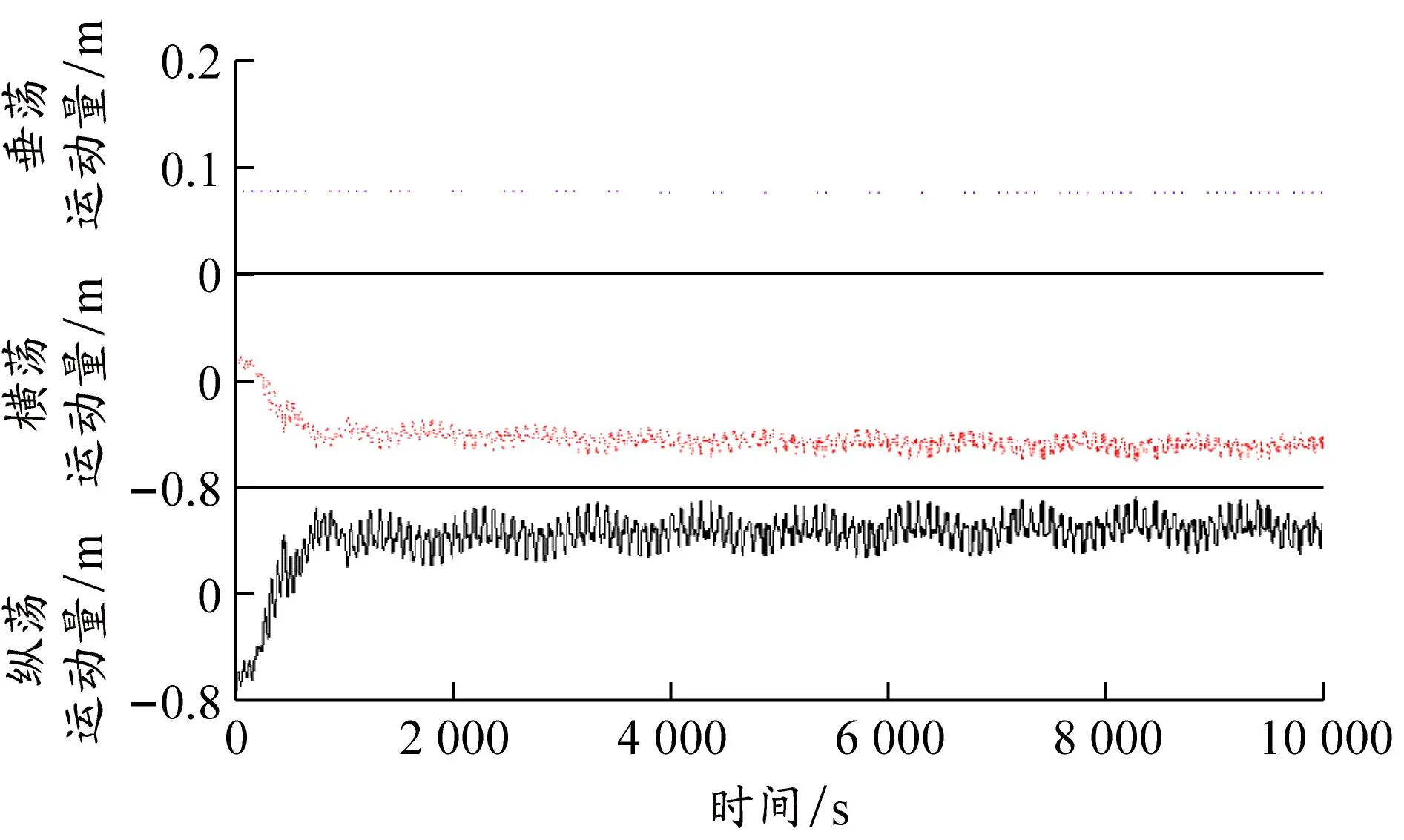
(a)沿x、y、z轴的往复平动

对比不同工况下船体运动量的时间历程曲线可知,在风、浪、流等的冲击下系泊船舶船体的运动极其不规则,由于缆绳的约束,船舶在6个自由度上的运动在不同环境下呈现出不同的特性。由于不同风速、风向、流速和浪高的随机作用,系泊船舶产生剧烈的纵荡运动,初始时先产生向后的位移,随后受缆绳的影响运动幅值逐渐减小,并进行随机的往复纵荡运动;横荡运动幅度在前1 000 s内逐渐减小并开始随风、浪、流随机变化。与纵荡和横荡运动幅值变化较大相比,垂荡时历曲线一直在零水平附近振荡。系泊船舶除产生平动外,还发生转动。在载荷突然作用时,艏摇角在前1 000 s内运动幅值逐渐减小,随后随风、浪、流随机变化。横摇和纵摇时历曲线长期稳定在零水平附近波动。

4.3 系泊缆力分析

通过求解系泊模型,可得到系泊缆力在不同风、浪、流环境条件下随时间的变化情况,分别绘制船舶各缆绳持续受力变化曲线,见图9～12。

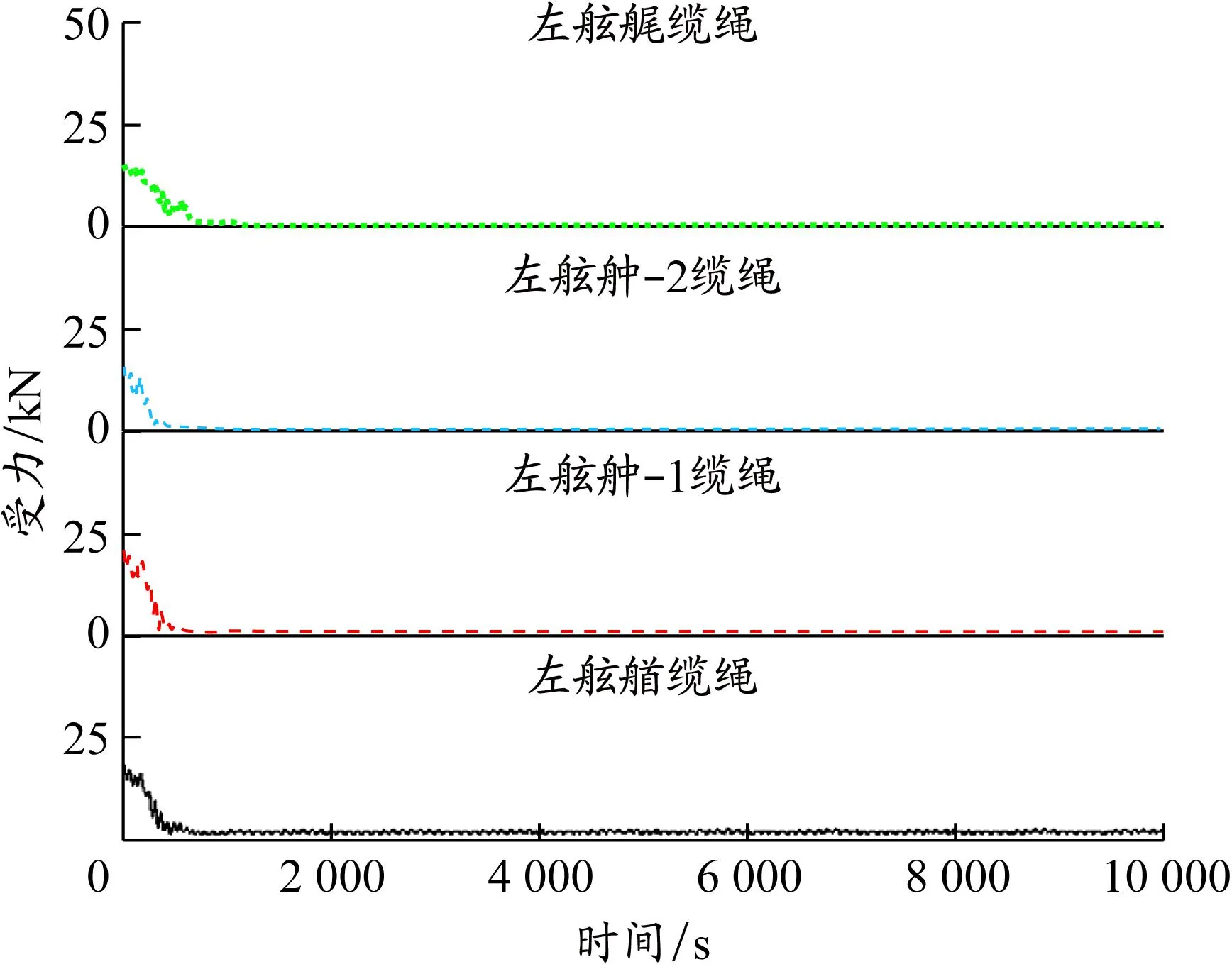
图9 左舷各缆绳受力变化(条件1)

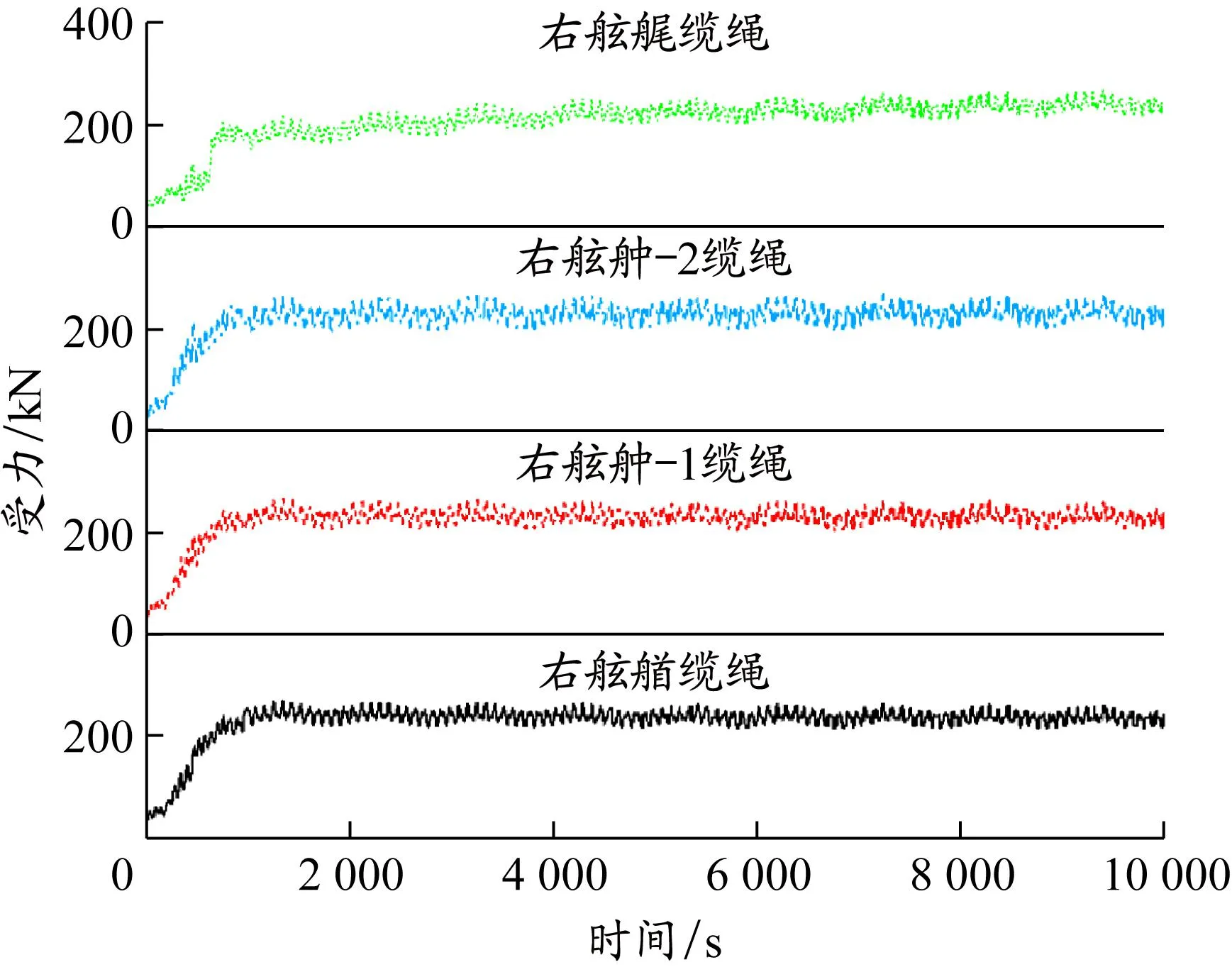
图10 右舷各缆绳受力变化(条件1)

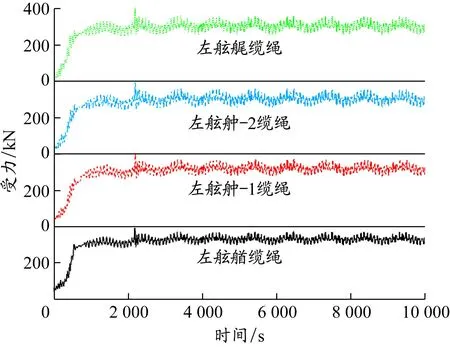
图11 左舷各缆绳受力变化(条件2)

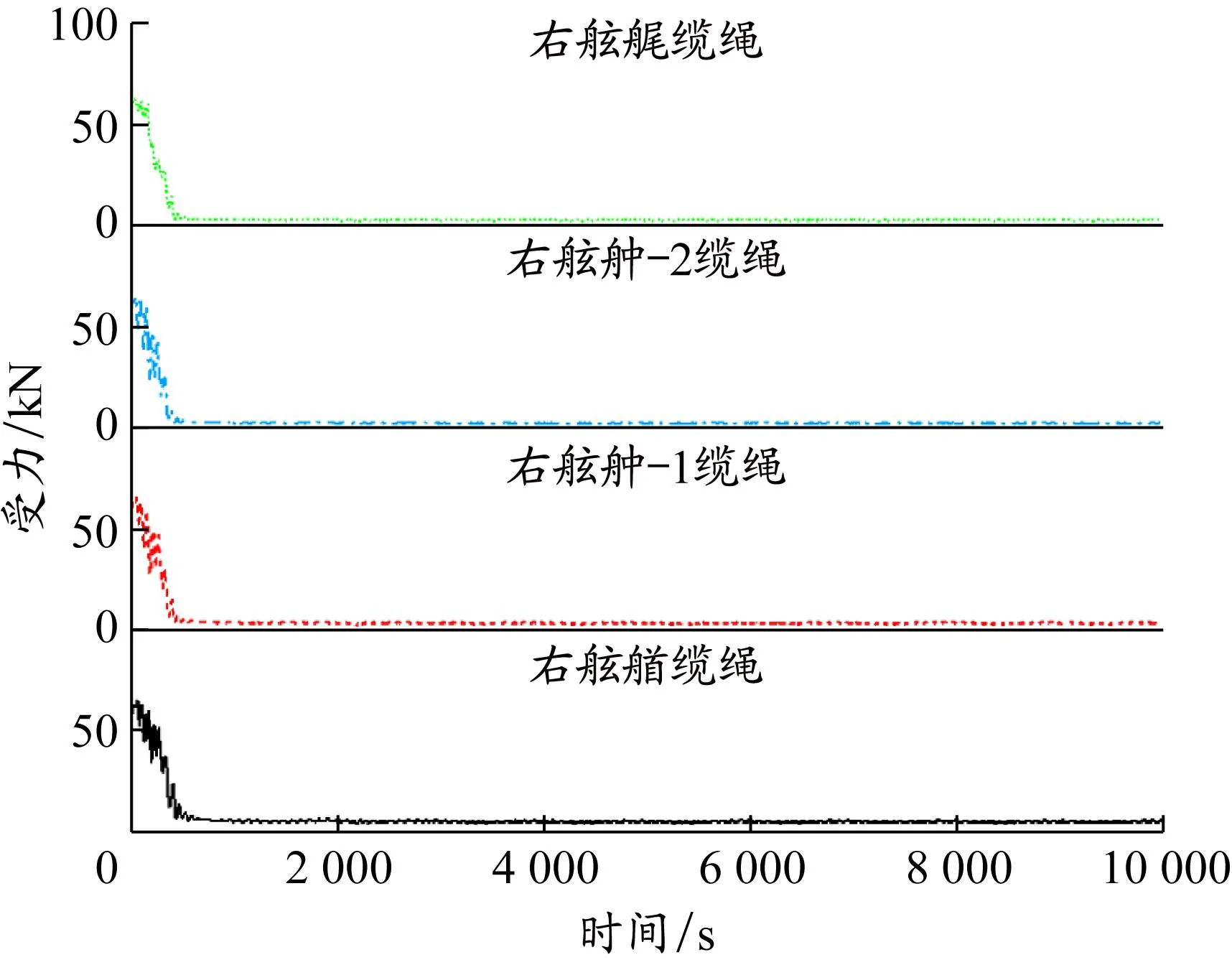
图12 右舷侧各缆绳受力变化(条件2)

由图9～12可以看出,环境载荷对系泊缆绳受力有着重要影响。外界环境的剧烈变化对系泊缆绳产生较大的扰动,所有系泊缆绳张力变化显著,且随后缆绳受力出现了很明显的振荡。这是因为缆绳拉动船体运动时,船体产生六自由度运动,缆绳出现张紧和松弛交替循环的动态过程,从而造成缆绳受力的不断振荡。各缆绳所受力大小各不相同,船舶左右两舷的缆绳受不对称作用力,迎流侧的比背流侧的大。同侧缆绳的受力非常接近,因为在系泊时船舶艏艉的运动比较相似,其时历曲线基本接近,系泊缆力的数值大小相近。

4.4 护舷反作用力分析

通过数值计算得出在风、浪、流环境载荷作用下码头护舷的反作用力值,并与反力标准值进行比较。

随着船舶与码头接触过程的进行,护舷被完全挤压,同时给予船舶反作用力使得船舶反弹离开码头。在系泊缆绳控制工况下,条件1和条件2下的护舷最大反作用力分别为1 324、1 079 kN,均小于护舷的设计反力标准值1 648 kN,此时该护舷完全满足4万t滚装船系泊的使用要求。与条件2相比,条件1的护舷反作用力更明显,这是因为随着风浪流的大小和方向发生改变,船舶与码头接触的着力点位置及接触力大小发生了变化,从而使得护舷反作用力的大小也发生改变。

4.5 计算结果与OPTIMOOR软件分析结果对比

为验证船舶系泊运动数学模型的精度,同时避免使用同种软件进行验证时出现的误差,采用OPTIMOOR软件进行计算对比,按照图7设计的系缆布置方案进行模拟计算后,得到不同环境下的系泊船体运动量(横荡、纵荡、垂荡和横摇4个运动量)、系泊缆力和护舷受力数据。由于论文篇幅限制,只取条件1下的试验结果进行验证,见表4～6。

表4 相似工况下船舶4个自由度上的运动量计算结果对比

表5 各缆绳受力对比 单位:kN

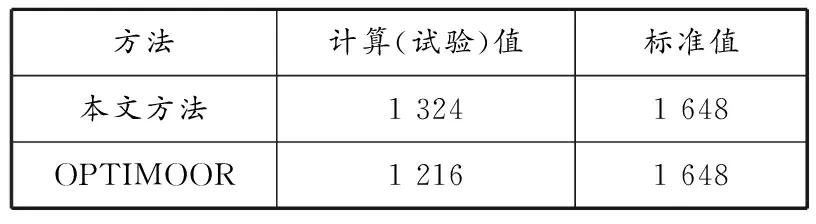
表6 护舷受力对比 单位:kN

从表4～6可知,本文计算结果与OPTIMOOR软件分析结果具有较强的一致性,这说明所建模型满足精度的要求,进而证明了使用船舶操纵模拟器能准确地模拟船舶系泊作业过程,得到真实可靠的计算结果。通常情况下计算值还会略大于OPTIMOOR软件的分析结果,这是因为OPTIMOOR软件是将风、浪、流对船舶的作用看作一个准静态问题考虑的,而船舶操纵模拟器实现了对环境的实时仿真。因此,基于船舶操纵模拟器的船舶泊稳条件试验方法具有一定的优越性。

4.6 大型滚装船泊稳分析

为能够精确地描述和分析大型滚装船在码头系泊时受到的风、浪、流的影响,以系泊船体运动量、系泊缆力、护舷反作用力等3项指标对其泊稳性进行评估,当系泊船体运动量小于规范值,最大系泊缆力小于允许的最大安全工作载荷,护舷反作用力小于其设计反力时,可以认为满足泊稳要求。

通过上述计算结果可以看出,在两种不同环境载荷作用下船舶在6个自由度上的运动量极值均未达到临界值,其各运动状态相对稳定,对船舶泊稳不会产生影响。两种计算工况下8根缆绳的最大张力均小于缆绳的破断载荷395 kN,因此在所有计算工况下该大型滚装船码头系泊方案均能够满足泊稳的要求。当风、浪、流等环境载荷共同作用时,大型滚装船存在向码头靠近的运动趋势,挤压码头护舷,但所有计算工况下护舷反作用力均小于护舷的设计反力,该护舷满足大型滚装船泊稳需求。由此得到大型滚装船泊稳条件,见表7。

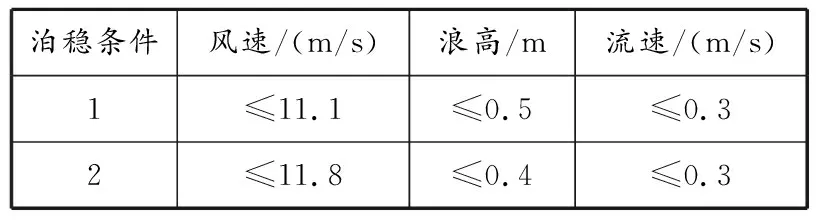
表7 4万t滚装船泊稳条件

为验证结果的合理性和准确性,改变环境参数重复进行泊稳试验。随着风速、浪高、流速的增加,船舶在各自由度上的运动量最大值增大,超过了允许的运动量,不能满足安全系泊作业要求;系泊缆力均有显著增大,超过了安全工作载荷,导致系泊缆绳断裂;最大护舷反作用力的变化规律与系泊缆力的相同,超过了护舷允许的反力标准值,船舶与码头之间发生剧烈的碰撞。因此,表7的泊稳条件可以作为船舶泊稳的极限环境条件,此时4万t大型滚装船的泊稳性能良好。如果实际海况劣于该海况,则整船安全会受到威胁,应停止作业。

5 结束语

基于MMG基础理论,充分考虑风、浪、流载荷的作用,考虑系泊缆绳的线性动态特性和船舶与护舷间的相互影响,建立了大型滚装船系泊运动的数学模型,为实现船舶操纵模拟器的功能拓展奠定了理论基础。所提基于船舶操纵模拟器进行泊稳条件试验的方法,具有较高的计算精度,不仅能够模拟环境的动态变化,同时还能准确地反映系泊船体及其系泊缆绳自身形态的变化情况,具有优良的实用价值和工程意义。

虽然对大型滚装船泊稳研究取得了较为理想的结果,但是所建立的系泊模型是基于随机风、规则浪和均匀流假设的,如何更详细地计入波浪力的影响,更精确地描述船舶在系泊作业时的运动数学模型还有待进一步研究。