轮履模式可切换的移动机器人建模与控制

梁志远,赵佳辉,李清都,陈媛媛

(1.上海理工大学 机器智能研究院,上海 200093;2.上海理工大学 光电信息与计算机工程学院,上海 200093;3.海军军医大学 海军军医系,上海 200433)

0 引 言

随着机器人技术的发展和广泛应用,移动机器人面临着更加复杂的环境。因此,能够实现快速移动、应对复杂地形、克服障碍的移动机器人是目前热门的研究主题[1-2]。

按照运动形式,移动机器人大致分为4类:足式、履带式、轮式和复合式[3]。虽然双足[4]、四足[5]机器人在克服障碍,爬楼梯等方面表现性能良好,但是以牺牲稳定性作为前提,控制器复杂需要大量的计算去执行动作,而且负载低,续航也短。相比之下,履带式机器人[6]依靠结构上的设计便能够轻松克服障碍,但是身体笨重、灵活性差、能效低、履带磨损大。轮式机器人[7]移动快、能效高、续航久,但一般无法处理崎岖地形,特别是超过轮子半径的障碍等情形。复合式机器人则将2种或2种以上运动形式结合在一起,2种常见的结合形式为轮足式和轮履式[8],可以兼具不同运动形式的优点,环境适应能力强,这使得复合式机器人成为移动机器人领域的热点之一。

近年来,复合式机器人的研究取得了不少成果。苏黎世联邦理工学院的双轮足式机器人Ascento[9]利用线性二次型调节器(linear quadratic regulator, LQR)来实现平地动态平衡控制,采用跳跃的方式克服障碍。四轮足式机器人ANYmal[10]利用模型预测控制(model predictive control,MPC)实现在陡峭的地面快速移动以及爬楼梯等复杂任务。传统轮履机器人采用结构叠加的方式来实现轮式与履带式的结合,而文献[11]的轮履式机器人,利用履带伸缩结构切换轮式与履带式运动。上述机器人均存在一些不足之处。Ascento和ANYmal采用腿式结构,负载能力差,复杂路面需要视觉辅助,盲适应性差。前者跳跃式越障牺牲系统稳定能力,无法应对崎岖地形;后者足式运动速度慢、控制器复杂、运动效率低。传统的变形轮履结构设计冗余复杂,不易扩展其他功能。文献[11]的伸缩机构则导致履带长度受限,车轮较大,车身较短,履带越障能力下降。

针对上述复合式机器人的不足之处,本文提出一种具有双轮平衡模式和履带模式的新型轮履移动机器人模型,其侧视图如图1所示。该机器人由车身、驱动轮和履带摆臂构成;采用轮履耦合结构,整体结构简单而紧凑;车身可以安装机械爪,配合车身执行抓取任务;履带摆臂包括履带、连杆和从动轮。机器人共有4个驱动电机,其中2个驱动左右驱动轮,另外2个驱动左右履带摆臂。

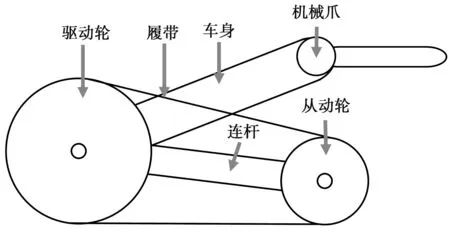
图1 机器人整体侧视图Fig.1 Concept of robot side view

本文机器人具有2种运动模式,可通过控制摆臂调整机器人质心,实现模式间切换:①双轮平衡模式,实现平坦路面快速移动,具有高能效和长续航的能力;②履带模式,应对复杂路面及障碍,且具有高负载能力。新型机器人融合轮式和履带式优点,地形适应性强,可用于执行巡检安防、勘探救援等任务。

目前,对于双轮平衡和履带式这类单一模式机器人的理论研究已较为成熟,本文针对具有双轮平衡和履带模式这一新型结构,在控制上实现不同姿态下的动态平衡和轮履模式的快速稳定切换,以提高机器人的地形适应能力。

1 机器人动力学建模

1.1 等效倒立摆模型

在双轮平衡模式下,轮履移动机器人的摆臂运动会改变机器人质心和平衡点位置,因此,可先将其等效为变质心倒立摆系统,使模型降阶,简化动力学方程。机器人倒立摆等效模型如图2所示,主要的模型参数如表1所示。

图2 平面倒立摆等效模型Fig.2 Equivalent model of inverted pendulum

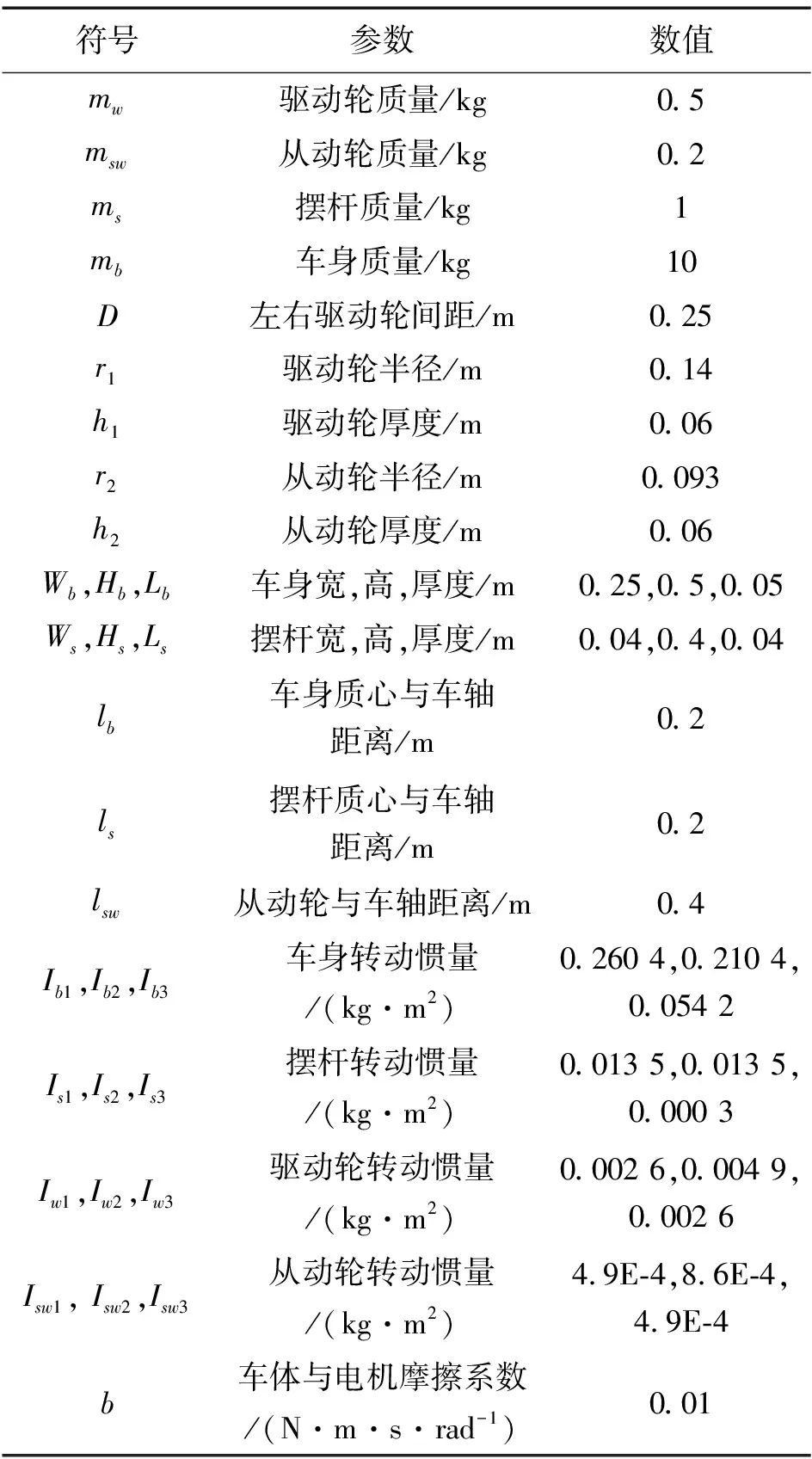
表1 机器人模型参数

本文定义如下参数。

{I}:惯性测量单元(IMU)坐标系。

{M}:固连在车轴上的机械坐标系。

αl,αr:左右摆臂相对前进方向的姿态角。

βl,βr:车身与左右摆臂的关节角。

θ0:不同摆臂关节角下机器人平衡点。

θl,θr:左右摆臂与等效倒立摆夹角。

θ,lc,mc:等效倒立摆俯仰角、质心距车轴距离、质量。

Ic1,Ic2,Ic3:等效倒立摆在其质心系下的转动惯量。

机器人摆臂由连杆、履带和驱动轮组成,其中履带质量忽略不计,摆臂质量为ma=ms+msw,摆臂质心距车轴距离为la=(msls+mswlsw)/(ms+msw),本文定义sθ=sinθ,cθ=cosθ,左右摆臂和车身质心在{M}下的位置为Rr=[lasθrlacθr],Rl=[lasθllacθl],Rb=[-lbsθ0lbcθ0]。

根据质点系定义得等效倒立摆质心位置为

(1)

机器人处于平衡点时,倒立摆质心位置在X轴的分量Rcx=0,质心距车轴距离则为在Z轴的分量,即lc=Rcz。

令θr=βr-θ0,θl=βl-θ0,可得平衡点θ0,质心距车轴距离lc分别为

(2)

令θr=π/2-αr,θl=π/2-αl,可得在期望摆臂姿态角αl,αr下的摆臂关节角逆解为

(3)

等效倒立摆质心的转动惯量Ic1,Ic2,Ic3可根据动能守恒推导出,假设机器人绕着坐标系Y轴以wy角速度转动,则倒立摆质心动能Ecy等于车身和摆臂的质点组动能Ey,表示为

(4)

(5)

记绕着X、Z轴的质心动能和质点组动能分别为Ecx,Ex和Ecz,Ez,可得

(6)

(7)

倒立摆质心的转动惯量Ic1,Ic2,Ic3与左右摆臂关节位置关系为

(8)

1.2 拉格朗日方程建模

轮履移动机器人经过变换后可以看作一个两轮倒立摆机器人,其原理如图3所示,俯视图如图4所示,其中,{W}为世界坐标系,{M}为固连在车轴中心的机械坐标系,{C}为位于倒立摆质心的质心坐标系。图3中部分参数定义如下。

γl,γr:左右驱动轮转动角度。

vl,vr:左右驱动轮线速度。

vm,vc:机械原点M和倒立摆质心线速度。

Tl,Tr:左右驱动轮力矩。

fl,fr:左右驱动轮阻尼力。

图3 倒立摆机器人原理图Fig.3 Schematic diagram of inverted pendulum robot

机器人运动过程由直线、俯仰和偏航运动共同组成[12],分别通过控制机器人位置x、俯仰角θ和偏航角φ来实现。为了完整描述机器人的运动,总共需要13个广义坐标:xm,ym,xl,yl,xr,yr,xc,yc,zc,γl,γr,θ,φ。对于参考系{W},每个刚体的质心位置为

xc=xm+lcsθcφ,yc=ym+lcsθsφ,zc=lccθ,

xl=xm-0.5Dsφ,yl=ym+0.5Dcφ,

xr=xm+0.5Dsφ,yr=ym-0.5Dcφ

(9)

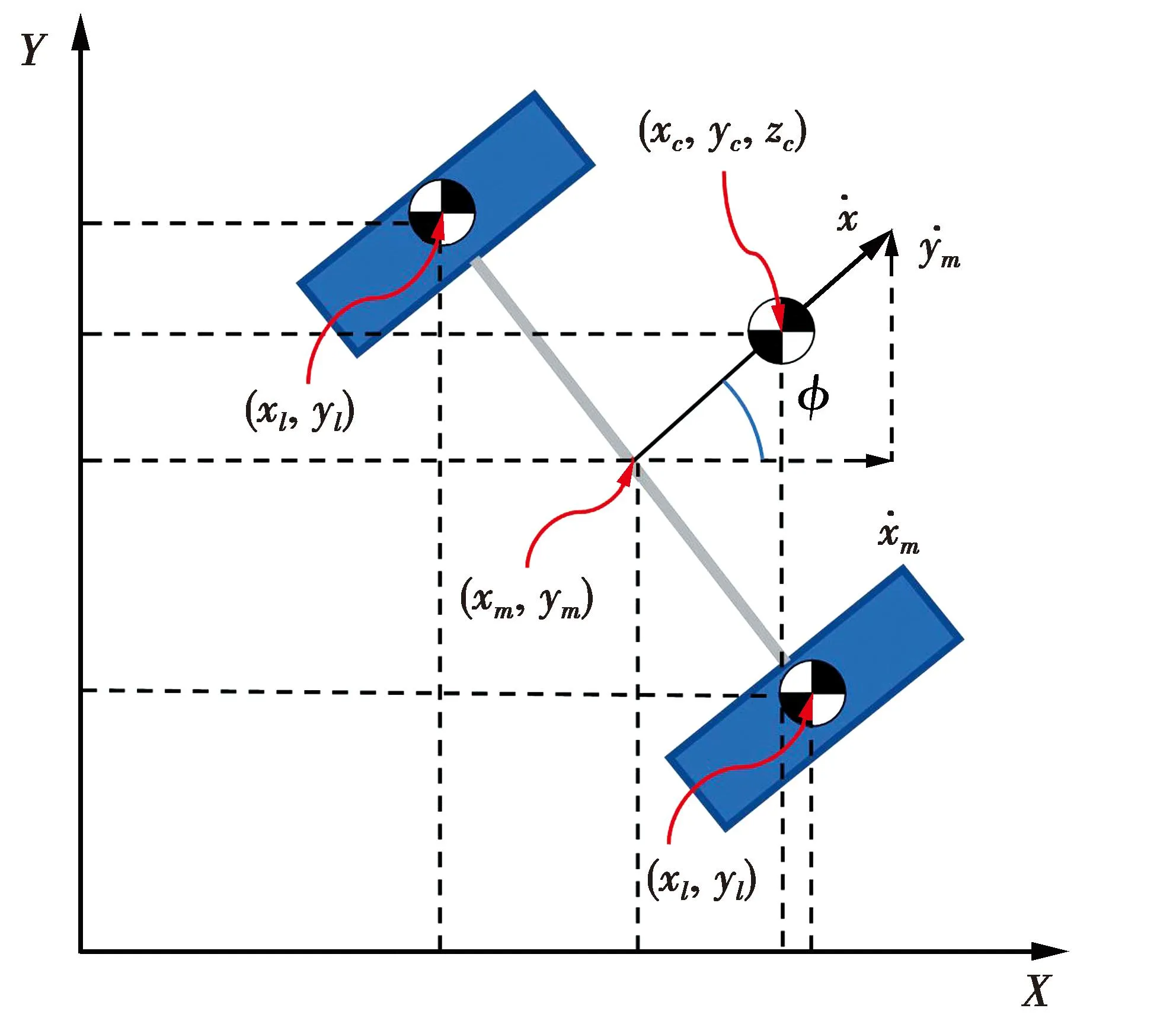
图4 机器人俯视图Fig.4 Top view of robot

假设机器人驱动轮运动时与地面无相对滑动[12],则机器人位移x和偏航角φ为

(10)

对(10)式微分后化简,得驱动轮角速度为

(11)

则从动轮角速度为

(12)

对(9)式微分后得到各个刚体的质心速度为

(13)

拉格朗日方法需要将机器人刚体的动能和势能表示为广义坐标的函数,机器人的平动动能可表示为

(14)

机器人的转动动能可表示为

(15)

(15)式中:第2项为倒立摆质心绕y轴的转动动能,考虑了倒立摆俯仰角θ的影响;第5项为从动轮的转动动能,这是因为在计算质心转动惯量时没有考虑从动轮自身转动。

当机器人在平面运动时,垂直运动仅与俯仰角θ有关,因此势能为

V=mcglccθ

(16)

拉格朗日函数定义为

L=Ttrans+Trot-V

(17)

机器人的广义坐标为位置x,俯仰角θ和偏航角φ,对应的广义力Fx,Fθ,Fφ可以表示为

(18)

则拉格朗日运动方程可表示为

(19)

将(11)—(18)式代入(19) 式可以得到机器人3个独立的非线性运动方程,表示为

(20)

(21)

(22)

1.3 状态空间方程

平衡模式下,机器人通常工作在平衡点附近。当俯仰角|θ|≤10°时,系统在平衡点处线性化后的状态方程与原非线性方程的误差很小[13],此时可以近似地认为sinθ≈θ,cosθ≈1,在忽略所有的二次项和交叉项后, (20)—(22)式可整理为

(23)

(24)

(25)

由(23)—(25)式,有

(26)

由线性化后的运动方程(24)—(26)式可看出,机器人位置x和俯仰角θ相互耦合,偏航角φ则相对独立,表现为机器人前后运动和俯仰角有关,转向运动独立[13],因此,可以将机器人的状态方程解耦为2个单独系统。

定义解耦后的2个系统输入转矩为Tx和Tφ,其中,Tφ=(Tr-Tl)/2。

则有

(27)

描述机器人前后运动的四阶系统的状态方程为

(28)

(28)式中:u1=Tx;C1为4×4单位矩阵;状态变量x1选取为机器人位移、速度、俯仰角度和角速度,表示为

(29)

描述机器人转向运动的二阶系统的状态方程为

(30)

(30)式中:u2=Tφ;C2为2×2单位矩阵;状态变量x2选取为机器人偏航角和角速度,表示为

(31)

当机器人处于默认姿态时,摆臂关节角βr=βl=0。由(2)式和(8)式可得,此时机器人平衡点θ0=0,质心高度lc=0.206 452 m,质心惯量Ic1=0.303 819 kg·m2,Ic2= 0.254 564 kg·m2,Ic3=0.055 684 9 kg·m2,代入参数后得

(32)

(33)

(34)

2 LQR控制器设计

本文机器人的开环系统在双轮平衡模式下具有明显的不稳定性,经计算得前后运动系统的特征值为[0,-0.905 14,-0.072 3,8.719 9],在平衡点附近是不稳定的。系统的完全能控性是反馈控制器设计的前提[14],系统能控性矩阵为

M=[BAB…AnB]

(35)

经分析可知,rank(M1)=4,rank(M2)=2,能控矩阵满秩,系统完全能控。

平衡模式下机器人需要一个稳定的控制器来保证其在保持平衡的同时,能够稳定前进、可动态调整摆臂姿态以及在轮履模式间进行平滑切换。机器人还应该能够处理外部干扰,同时应使用尽可能小的空间进行模式切换。为此,本文基于LQR方法设计控制器,这是一种能够以最小代价实现线性系统调节的最优控制策略,二次型最优函数为

(36)

(36)式中:Q是半正定矩阵,表示对x的每个状态的动态误差的惩罚程度;R是正定矩阵,表示对控制输出所消耗能量的惩罚[14]。

(37)

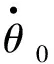
(38)

(38)式中,ep,wp分别为IMU的俯仰角度和俯仰角速度。

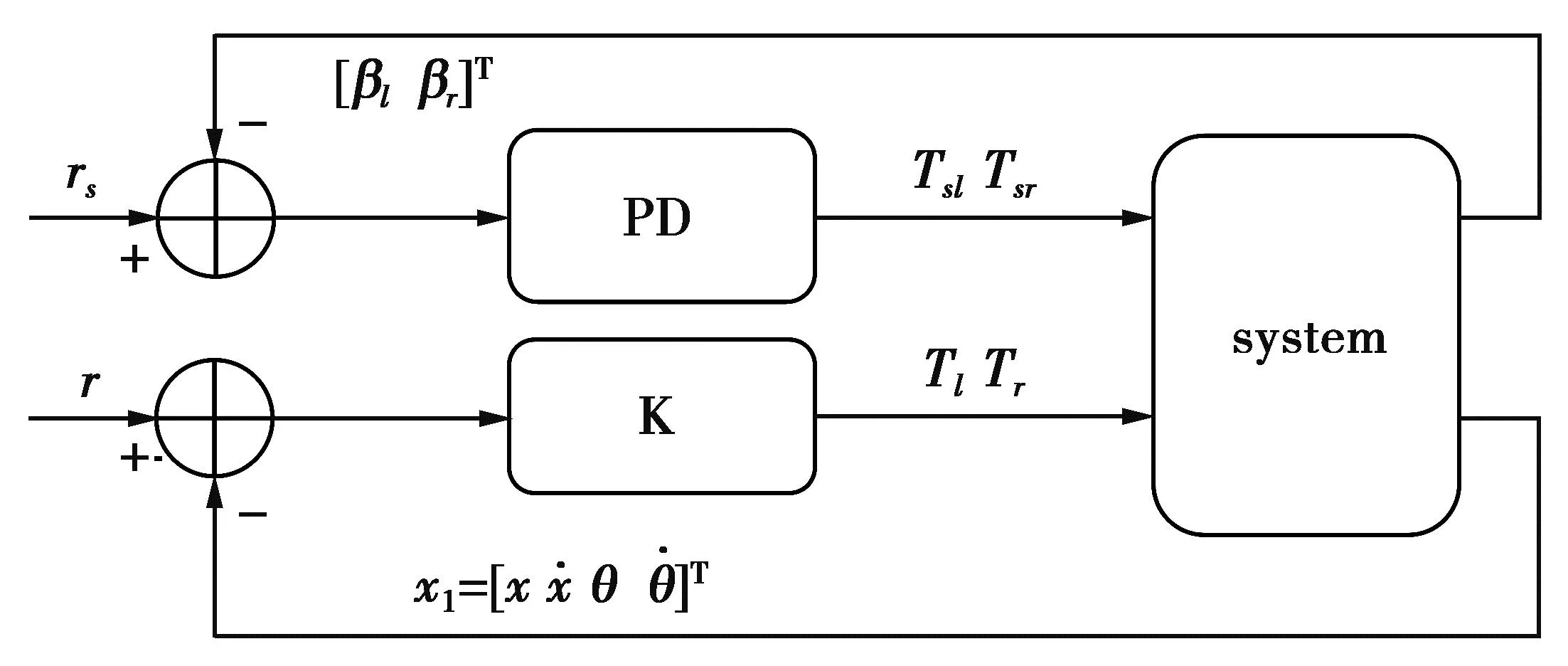
图5 系统控制回路Fig.5 Control loop of the system

3 实验与仿真分析

本文选用Webots仿真平台对机器人进行实时仿真。Webots是一款开源的机器人仿真软件,主要用于机器人建模、控制与仿真和验证机器人控制算法,其内核基于开源物理引擎(open dynamics engine,ODE),动力学仿真结果较为真实。本实验使用Webots自带的模型库、零件库等搭建了轮履移动机器人仿真模型,并对设计的控制器效果与轮履模式切换策略进行仿真验证。

3.1 阶跃响应

从图6可以看出,姿态补偿后的LQR控制器可以实现不同摆臂角度下参考指令的快速跟踪,且响应无超调,调节时间短。摆臂0°时,稳定时间约为6 s;摆臂90°时,稳定时间为约为5 s。这是因为在同一组控制器参数下,前者倒立摆质心到车轴距离lc=0.206 5,而后者lc=0.167 5,质心低,稳定快。

图6 不同摆臂位置阶跃响应下状态曲线对比Fig.6 Comparison of state curves under step response of different swing arm positions

3.2 履带摆臂控制

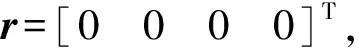
图7 摆臂周期运动时状态曲线对比Fig.7 Comparison of state curves during periodic motion of the swing arm

从图7可以看出,基于姿态补偿后的LQR控制器虽然不能完全消除摆臂运动带来的干扰,但从幅值上看状态数据波动很小,其中,位置x的振幅在±0.02 m之间,俯仰角θ的振幅在±0.007 4 rad之间,由此可以推断姿态补偿对摆臂运动的干扰有很强的抑制能力。

3.3 轮履模式切换

基于平衡点姿态补偿的LQR控制器经过验证可以实现摆臂运动时稳定的平衡控制,在此基础上加入一定的切换策略可实现模式切换。模式切换过程包括平衡到履带模式和履带到平衡模式。

图8为平衡到履带模式的切换过程。图8a机器人处于平衡模式下,此时为姿态补偿的LQR控制;图8b摆臂关节按5次多项式轨迹,在0～2 s时从0°运动到105°,使得摆臂接近地面,避免触地时冲击过大;图8c在2 s时退出平衡控制,驱动轮改为速度控制,并施加给驱动轮反向速度使得机器人前倾,摆臂与地面接触;图8d摆臂关节按5次多项式轨迹从105°运动到30°,完成模式切换。

图8 平衡模式到履带模式切换过程Fig.8 Switching process from balance mode to track mode

图9为履带到平衡模式切换过程机器人实时数据。从图9可以看出,在2 s时,机器人状态和驱动轮扭矩的抖动是由切换过程图8c中驱动轮反向速度引起的;2.72 s左右的数据抖动是由摆臂碰撞地面引起的,除此之外,整个切换过程都十分平稳。

图9 平衡到履带模式切换过程实时数据Fig.9 Real time data of the switching process from balance to track mode

图10为履带到平衡模式的切换过程。图10a机器人处于履带模式下,此时驱动轮为速度控制;图10 b摆臂关节按5次多项式轨迹,在0～2 s时从30°运动到105°,此时摆臂展开质心抬高,机器人状态进入控制器调节范围;图10c在2 s时将速度控制改为姿态补偿LQR控制,机器人进入平衡模式;图10d将摆臂关节按5次多项式轨迹从105°运动到0°,完成模式切换。

图10 履带模式到平衡模式切换过程Fig.10 Switching process from track mode to balance mode

图11为履带到平衡模式切换过程机器人实时数据。从系统状态和驱动轮扭矩可以看出,机器人在6 s内实现了平稳的运动模式切换。

图11 履带到平衡模式切换过程实时数据Fig.11 Real time data of the switching process from track to balance mode

综上所述,本文提出的新型轮履移动机器人在基于平衡点姿态补偿的LQR控制器下具有良好的动态平衡控制性能,对摆臂运动具有较强的抗扰能力,该方法能够满足轮履模式快速稳定切换的要求,在6 s内实现模式切换,使机器人可以充分发挥轮式和履带式的优势,灵活适应不同环境。

4 结束语

针对目前复合式移动机器人存在的缺陷,本文提出一种具有双轮平衡和履带2种模式的轮履复合式机器人,其结构简单紧凑且兼具轮履2种模式优点,为复合式机器人研发提供另一种思路。针对这一新型轮履机器人结构,采用基于姿态补偿的LQR方法设计了平衡控制规律,实现不同摆臂角度下对参考位置的无超调快速响应。仿真结果表明,该控制器对摆臂运动造成的状态扰动有很强的抑制能力,且能够实现轮履模式快速稳定切换,提升了机器人机动性能,使其可于城市地区巡检安防、灾区勘探救援、辐射环境监测等任务。