基于mRMR和CCA的AD分类方法研究
2023-12-29张国栋董爱美齐志云刘思迪
张国栋,董爱美,齐志云,刘思迪
齐鲁工业大学(山东省科学院) 计算机科学与技术学部,山东 济南 250353
阿尔茨海默病(AD)是一种起病隐匿、进行性发展的神经退行性疾病,多见于65岁以上人群,主要影响患者脑功能,临床表现主要包括记忆力减退、语言障碍、空间定向能力下降、行为和情绪变化以及认知障碍等[1]。目前对AD并无有效的治疗手段,只能寄希望于能够尽早识别出AD患者并及时干预治疗。轻度认知障碍(MCI)是AD的早期阶段,对MCI患者进行有效治疗可以延缓病情进展甚至促进康复,因此,若能尽早识别出MCI患者,将有助于患者接受治疗,防止病情恶化。
随着人工智能的蓬勃发展,各种改进的机器学习方法开始广泛应用于AD的分类研究中,为使用神经影像数据辅助医生进行AD诊断做出了巨大贡献。在进行AD分类的研究中,有些学者关注于单一模态图像的应用,如核磁共振成像(MRI)[2]、正电子发射断层扫描成像(PET)[3]和弥散张量成像(DTI)图像[4]等,这些图像技术在研究中可以提供丰富的信息,如脑结构、脑代谢和脑连接等方面的特征。Uysal等[5]根据年龄、性别和左右海马体积值创建了一个数据集,然后通过使用机器学习技术对海马体积信息进行分类,实验证明 MRI图像可用于区分AD、MCI 和正常对照组(NC)。Fan等[6]提出了一个U-net模型,用于使用MRI图像进行AD分类。Ji等[7]将MRI图像的灰质和白质图像切片作为输入数据,使用卷积神经网络(CNN)进行AD分类,在AD与NC的分类实验中取得了88.37%的准确率。Chen等[8]结合MRI图像和临床特征构建 Stacking 框架,在AD多分类任务中平均准确率达到了86.96%。Al Shehri[9]提出使用DenseNet-169和ResNet-50 CNN架构对AD进行诊断和分类,实验结果表明,DenseNet-169 架构表现出色,准确率达到了83.83%,而ResNet-50 的准确率为81.92%。
但是,只使用一种模态数据进行分析势必会造成信息的不充分,从而影响整体的AD分类准确率。因此,一些研究学者开始整合来自多种模态的神经影像数据,以提高AD分类的分类性能。Huang等[10]使用CNN融合MRI和PET数据以提高AD分类准确率。Lin等[11]构建了用于AD分类的3D可逆生成对抗网络(GANs)。Cosmo等[12]提出了一种新的端到端的可训练图学习框架,用于动态和局部图修剪。该方法可以在提高AD分类精度的同时降低网络结构的复杂度,提高模型运行速度。Huang等[13]提出了一个可以自动整合多种神经影像数据和非影像数据的通用框架,不仅在AD分类中取得了很好的分类效果,还可以用于自闭症谱系障碍和眼病预测。Jiang等[14]在全卷积网络模型中添加外部注意力模块,同时引入Softmax和L1范数的双重归一化方法,以获得更好的分类的性能和更丰富的特征信息疾病概率图,在AD分类任务中,该方法取得了92.36%的分类准确率。
虽然现有的方法在AD分类中取得了令人满意的结果,但仍存在着一定缺陷:首先,多模态神经影像数据在预处理后仍然存在样本量小、维数高的问题,限制了模型的分类性能;其次,部分研究只使用了单模态数据,没有充分利用多模态数据的潜在信息,限制了分类效果。为解决以上两个问题,本文提出了一种基于mRMR和CCA的AD分类方法(mRMR-CCA)。相较于其他方法,该方法具有两个优点:(1)对多模态神经影像数据进行特征选择,去除了冗余信息;(2)挖掘多模态数据间的内在联系,充分利用多模态互补信息进行AD分类。
1 方法
1.1 最大相关-最小冗余算法
特征选择可以分为两个过程:(1)怎样度量特征相关性。(2)怎样解决特征之间的冗余。互信息是一种能够度量两个变量之间相关性的指标,不仅可以考虑线性关系,还能考虑非线性关系,定义两个变量X和Y之间的互信息如下:
其中,p(x,y)是联合分布,p(x)和p(y)是边际分布,互信息I(X;Y)则为联合分布和边际分布的相对熵。
为了解决特征选择中的相关性和冗余问题,研究学者提出了一种基于互信息理论的特征选择方法,即最大相关-最小冗余算法(mRMR),该算法的实现基于两个关键条件:最大相关性条件和最小冗余条件。
最大相关性条件旨在寻找与样本类别信息相关性最大的特征子集,通过最大化特征与类别之间的互信息来选出与类别预测最相关的特征,目标函数如式(2)所示:
最小冗余条件旨在寻找最小化特征之间重叠信息的特征子集,通过最小化特征之间的互信息,可以确保所选的特征不会包含任何冗余信息,目标函数如公式(3)所示:
其中,S代表特征子集,c为类别标签。
结合最大相关和最小冗余这两个条件,可以得到mRMR的目标函数如下所示:
1.2 典型相关性分析算法
典型相关性分析算法(CCA)通过寻找几组合适的映射方向来研究少数几组变量的相关性,从而揭示两种模态数据间的内在相关性。具体而言,假设有n个样本,每个样本有两种模态数据,每种模态数据都包含d个特征,则第一种模态数据可以表示为矩阵X={x1,x2,…,xn}∈d×n,第二种模态数据可以表示为矩阵Y={y1,y2,…,yn}∈d×n。CCA采用搜索出的两组典型变量wx∈d和wy∈d,使线性组合和之间的相关系数最大,即求解相关系数的最大值,如式(5)所示:
其中,Cxy=XYT为X和Y之间的互协方差,并且Cxy=CTyx,Cxx=XXT和Cyy=YYT分别为特征矩阵X和Y的方差。为保证解的唯一性,对该问题采取固定分母,将分子的优化作为目标的方式,从而将该问题转化成一个凸优化的问题,故该目标函数可以转化为:
对于上述优化问题,通常采用特征值分解的方法进行求解。
首先,利用拉格朗日乘子法,将式(6)转化为以下目标函数:
其中,λ和θ代表拉格朗日乘子。分别对wx、wy求偏导数,并令偏导数为0可得:
Cxywy-λCxxwx=0, (8)
Cyxwx-θCyywy=0, (9)
分别将式(10)和式(11)互相代入,可得:
在得到新的特征矩阵后,将两组不同模态的特征融合成一组新的特征矩阵,这组特征矩阵包含了两组数据的相关性信息,可以更好地反映数据之间的关联。通常采用以下两种方式进行多模态特征融合,若采用相加融合的方式,得到的融合特征表示为:
若采用连接融合的方式,得到的融合特征表示为:
1.3 方法介绍
为去除多模态数据的冗余信息并充分利用不同模态间的互补信息,提出基于mRMR和CCA的AD分类方法(mRMR-CCA),该方法主要分为3个步骤:(1)特征选择;(2)特征融合;(3)AD分类。具体来说,首先使用mRMR算法从每个模态中选择出更有助于分类的判别性特征,之后采用CCA算法对多模态数据进行特征融合,在融合过程中采取连接的融合方式,形成一个包含更多互补信息的新的特征集合,以提高分类性能,最后,采用SVM分类器进行分类。详细过程如图1所示。

图1 mRMR-CCA方法流程图
2 数据集及预处理
2.1 数据集
阿尔茨海默病神经成像研究计划(ADNI)[15]旨在寻找与AD相关的疾病标志物,并为早期AD的诊断和追踪提供支持的神经影像研究计划。目前,ADNI研究计划已经进行了4个阶段的研究(ADNI-1、ADNI-GO、ADNI-2、ADNI-3),其中每个阶段都招募了大量的参与者,采集了大量的临床和影像数据。
实验使用了来自ADNI数据库的156名受试者的MRI和PET神经成像数据来研究AD分类问题,其中包括3组人群,即AD患者组、MCI患者组和NC受试者组,每组均包括52名受试者。表1提供了这些受试者的详细信息,包括每个类别的人数、年龄、MMSE评分[16]和CDR评分[17]。根据阿尔茨海默症和相关疾病协会的标准,NC组受试者的MMSE评分为24~30分,CDR评分为0;MCI组受试者的MMSE评分为24~30分,CDR评分为0.5;AD组受试者的MMSE评分为20~26分,CDR评分为0.5或1。

表1 受试者的统计信息
2.2 预处理
从ADNI数据库下载了MRI图像和PET图像。对于MRI图像,ADNI执行了梯度不均匀性校正以控制图像质量,之后,进一步对数据进行预处理。预处理操作可以分为两部分:一是图像处理,二是特征提取。图2展示了使用SPM工具[16]对MRI和PET两种图像的预处理过程。

图2 MRI和PET的预处理工作流程
对MRI图像的预处理主要包括图像校准、图像分割、空间标准化和平滑等操作。具体来说,首先进行前连合-后连合(AC-PC)校正,使得不同个体的数据可以进行比较和分析。其次,利用组织概率模板(TPM)可以将MRI图像分割成灰质、白质和其他区域,同时可以将灰质和白质图像映射到MNI空间,保证所有的样本都处于到同一坐标系统中。然后,在空间标准化时,使用李代数微分同胚配准算法(DARTLE)方法,该方法通过创建群组平均的灰质和白质图像,制作平均模板图像,之后利用该图像实现原始灰质图像的空间标准化处理。最后,使用8 mm平滑内核进行平滑以去除噪声。对于PET图像,首先将96张DICOM格式的图片合并成一张3D PET图像,其次利用配准技术使每个受试者的PET图像与其对应的T1 MRI原始图像对齐,然后进行头部运动校正和空间标准化,最后完成平滑操作。
在特征提取中,使用RESTPlus[18]工具。首先将MRI和PET图像重新采样到与解剖自动标记(AAL)模板[19]相同的大小,即61×73×61。之后,对于MRI图像,提取对应于90个感兴趣区域的平均体积值,提取PET图像的90个感兴趣区域的平均强度值。
3 实验及结果分析
3.1 实验设置
本文进行了3个二元分类任务来验证mRMR-CCA的有效性,包括(1) AD vs.NC;(2) MCI vs.NC;(3) AD vs.MCI。此外,使用准确率(ACCU)、ROC曲线下面积(AUC)、灵敏度(SENS)和特异性(SPEC)4个指标来评估分类器的性能。其中,ACCU表示所有样本被正确分类的概率,SENS表示正确分类的正例样本占所有正例样本的准确率,SPEC衡量模型在预测反例时的准确率。在AD vs.NC和MCI vs.NC分类任务中,将NC视为正样本,将AD和MCI视为负样本。在AD vs.MCI的分类任务中,将MCI视为正样本,将AD视为负样本。在每个实验中,使用LIBSVM工具箱[20]中的SVM分类器作为实验的分类器。值得注意的是,在SVM分类器中使用了RBF核函数,主要原因是该函数对数据中的噪声有很好的抗干扰能力。其次,使用非线性核函数可以获得更好的结果。
3.2 消融实验
在本实验中,比较了mRMR-CCA方法和单独使用mRMR算法或CCA算法这两种独立算法的方法,以评估它们对AD分类性能的影响,并且通过表2展示了它们之间的差异。在表2中,用“粗体”对最佳分类结果进行了标注,对使用到的算法使用“√”进行了标记。其中,CCA使用连接融合的方式将多模态数据进行特征融合,mRMR在对两个模态数据分别进行特征选择后,同样使用直接连接的方式将两个特征集合进行融合。CCA和mRMR算法均有标记的为本文提出的方法,即mRMR-CCA。
从表2可以看出,本文提出的mRMR-CCA方法在3个二分类任务中取得了最好的分类性能,而只使用CCA进行两种模态数据的特征融合所取得的分类性能最差。这是因为CCA虽然考虑了多模态数据间的内在联系,可以发挥出互补信息的作用,但是仍然存在冗余特征,这些冗余特征所含有的干扰信息降低了分类性能。而mRMR虽然能够从多模态数据中各自选出与标签最相关的特征,但是从本质上讲是分别对各模态数据进行的特征选择,后续再直接将多模态数据特征进行连接融合,存在丢失多模态数据互补信息的问题,从而导致分类效果不理想。
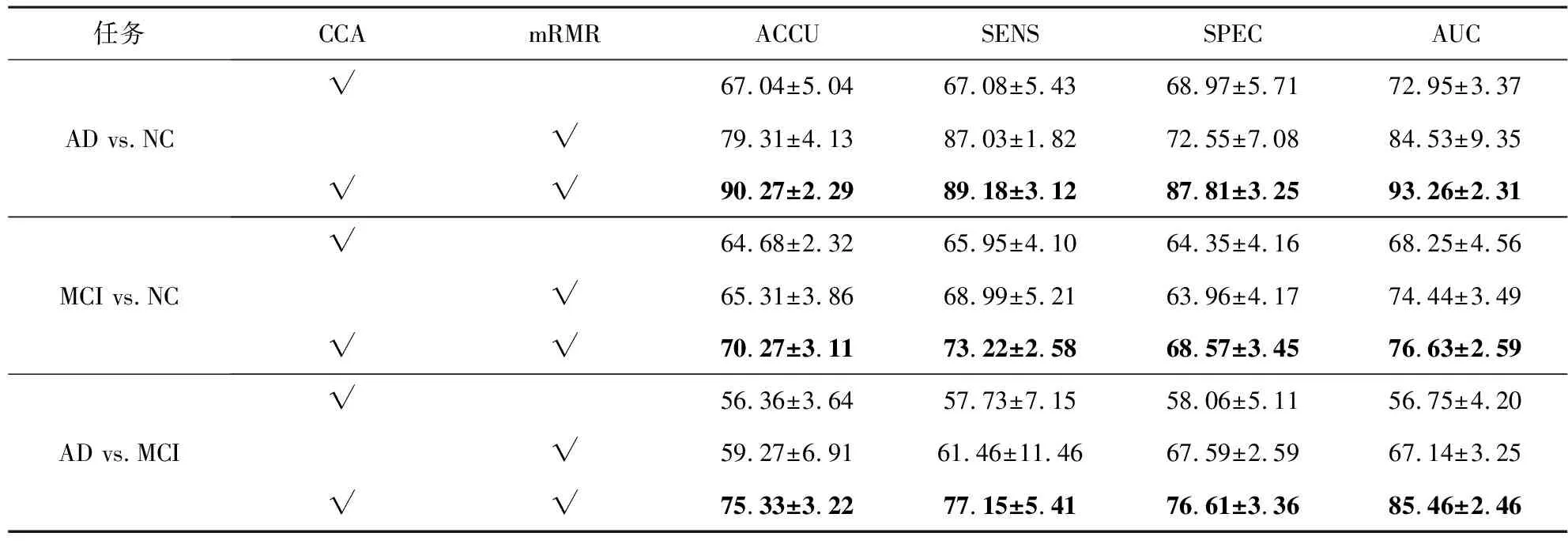
表2 消融实验 单位:%
提出的方法充分克服了这两个问题,首先使用mRMR算法去除了各个模态数据中的冗余信息,选择出了与分类标签存在最大相关性的特征,然后再通过CCA来充分挖掘多模态间存在的互补信息,形成一个新的特征集合,从而使分类性能得到了提升。
3.3 不同融合方法的对比
为了验证基于CCA的多模态融合方式在算法框架中的有效性,选择将mRMR算法选择出的两种模态的特征采取串行、并行的融合方式作为比较方法。此外,基于CCA的模态融合方法也有两种,即连接融合和相加融合的方式,同样比较了这两种融合方式的在AD分类问题上的性能差异,来验证在使用CCA算法基础上进行连接融合的方法的有效性,实验结果如表3所示。
从表3可以看出,本文提出的方法在3个分类任务中均取得了最好的结果。同时,直接对多模态数据进行串行或并行的特征融合方式所取得的分类效果并不理想,尤其是在MCI vs.NC的分类任务中,分类准确率低于63%。这主要是因为直接将两个模态的特征集合进行并行或串行融合,并不能很好地挖掘数据中的互补信息和共性特征,反而会导致出现信息相互干扰的问题,从而导致分类性能下降。而本文提出使用CCA算法进行特征融合,更多的考虑了多模态数据间的内在联系,使得两种模态数据集的相关性得到了提升,形成了包含更多互补信息的特征集合,从而提高了分类准确率。
此外,在使用CCA算法进行特征融合时,可以发现连接融合要比相加融合所取得的分类性能要好。这主要是因为相加融合更适合两个数据特征具有相同分布的情况,而多模态数据所具有的特征并不具有相同分布,所以相加融合会出现信息损失的问题,从而导致模型分类性能降低,甚至失效。相反,连接融合选择将两个数据特征进行拼接,虽然这种融合方式会出现维度增加和运行时间稍长等问题,但能够保证信息完整,使新的特征集合具有多模态数据中的全部互补信息,从而取得更好的分类结果。

表3 不同特征融合方式的对比 单位:%
3.4 不同方法的对比
为检验本文提出的算法在AD分类问题上的有效性,将mRMR-CCA与其他方法进行了对比,分类对比结果如表4所示。
其中,局部保持投影(LPP)、主成分分析(PCA)以及低秩表示(LRR)[21]3种算法属于特征选择方法,首先使用这3种算法分别对各模态数据进行特征选择,然后将选择后的特征进行连接融合。Xu等[22]提出了一种多视图混合嵌入方法(MvHE ),该方法采用分治法的策略来解决多视图数据中存在的差异性和非线性问题。You等[23]提出了多视图公共分量鉴别分析(MvCCDA ),以联合方式处理视图差异、可分辨性和非线性等问题。低秩公共子空间(LRCS)[24]寻求一个公共的低秩线性投影来缓解不同视图之间的语义鸿沟,LRCS能够跨不同视图捕获兼容的内在信息,并且还能够很好地对齐来自不同视图的类内样本。这3种多视图方法在多视图公共数据集上都取得了很好的分类效果,所以将这些多视图的理论方法应用于AD分类问题。针对AD分类问题,Prajapati等[25]设计了一个具有全连接层的深度神经网络(DNN)来执行二分类任务,隐藏层使用三种不同类型的激活函数,通过组合不同的激活函数来获得性能最佳的模型。
从表4中可看出,提出的方法在3个分类任务中均取得了不错的分类性能。与3种特征选择方法相比,提出的方法有显著提升,特别是在AD vs.NC分类任务中,提出的方法使得ACCU提高了40%,SENS提高了23%,SPEC提高了24%,AUC提高了27%,这表明本文方法在区分AD患者和正常人方面表现得更加出色。与3种多视图理论学习方法相比,提出的方法在AD vs.NC分类任务中性能略低于MvHE算法,但在其他两个分类任务中表现更出色,特别是在MCI vs.NC分类任务中,ACCU达到了70.27%,SENS达到了73.22%,SPEC达到了68.57%,AUC达到了76.63%。这说明提出的方法能够有效地识别MCI患者,有助于早期治疗,防止病情进一步恶化。与DNN算法相比,mRMR-CCA在MCI vs.NC分类任务中,准确率要稍差。但在其他3个指标上,提出的方法性能要更好,另外,DNN算法要求的样本数量较多,运行速度较慢。所以,综合来看,mRMR-CCA在AD分类问题上具有更好的性能,具有一定的有效性。

表4 不同方法的对比 单位:%
3.5 不同特征选择数目的对比
在mRMR-CCA方法中,首先使用mRMR算法进行特征选择操作,因此特征数目的多少对分类性能会有不同程度的影响。为了探究应该从各个模态中选择多少维特征进行AD分类,使用不同数量的特征进行分类,并观察准确率的变化趋势。图3呈现了准确率的变化趋势,其中mRMR维数以5的间隔从5变化到40。

图3 不同特征选择数目的对比
从图3可看出,在AD vs.NC和AD vs.MCI两个分类任务中,随着mRMR维数的增加,准确率呈现出先上升后下降的趋势。在AD vs.NC分类任务中,当特征维数为10时,取得的分类准确率最高;在MCI vs.NC分类任务中,当特征维数为5时,取得的分类准确率最高;在AD vs.MCI分类任务中,最高准确率出现在mRMR维数为10的时候。这表明选择不同数量的特征对不同的分类任务影响不同,需要根据具体的任务来选择合适的特征数量。此外,可以看到在所有分类任务中,mRMR维数达到一定程度后,准确率都会开始下降,这可能是由于过多的特征会引入噪声和冗余信息,从而降低分类性能。
实验结果表明,在mRMR-CCA方法中,特征数目的选择对于AD分类具有重要影响。在不同的分类任务中,需要根据具体情况选择合适的特征数量,以获得最佳的分类性能。
4 总 结
本文提出了一种基于mRMR和CCA的AD分类方法,旨在利用多模态数据之间的互补信息并消除冗余信息,提高AD的分类准确性。该方法首先使用mRMR算法从各个模态数据中选择出最有助于分类的特征,然后使用CCA算法将各个模态的判别性特征进行连接融合,形成一个新的融合特征矩阵,最后,将该矩阵输入到SVM分类器中进行AD分类,最终分类结果通过ACCU、SENS、SPEC、AUC 4个指标进行评价。实验证明,提出的方法在AD分类问题上具有一定的有效性。在未来的工作中,我们期望开发一种方法,将不完整模态数据用于 AD 分类问题,降低AD数据量不足的影响。
