Square-root parametrization of dark energy in f(Q) cosmology

M Koussour ,N Myrzakulov ,Alnadhief H A Alfedeel ,E I Hassan ,D Sofuoğlu and Safa M Mirgani

1 Quantum Physics and Magnetism Team,LPMC,Faculty of Science Ben M’sik,Casablanca Hassan II University,Morocco

2 L.N.Gumilyov Eurasian National University,Astana 010008,Kazakhstan

3 Ratbay Myrzakulov Eurasian International Centre for Theoretical Physics,Astana 010009,Kazakhstan

4 Department of Mathematics and Statistics,Imam Mohammad Ibn Saud Islamic University (IMSIU),Riyadh 13318,Saudi Arabia

5 Department of Physics,Faculty of Science,University of Khartoum,PO Box 321,Khartoum 11115,Sudan

6 Centre for Space Research,North-West University,Potchefstroom 2520,South Africa

7 Department of Physics,Istanbul University Vezneciler 34134,Fatih,Istanbul,Turkey

Abstract This paper is a parametrization of the equation of state (EoS) parameter of dark energy (DE),which is parameterized using square-root(SR)form i.e.,where ω0 and ω1 are free constants.This parametrization is examined in the context of the recently suggested f(Q)gravity theory as an alternative to general relativity (GR),in which gravitational effects are attributed to the non-metricity scalar Q with the functional form f(Q)=Q+αQn,where α and n are arbitrary constants.We derive observational constraints on model parameters using the Hubble dataset with 31 data points and the Supernovae (SNe) dataset from the Pantheon samples compilation dataset with 1048 data points.For the current model,the evolution of the deceleration parameter,density parameter,EoS for DE,and Om(z)diagnostic have all been investigated.It has been shown that the deceleration parameter favors the current accelerated expansion phase.It has also been shown that the EoS parameter for DE has a quintessence nature at this time.

Keywords: cosmology,dark energy,f(Q) gravity,EoS parameter

1.Introduction

Observational evidence for high redshift Supernovae (SNe)supports the growing idea of late-time cosmic acceleration[1,2].This observation is further supported by evidence of Baryon acoustic oscillations(BAO)[3,4],cosmic microwave background (CMB) [5,6],and large scale structure (LSS)[7,8].One of the most delicate difficulties in current cosmology is determining who is accountable for late time cosmic accelerated expansion.Our Cosmos/Universe is governed by an unidentified type of energy known as Dark Energy (DE).Although the inclusion of DE as the cosmological constant,has been exceedingly efficient,theoretical difficulties of fine-tuning and cosmic coincidence have hampered its effectiveness [9,10] .This leads physicists to describe the Cosmos with a phase transition from deceleration to acceleration.The kinematic method is explored by Turner and Riess to describe cosmic acceleration without assuming the validity of general relativity (GR) [11].This method has no influence on the physical or geometrical features of DE and is referred to as the model-independent way to investigate DE,i.e.via a parametrized equation of state (EoS) parameter of DE as a function of scale factor or redshift,and then comparing such parametrizations to cosmological data.Reference[12] is a review of the parametrization of the EoS parameterω(z).Another model-independent way to investigate the DE is to parametrize the deceleration parameter.For a quick overview of the deceleration parameter,see here [13].Nojiri and Odintsov also investigated numerous parametrizations of the Hubble parameter to study future cosmological singularities[14].The advantage of the parameterization method is that the result is independent of any specific gravitational theory.The negative is that it will not provide much direct knowledge on what is causing the Cosmos to accelerate.

Another approach to solving the late time acceleration problem and describing the origin of DE is to modify the action of GR,which is known as modified theories of gravity(MTG).Many modified theories have been suggested up to this moment.The f(R)gravity(where R is the scalar curvature)introduced by Buchdahl is the most important and extensively utilized modification to GR [15].Numerous researchers have examined various aspects of f(R)gravity and how it might induce cosmic inflation and acceleration [16–18].Another extension of the Einstein–Hilbert action is the presence of non-minimal interaction between matter and geometry.Thus,the so-called f(R,T)modified theory of gravity emerges.Harko et al introduced f(R,T) gravity theory,where the gravitational Lagrangian is characterized by an arbitrary function of the scalar curvature R and the trace of the energy-momentum tensor T [19].In f(R,T)gravity,several astrophysical and cosmological consequences are studied [20–24].Apart from curvature,the essential items involved with the manifold’s connection defining gravity are also torsion and non-metricity[25].The gravity theories may be divided into three categories based on the connection used.The first employs curvature,free torsion,and metric-compatible connections,such as GR.The second class employs a metriccompatible,curvature-free connection with torsion,such as the teleparallel equivalent of GR [26].The latter employs a curvature and torsion-free connection that is not metric compatible,for example,the symmetric teleparallel(ST)equivalent of GR[27].The geometrical trinity of gravity refers to these three equivalent interpretations based on the three separate connections[25].The f(Q) gravity (where Q is the non-metricity scalar) is a generalization of the ST equivalent of GR with zero torsion and curvature [28].Much research on f(Q) gravity has recently been published.[29,30]include the very first cosmological solutions in f(Q)theory,whereas[31,32]contain f(Q)cosmography and energy conditions.A power-law model has been examined using quantum cosmology [33].Cosmological solutions and matter perturbation growth index have been examined for a polynomial form of f(Q)theory[34].Harko et al used a power-law function to analyze the coupling matter in f(Q) gravity [35].

In this paper,we consider the square-root (SR) parametrization ofωDE(z),and then we use observational data to determine the behavior of the EoS parameter for DE.After confirming that the Cosmos underwent acceleration,we presume that the acceleration was caused by DE and employ a basic DE parametrization to investigate the property of DE within the framework of f(Q) gravity.The observational constraints on the model parameters are achieved by utilizing the most recent Hubble dataset with 31 data points,and SNe dataset from Pantheon samples compilation dataset with 1048 data points.Using the estimated values of model parameters,we examined the evolution of the deceleration parameter and the EoS parameter for DE at the 1-σ and 2-σ confidence levels.This study is structured as follows:in the next section,we describe the fundamental cosmological scenario of f(Q)gravity and derive the field equations in flat FRW space.Section 3 presents the parametrization model of the EoS parameter and the background for discussing the cosmic evolution of the Cosmos.In section 4,we have detailed the most recent observational data-sets used in our research.Section 5 goes with cosmological parameters such as deceleration parameter,energy density,EoS parameter,and Om(z)diagnostic.The last section contains the outcomes.

2.f(Q) cosmology

In f(Q)theory,the covariant derivative of the metric tensor is non-zero,and this fact can be represented mathematically in terms of a new geometrical variable known as non-metricity i.e.Qσμν=∇σgμν.So,f(Q) gravity is a modified theory that extends Einstein’s theory of GR by adding a function of the non-metricity tensor Q into the action,which has no curvature or torsion.The non-metricity tensor measures the variation of a vector’s length in parallel transport and is the critical geometric variable that explains the characteristics of gravitational interaction.The action of the f(Q) gravity is [28]

where Q is replaced by f(Q) in the symmetric teleparallel action,f(Q) being an arbitrary function of Q.Here,g is the determinant of the metric tensor gμνandLmis the usual matter Lagrangian density.The two independent traces of Qαμνare

Moreover,the non-metricity scalar is defined as a contraction of Qαμνgiven by

where Pσμνis the superpotential tensor (also known as the non-metricity conjugate) and

A variation of action(1)with regard to the metric gives the field equations as

We consider that the matter of the Cosmos is a perfect fluid with no viscosity.The energy-momentum tensor Tμνis given by

where uμis the 4-velocity satisfying the normalization condition uμuμ=-1.Also,ρ and p are the energy density and isotropic pressure of a perfect fluid,respectively.The current objective is to investigate the dynamics of the Cosmos against the background of the spatially flat Friedmann–Lemaitre–Robertson–Walker (FLRW) metric,which is expressed as

In this case,the non-metricity scalar is given by Q=6H2,whereis the Hubble parameter with a(t) as the scale factor and the dot is the derivative with respect to cosmic time t.The modified Friedmann equations govern the Cosmos’s dynamics take the form [29]

For f(Q)=Q,we get the standard Friedmann equations[29],as predicted,because,as previously stated,this specific option for the form of the function f(Q) represents the theory’s ST equivalent of GR limit.By using f(Q)=Q+F(Q),the field equations (8) and (9) can be written as

Equations (10) and (11) can be interpreted as the ST counterparts of GR cosmology,but with the inclusion of an additional component arising from the non-metricity Q of space-time that exhibits properties similar to those of a fluid component attributed to DE i.e.ρQ=ρDEand pQ=pDE.

Therefore,using equations (10) and (11),we obtain

where ρDEand pDEare the density and pressure contributions of the DE due to the non-metricity of space-time defined by

Furthermore,the equation of state(EoS)parameter due to the DE component is

By applying the covariant divergence to the field equations (5),we derive ∇μTμν=0 [36],and incorporating equation (6),the conservation equation for the energymomentum tensor can be derived as

3.Square-root (SR) parametrization for EoS parameter

For our investigation of SR parametrization,we pressume the functional formF(Q)=αQn,where α and n are model parameters.This specific functional form of f(Q) is motivated in [30].Also,we observe that if n=0,the model reduces to the standard ΛCDM model,withbehaving as the cosmological constant [37,38].The scenario n=1 corresponds to the symmetric teleparallel equivalent of GR,due to a factor of α+1 rescaling of Newton’s gravitational constant [29].Nevertheless,modification from the GR evolution occurs in the small curvature phase for n<1 and modification at the large curvature phase for n>1.Thus,whereas models with n>1 will apply to the early Cosmos,models with n<1 will apply to the late time DE-dominated Cosmos [30].

Using this form,we derived the energy density ρDE,and pressure pDEfor DE in terms of Hubble parameter as,

To get cosmological findings that enable for direct comparison of predicted results with observational data,we include the redshift parameter z,expressed byas an independent variable instead of the cosmic time variable t.Here,we have normalized the scale factor so that its current day value is one i.e.a(0) =a0=1.Therefore,the timedependent derivative of the Hubble parameter is represented as

Now,we have an additional choice to pick one parameter because we have more unknown parameters with fewer equations to solve i.e.equations (18)–(20).The DE is typically described by an EoS parameter that is a ratio of spatially homogenous pressure to DE density.Recent cosmological investigations show that the ambiguities are too great to distinguish between the cases: ω<-1,ω=-1,and ω>-1[39–41].In the decelerating phase,which contains two epochs of matter and radiation,the EoS parameter takes the valuesand ω=0 respectively.The accelerating phase of the Cosmos,which has recently been explored,is represented withwhich contains the quintessenceΛCDM ω=-1,and phantom regime ω<-1.The value of the EoS parameter for DE estimated by Nine-Year Wilkinson Microwave Anisotropy Probe(WMAP9),which integrated data from H0measurements,SNe,CMB,and BAO,is ω=-1.084±0.063 [39],whereas the Planck collaboration shows ω=-1.006±0.0451 [40],and later in 2018,it published ω=-1.028±0.032 [41].So,the value of the EoS parameter flips from positive in the past to negative in the present.The parameterization of the EoS is a valuable way for reconstructing cosmological parameters and constraining the dynamical history of the Cosmos in ageneral scheme.There are numerous parameterizations for ωDEdescribed in the literature,see [42–45].In this work,we consider the SR parametrization form of EoS parameter for DE in terms of redshift z (ωQ=ωDE=ωSR) [46],

The parametrization employed in this study offers several key advantages in the context of modeling the EoS of DE.Firstly,it provides a physically interpretable framework,with ω0representing the DE EoS at the present epoch (z=0) and ω1characterizing the temporal evolution of DE.This transparency enhances our understanding of the underlying physical processes.Moreover,the parametrization explicitly incorporates the redshift dependence,allowing us to capture the evolving nature of DE over cosmic time.Its flexibility enables us to encompass a wide range of DE behaviors,from quintessence to phantom DE.This adaptability ensures that the parametrization can be fine-tuned to match a variety of observational data,making it a valuable tool for cosmological research.In addition,it clearly observes that the EoSparameter at high redshift (i.e.z →∞) becomes ωSR=ω0+ω1and thus depends on the values ω0and ω1.For z →-1,becomes asit behaves like DE throughout cosmic evolution and this is appropriate for ωDEin equation (20).

Using equations (20),(21),and (22),we obtain the following differential equation

Solving equation (23),we obtain the expression for the Hubble parameter in terms of z

where c0is a constant of integration.The current value of the Hubble parameter can be obtained as

Using equations(24)and(25),the Hubble parameter can be rewritten in terms of H0in the form

The deceleration parameter q is written as

In the current model,q evolves as a function of z as

The Om diagnostic is an important method for classifying the various DE cosmological scenarios[47].It is the simplest diagnosis since it just takes the first order derivative of the cosmic scale factor.It is expressed for a spatially flat Cosmos as

The negative slope of Om(z) leads to quintessence type behavior (ω>-1),whereas the positive slope,refers to phantom-type behavior (ω<-1).The constant nature of Om(z)represents the ΛCDM model(ω=-1).In the next section,we will attempt to estimate the ω0,ω1and n values using the Hubble and Pantheon data-sets.With the help of the ω0,ω1and n values,we discuss the behavior of the aforementioned cosmological parameters and verify the validity of the cosmological model.

4.Observational data

The several observational datasets may then be utilized to restrict the parameters H0,ω0,ω1and n.It is important to note that the EoS parameter ωDEfor DE (see equation (20)) is not dependent on the parameter α and hence is not explicitly contained in the Hubble parameter expression,i.e.equation(26),we attempt to fix it by setting α=1.We study the observational data using the standard Bayesian approach,and we get the posterior distributions of the parameters using the MCMC (Markov Chain Monte Carlo) method.In addition,for MCMC analysis,we use the emcee Python package[48].In this work,we use two data: Hubble dataset with 31 data points,and SNe dataset from Pantheon samples compilation dataset with 1048 data points.

4.1.Hubble dataset

We utilize a dataset consisting of 31 data points obtained through the cosmic chronometers (CC) technique.This approach allows us to directly extract information about the Hubble function at various redshifts,spanning up to z ≤2.The choice to incorporate CC data is primarily motivated by its reliance on measurements of age differences between two galaxies that evolved passively,originating simultaneously but separated by a small redshift interval.This method facilitates the calculation of Δz/Δt.Notably,CC data has demonstrated higher reliability in comparison to other methods that depend on absolute age determinations for galaxies,as previously discussed in[49].The CC data points utilized in our analysis were collected from references [50–56],all of which are independent of the Cepheid distance scale and specific cosmological models.It is important to acknowledge that these data points rely on the modeling of stellar ages,employing well-established techniques of stellar population synthesis (for further details,refer to [52,54,57–60] for analyses related to CC systematics).To evaluate the goodness of fit between our model and the dataset,we employ the χ2function,defined as

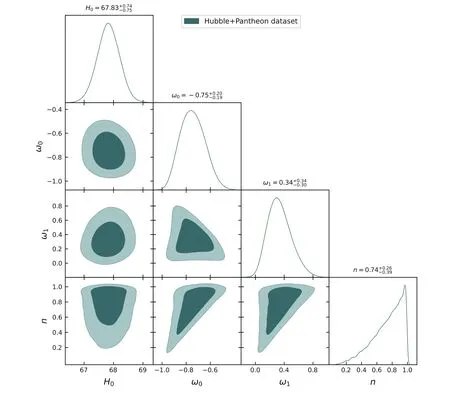
4.2.Pantheon dataset

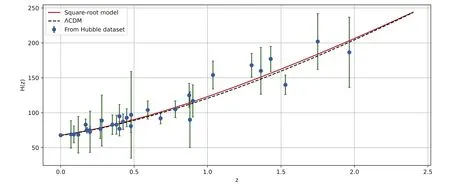
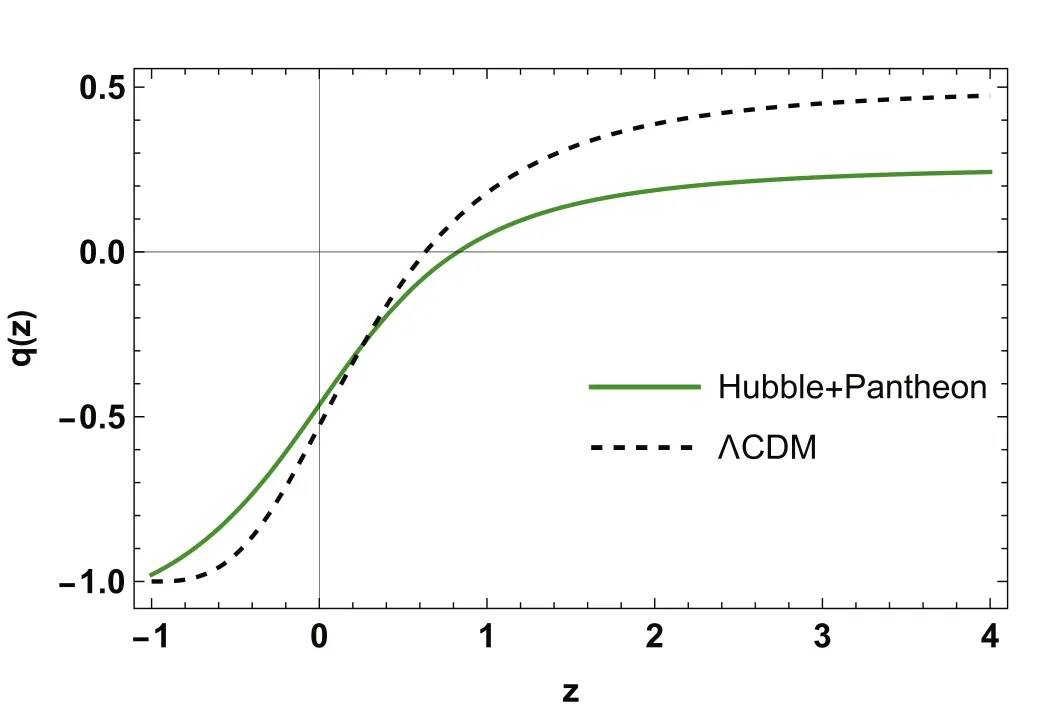
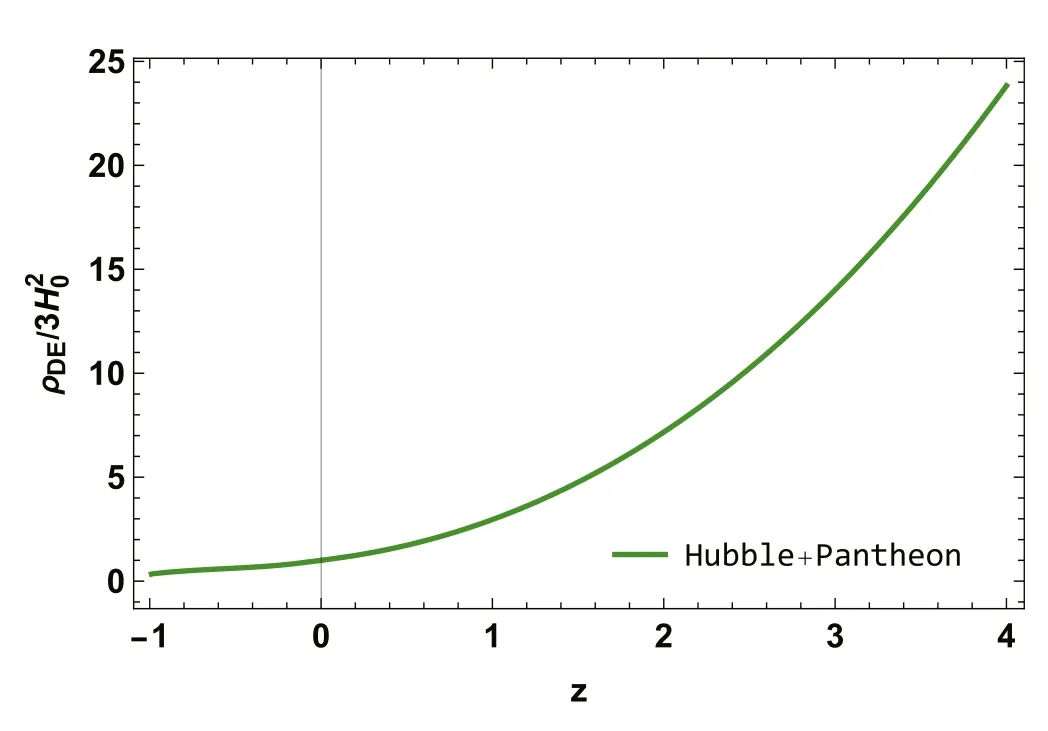
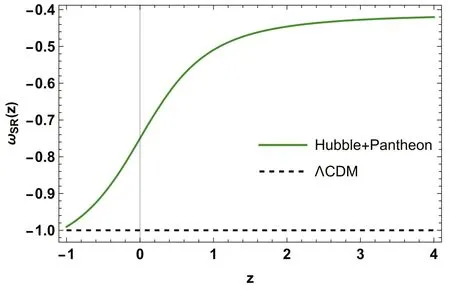
The SNe plays an important role in characterizing the expanding Cosmos.Moreover,spectroscopically acquired SNe data from studies that include the SuperNova Legacy Survey (SNLS),the Sloan Digital Sky Survey (SDSS),the Hubble space telescope (HST) survey,and the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS1) provide strong evidence in this path.The Pantheon dataset,the most recent SNe data sample,comprise 1048 magnitudes for the distance modulus evaluated over a redshift range of 0.01

4.3.Hubble+Pantheon dataset

In this section,we present the outcomes of the statistical MCMC method combined with the Bayesian analysis.We apply the joint analysis for the Hubble dataset with 31 data points,and the Pantheon dataset with 1048 sample points to constrain the parameters of the model H0,ω0,ω1and n from equation (26).We utilized 100 walkers and 1000 MCMC steps to get conclusions for the dataset.For the joint analysis,we consider the following priors:H0∊[6 0,80],ω0∊ [-2,2],ω1∊ [-2,2],andn∊ [-2,2].When only a dataset is used to estimate parameters,we presume a Gaussian likelihood.The quality of fit for the joint analysis is measured by a total chi-squared functionthat is defined as:

whereLTrepresents the product of the likelihood functions of each dataset.

Recent studies have highlighted the significance of Hubble parameter measurements and Pantheon data in constraining cosmological parameters.In our model,the parameters of interest are H0,ω0,ω1,and n.However,our primary aim is to assess the influence of parameters within the chosen parameter space and gauge their compatibility with observational data.Figure 1 displays the 1-σ and 2-σ likelihood contours derived from the joint analysis of the Hubble and Pantheon datasets.The best-fit values of the estimated model parameters areThe likelihood functions for the Hubble+Pantheon datasets are also extremely well matched to a Gaussian distribution function,as seen in figure 1.Figures 2 and 3 compare our RS parametrization model to the widely accepted ΛCDM model in cosmology,i.e.For the figure,we=0.314and H0=67.4 km.s-1.Mpc-1[41].The figures also include Hubble and Pantheon experimental findings,with 31 and 1048 data points with errors,respectively,allowing for a direct comparison between different models.

Figure 1.The confidence curves for the model parameters at 1-σ and 2-σ using the Hubble+Pantheon dataset.Dark green shaded zones indicate the 1-σ confidence level(CL),whereas light green shaded regions reflect the 2-σ CL.The parameter constraint values are also displayed at the 1-σ CL.

Figure 2.The variation of H(z)versus z.The blue dots represent error bars,the red line represents our model’s curve,and the black dashed line represents the ΛCDM model.

Figure 3.The variation of μ(z)versus z.The blue dots represent error bars,the red line represents our model’s curve,and the black dashed line represents the ΛCDM model.

Figure 4.The behavior of the deceleration parameter q versus redshift z.

Figure 5.The behavior of the density parameter for DE ρDE versus redshift z.

Figure 6.The behavior of the EoS parameter for DE ω versus redshift z.

Figure 7.The behavior of the Om(z) versus redshift z.

5.Cosmological parameters

Cosmological parameters play a vital role in the construction of cosmological models.For the model to be realistic,the current value of the deceleration parameter q must be matched with the cosmic measurements.Furthermore,the model’s decelerating or accelerating behavior is determined by the positive or negative value of q.The behavior of the deceleration parameter,energy density,and EoS parameter in terms of redshift is illustrated below.For the model parameter values,we use the Hubble+Pantheon data-sets.According to figure 4,the deceleration parameter clearly indicates the transition from a decelerated(i.e.q>0)to an accelerated(i.e.q<0) stage of the Cosmos expansion for the constrained values of the model parameters.The present value of the deceleration parameter(i.e.z=0)corresponding to the model parameter values constrained by the Hubble+Pantheon dataset isMoreover,the transition redshift(i.e.q=0) is[63,64] for the Hubble+Pantheon dataset.In addition,it is essential to point out that the q0and ztrvalues constrained in this paper are consistent with the value reported in[65–67].The behavior of the energy density of DE is shown in figure 5.As the Universe expands,the energy density of DE increases with redshift z,but decreases with time.At late times,the DE density reaches a minimum value.Moreover,the small value of DE density implies that the Universe will continue to accelerate in its expansion in the future,leading to the big rip scenario.

The EoS parameter is one of the cosmological parameters that are important in describing the status of the expansion of our Cosmos.So when the value of the EoS parameter is strictly less thanthe Cosmos accelerates.The behavior of the EoS parameter for DE is depicted in figure 6 based on constrained values of model parameters ω0,ω1and n from Hubble+Pantheon data-sets.It is seen that the EoS parameter for DE continues in the quintessence era,maintaining the Cosmos’s acceleration.The current value of EoS is calculated as[68,69].

In addition,the slope of the diagnostic parameter Om(z)can distinguish between two types of DE scenarios (quintessence and phantom).According to figure 7,theOm(z) for the constrained values of the model parameters has a negative slope over the whole domain.We may deduce from theOm(z)diagnostic test that our RS model depicts quintessencetype behavior.This indicates that our model exhibits unique characteristics when contrasted with the standard ΛCDM model.

6.Conclusion

DE is one of the most enticing and intriguing topics in current cosmology,as it contributes to the Cosmos’s accelerating expansion.Many attempts have been taken to explain this cosmic acceleration,including several parametrizations of DE models and modified theories of gravity.The goal of this research is to examine the SR parametrization model in the f(Q)theory of gravity as an alternative theory to GR,in which gravitational effects are attributed to the non-metricity scalar Q.We derived the exact solution of the field equations for the functional form of f(Q) as f(Q)=Q+αQn,where α and n are arbitrary constants,by using the SR parametrization form of the EoS parameter for DE aswhich leads to the variable deceleration parameter.To obtain the best-fit values for the model parameters ω0,ω1and n,we used the Hubble dataset with 31 data points and SNe dataset from the Pantheon samples compilation dataset with 1048 data points.The best-fit values of the estimated model parameters areandfor the Hubble+Pantheon dataset.In this case,ω0represents the current value of the EoS parameter for DE,which exhibits negative behavior and is situated in the quintessence epoch.In addition,we explored numerous cosmological parameters to assess the model’s feasibility.The deceleration parameter demonstrates that the Cosmos depicted by our model transitions smoothly from the early decelerated phase to the present accelerated phase.Further,the present value of the deceleration parameter corresponding to the model parameter values constrained by the Hubble+Pantheon dataset isThe transition redshiftfor the Hubble+Pantheon dataset.Finally,figure 7 shows that the slope of the Om(z) diagnostic parameter Om(z) is negative.Thus,the model presented here behaves like the Cosmos’s quintessence model.The f(Q)cosmological model under consideration can be viewed as a highly promising alternative to the ΛCDM model,and more research into its possibilities would be both intriguing and important.A similar examination will be carried out in a future publication.

Acknowledgments

This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (Grant No.IMSIU-RG23008).

ORCID iDs