Prompt photon production in proton–nucleus collisions at LHC: a comparison among color dipole models*

Hong-Min Wang ,Yan-Zhao Wang ,Yong-Han Xu and Xian-Jing Sun

1 Physics Department,Army Academy of Armored Forces,PLA,Beijing 100072,China

2 Department of Mathematics and Physics,Shijiazhuang Tiedao University,Shijiazhuang 050043,China

3 Hebei Key Laboratory of Physics and Energy Technology,North China Electric Power University,Baoding 071000,China

4 Institute of High Energy Physics,Chinese Academy of Sciences,Beijing 100049,China

Abstract The nuclear modification factor for prompt photon production in proton–nucleus collisions is investigated within color dipole formalism.By means of the Glauber–Gribov approach,the nuclear effects are studied in various rapidity bins with the evolution equation-based saturation models and the phenomenological dipole models.The theoretical results are compared with the experimental data provided by PHENIX,ATLAS and CMS Collaborations.At forward rapidity and midrapidity,a reasonable agreement with the experimental data is shown for the theoretical results with the modified Kharzeev,Levin and Nardi model,and the Kowalski and Teaney model.Then,we analyze the influence of the initial state energy loss effect on the nuclear modification factor and find that it is obvious only at backward rapidity together with small pT.Finally,the theoretical results are also compared with those of JETPHOX Monte Carlo program and the predictive results for the LHCb at very forward rapidities are presented.

Keywords: color dipole formalism,Glauber-Gribov approach,small-r limit

1.Introduction

The production of photons is an important tool for studying the properties of quark–gluon plasma (QGP) produced in heavy-ion collisions(HIC)[1].Among the photons produced in the HIC,prompt photons from cold processes are always considered as a background for thermal photons from the QGP.Furthermore,since photons are colorless,they are not sensitive to the final state interactions and can leave the QGP without energy loss.Thus,prompt photon production is an ideal probe to study the initial state of cold nuclear matter(CNM) effects.In 2013,the experimental data for prompt photon production in deuteron-gold (d+Au) collisions was extracted by PHENIX Collaboration[2].Recently,the data in proton-lead (p+Pb) collisions is also probed by the ATLAS Collaboration [3].These experimental data are used to study the CNM effects in prompt photon production.

The color dipole (CD) approach is an effective theory to describe both prompt photon and Drell-Yan dilepton production in proton-proton (p+p) collisions [4].In this approach,the prompt photon production is treated as a quark(or anti-quark) electromagnetic bremsstrahlung after exchanging a single gluon with the target [5].The phenomenology for the color dipole formulism is based on the q¯q color dipole cross-section,which incorporates the gluon radiation and nonlinear gluon recombination effects [6].The dipole cross section is always written as an integral of the forward scattering amplitude,which can be given by the CD models.The CD models can be divided into two kinds: the phenomenological models and the evolution equation-dependent models.The phenomenological CD models,such as the Golec–Biernat and W ü sthoff (GBW) model [7],the Iancu,Itakura and Munier (IIM) model [8],the Dumitru,Hayashigaki and Jalilian-Marian(DHJ)model[9]et al[10–13],incorporate the basic features of gluon saturation into the color dipole crosssection.Each of them has a different anomalous dimensionγeff,which is an important parameter in the CD model to determine the transition between the saturation regime and the DGLAP-like region (at large-pT).The evolution equation dependent saturation models,such as the Kowalski and Teaney (KT) model [14],the running coupling Balitsky-Kovchegov (rcBK) model [15],and the collinearly-improved Balitsky-Kovchegov (ciBK) model [16–18],are more successful in describing the data at small Bjorken-x and high energies than that of the phenomenological CD models.

In order to study the nuclear modification factor in p+A collisions,the nuclear effects should be considered.There are two methods to consider the nuclear effects in the CD framework.One simple way is via the geometric scaling (GS)property from the CD models.This method considers the nuclear effects by relating the saturation scale of the nucleus,Qs,A,to that of the proton,Qs,p,by multiplying a constant[19].In order to get more reliable theoretical results,we should consider the impact parameter (b) dependence of the nuclear saturation scale.With the standard Woods–Saxon nuclear density [20],the Glauber–Gribov approach can successfully consider the b-dependence effect [21,22].For a heavy target,the projectile partons will also undergo multiple scattering in a medium before the prompt photon production[23].This is called the initial energy loss effect.In recent years,it is still an ongoing subject on both experimental and theoretical sides [24–26].Therefore the initial energy loss effect is also considered.

This paper is organized as follows.In section 2,we present the theoretical framework.This section includes the prompt photon production mechanism,a review for the dipole-proton scattering amplitude in the color dipole models and how to consider the nuclear effects in the CD approach.In section 3,the theoretical results and discussion are given.The summary is given in section 4.

2.Theoretical framework

2.1.Prompt photon production in p+p collisions

In the color dipole formalism,the prompt photon production cross section in p+p collisions can be given by [4]

where y and pTare the rapidity and transverse momentum of the photon,respectively.is the proton structure function[27].α is the fraction of the quark momentum carried by the photon and the hard scale μ is taken asμ2=The prompt photon production cross section in the quark-nucleon interactions [28]

2.2.Dipole-proton scattering amplitude in the color dipole models

In order to investigate the nuclear effects entirely,we will consider the dipole-proton cross-section σdpwithin different CD models.In the eikonal approximation,σdpcan be given by [29]

where Ndp(x,r,b)is the dipole-proton scattering amplitude.If the b-dependence in Ndp(x,r,b) is neglected,the dipoleproton cross section can be rewritten as σdp(x,r)=σ0Ndp(x,r)withfitted to the experimental data.In the following,we review Ndp(x,r) given by the CD models.

The scattering amplitude in the GBW model [7] and the DHJ model [9] can be given by a more general form

In the IIM model,the scattering amplitude has a different form [8]

where β(≤1) is a parameter introduced at large Bjorken-x.The parameters are given by=0.6599,N0=0.3358,k=9.9 x0=0.00105 and λ=0.2063.

In the KT model,the dipole-proton scattering amplitude can be written as [14]

where αs(μ2) is the running coupling constant.The gluon density xg(x,μ2) can be given by the DGLAP evolution equations,and the proton shape function T(b)can be given by a Gaussian form

with BG=4.25 GeV-2.

In the rcBK approach,the dipole scattering amplitude can be written as [15]

whereKBal(rT,r1T,r2T)is the kernel for the running term,and the initial conditions of the dipole scattering amplitude is the GBW ansatz.

2.3.Nuclear effects in p+A collisions

For the phenomenological models,a very simple method to consider nuclear effects in p+A collisions is to obtain the saturation scale of the nucleus from that of a proton through a translation Qs,A=A1/3Qs,p[10].The nuclear effects are absorbed into the saturation scale of the nucleus.

The GS approach is another simple way to consider nuclear effects.In this method,the dipole-nucleus (dA)saturation scale can be written as [19]

where Rpand RAare the radii of the proton and nucleus,respectively.The parameter δ=0.79.Then the scattering amplitude for the nucleus can be obtained by

The above two methods can only give a rough estimate of the nuclear effects.The Glauber–Gribov method,which considers b-dependence,is an ideal tool to study nuclear effects.In this study,different from the method used in[31,32],we consider the nuclear effect by replacingrQ2s,p2 for the proton in equation (5) with [33]

for nucleus.Thus,the dipole-nucleus scattering amplitude can be given by

where A is the nucleon number.TA(bA) is the thickness function of the nucleus [20]

where ρ0is normalized constant with ∫d2bATA(bA)=1.d=0.54 fm and RA=1.12A(1/3)-0.86A-1/3fm.

For the DGLAP evolution equation-dependent KT model,the parton distributions in the nuclear environment are modified [34].Therefore the dipole-nucleus scattering amplitude should be written as

where the nuclear ratio Rgcan be given by the EPPS16 parametrization [35].For the rcBK approach,the nuclear effect can be considered by following [33].

The initial-state energy loss is another effect to suppress the prompt photon production cross-section in p+A collisions.The mean energy loss of an incoming parton in this study is simply taken as [36]

where 〈L〉A=3RA/4.ξ ≈2 GeV/fm can be extracted from the Drell–Yan data [25].The Bjorken scale x1can be correspondingly rewritten as

Considering the nuclear effects in p+A collisions,we introduce the nuclear modification factor

3.Results and discussion

For the effective anomalous dimension,γeffis an important parameter to study the nuclear modification factor,figure 1 showsγeffof different phenomenological CD models versus pTat different rapidity:y=-2(a),y=-1(b),y=1(c)and y=2(d).The curves are the results of the GBW model(solid curves),the M-KLN model (dashed curves),the DHJ model(dotted curves)and the IIM model (dash–dotted curves).It is shown thatγeffapproaches 1 for the DHJ model.For the IIM model,γeffis larger than 1 and has an abnormal value at forward rapidity,as shown in figure 1(d).This can also be seen in [29],where the saturation scale of the IIM model is different from other models.The γeffvalue for the M-KLN model is larger than 1 only at large pTat forward rapidity.

In equation(3),the modified Bessel function J0(J1)in the Hankel’s integral transforms is a high oscillation function.In figure 2,we give the results for J0and K0versus r.Figure 2(a)shows J0verse r at pT=100 GeV (solid curve) and 10 GeV(dashed curve).It is shown that the oscillation of J0becomes violent when pTis large.In contrast,as shown in figure 2(b),γ-production (solid curve) is very difficult to converge compared to the D-meson production (dashed curve) at the same α(=0.5) [29].Thus,it is very difficult to obtain accurate theoretical results for the Hankel’s integral transforms in prompt photon production at large pT.At large pT,the small-r limit can be applied for the dipole-proton scattering amplitude.In this domain,r ≈1/pTand the I1,2,3can be analytically given by [5].

Figure 2.The modified Bessel function J0 (a) and K0 (b) as a function of r.

The nuclear modification factor RdAufor the prompt photon production in d+Au collisions at200 GeV is shown in figure 3.Here,we neglect the nuclear modification for the parton distribution in deuteron.The experimental data come from PHENIX [2].Figure 3(a) shows the theoretical results for RdAuwith different color dipole models: the KT model (solid curve),the M-KLN model (dashed curve),the DHJ model(dotted curve),the IIM model(dash-dotted curve)and the GBW model (shot-dashed curve).As shown in figure 3(a),the nuclear effect (‘shadowing’) within the GBW model is not obvious.This is because the dipole-nucleus scattering amplitude in the GBW model can be approximately written asBy using the normalization of the thickness function of the nucleus,σdA≈Aσdpand the nuclear modification factor RdAu≈1.The theoretical result for the IIM model is unreasonable,especially at large pT.The reason lies in its abnormal γeff,as shown in figure 2.The results with the DHJ model and the M-KLN model fit the data well.These indicate that they are more reasonable in studying the nuclear effect for prompt photon production in p+A collisions.Although the result with the KT model is larger than that of the other models,it is still in the allowable error range of the experimental data.In figure 3(b),the influence of the initial energy loss effect is given with the KT model and the M-KLN model.The solid(dashed) curve is the result of the KT (M-KLN) model without energy loss,and the dotted (dash-dotted) curve is the result of the KT (M-KLN) model with energy loss.The PHENIX data in d+Au collisions are at mid-rapidity(|y|<0.35).As shown in [25],the gluon initial energy loss effect is more obvious than that of the quark.The prompt photon bremsstrahlung by quark (or antiquark),so the initial energy loss effect is not obvious in d+Au collisions at RHIC energies.

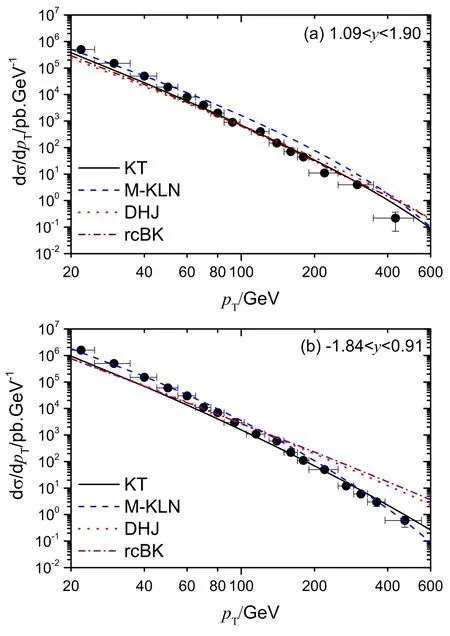
Figure 4.Prompt photon production differential cross sections in p+Pb collision at=8.16 TeV in different rapidity bins: (a)1.09

Figure 5.RpPb versus pT at=8.16 TeV.The figure captions are the same as those in figure 4.

Figure 6.Differential cross sections for photon production in p+p collisions at=13 TeV in different rapidity bins: (a) |y|<0.8,(b)0.8<|y|<1.44,(c) 1.57<|y|<2.1,(d) 2.1<|y|<2.5.

In figure 4,the results for prompt photon production in p+Pb collisions at forward rapidity(a)and midrapidity(b)are shown.The theoretical results are with the KT model (solid curves),the M-KLN model (dashed curves),the DHJ model(dotted curves)and the rcBK model(dash-dotted curves).The experimental data come from ATLAS Collaboration [3].The initial energy loss effect is neglected because it is too small to be considered at LHC energies[25].It is shown that the result of the KT model fits well with the experimental data at forward rapidity,where the Bjorken scale x2is very small.This demonstrates that the KT model is more effective at small x2.The results of the M-KLN model fit well with the data at forward and mid-rapidity.The results for the DHJ model are above the experimental data in the range pT>200 GeV at mid-rapidity.In this range,the effective anomalous dimensionγefffor the DHJ model approaches 1,as shown in figure 1,so the nuclear effect for the DHJ model disappears.The results of the rcBK model fit well with the experimental data at forward rapidity.However,its results are similar to those of the DHJ model at mid-rapidity.In conclusion,the theoretical results for the above models are all reasonable in fitting to the experimental data for prompt photon production when the Bjorken-x2is small.

The nuclear modification factorsfor prompt photon production are shown in figure 5.The figure captions are the same as those in figure 4.In order to compare with other methods,the theoretical results with the JETPHOX Monte Carlo program based on EPPS16 (shot-dashed curves) [37]and the IPSAT model including Reggeons (shot-dotted curves) are also given [31,32].It is shown that the nuclear effect for the rcBK method and the DHJ model are not clear.This is because the γefffor the DHJ model is close to 1 and the initial conditions for the rcBK method is the GBW model.As shown in figure 5(a),the results for the CD models are all reasonable at forward rapidity.At mid-rapidity when pT>200 GeV,the Bjorken scale x2∼0.01.For the effective range of the CD formalism is x2<0.01,x2∼0.01 is at the edge of the the CD model’s effective range.Therefore,the results for the CD models are slightly above the experimental data at mid-rapidity when pT>200 GeV as shown in figure 5(b).It is also shown in figure 5(b)that the results with the JETPHOX Monte Carlo program are above the experimental data at large pTtoo.Though the theoretical results with the IPSAT+REGGEON method are approximate to the experimental value when pT>200 GeV,its results are almost constant at forward rapidity as shown in figure 5(a).

In figure 6,the theoretical results for prompt photon production at13 TeV in p+p collisions are shown.The data come from CMS Collaboration [38].The solid curves and the dashed curves are the results with the KT model and the M-KLN model,respectively.It is shown that the theoretical results with the KT model fit well with experimental data at a large absolute value of y.For the M-KLN model,the theoretical results are larger than the experimental data.The reason is that the experimental data includes both forward and backward data.At backward rapidity,the Bjorken scale x2>0.01,which is out of the effective domain for the CD models.

In order to give a further study for the influence of the energy loss effect,figure 7(a) shows the results versus y at pT=2 GeV.The figure captions are the same as those in figure 3(b).It is shown that the initial energy loss effect is effective only at backward rapidity together with small pT.The reason is that the Bjorken scale x1(<0.00001) is very small at backward rapidity while pT=2 GeV.By equation (19),it can be obtained that the average change of the momentum fraction Δx1,which is also very small,is a constant at certain collision energies.Therefore,the influence of Δx1on quark distribution will become more obvious when the Bjorken scale x1is very small.This phenomenon can also be seen in figure 4 of[25].Figure 7(b)y=3,(c)y=4 and(d)y=5 show the predictive results for the LHCb in p+Pb collisions at8.16 TeV[39].The figure captions are the same as figure 4.An obvious deviation can be seen in the results between the KT model and the other two models.

Figure 7.Predictive results for the LHCb at =8.16 TeV.The influence of the energy loss effect versus y at pT=2 GeV is shown in figure 7(a).The predictive results versus pT at very forward rapidities are shown in figure 7(b) y=3,(c) y=4 and (d) y=5.

4.Conclusion

In summary,the nuclear modification factor for prompt photon production in p+A (or p+p) collisions is studied in the CD theoretical framework.By considering the nuclear effect with the Glauber–Gribov approach,the theoretical results are reasonable at forward rapidity for all of the color dipole models.This demonstrates that the CD formalism is an effective theory at small Bjorken-x.It is also demonstrated that a further study should be given for prompt photon production at mid-rapidity when pT>200 GeV.The predictive results for the LHCb at very large rapidities are to be verified by future experiments.