Universal resources for quantum computing

Dong-Sheng Wang

CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

Abstract Unravelling the source of quantum computing power has been a major goal in the field of quantum information science.In recent years,the quantum resource theory (QRT) has been established to characterize various quantum resources,yet their roles in quantum computing tasks still require investigation.The so-called universal quantum computing model (UQCM),e.g.the circuit model,has been the main framework to guide the design of quantum algorithms,creation of real quantum computers etc.In this work,we combine the study of UQCM together with QRT.We find,on one hand,using QRT can provide a resource-theoretic characterization of a UQCM,the relation among models and inspire new ones,and on the other hand,using UQCM offers a framework to apply resources,study relation among these resources and classify them.We develop the theory of universal resources in the setting of UQCM,and find a rich spectrum of UQCMs and the corresponding universal resources.Depending on a hierarchical structure of resource theories,we find models can be classified into families.In this work,we study three natural families of UQCMs in detail:the amplitude family,the quasi-probability family,and the Hamiltonian family.They include some well known models,like the measurement-based model and adiabatic model,and also inspire new models such as the contextual model that we introduce.Each family contains at least a triplet of models,and such a succinct structure of families of UQCMs offers a unifying picture to investigate resources and design models.It also provides a rigorous framework to resolve puzzles,such as the role of entanglement versus interference,and unravel resource-theoretic features of quantum algorithms.

Keywords: quantum resource,computing model,quantum algorithm

1.Introduction

1.1.Motivation

The attempt to identify the key resource for quantum speedup has ever been started at the birth of quantum computing.With notable discoveries such as the quantum teleportation [1],quantum entanglement was recognized to be a unique feature[2,3].At the meantime,from the study of early quantum algorithms[4,5]and the quantum circuit model(QCM)[6],it was proposed quantum interference is the source of power for quantum computing [7].A quantum algorithm is to make superposition of many computing paths,and then use interference to select the correct one quickly.

Along with the development of entanglement [8],it was proved that,surprisingly,entanglement is not sufficient for quantum speedup[9,10]in the setting of measurement-based quantum computing(MBQC)[11].This was later extended to the circuit model by showing that a small amount of entanglement is enough to achieve universality [12].This partly motivated people to investigate other resources,such as quantum contextuality [13,14].Indeed,it was claimed that quantum contextuality serves as the magic for quantum speedup [15] based on the model of magic-state injection[16],and this paradigm has been expanded from then on;e.g.[17–20].Recently a close relation between MBQC and SPT order [21–23] has been established [24–28],but a resource theory was not developed yet.

An important precursor for general quantum resource theory(QRT) [29] is the resource theory of quantum coherence [30].Measures of coherence have been studied from various perspectives [31–36],but only the resource-theoretic framework is complete.Quantum features can now be rigorously defined in the framework of QRT.Given a setS,a QRT over it is to identify a subset F⊂ S and the set of operationsO that preservesF,and then the rest ofS is treated as resources.A measure can then be defined to quantify the amount of resources and used to characterize the conversion between resources.

QRT does not provide methods of how to find the socalled free setF and free operationsO,however.In quantum computing,this can be especially full-filled by methods from universal quantum computing models (UQCM) and also algorithms.Namely,UQCM considers various settings: sets and operations on them,and an efficient algorithm can quickly realize an operation on the set,and these settings provide the places to define the free set and free operations.

In this work,we combine methods from QRT and UQCM and find fruitful results.We find QRT provides a way to define and classify UQCM,and identify the universal resources,and UQCM provides the place to define universal resources and classify them.From it,we can resolve puzzles such as the tension between entanglement and interference,the relation between coherence and contextuality,and we also find important new UQCM such as the model directly based on quantum contextuality,which is in the same family of magic-state injection.Below we survey some previous work and then summarize the main findings of this work.

1.2.Previous work

Due to the richness of the subject,there are many research lines that are relevant.Here we highlight a few points that are most relevant for the study in this work.

• In many study of QRT,a resource is not necessarily universal,i.e.not required to enable universal quantum computing.For instance,the QRT of thermodynamics defines athermality [29] which does not aim for computational universality.Here,our study of QRT is for UQCM.A UQCM is a framework to realize any quantum algorithms,and two models are equivalent if tasks or algorithms in them can simulate each other efficiently.The universality requires to consider different types of operational tasks instead of individual ones,as some tasks are special or interchangeable.Therefore,we introduce universal resources to characterize each UQCM.This provides a solid computational scheme to classify quantum resources.

• A classification for UQCM was developed [37].It proposed a table for UQCM with two categories based on a ‘quartet model’: with bipartite input structure and bipartite evolution structure.See figure 1 (left).One category is for fault-tolerance,i.e.coding-based models,and one is for universality.In this work,we only study the category for universality,and all the three families we identify belong to this category.Using QRT improves the quartet model: the bipartite input is specified to be free states and universal resources,and the evolution gates is specified to be free operations.Previously,MBQC and adiabatic quantum computing(AQC)[38]were treated as coding-based models since they can be viewed as dynamic coding methods.However,if we only restrict to static coding method,then MBQC and AQC must be treated using other methods.In this work,we find MBQC belongs to the amplitude family,and AQC belongs to the Hamiltonian family.Our classification in this paper is an improvement of the previous one.

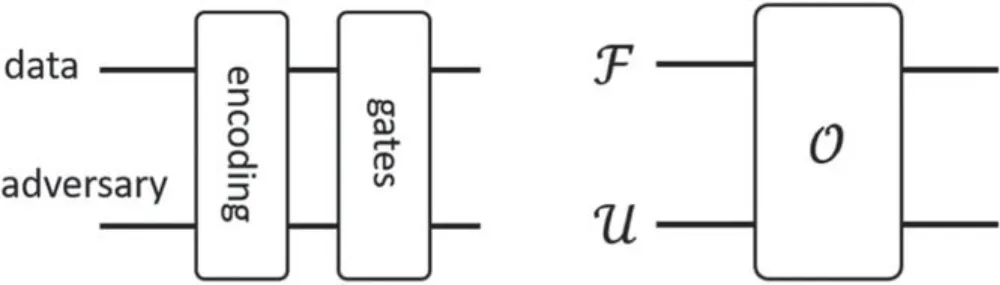
Figure 1.The ‘quartet model’ [37] (left) and resource-theoretic model (right) for universal quantum computing.

• Although in the past MBQC was not studied along with QRT,many studies on this subject are precursors for a resource theory of it.The universality for MBQC was largely explored before the rising of QRT [39,40],such as the measure of entanglement width.A classical version of MBQC was defined [41].As was mentioned,highly entangled states are mostly useless for this model[9,10].Instead,recently it was found that symmetryprotected topological(SPT)order is resourceful[26–28],and this lays the foundation for our resource theory of MBQC in this work.Quantum contextuality [13,14,42–44]has also been investigated for this model[45,46],but was not claimed to be the universal resource.In this work,we will further analyze the notion of quantum contextuality,and introduce a model directly based on it.

1.3.Summary

The basic model for our study is shown in figure 1 (right).It has two registers: the dataF and the resource U,and the computation are free operationsO.The initial states for data are free states,so it is clear that using resource U enables a computation by consuming it.In a resource theory,a free set F can be a set of quantum states.If this is not the case,we can convert it into a set of states by considering the effects on statesI.n quantum theory,we mainly study states,evolution,observable,and probability from measurement.Therefore,we can identify four families of UQCMs from each of them.More specifically,we consider the set of local Hamiltonian for the observable family.So we introduce the amplitude (or state) family,(quasi-)probability family,Hamiltonian family,and evolution family of UQCMs.The later one will be studied separately.Therefore,a family of UQCM is identified by the setS.A UQCM can be defined from a QRT,(F ,O,R).Then depending on a hierarchy of resource theories,i.e.a subset hierarchy of a few free sets,we can define the generations in a family of UQCM.Here we identify three generations for each family.We must be aware that such generations are neither unique nor complete due to the flexibility of the hierarchy of resource theory.

We now briefly describe the contents of the three families: denoted as the a,p,and h families.The a-family contains the QCM,local quantum Turing machine (LQTM)[47],and MBQC.In QCM,for quantum algorithmic speedup or primacy,we identify quantum interference as the resource.For LQTM,the ebit (or Bell state) is the universal resource,serving as quantum memory and enabling the representation of any states as matrix-product states (MPS) [48–50].In MBQC,a resource MPS is measured by a sequence of adaptive on-site projective measurements.We identify a special feature relating to SPT order as its universal resource.

The p-family contains the contextual quantum computing(CQC) that we introduce,magic-state injection (MSI),and post-magical quantum computing (PMQC) that is motivated by a nonlocal teleportation scheme[51].The MSI is powered by the so-called magic,often held by the |t〉=T|+〉 state.The magic is stronger than contextuality,though,which then allows a UQCM directly based on contextuality.It turns out this CQC model is interesting,and can explain features of some quantum algorithms,such as the linear combination of unitary operations [52,53].Using even stronger nonlocal boxes[51,54],the communication complexity can be brought down to minimal,enabling the PMQC model which is a variation of blind MBQC [55].

The h-family contains Hamiltonian quantum simulation(HQS) [56–59],Hamiltonian quantum cellular automata(HQCA) [60–62],and AQC [38].It relies on the set of local Hamiltonian interaction terms and how to manipulate them.The HQS allows almost any forms,HQCA allows the so-called parallel ones,and AQC only allows adiabatic changes of interaction terms It is then interesting to see that they indeed form a family and there is a hierarchy of interaction effects.

Physically,the a,p,and h families are distinct and their major physical characters can be understood from the perspective of quantum coherence,correlation,and interaction,respectively.There is indeed a hierarchy of resources for each of them.For states,this is from coherence to entanglement,and to a special multipartite entanglement.For probability,this is from local correlations of a few bits to nonlocal correlations.For Hamiltonian,this is also from local to nonlocal ones.A more powerful resource can be prepared from a less powerful one by proper operations defined from their free operations.A hierarchy is precisely characterized by a family of resource theories.

For clarity,the main findings are listed below:

• We extend resource theory to the setting of universal resources.This finds a place to use resource theory,and draw connections between quantum information and quantum computing.

• We use QRT to study UQCM and introduce families of UQCMs,which stands as a unique approach to unify and classify them,examine their physics,and find new ones.

• We define a universal resource theory for MBQC,and we clarify the relation with contextuality.

• We introduce the models of CQC and PMQC,as generations in the p-family.

• We present a primary resource-theoretic study for Hamiltonian-based models.

Table 1.The abbreviations of models and their full terms.

• We study the relation between quantum algorithms and resources.This helps to resolve puzzles,inspire ideas for new quantum algorithms.

Besides,we leave the study of the evolution family to the future,which is relatively less well studied.It may relate to superchannels [63],dynamical resource theory [29],and quantum von Neumann architecture [64].Also we believe there should be at least one coding-based family,which contains models based on error-correction codes [37].This would include topological quantum computing [65],multiparticle quantum walk [66],for instance.Also note that our classification of UQCMs does not aim to cover all known existing models.Instead,it provides a resource-theoretic framework to investigate and fertilize them.

This work contains the following parts.In section 2,we review QRT and then define the universal resources.We then introduce families of UQCMs.We study the details of each family in sections 3,4,and 5.We then analyze a few quantum algorithms in section 6.We conclude in section 7 with perspectives of future directions.For convenience,the various abbreviations for the models studied in this work are summarized in table 1.

2.Universal resource

2.1.Resource

We start from a brief review of QRT over a set of states.We consider finite-dimensional Hilbert spaces.For a quantum system with a Hilbert spaceH of pure states and the set of density operatorsD,a resource theory is defined by a tuple

with F⊂ D as the set of free states,O :F→Fthe set of free operations,and R ≔ D F the set of resource states[29].To quantify resources,we require the following axioms for a measure f:

(i) It is zero for free objects;f(ρ=0),∀ρ∊F;

(ii) It is positively upper bounded for finite dimensional Hilbert spaces;

(iii) It is asymptotically continuous;f(ρ)→f(σ) whenever ρ →σ,∀ρ,σ∊D;

(iv) It is subadditive;f(ρ ⊗σ)≤f(ρ)+f(σ),∀ρ,σ∊D;

(v) It is non-increasing under free operations;f(ρ)≥f(Φ(ρ)),∀φ ∊O.

The subadditivity condition (iv) can be strengthened to additivity for some measures of resources that we will use in this work.

There are a few generic approaches to quantify the amount of resource of a state,R(ρ),including distance-based measures,entropy,Fisher information,witness,and majorization [29].For instance,for a contractive distance d,a distance-based measure of resource is

This includes the trace distance of resource and fidelitybased measures.The relative Renyi entropies can also be used.For the widely usedS(ρ‖σ)=-tr [ρ(l ogσ-logρ)],the relative entropy of resource is

It was shown that there exists a free parameter estimation protocol for any resource stateρ∊R with an effective Fisher information being nonnagative [67].

In this work,we also consider QRT more abstractly.The setF does not need to be a set of states.Instead,it could be a set of Hermitian operators,unitary operators,quantum channels,or measurements,for instance.We can always use resource measures of states for these cases by considering operation effects on states.Also we do not employ resource conversions such as distillation as our focus will be on universal resources for quantum computing.

2.2.Universal resource

We now define the notion of universal resource,which,roughly speaking,is the resource that enables universal quantum computing.Formally,we define a universal resource theory as

with an additional set U⊂ R as the set of universal resource states,compared with a usual resource theory.The universality means thatO (F ⊗ U)simulates any quantum algorithms efficiently.See figure 1 (right).Here,efficiency means that the costs for the free operationsO,free statesF,and universal resources U all do not grow exponentially fast with the size of the given algorithm.

Actually,this formalism offers an unique way to define a UQCM.From computer science,there is an algorithmic approach:for a class of problems,a family of algorithms exist to solve them with a universal way to measure the complexity of each algorithm,e.g.circuit cost,oracle calls,or steps in Turing machines.Two models are equivalent if algorithms from them are polynomially equivalent.

From our QRT formalism,we need to findO andF.The F relates to how information is represented.This is important since it relates to how to measure the complexity of algorithms.With QRT,the cost ofO andF shall be counted separately from the cost of U,with the later being more important to measure the complexity of algorithms.This is an improvement of the quartet model we introduced before[37],figure 1 (left).The adversary now serves as the universal resource,and the data register is the free states.The gates are free operationsO,which can be logical,i.e.an encoding may be implicit.

A universal resource is the optimal resource defined in a resource theory in order to promptO to achieve universality.Its value is given by

This formula can be relaxed to be R(U)=maxρ∊RR(ρ)since most likely R(ρ)would be the same for allρ∊U.We see that a measure for a universal resource is not for states,instead,it is for a set.For instance,it can be a measure of distance between sets

In general,themin andmax functions do not commute,but for convex sets and convex measures,the von Neumann-Fan minimax theorem shall apply to make them commute.

Furthermore,it is viable to introduce a weaker notion,‘distilled universality,’ to capture resources that can be efficiently distilled to a universal resource.For instance,we find ebit is a universal resource,and those entangled states that can be used to distill ebits efficiently will be considered distillable universal resource.In most QRTs,it has been shown that[68],asymptotically,all resource states become reversible using operations that are resource non-generating for the set of free states.Resource conversion via distillation or other means is an important part of a QRT.In this work,we employ the universality that does not rely on resource distillation.

2.3.Families of models

By considering different types of sets and operations,we can define different UQCMs.For the sets of states,(quasi-)probabilities,and local Hamiltonian,we introduce a family of UQCMs for each of them.We use the term‘family’since for each of them there are also different UQCMs.In particular,for each family we identify a triplet of models,forming a hierarchy of universal resources.Namely,there is an order for their computing power of the universal resources.For two resource theories,ifF1⊂F2,thenO1⊂O2.When the total state space is fixed,R1⊃R2,i.e.more states are treated as resourceful in the first theory.However,to achieve universality,more resource power is needed for the first theory.We denote

which reads ‘the universal resource U1is computationally more powerful than the universal resource U2.’ Then the following conversions between the two universal resources are possible

for universal resource states∣u1,2〉 ∊U1,2,modular free states.

We now describe the conversion between universal resources for each family,with the establishment of QRT foreach model explained in the following sections.See the tables 2,3,4 for a brief summary.

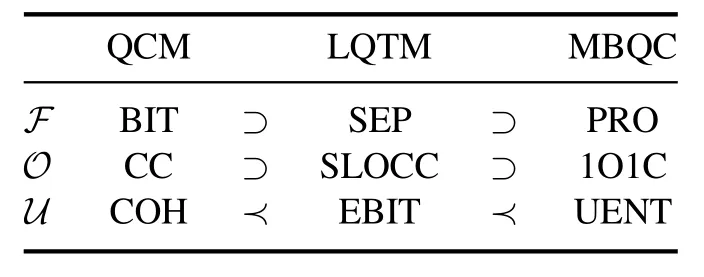
Table 2.The triplet of the amplitude family of UQCMs.Details can be found in section 3.

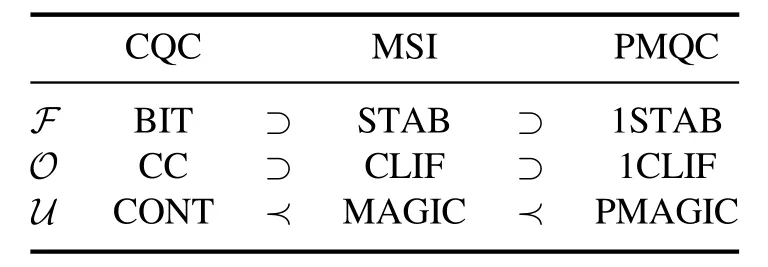
Table 3.The triplet of the probability family of UQCMs.Details can be found in section 4.

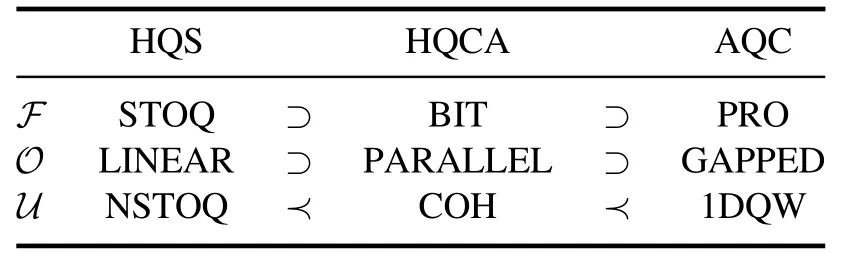
Table 4.The triplet of the Hamiltonian family of UQCMs.Details can be found in section 5.

The a-family relies on the set of states.Information is carried by the amplitudes ψiof pure states

expanded in an orthonormal basis {|i〉},and computation is the arithmetic of amplitudes,i.e.interference.A mixed state or density operator ρ can be viewed as a mixture of pure states ρ=Σαpα|ψα〉〈ψα| with a probability distribution pαover a set of pure states {|ψα〉}.

We find the QCM,LQTM,and MBQC form a triplet of generations in the a-family.Their universal resources are coherence (COH),ebits (EBIT),and special entanglement denoted as UENT.From a qudit ‘plus’ statewhich has maximal COH,an ebitcan be generated as

for the controlled-not gate CX,which is free in QCM but not in LQTM.With ebits,any state can be expressed as an MPS[48–50] form

forPnas local operators that are free in LQTM but not in MBQC.This includes the 2D cluster state [11] and AKLT state [48] that contains UENT as the universal resource.

The p-family relies on the set of probabilities or quasiprobabilities,relating to measurement effects.By expressing a state as

in a Hermitian operator basisit is characterized as a vectorFollowing Wootters[69],the vector satisfies sum=1 in a proper basis. If≥0, it can be viewed as a probability distribution, while in general there are negative values. So a state is treated as a quasiprobability,i.e.Wigner function,and a computation is the change of it.

The p-family is motivated by the MSI model[16].In this model, the free set is formed by stabilizer states (STAB), all with positive Wigner function [70], and Clifford operations(CLIF) are free. This selects out the magic state

as the universal resource,for T known as the T gate.However,not all states with positive Wigner function are stabilizer states[71].This implies that below MSI,there is a more basic model that directly captures the negativity of Wigner function.As Wigner negativity is equivalent to quantum contextuality [43],we introduce the model of CQC.In this model,we use the superposition of quantum contexts as universal resource,requiring states like |t〉,|+〉,and ebit |ω〉,and also measurement feedback (classical communication).

For both models,classical communication is required to deterministically realize a gate.This reveals the role of correlations.There is a stronger form of correlations,known as Popescu–Rohrlich (PR) nonlocal box [54].It is discovered that the PR box can substitute the classical communication for T gate teleportation [51].This motivates our definition of the PMQC model,which relates to MBQC and also instantaneous nonlocal quantum computation.Quantum teleportation is free in MSI but not in PMQC.

The h-family is based on the set of interactions,i.e.Hamiltonian terms.We consider local terms and the switching on and off of them as operations.An initial input state of an algorithm can be treated as an eigenstate of a Hamiltonian

and then use arithmetic of Hamiltonian to change H.We find HQS,HQCA,AQC form the triplet generations in the hfamily,with different free sets of arithmetic of interaction terms.

Although it dates back to the origin of quantum computing [72–75],we find the foundation of HQS is the notion of a universal set of H terms[56–58],just like a universal gate set.Given a setS,a Hamiltonian is constructed by a realweighted sum

for amplitudesjn∊R and each termhn∊S.The evolution U=eiHtwill be Trotterized with a sequence of local terms[73].It has been known that almost all two-local terms are universal,with stoquastic or classical ones as special forms [56–58].We define stoquastic Hamiltonian as the free set.

The HQCA model,as a class of QCA,relies on parallel switching on and off local terms Each step has a special jnand also tn.In other words,HQCA is a special HQS,just like the case with LQTM and QCM.It requires a special local term with larger locality for universality.The free set is the classical CA,which can be classically universal.Finally,the AQC uses adiabatic sum of local terms,with no gap-closing which protects the information encoded in the ground state manifold.The free set is product of local states,equivalent to on-site Hamiltonian,and the universal resource is equivalent to a 1D quantum walk derived from the Feynman–Kitaev circuit-to-Hamiltonian map [5].

3.The a-family

3.1.Quantum circuit model

In this section,we recall the quantum circuit model (QCM)and draw its connection with coherence and interference.For simplicity,we focus on the qubit case,and the extension to the qudit case is straightforward.It contains three basic stages:

(i) Initialize at the all-zero state |00…0〉 of qubits;

(ii) Apply a sequence of unitary gates;

(iii) Readout by measurements in the Pauli Z basis.

A quantum algorithm in the QCM is often described as a sequence of gates,possibly with additional classical pre and post processing.A central result is the existence of universal gate set from which any unitary evolution in the group SU(2n)can be efficiently constructed [6].Two well-known sets are{H,T,CX} and {H,CCX},for the Hadamard gate H and T gate as

and the controlled-not gate CX,Toffoli gate CCX,for τ ≡eiπ/8.The Toffoli gate itself is universal for classical computation,which motivates our resource theory for QCM.

We now introduce the QRT for QCM.The set of free statesF is the set of all classically efficiently representable states.The set of free operationsO is all efficient classical algorithms.That is,the free states and free operations form the usual classical computation that solves problems in the complexity class BPP (bounded-error probabilistic polynomial).We denote them as BIT and CC,for convenience(see table 2).The universal resource U will boost BPP to BQP(bounded-error quantum polynomial),enabling universal quantum computing and serving as the necessary and sufficient resource for quantum speedup.

The universal resource U contains the plus state

Figure 2.Quantum teleportation of H gate.

and any finite tensor-product |+〉⊗n,together with all their equivalents under free operations,such as the ‘minus’ stateThe plus state|+〉is the magic state for H gate since given |+〉,H can be realized by quantum teleportation,which are free operations.See figure 2.An intriguing fact is the measurement must be in the X basis,instead of Z basis.From a different perspective,we will show that this relates to the resource theory of contextuality studied in the next section.

It is clear that a classical circuit with Toffoli gates can only change basis states among themselves,while H can generate arithmetic on the amplitudes,which is interference.All gates that do not generate superposition are also classical,such as CX,phase gate S,and T gate.Free measurements not only contain Z-basis measurements,but also Pauli measurements.The classical measurement outcomes can be used as classical control over conditional classical gates,which also form free operations.

In QCM,a quantum circuit is usually not expressed with injection of plus states.Instead,it is often a sequence of unitary gates.In order to measure the power of quantum circuits,the QRT of coherence(COH)can be applied but it is defined for states.We introduce a new measure of interference (INT) power for gates,serving as the coherence measure of gates.

Given a state ρ,the ℓ1-norm measure of coherence is

It is not additive,though.It can be converted into an additive measure

and C(ρ)+1 is the ℓ1-norm of ρ.We call Q as the logarithmic coherence,or ‘log-coherence’ for short.It is clear that

It is maximum islogd,for d as the dimension,and this agrees with the maximum of the relative entropy of coherence

which is additive [76],for S as von Neumann entropy,Δ as the completely dephasing channel.With the eigenvaluespiof a state ρ,S(ρ)is the Shannon entropy H(pi)of the probability distributionpi.

To quantify interference,we need a dynamic measure of coherence.From channel-state duality[77,78],a processε is mapped to a Choi statefor the ebit ω=|ω〉〈ω|.Note we act the channel on the second part of the ebit for convenience.Then the coherence of this state can be treated as the interference power of the gate.However,this does not work.For instance,the Pauli gate X,Y,Z each is mapped to a Bell state which has nonzero coherence,yet we expect the interference power of Pauli gates is zero.This difficulty can be resolved by modifying the duality based on the following observation: the domain of such a measure is the free set,instead of the whole state space.We introduce a classical channel-state duality as follows.

Definition 1 Classical channel-state dualityFor a quantum channelε,its classical dual state is defined as

for projectorsPi=∣i〉 〈i∣,Δ as the completely dephasing channel.The dephased Bell state 1 ⊗Δ(ω) is maximally classically correlated.The coherence of the stateεmis

and the log-coherence is additive

and it is indeed additive.From the relative entropy and ℓ1-norm,the interference power of a gateε can be viewed as the average of the coherence of the output states ε (Pi)each created from a free statePi.We can now apply our measure to convince the intuition that Pauli gates have zero interference power,while Hadamard gate has maximal interference power on a qubit.We will apply this to study quantum algorithms in section 6.

3.2.Local quantum Turing machine

We now consider a computing model for which the free set of states is smaller than the set of classical states.The QRT of entanglement (ENT) is a natural fit.For the bipartite case,a state is separable if it can be written as

for bipartite partition A|B of the system.We also require that local dimensions are constants.The free operationO is stochastic local operation and classical communication(SLOCC),which can only preserve or decrease ENT.For a bipartite settingHd⊗Hd,statesare maximally entangled with ENT oflogd,including Bell states.

We find the computing model that relies on ENT as resources is the LQTM[47],as a simplification of the original ones [79–81].In this model,a computation requires two registers: one for the data,and the other as an adversary or‘machine.’ The machine interacts with each qubit in the data register one at a time,preparing a MPS

for a boundary operator B,whose role has been analyzed in details [47].The data qubits do not interact with each other directly,which is a natural locality constraint,and suggests ENT as the resource for LQTM.

Another way to represent MPS,actually the original one,is the VBS method[48].Note that the term MPS is often used for 1D systems with small ENT,while tensor-network states(TNS) or PEPS are for higher dimensions,but mathematically,they are all MPS [82].Given a collection of ebits,applying operatorsPnas SLOCC will prepare the MPS,see equation (11).This makes the role of ebits as universal resources U explicit.Non-maximally entangled states require distillation scheme [8],therefore are weaker than ebits.Without ebits,the SLOCC,as free operationsO,only generates separable states (SEP),as the free setF.

Although there are local coherence for separable states,they can be efficiently classically simulated,namely,by realizing the mixing and local states each with constant local dimension.The total Hilbert space dimension effectively does not grow exponentially with the system size.The local coherence under SLOCC cannot lead to ENT or large amount of INT.

The relation between ENT and COH has been well studied,e.g.[83,84].Given a bipartite settingHA⊗HBand the orthonormal product basis {|a,b〉},as the set of extreme incoherent states,the ENT of a state is upper bounded by its COH as

for U=UA⊗UBas a product unitary operators.This means we can study the ENT power of a gate based on the INT power of it.On the contrary,COH can also be quantified by ENT as

for daas the ancilla dimension,Λ as a bipartite incoherent operation [83].Using relative entropy,there exists a Λ (a generalized CNOT gate)that achieves the sup for da≥d.The ENT itself is also the COH of the final state.

Physically,ENT and COH are not the same.COH describes global feature of a system.ENT is a special COH,shared or distributed,and it identifies the quantum correlation among parts of a system.Such a quantum correlation can be understood as quantum memory.In a different study,the channel derived from MPS is termed as channel with memory[85].For LQTM,it is indeed intuitive to treat the control machine as ‘memory.’ In quantum communication,building up a remote ebit can send quantum information from one party to the other [1].Recently,it is shown that ebit is the basic element for quantum memory [64] relying on the channel-state duality.A stored quantum program is a Choi state built from ebits,the local measurements on which execute the read/write operations.

3.3.Measurement-based quantum computing

We now study a model that identifies special entangled states as universal resources,hence more restrictive free states and operations.For instance,the Bell-state measurement [6] will not be a free operation.This is MBQC,which often contains two parts:

(i) A universal resource state;

(ii) A sequence of on-site adaptive measurements.

A classical side-processing of measurement outcomes is required.The well-known original state is the 2D cluster state[11] and the underlying mechanism for gate execution is identified as gate teleportation [86].It was later extended to MPS by writing a resource state as

with the data|ℓ〉carried by edge space,and a sequence of onsite adaptive local projective measurement(LPM)on the bulk to induce universality on it [87].The LPM can also be extended to local POVM [88].Recently,this is also understood as a one-way code switching on edge codes[37].The switching can be made fault-tolerant by code concatenation and error correction.

Without the resource state,on-site adaptive measurements can only generate product states.So we identify the set of free statesF as product states(PRO),which is a subset of SEP.The free operationsO are 1-site operations (1O) and 1-way classical communication (1C),denoted as 1O1C.The 1O1C acting on PRO does not generate SEP,in particular,it does not generate globally shared pbits.This type of pbits shall be generated by 1O1C on the resource state.

Recently,the close connection between MBQC and SPT order is shown [26–28].SPT ground states are injective and have a well-defined locality.Namely,its local sites are defined such that the local tensor A is injective.The injectivity means that we can achieve any action on the edge space by acting on the physical spins [23,89].Often,translational invariance is present.An injective tensor may be obtained by blocking a few sites.This will violate the 1O1C condition.For MBQC,it further requires the more restrictive on-site injectivity,and this can be provided by SPT order.

At present,three classes of SPT order are known to be universal.This includes some 2D AKLT phase [88,90] with weak SPT order,2D cluster phase [28] with 1-form SPT order,and some hypergraph states [91,92] with strong SPT order.Meanwhile,it is known that some graph states are also universal,whose ENT is captured by the measure of entanglement width [40] and does not need to be SPT apparently.

Figure 3.A schematics for the information flow(the arrow)from the input(blue region)to the output(yellow region)of a computation in MBQC that is labelled by (G,[ω]).

It is not hard to show that an injective MPS (or TNS in higher D) can be driven to a SPT phase by free operations,although this driving is not unique.Given a state|ψ〉,identify regions for the input,output,and bulk,and the information flow direction.See figure 3 for an illustration.A pair

of a symmetry,normally specified by a group G,and SPT class labelled by an element[ω]in a group cohomology needs to be chosen,hence fixing its local tensor A.Each local tensor of|ψ〉can be modified by free local operations to the tensor A.In other words,an injective TNS can be viewed as a SPT state with disorder and lattice defects (e.g.a few sites might be missing).For instance,universal graph states and weighted graph states can be viewed as variations of the 2D cluster state.Furthermore,using the distillation-like technique[27],states in a SPT phase can be driven to its fixed point by LOCC.

Therefore,we identify fixed points of 2D SPT order as universal resources.More precisely,any fixed point of 2D SPT order that is equivalent to the 2D cluster state under the 1O1C free operations.The notion of SPT ENT has been studied[93]for 1D abelian cases,and can also be extended to higher dimensions.The entanglement width [40] shows that the ENT of universal resources shall scale linearly with the logical system size.Therefore,we use the term universal-ENT(UENT) to identify the ENT in a universal resource for MBQC.

For resource conversion,it is easy to see from the MPS form,the 2D cluster state(and its equivalents),is prepared by applying LOCC that is not 1O1C on ebits.The local operations(11) in MPS are precisely of this nature.

It has been proven that random states with large ENT is not useful for MBQC [9,10].Indeed,the highly entangled states under MBQC mostly behaves like local pbits.So there is no globally shared pbits.This means universality requires some global features of the resource states,and this relates to symmetry which is indeed a global feature of quantum systems.For universality,we need both extensive ENT and onsite injectivity,the former is provided by the gapped feature of 2D systems,and the later is provided by the feature of SPT order.We shall also note that this does not mean highly entangled random states are useless in some other models.

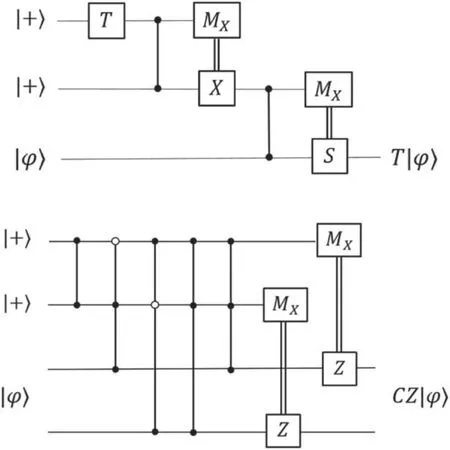
Figure 4.Quantum circuits to realized the T gate(top panel)and CZ gate (bottom panel).

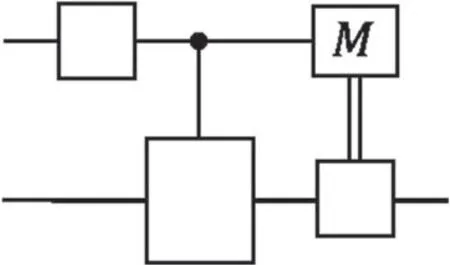
Figure 5.A schematics of the contextual quantum circuit in definition 2 with a control (top) and data (bottom) register.

4.The p-family

4.1.Contextual quantum computing

In this section,we introduce the model of contextual quantum computing(CQC).We start from the physics of contextuality,which has an origin from the hidden variable theories[13].A quantum context is a quantum operation,e.g.state preparation,evolution,or measurement [42].When two operations commute,then they are compatible,so can exist simultaneously.A compatible setting does not have contextuality,meaning that operators can be reduced to numbers.Quantum contextuality refers to the simultaneous existence of incompatible quantum contexts.Classical contextuality can be defined as the mixture of incompatible quantum contexts.We then characterize quantum contextuality (CONT) as superposition of quantum contexts.This motivates the model of CQC.

By expressing in the Pauli basis,we find the circuits for T and CZ in figure 4,also see the figure 2 for H gate.If Pauli operators are treated as primary quantum contexts,then each gate shows quantum CONT.These contextual circuits are universal since H,T,CZ form a universal gate set.

We now introduce a general definition of contextual quantum circuit,with an illustration in figure 5.

Definition 2 Contextual quantum circuitA contextual quantum circuit contains two registers: one as control,one as data,and it realizes process of the form

with a sandwiched structure: a special initial control state prepared by U1,a special measurement on the control prepared by U2with feedback to the data register,realized by CV and the trace over control,and the quantum-controlled gates CU in the middle with the data as the target.The two controlled gates,also known as multiplexer,take the form

for projectorsPi=∣i〉 〈i∣on the control,and unitary Uion the data.It realizes a gate U deterministically by expressing it as a linear combination of gates.The quantum control register is necessary since without it,a directly applied gate only leads to superposition of states.A mixing of contexts is realized by classical control.

Our definition can be slightly extended by using more general gates in the middle,which would contain feedback action on the control.We would not pursue this in details here.

In this model,measurements are important.Quantum measurement is described by POVM.A POVM is a set {Ei}for effects Ei≥0 and ΣiEi=1.A measurement on a state ρ yields three pieces of information: the outcome i,the probability of outcomespi=tr(Eiρ),and the final state ρifor each i.It is selective if the index i is explicitly known,and non-destructive if ρiis available.If it is a mixture,then it is effectively a quantum channel.

The classical outcome i is crucial to introduce in measurement-controlled operations: depending on i,different operators can be further applied.This is crucial for quantum teleportation and also for MBQC: the Pauli byproduct correction needs to be conditioned on previous measurement outcomes.Actually,contextual circuits can be seen as extensions of quantum teleportation.

We can now define the QRT of CQC.The free set is for BIT and CC,just like QCM,with the input for an algorithm as bits or pbits,computation circuit formed with S,T,CX,CZ,CCX,and any diagonal gates,but readout measurement only in the Z basis,and also Z-measurement controlled circuits.Such circuits can never generate superposition of states.

It is not hard to see the universal resource is the Pauli measurement MX.The selective MXnot only prepares the initial resource state |+〉,but also lead to the CONT.With free CZ and T gates,it also generates |ω〉 and |t〉.

Therefore,in our framework CONT is equivalent to INT.For QCM,we treat |+〉 as the resource but MXas a free operation.However,strictly speaking,MXcan prepare |+〉and is more suitable to be viewed as the resource-equivalence of Hadamard gate.We can use COH and INT directly as the measures for CONT of states and gates.For instance,the CONT of |t〉=T|+〉 is 1,the value of COH of |+〉.We will study the relation between CONT and INT more in section 6.

Although it is far from complete,the study above lays the foundation of CQC,At this point,it is interesting to draw the connections with other models.First,compared with QCM,the role of quantum control is explicit in CQC.A generic contextual circuit can have many control registers.A potential application is the setting of modular computing where control of unknown operations,as black boxes or oracles,is needed[94–97].An example is Kitaev’s quantum phase estimation(QPE)algorithm[5],which can estimate the phase factor θ for an unknown U but known eigenstate |ψ〉 of it,with U|ψ〉=eiθ|ψ〉.

The idea of interference of operators was studied in the model of duality QC [53,98],leading to the algorithm of linear combination of unitaries(LCU).LCU has been used in Hamiltonian-evolution simulation and others,which in general requires post-selection on the control register[52,99,100],making it probabilistic.This can be avoided for special cases of LCU,followed with measurement-controlled operations.To simulate a gate U in CQC,it first can be decomposed as a sequence of H,T,CZ,and then each of them can be deterministically realized by a contextual circuit.

Finally,CONT in MBQC has been studied [45,46],since measurement plays a crucial role.From the teleportation picture of MBQC [26],a gate is simulated by gate teleportation.We can treat the ancilla plus |+〉 or ebit |ω〉 state and MXas the resource for teleportation.The MBQC with the 2D cluster state is universal and must be contextual,and it requires measurements away from the Z basis.However,the teleportation picture will break a MBQC process into pieces,losing the global feature of it.Instead,we find our QRT of MBQC in section 3.3 is more natural for UENT,which is first given as a universal resource,and then consumed by free onsite local adaptive POVM.On the contrary,in CQC the role of contexts is explicit,and there is no need to prepare a highly entangled state at first.

4.2.Magic-state injection

The resource theory for MSI has been well developed [101].Here we briefly describe it for completeness.This model is suitable for fault-tolerant quantum computing with stabilizer codes,which usually allow transversal Clifford logical gates.In this model,the free setF is formed by stabilizer states(STAB) [102],all with positive Wigner functions [70],and Clifford operations (CLIF) are freeO.This selects out the magic state|t〉=T|+〉as the universal resource,for T known as the T gate.

A seminal additive measure is known as the ‘mana’[101].With the standard Wigner function Wρfor odd dimensional qudit states [69,70],the mana is

for the sum negativityN(ρ)=for Wρ(u)<0.To draw the connection with COH,it is clear that N(ρ)≤C(ρ),as the former measures the distance from STAB,while the later measures the distance from an incoherent set,as a subset of STAB[103].This is similar with the fact that ENT is smaller than COH for a state [83].

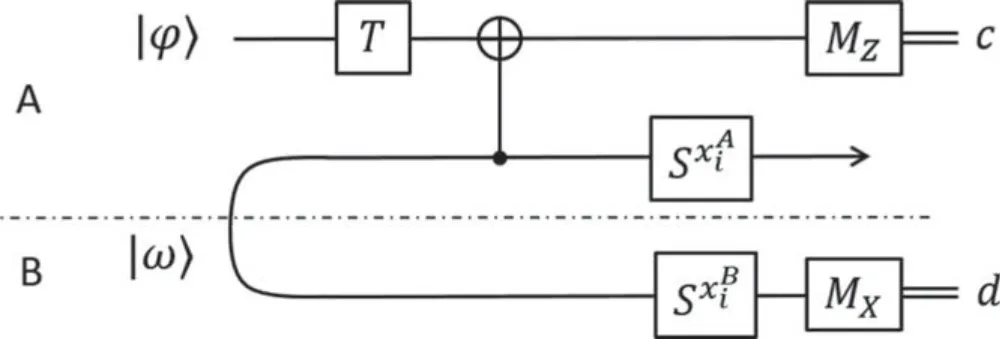
Figure 6.Broadbent’s non-signaling T gate teleportation.The curve is the ebit |ω〉.The middle wire with arrow carries the output.

4.3.Post-magical quantum computing

What would be a UQCM for which the universal resource is more powerful than MAGIC?We need to identify a subset of STAB.However,this is not unique.Here we study a model that relies on a stronger form of CONT than MAGIC,which is a type of instantaneous nonlocal QC (INQC),and has a close connection with MBQC.

We have seen that measurement feedback is useful.On the contrary,there are settings which do not allow or have serious limitations on this.An extreme example is INQC,which,instead of classical communication,only allows the broadcast of local results.Such class of operations has been termed as LOBC [104],as a subset of LOCC.A primary setting is a two-party nonlocal task: A and B each gets an input x,y,and then use LOBC operations to output a,b,which are then used to compute the result f(x,y).Security is a natural requirement,and here we consider the so-called onesided security [105],wherein one party can know the computation result.

A seminal scheme for encryption is to use Pauli operators XaZbfor encoding,with a,b ∊{0,1} as the keys [106].It is discovered by Broadbent[51]that the measurement feedback for T gate teleportation can be replaced by the Popescu–Rohrlich (PR) box [54],which on input x,y will output a,b satisfying

and this achieves the maximal violation of CHSH inequality[107],larger than the quantum value.Broadbent’s nonlocal T gate teleportation(BTT),shown in figure 6,forms the starting point of our PMQC model.In the usual T gate teleportation,a phase gate S needs to be corrected due to

This also means a T gate will destroy the update rule of the key.The phase gate is avoided by using an ebit and a PR box.The PR box is used to linearizeand the ebit is used to inject the valuesat a later time to cancel the S gate.

We now introduce the PMQC model.It is better described as an extension of the MBQC with the 2D cluster state.Instead of the usual cluster state,now each qubit has a ‘tail’(or partner),as in the figure 7,and a tailed cluster state

Figure 7.A schematics of a tailed cluster state |Φ〉 (38) on the 2D square lattice.

is prepared as follows.Identify all ‘heads’ (‘tails’) of the collection of ebits as party A(B).Given the ebitsas the initial state,a CZegate is applied between the nearest neighbor of party A for each edge e of the square lattice.Such a circuit is an example of tailed quantum circuits [64].

The universality of the 2D cluster state is shown by its ability to simulate the CZ gate and any qubit rotations,identifying each row as a logical evolution direction of a qubit.Instead of arbitrary qubit rotations,we only require H and T gates,which is universal for SU(2) [6].The H gate is realized by MX(a),leading to HZa,while T gate is realized by MX(b)TMX(a),leading to HZbHZaT=XbZaT.To implement a sequence of H and T on encrypted state in the PMQC model,see the top row of the cluster,the input encrypted state XaZb|ψ〉 is injected by measuring the leftmost tail site.The Pauli byproduct in a sequence like HXaZbTHXcZdHT…is brought out to the end via the BTT (figure 6).Namely,for each site in party A,an ebit and PR box are consumed.A CZ gate is realized as in the original MBQC.Therefore,we show that the PMQC model can realize the universal gate set{H,T,CZ } on encrypted data,provided by a client party B to a server party A who does not know the input and output of the data,with only a final round of broadcast communication between A and B.

To formulate a QRT of PMQC,first notice that all the T gates can be applied first before the measurements.Namely,in order to simulate a circuit of H,T,CZ gates,each simulated gate can be ‘imprinted’ to a site or edge of the sub lattice A,and T gates,which commute with CZ gates,can be applied on proper A sites leading to a circuit-specific cluster.Then only Pauli-basis measurements are required to simulate the circuit.So we identify tensor-product of single-qubit Clifford operations,and broadcast communication,as the free operation setO,denoted as 1CLIF.The free state setF,1STAB,contains tensor-product of Pauli eigenstates as extreme points.They are smaller than the free setting for MBQC,and also MSI.This selects out the circuit-specific tailed cluster states,and PR box together as the universal resource,with the PR box playing the central role.At present,we coin the term‘post-magic’ (PMAGIC) as the universal resource in the PMQC model.

The PR box was motivated by the study of quantum nonlocality (NONL),which now is often treated as a special type of CONT [44].Different from a generic setting of CONT,NONL does not allow conditional operations and nonlocal operations.It has been proposed to use LOSR (preshared randomness) as the free operations defining NONL[108].With local states as filters,it shows that ENT is equivalent to NONL.At this point,it could be enlightening to compare NONL with MAGIC.We established ENT,therefore probably NONL,as the resource for LQTM,sitting in between QCM and MBQC.Magic is the resource for MSI,sitting in between CQC and PMQC.NONL is not comparable to MAGIC,since MAGIC relies on conditional operations but NONL does not.MAGIC also depends on the Clifford hierarchy[109].We see that PMQC is a combination of MAGIC and NONL.

It is quite surprising the PR box is needed to achieve universality since its correlation is beyond quantum theory.Also the PR box does not need to be perfect: a slight postquantum correlation renders communication complexity trivial [110].It achieves a temperally ‘flat’ universal and blind MBQC [55].If the PR box is replaced by ebit,then an exponential amount of ebit is required to realize teleportation without communication [111].However,the allowed amount of classical communication could also be finite instead of being minimal.It remains to see if there is a quantum universal resource that is stronger than MAGIC,but weaker than PMAGIC.

5.The h-family

5.1.Hamiltonian quantum simulation

In this section,we study a primary model based on Hamiltonian evolution.In particular,we rely on the theory of a universal setS of Hamiltonian interaction terms[56–59],just like a universal gate set.First,aH′ simulate H,up to local encodingε,below energy Δ if

forH′≤Δas the restriction ofH′ up to energy Δ.More precise definitions can be found [56–58].The simulation cost is a function of the system size and interaction energy of H.Given∊,the time evolution U=eiHtis simulated with errors up to ∊t.

A HQS process is formed by a sequence of local evolutionwith local terms hn,parameters for interaction strength jnand time tn.It can be viewed as a Lie-Trotter sequence.Each local term can be drawn from a setS,and a simulated Hamiltonian is constructed by a real-weighted sum

for amplitudesjn∊R and each termhn∊S.

It has been proven recently there are universal Hamiltonian sets[56–59],such as the 2-local the Heisenberg and XY exchange interactions.Given a target H,the simulation scheme first maps it to a QPE circuit U [59],and then uses Feynman–Kitaev circuit-to-Hamiltonian map to obtain a Hamiltonian HFK[5],which is then simulated by a S-HamiltonianH′ relying on the perturbation gadgets [112].It does not directly simulate H in order to ensure the efficiency of the simulation,e.g.interaction amplitudes only grows polynomial with the system size.

A special class of Hamiltonian is known to be stoquastic,which has all off-diagonal elements being real and nonpositive.It is established that stoquastic Hamiltonian is more powerful than classical computation [112,113].This motivates our formulation of a QRT for HQS.The free setF is the set of stoquastic Hamiltonian,denoted as STOQ,and free operationsO are any linear combination that preserves the stoquastic-ness,denoted as LINEAR.For instance,the twoqubit stoquastic interaction is of the form αZZ+A1+1B forα∊R in a proper basis[112,113],while classical interaction is diagonal [114].A measure of the non-stoquastic-ness can be defined,e.g.by distance or entropy based measures,or by converting to the effects on states.However,we would not explore this in this work,and only refer to the particular form of the universal resources.

It is also valuable to draw the connection with and difference from other studies.The subject of quantum simulation of Hamiltonian evolution aims to simulate a given evolution U=eiHt(or time-dependent ones) in the QCM by decomposing it into a sequence of local unitary terms,e.g.using Lie-Trotter formula,but without referring to a universal Hamiltonian set [73,115].HQS can be viewed as an extension of analog(dedicated special-purpose)quantum simulation[116],which has a weaker requirement on the controllability of local terms.For instance,an analog simulator may have special form of local interaction terms,the local switching on and off of which may not be available.On the contrary,a HQS evolution is of digital natural since the set of hnis finite and the time parameter can be digitalized,i.e.broken into controllable segments.The requirement on time-dependence and classical control also makes it different from some Hamiltonian-based autonomous QC models [66,117–122],such as continuous-time quantum walk [66].This reveals that the primary feature of the h family is to explore the interactions among subsystems as resources.Whether other requirements such as automation can lead to other family of models is left for further investigation.

5.2.Hamiltonian quantum cellular automata

When the arithmetic on Hamiltonian terms is restricted,new models arise.In this section,we define a HQCA model which is a Hamiltonian-based QCA.

For classical computatoin,CA is a universal model.It is known that there are 2D universal CA,while 1D CA cannot be universal [45,123].It arranges bits on a lattice with welldefined neighborhood,and evolution is specified by parallel local dynamics;e.g.the value of each bit at a later time is determined by its neighbors at present.CA can be simulated by classical circuit.The local rule is mapped to a permutation P.But before it,we need a COPY step for each bit.The simulation circuit is of brickwork form,see figure 8,with a layer of COPY and a layer of P,and so on.

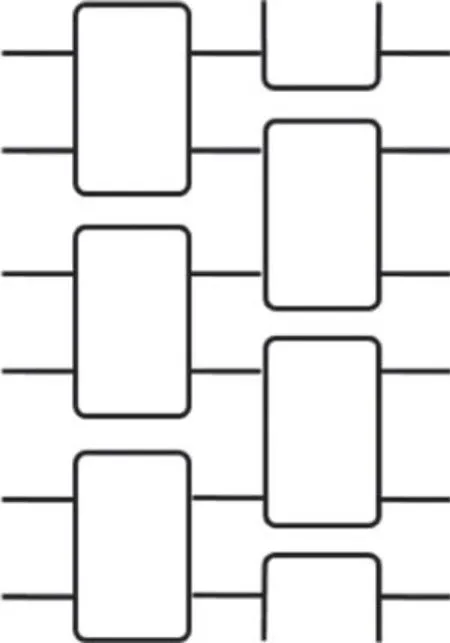
Figure 8.The schematics for a QCA brickwork circuit.

Diverse models of QCA have been developed [60–62].There are circuit-based and Hamiltonian-based ones,and here we use the later.Different from the classical case,1D HQCA can be universal,with two-local qudit intereaction terms We first sketch a seminal model to show how it works,and then introduce our model as a variation of it.In the Nagaj–Wocjan model[124],a local site with d=10 contains a few bands:for data qubit,program,and controller.The 1D chain is divided into many regions,with each region for a step in the simulated circuit.All the data qubits are located in a particular region.A translational invariant interaction is designed to simulate the circuit.Given a circuit of N qubits and M steps,the HQCA system size is MN and runs for a polynomial time.Intuitively,the model works like a typing machine: data qubits do not move,while programs are executed by shifting the states of the programs passing the data.The model is autonomous,and as such the desired final state |ψf〉 is only realized with finite probability under the evolution eiHt.The success probability can be boosted by repeating the algorithm or by modifying the model itself.

As for the HQS model,we allow classical control.Here we define a classically controlled HQCA,borrowing idea from the classically controlled QCA [125],which often composes a sequence of different QCAs,with each one controlled classically,i.e.switched on and off.Our model is defined as follows.For a 1D array of data qubits,add one ancilla qubit and program qutrit between each pair of data qubits.The bold local dimension is twelve,see figure 9.The local interaction is

with the first part as the ancilla qubit,and

with the first part as the program qutrit,for

with the first part as a data qubit,Π as the SWAP gate on two data qubits.The gate W is known to be universal if it can be applied to any pair of qubits [125].Note in HZ it is a Hadamard gate H.

Now given a circuit,composed with nearest-neighbor W and SWAP gates,first arrange it into a sequence of transversal steps.Each step then is a tensor product of W and SWAP gates.The program qutrit |p〉 encodes the type of gate,G ∊{1,W,Π},acting on two data qubits.The ancilla qubit is initialized to |1〉.A local evolution acts as

which does not alter the program qutrit but flips the ancilla qubit.The program qutrit and ancilla qubit needs to be reset before the next step.The timeis a constant so can be viewed as a fast quench,and the whole HQCA is treated as Trotterized steps forming a brickwork structure.

Observe that if the U (42) above is used instead of H(41),then the ancilla qubit is not needed.This basically reduces to a classically controlled QCA model [125].If the program qutrit values are dragged out,this will further reduce to the original circuit itself.On the contrary,the main feature of the HQCA model is the parallelism.One only needs to ensure the translational invariance of interaction.Also,compared with the autonomous ones [124,126],the use of classical control can ensure the deterministic preparation of the desired final state.

For a QRT of the HQCA model,it is natural to consider CA as the free setF.The free operationO is parallel control of local interactions,denoted as PARALLEL.However,the gate W does not reduce to the classical case apparently.With the similar idea,we can pick the gate set of Toffoli and Hadamard gates,and consider controlled-Toffoli and controlled-Hadamard gates as transversal steps,although this will enlarge the locality of interaction and local dimension.As Toffoli is universal classically,it is clear that the quantum resource is due to Hadamard gate,i.e.it is coherence.Therefore,we identify COH as the universal resource for this model.The relation between COH and NSTOQ can be seen by observing that the local four-body term H(41)is obviously non-stoquastic.The term H can be simulated in HQS by a weighted sum of two-body terms from a universal Hamiltonian set.

5.3.Adiabatic quantum computing

In this section we describe the AQC model [38].As it has been well known,we will merely show how it belongs to the h-family.In this model,usually one starts from the ground state|ψ0〉of an easy-to-prepare H0as the initial state,and then use adiabatic path

for the time-parameter t and the ground state |ψ1〉 of H1encodes the final output.The adiabatic condition requires the absence of gap-closing during the evolution,which drives |ψ0〉 through the ground manifold |ψt〉.We can also attach a sequence of adiabatic paths together,in general.

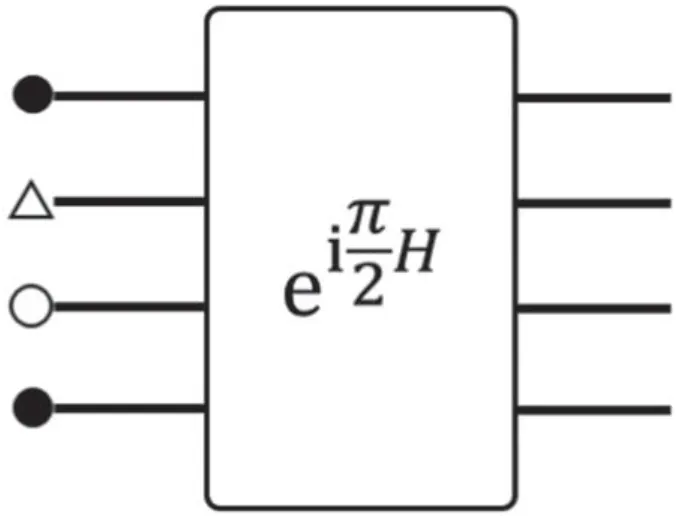
Figure 9.A local term in the HQCA model.The back dots are for data qubits,circle for an ancilla qubit,triangle for a program qutrit.

The standard method to prove the universality of AQC is the Feynman–Kitaev history-state method.Given a circuit U=U1U2…UL,it is mapped to a five-local,but not geometrically,Hamiltonian HFKwhose ground state is the history state

for |γℓ〉=|ψℓ〉|ℓ〉,andas the initial data state,and|ℓ〉as the state of a clock register.An adiabatic path H(t) is then design with |γ0〉 as the ground state of H(0),and|Φ〉as the ground state of H(1).The history state only yields the output with probability 1/(L+1).This is amplified by padding the circuit with a sequence of identity gates,using more clock qubits and interaction terms,so that the success probability gets close to 1.

We now define the QRT for AQC belonging to the hfamily.We use on-site terms as free setF,corresponding to free product states,PRO,which are often set as the initial state |ψ0〉 of an algorithm.The free operationO,denoted as GAPPED,is the adiabatic turning on and off of on-site terms,which is required not to induce gap-closing for each on-site term.Indeed the adiabatic on-site switching is a special type of parallel or transversal switching.Then the universal resource is the terms that can lead to universal QC.For the HFKmodel,restricted to the history manifold span{|γℓ〉=|ψℓ〉|ℓ〉},the final Hamiltonian takes the form

which is a 1D quantum walk model.Note that it is stoqustic but only in this special history-state basis.A stoqustic Hamiltonian in the standard computational basis cannot be universal.Therefore,we denote 1DQW as the universal resource for AQC.It is obvious that,given more restrictive controllability,the required interaction becomes nonlocal.This is an echo of the resource theory for coherence and correlation that we have established.For resource conversion,it is clear the walk Hwcan be realized or simulated by QCA.The basis transformation from {|ℓ〉} to {|γℓ〉} is also simulated by QCA.

Figure 10.The schematics of a sandwiched circuit which is a special case of that in figure 5.

6.1.Quantum algorithms and resources

In this section,we turn to present a primary resource-theoretic study of some well known quantum algorithms.We mainly focus on algorithms that rely on quantum circuits.In particular,we study the interplay between coherence,interference,entanglement,and contextuality.

For a quantum circuit,we can calculate the amount of interference.We will use I as the notation for interference.We use the relative entropy of coherence.In general,there is no definite relation between I(V),I(W),and I(VW) for two qudit gates V,W ∊U(d).If V is incoherent,then I(VW)=I(WV)=I(W).If an incoherent V is also nonunitary,then I(VW)≤I(W),I(WV)≤I(W),and I(V2WV1)≤I(W) for incoherent V1and V2.An important circuit form is the sandwiched one,shown in figure 10,with the controlled-U gate as a multiplexer defined by equation (34).The control and data registers can be of different dimensions,d1and d2.The interference of CU is the averageFor (V ⊗1)CU(W ⊗1),the relative entropy is the average

For instance,I(CX)=0,I(CX(U ⊗1))=I(U),I(CU(H ⊗1))=1+I(CU).This confirms our intuition.Many algorithms have the sandwiched form of circuit,such as the DQC1 and SWAP-test[127,128].Our study shows that interference is the source for their computational power.

6.2.Van den Nest’s model

In the circuit model,an algorithm on n qubits starts from|0〉⊗nand evolves a circuit U,and the output is obtained by measuring the first qubit in the computational basis with p0as the success probability.Given this,Van den Nest’s model converts to a circuit with one additional qubit,and the final state before measurement takes the form

for ∊∼1/poly(n) as a small error parameter so that the success probability can be boosted efficiently.It was shown that the entanglement is polynomially small,while this model is universal.

We will show that the amount of interference in this model is not small.LetThe interference of the Van den Nest circuit is

for I(V∊)as Cr(V∊)=h(∊)orwhich are close to zero.The major contribution is from the circuit itself I(U),which means the feature of the circuit for solving a problem is preserved.

Therefore,we see by the map from U to Van den Nest’s circuit,the entanglement may change significantly,while the interference does not.This explains why this model works.However,it was argued that entanglement is neither necessary nor sufficient for quantum speedup.Our resource-theoretic study denies this,and it shows that a universal resource needs to be defined in a UQCM.We showed that entanglement or EBIT is the universal resource for LQTM,which is closely related to tensor-network states.As analyzed in section 3.2,entanglement mainly refers to the quantum correlation between parts,while coherence and interference refers to the dynamical change of the amplitudes.In other words,we can put entanglement and interference as orthogonal axis in a coordinate,with entanglement describing static feature of a state,while interference describing how a state evolves.However,entanglement and coherence are also closely related.A crucial fact is that in Van den Nest’s model entanglement is only polynomially small,which can be boosted efficiently,while an exponentially small one cannot be.This means entanglement is indeed still there,and it is more convenient to use interference instead to describe its feature.

6.3.Linear combination of unitary algorithm

In recent years,the LCU algorithm has been developed [53,98–100].Originally,LCU was motivated by the multi-slit interference experiment: a particle,which has two degree of freedoms,namely,pathHpand spinHs,will follow the interference pattern observed on a special screen.The interference is for the particle as a whole.In a LCU task

the Σiciis from the path,but Uiacts on the spin.Its primary component also has the sandwiched form of circuit,probably followed by post-selection.

A caveat is that the interference here is not for amplitudes of states,instead,it is for unitary operators.Actually,we have argued in section 4.1 that this relates to contextuality.The form ΣiciUiis a quantum superposition of contexts each defined by a Ui.This could be a better point of view for LCU and algorithms with the sandwiched circuit.Indeed,the sandwiched circuit is not the one with the maximal amount of interference for the whole spaceHp⊗Hs.A Hamiltonian evolution eiHtor Fourier transformation on the whole space can have larger amount of interference,which can also show quantum speedup,e.g.the quantum walk on special graphs[129].Therefore,we see that although contextuality and coherence are equivalent universal resources,their usages in algorithms could be different.This provides the flexibility for the design of algorithms in different settings.

6.0.3.Shor,Grover,et al algorithms

Shor’s factorizing algorithm has been one of the most significant progresses for quantum computing [4].It is closely related to the algorithms by Deustch–Jozsa,Simons,and the QPE by Kitaev,and solves problems in the class of hidden subgroup [6].Besides some classical side-processing,the primary quantum circuit is of the sandwiched form,which is a contextual circuit from Def.2.Therefore,the resource can be attributed as interference or contextuality.In fact,contextuality is more apparent than interference: the interference of the control register,which enables contextuality,is more crucial.The black-box unitary in the modular exponentiation behaves classically.The quantum Fourier transform is used on the control register whose interference is maximal.

The amount of interference in Deustch–Jozsa algorithm is not extensive,so it does not have exponential speedup over random algorithms.For Simons and Shor algorithm,the final state is in superposition,and the interference is extensive.There is also an extensive amount of entanglement.

From these algorithms,it is clear to see how interference works as the arithmetic of the amplitude.The ‘amplitude arithmetic’ is the additional quantum part beyond classical algorithms.In particular,amplitude can be negative,hence can lead to destructive interference.A quantum speedup occurs when a success probability is boosted by interference based on the amplitude arithmetic.

Grover’s search algorithm[130]demonstrated the power of a different type of quantum algorithms.Despite its oracle setting,it is better described as a qubit rotation in a suitable basis.The rotation angle increase linearly with its iteration.It appears that the amount of interference is not extensive for a qubit evolution [31,36].However,we have to take into account of the basis which would mostly not be the computational basis.As coherence is defined relative to the computational basis,there could be a large amount of interference in Grover’s algorithm.

Grover’s algorithm can be viewed as a state-preparation algorithm.For instance,for a problem to prepare |ψ〉 which satisfies |ψ〉=U|0〉,the interference of U is characterized by the coherence of|ψ〉.For generic state|ψ〉,the quantum speed limit from the uncertainty principle can be used to lower bound the time needed for its preparation [131].This also provides the lower boundfor the search problem of an unstructured database of size N,and proves the optimality of Grover’s algorithm [132].

Recently,Grover’s algorithm has been generalized via‘qubitization’ and quantum singular-value transformation(QSVT) [133,134].Without going into the details,a unitary U is treated as a direct sum of qubit-rotations Uieach for a singular value siin a special basis.Grover’s algorithm is the case with only one singluar value.The interference of U is therefore the average ΣiI(Ui)/d,hence is not extensive.But the coherence for this special basis needs to be considered.This leads to the potential of an extensive amount of interference and a quantum speedup by the QSVT algorithm.

7.Conclusion

In this work,we studied families of universal quantum computing models (UQCMs) using quantum resource theory(QRT).We have shown that QRT offers a rigorous framework to characterize a UQCM and even classify them,and UQCMs serve as broad settings to utilize resources and explore quantum primacy.For each family,we identified a triplet of models.This is not unique and is likely the smallest set of generations.

The quantum circuit model (QCM) indeed is simple and easy to use.It lies at the lowest level in the amplitude family.However,QCM is often found not enough to satisfy more realistic or theoretical needs,such as security,programmability,modularity,controllability,energy efficiency,and parallelism,etc.This requests a diverse exploration of quantum resources and UQCMs.For further investigation,we would like to remark on a few points.

We find many models can be identified by a particular form of circuit.In this work,we have analyzed the transversal,sequential,brickwork,sandwiched,contextual,tailed,and stabilizer circuits.Theses circuits are motivated by the settings of QRT,and each may be suitable to satisfy a particular needs.They can also be used for other purposes,such as quantum speedup [135]and the classification of entangled states.

The comparison and even hybridization of these models are also possible.There can be different perspectives.One way is to use the resource-theoretic method and study the conversion of resources.For instance,the non-commutativity of local Hamiltonian terms shall relate to coherence and entanglement.A more practical way is to take the real physical situations into account.A model may be more convenient in one case but not another;say,if local measurement is not easy to perform,there might not be an advantage to use MBQC rather than the usual circuit model.For a composite task,different models can even be employed to accomplish sub-tasks.

Among the nine UQCMs that we studied,the contextual quantum computing (CQC) and post-magical quantum computing(PMQC)are relatively new.The CQC model relies on our notion of contextuality.However,the landscape of contextuality is a maze [14].There are also schemes or models that utilize contextuality,so it remains to see how these contextual schemes relate and if they can be unified for a consistent notion of contextuality.The PMQC model is the only one that is slightly beyond quantum theory due to the nonlocal box [54].It is not clear if there is a weaker model than PMQC on one hand,and on the other hand,the understanding of the nonlocal world itself[136]is also incomplete.

Our study of the Hamiltonian family is relatively less in depth.We did not study measures of resources and algorithms.However,it implies that this family is equally powerful with other families,and it is worthy to study Hamiltonian-based resources,schemes for fault-tolerance,etc.Also this family does not request automation,i.e.a free evolution eiHtwithout control in the middle.Such autonomous Hamiltonian-based models are also shown to be powerful [66,117–122],hence can be studied further.

We mentioned that,besides the three families we studied,there should also be other families,such as the evolution family,a coding-based family,and even non-universal family for restricted purposes such as communication,metrology,etc[137].In particular,the evolution family relies on the set of quantum channels,the arithmetic on which are known as combs or superchannels [138].The recently proposed quantum von Neumann architecture[64]relies on this and can execute quantum superalgorithms,which can automate the design of a quantum algorithm by another one.We will leave this for future work.

Acknowledgments

This work has been funded by the National Natural Science Foundation of China under Grants Nos.12047503 and 12105343.