Algebro-geometrical orientifold and IR dualities
2023-12-28FedericoManzoni
Federico Manzoni
Mathematics and Physics Department,Roma Tre,Via della Vasca Navale 84,Rome,Italy INFN Roma Tre section,Physics Department,Via della Vasca Navale 84,Rome,Italy
Abstract Orientifold projections are an important ingredient in the geometrical engineering of Quantum Field Theory.However,an orientifold can break down the superconformal symmetry and no new superconformal fixed points are admitted(scenario II);nevertheless,in some cases,dubbed scenarios I and III orientifold,a new IR fixed point is achieved and,for scenario III examples,some still not fully understood IR duality seems to emerge.Here we give an algebro-geometrical point of view of orientifold for toric varieties and we propose the existence of relevant operators that deform the starting oriented Conformal Field Theory triggering a flow.We briefly discuss a possible holographic description of this flow.
Keywords: non-perturbative orientifold,IR dualities,toric geometry,RG flow
1.Introduction
Anti-de Sitter/Conformal Field Theory (AdS/CFT) correspondence is a masterpiece of modern physics: its impact in linking physics and geometry has opened new doors and laid the foundations for new research fields.The original Maldacena AdS/CFT correspondence [1] can be extended to phenomenologically interesting constructions that require 4D SUSY gauge theories with N=1 or N=2 .The starting point is to embed our stack of N D3-branes into a background space-time of the form M3,1×C(X5)where C(X5) is a Calabi-Yau (CY) cone over a Sasaki-Einstein (SE) manifold X5.The geometry properties of the CY define the field theory on the branes but for the general CY cone it is hard to build up the worldvolume gauge theory.We restrict ourselves to the class of toric CY[2–4]since this type of variety allows an algorithmic construction of the field theories.The first example of this kind of AdS/CFT extension is due to Klebanov and Witten in their 1998 pioneering work [5].The toric condition simplifies a lot the geometric description of the CY cone,and indeed all the information is stored in the toric diagram,as we will review in subsection 2.1,and the emerging field theories can be studied using well-established brane tiling techniques [6–12].
In Superconformal Quantum Field Theories (SQFTs),that emerge from the geometrical engineering with the toric CY cone,we can consider the so-called orientifold projections[13–15]that are reviewed in subsection 2.2.The action on the string theory side is to make open-oriented string unoriented and,according to a Chan–Paton-like analysis,real groups such as SO(N) and Sp(2N) are allowed in the emerging SQFTs.In 1995 Polchinski realized [16] that orientifold projections have a simple and elegant interpretation from the point of view of the background space-time: they correspond to not dynamical,mirror-like objects called orientifold planes,defined by T-duality as fixed points of the orientifold projections.On the field theory side,orientifold projection affects fields and superpotential,and its effect can be understood using the brane tiling picture [17].
Let us indicate the orientifold with Ω,and therefore quantities after the orientifold projection will be labelled with the apex Ω.The theory before orientifold is often referred to as the ‘parent’,‘oriented’,‘pre-orientifold’ or ‘unorientifolded’ theory while the one after orientifold as ‘daughter’,‘unoriented’,‘post-orientifold’ or ‘orientifolded’ theory.Similar names hold for quantities in the theories.
The presence of orientifold planes modifies the Renormalization Group (RG) flow,and two different scenarios are mostly investigated in the literature.On the one hand,in scenario I there is a new fixed point and the R-charges of operators that are not projected out are the same as the charges of the corresponding parent theory in the large N limit;this gives us a central charge aΩthat is half the central charge of the parent theory.On the other hand,in scenario II the daughter theory does not have a fixed point.

Despite this,recently in[18,19],a new possibility seems to enter the game:the so-called scenario III.In this case,it is possible [18,19] to construct an orientifold projection such that the central charge aΩis less than half of the central charge a of the parent theory.Moreover,the R-charges before and after the orientifold are not the same.The interesting behavior is that the values of the R-charges and central charge coincide beyond the large N limit,with those of another theory that has the scenario I orientifold.This seems to suggest an IR duality which is in the IR regime because the central charge a gives us,due to c-theorem in 4D,an RG flow ordering of theories.Therefore we know that the scenario I and III orientifolds are lowering the energy moving the theories into their IR regimes.
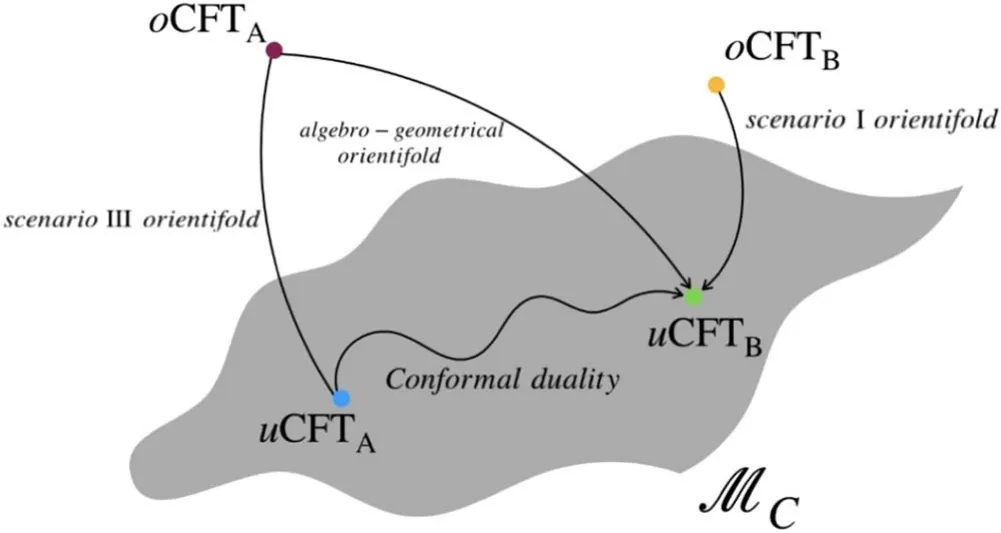
Here we present an algebraic-geometrical interpretation of orientifold,motivated by Greene’s flop transition and the search for a quantum geometry [20–23],as morphisms between algebraic varieties.Orientifolds are thought of as maps that act both on the states of the theory and on the CY cones geometry.The net effect is an RG flow towards the IR regime,from the original oriented model to an unoriented one(see figure 9 to have a schematic picture in mind).
In section 2.1,we review toric varieties and toric CY discussing the construction of manifolds as an algebraic subvariety of the complex space,while in section 2.2 we review orientifold projection and its possible scenarios.In sections 3 and 4 we discuss the algebro-geometrical interpretation of the orientifold and the possible way RG flows triggered by the orientifold itself can be holographically interpreted.
2.Background material: toric geometry and orientifold
2.1.Toric varieties and toric Calabi-Yau
Toric geometry is a branch of algebraic geometry and a toric variety is,by definition,an algebraic variety containing an algebraic torus as an open dense subset,such that the action of the torus on itself extends to the whole variety.To be more specific,an n-dimensional toric variety M has an algebraic torus action in the sense that the algebraic torus Tn=(C *)nis a dense open subset and there is an action Tn× M →M.The greatest point in favor of toric geometry is that the geometry of a toric variety is fully determined by combinatorics.
In the case of a toric CY variety,the information about the geometry is summarized in the so-called toric diagram which is a polytope embedded in an-1Z -lattice.Moreover,when we consider a toric CY threefold cone the action of the algebraic torus enlarges the isometry group of the variety from U(1),the action induced by the Reeb vector field,toU(1 )3.Let us briefly review some possible constructions of toric varieties [2–4].
Figure 2.Examples of fans.Left: fan of CP1 ×CP1,we have four one-dimensional SCRPCs (the vectors) and four two-dimensional SCRPCs (the quadrants).Right: fan of CP 2,we have three onedimensional SCRPCs (the vectors) and three two-dimensional ones(the trians).
2.1.1.Homogeneous coordinates approach to toric varieties.The simplest way we can image toric variety is as a generalization of weighed projective space [24].Let us recall first the definition of the (m-1)-dimensional weighed projective space
where the quotient by *C is taken into account by the identification (z1,…,zm)~whereλ∊C* and(i1,…,im) are the so-called coordinates weights.An ndimensional toric variety M is the generalization where we quotient by more than one *C action and the set that we subtract is a subset UΣwhich contains not only the origin
where Γ is an abelian group.This variety has an algebraic torus action given by (C*)m-m+n=(C *)n.Definition (2)emerges in the context of cones and fans that we are going to discuss.
Let M and N be dual n-dimensional lattices isomorphic tonZ and consider the vector spacesMRandNRto be the subspace ofnR spanned,respectively,by vectors in M and N.We define the Strongly Convex Rational Polyhedral Cone(SCRPC)σ∊NR⊂Rnas the set

for a finite number of vectors viand satisfying the condition(σ)∩(-σ)={0}.Let us analyze this definition:we consider an n-dimensional latticeNn≃Z,a SCRPC is an n or lower dimensional cone inNRwith the origin of the lattice as its apex,bounded by hyperplanes (polyhedral) with its edges spanned by lattice vectors (rational) and such that it does not contain complete lines(strongly convex).The dimension of a SCRPC σ is the dimension of the smallest subspace ofnR containing σ.Two important concepts are useful in SCRPC theory:
• edges: these are the one-dimensional faces of σ,the vectorsassociated with the edges are the generators of σ;
• facets: these are the codimension one faces.
A collection Σ of SCRPCs inNRis called a fan if each face of the SCRPC in Σ is also an SCRPC in Σ and the intersection of two SCRPCs in Σ is a face of each.Examples of SCRPCs and fans are reported in figures 1 and 2.
Let us consider a fan Σ and we call Σ1dthe set of onedimensional SCRPCs;letwith i=1,…,m be the whole set of vectors generating the one-dimensional SCRPCs in Σ1d.1Note that obviously,m is equal to the number of one-dimensional cones and so to the number of elements in Σ1d.To each vectorwe associate a homogeneous coordinatezi∊C and we define the set
where the union is taken over all the sets having I ⊆{1,…,m}for which ziwith i ∊I does not belong to an SCRPC in Σ.
At this point,we need to discuss how the (C*)m-n× Γ acts onmC .First of all,let us clarify the nature of the abelian group Γ: this is given by

Figure 4.Toric diagram of the conifold.
Let us now discuss the algebraic torus (C*)m-naction.Consider the n×m matrix build-up considering the m vectorswith n components
this induces a mapφ: Cm→Cndefined by
Thanks to the rank-nullity theorem2Given T a linear map between two finite dimensional vector spaces A and B we have thatdim (I m (T )) +dim (K er (T))=Rank (V )+Null (V )=dim (A).In our case we know that with i=1,…,m are m linearly independent vectors so Rank (V )=dim (I m (T ))=m.the dimension of the Kernel of map (7) must be m-n;we can identify it with(C*)m-n.It is now simple to see how (C *)m-nacts on Cm:each *C action is taken into account by
withλ∊C* .We have m-n actions like(8),where for each a=1,…,m-n the charge vectorsbelong to the Kernel of the map φ and therefore must satisfy m-n relations
Quotient (C*)m-nout means taking into account the equivalence relations
for a=1,…,m-n.
To summarize,we can define the toric variety as
this is an n-dimensional variety,with a residual(C *)n≃U(1)naction and the (C*)m-naction is quotient out by m-n relations(10)with weights that satisfy relations(9).Let us give an example.
2.1.2.Example: CP2.Let us consider the right fan in figure 2: this is a Z2lattice;we have the three vectorsthat generate onedimensional cones.We have three homogeneous coordinates(z1,z2,z3) ∊C3and the set UΣis given by the origin.Since m=3 and n=2 we must have one *C action and we can find the weights using (9):
as we expected.
We now give some interesting properties about toric varieties and their fans:
• a fan Σ is smooth if every SCRPC in Σ is smooth,an SCRPC is smooth if is generated by a subset of a basis ofN≃Zn;
• a fan Σ is simplicial if every SCRPC in Σ is simplicial,an SCRPC is simplicial if it is generated by a subset of a basis of Rn;
These conditions are important since if a fan is smooth the corresponding toric variety also is smooth and if a fan is simplicial then the corresponding toric variety can have at most orbifold singularities.We see immediately that the two spaces described by the fans in figure 2 are smooth since every SCRPC is generated by a subset of a2Z basis.An example of toric variety with orbifold singularities is the weighted projective space CP2,3,1;its fan is given in figure 3 below.Orbifold singularities can be removed by the so-called blow up procedure: roughly speaking,for an n-dimensional toric variety we replace the singular locus with
Let us now specialize to the case of our interest: CY threefolds.First of all,we have anU(1)3≃ (C*)3action but there is more:the condition of trivial canonical bundle implies that all the vectors of the fan belong to the same hyperplane,so we can project on this hyperplane obtaining a twodimensional object whose convex hull takes the name of toric diagram.The CY condition implies
We have m-n=4-3=1 charge vector given by relation (9):
and a possible solution is Q=(-1,1,1,-1).As one can note the CY condition is automatically implemented by the fact that the vectors are coplanar.The action of the algebraic torus *C is quotient out by the equivalence relation
Let us consider the *C -invariant polynomials:by(16)we note that
are invariant and this is the minimal basis with which to write all the *C -invariant polynomials.However,note that these polynomials are not independent but they must satisfy the relation
which is the defining polynomial of the conifold [5].
and so Q=(-2,0,1,1).Since we have one vanishing component,Q2=0,the coordinate z2has no role and so we will expect a CY toric manifold of the formX× C,where X is unknown for the moment andC is the space associated to z2.We have the equivalence relation
since on z2the algebraic torus action is trivial we do not consider it and so we must find m-1=4-1=3 *C -invariant polynomials,for example
and they satisfy the relation
The general algorithm to identify to which variety a toric diagram belongs is the following: given the toric diagram we look at the equivalent relations that quotient out the algebraic torus action (C*)m-nand we construct a minimal basis of m(C*)m-n-invariant polynomials;the m-n relations that these polynomials must satisfy identify the toric variety as subvariety ofmC .
2.1.5.Moment maps approach and Delzant-like construction.Let us take a step back and consider a different way to define toric varieties.Let M be a symplectic manifold of real dimension 2n with symplectic form ω.Given the actionU(1)n× M → Mthis is said to be Hamiltonian if its restriction to anyU1U1n
()⊂ () is Hamiltonian and any two of them commute.In this context the so-called moment map :Mn μ→R emerges,whose components are the Hamiltonians of each U(1) action.Since all the U(1)commute,for any∊Rn,its preimageμ-1is invariant under the action of the fullU1n() .Moreover,if M has a Kähler structure,the existence of the Hamiltonian action implies that the isometry group contains the algebraic torusU(1)n≃ (C*)n.So a toric variety emerges in a simple way as a real 2n dimensional symplectic manifold M that has a Hamiltonian action of the algebraic torus on it.3There is a little caveat: if M is a cone the algebraic torus action must commute with the homothetic action induced by the Euler vector field.
We are interested in non-compact toric varieties but let us talk a little about compact ones.If M is compact,Delzant[25] showed that the image through the moment map of the variety,μ(M),is a convex polytope Δ called Delzant polytope;however,we are interested in CY cones,i.e.noncompact toric varieties.The generalization to a Deltzan-like construction is possible[26]but the image under the moment map is no longer a polytope but a cone:
and its dual graph is still a fan generated by the normal vectorsCY condition imposes thatare coplanar so we can project out the common component and get an (n-1)-dimensional object that encodes the geometry: the toric diagram.Since the components of the vectorsare integers,the toric diagram is the convex hull of a set of points in a Zn-1-lattice.In the Deltzan-like approach,the toric variety is built up using the Kähler quotient and the toric variety is aU(1)nfibration over Θ: oneU(1) ⊂U(1)nshrinks on the edges and so acts trivially,moreover,since in a vertex n edges meet each other,the fullU1n() fiber shrinks.Hence the vertexes are the fixed loci of the full algebraic torus action.It is interesting to note that this construction is well known by physicists: this is the moduli space of the Gauged Linear Sigma Model (GLSM),it is a SUSY gauge theory with abelian gauge groupU(1)m-nand m chiral superfields Z1,…,Zmwith charges Q1,…,Qm-nunder the m-n U(1).
In the case of our interest,namely CY threefold,the toric diagram is a two-dimensional object and the CY cone threefold exhibits a three-dimensional algebraic torus action.From the toric diagram,we can get information on the dual QFT using the five brane system and brane tiling constructions;moreover,we can calculate some useful quantities of the dual field theory directly from the toric diagram,such as the central charge,using the Butti and Zaffaroni procedure[27] or the symplectic decomposition procedure [28].
2.2.Orientifold projections
Denoting by 0 ≤σ ≤π the coordinate describing the open string at a given time,the two ends σ=0,π contain,thanks to Chan-Paton indexes,the gauge group degrees of freedom and the corresponding charged matter fields.At the endpoints,we can apply Dirichlet or Neumann boundary conditions and we know that under T-duality these are interchanged.Orientifold projections of Type IIB theory are obtained by projecting the Type IIB spectrum by the involution Ω (Ω2=1),exchanging the left and right closed oscillatorsand acting on the open strings as phases:
The overall effect is that orientifold projections map oriented strings to unoriented ones and type I superstring theory is nothing but an orientifold projection of type IIB superstring theory [29]:type
Orientifold introduces,from the worldsheet point of view,new surfaces in the Polyakov topological expansion.Indeed,due to the presence of unoriented strings,nonorientable surfaces such as Klein bottles or Möbius strips are allowed.From the space-time viewpoint,these correspond to not dynamical objects,called O-planes,defined by T-duality as fixed points of the orientifold projection [30].
However this picture is not the complete one since,nowadays,there are no results in actual string theory for what one might expect to be the curved back-reacted geometry of orientifold.Indeed as reported in [31],for any solution with O-planes,the presence of such a plane is inferred by comparison with their flat-space behavior.However,since the orientifolded space times have strong curvature and coupling,stringy corrections come into play,and it is impossible to decide with supergravity alone whether the solutions are valid.Therefore,it is natural to think of more general behaviors in which geometric phase transitions due to the presence of an orientifold can play a crucial role.Since this kind of behavior is highly non-perturbative we expect something to happen in the field theory that goes beyond the large N limit.
This orientifold construction has important consequences on the emergent field theory build up with the AdS/CFT and toric CY machinery: some degrees of freedom are projected out and orthogonal and symplectic groups are now allowed together with symmetric and antisymmetric representations of unitary groups.The rules for the construction of these kinds of theories are studied for example in[17,32–34].The crucial point here is that orientifold can give rise to different scenarios:
• in scenario I there is a new superconformal fixed point and the R-charges of the operators that are not projected out by Ω are the same as the charges of the corresponding one in the oriented theory and in the large N limit.In the end,the post-orientifold central charge aΩturns out to be half of the pre-orientifold central charge a;
• scenario II does not admit a new superconformal RG fixed point;
• in scenario III there is a new superconformal fixed point but the R-charges of the operators that are not projected out by Ω are different from the charges of the corresponding one in the oriented theory and not only at large N.In the end,the post-orientifold central charge aΩturns out to be less than half of the pre-orientifold central charge a.However,something very interesting happens here:this could be(one of)the right field theory dual to the non-perturbative action of orientifold in the string theory side.
2.2.1.The scenario I orientifold.The scenario I orientifold occurs when the pre and post-orientifold R-charges of the theories are the same and the central charge post-orientifold is half of that pre-orientifold:
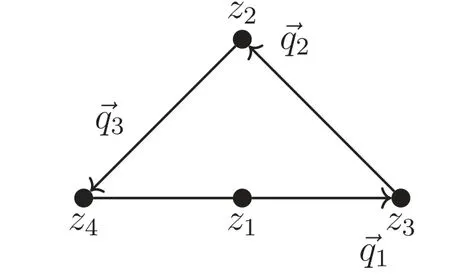
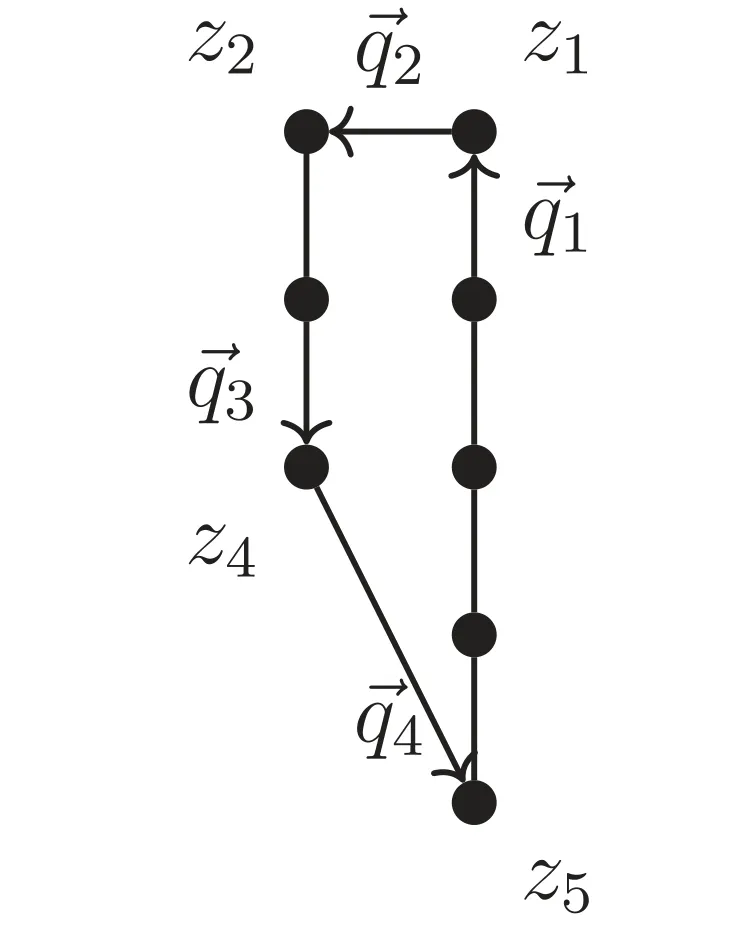
The CY cone describing the theory before and after the orientifold is then the same but with different volume due to the orientifold action.Moreover,due to the c-theorem in 4D,according to which aIR 2.2.2.The scenario II orientifold.Scenario II seems to be quite trivial: there is no new superconformal point and the orientifold breaks conformal symmetry.However,as known in the literature,these situations can give rise to a duality cascade or conformal symmetry can be restored with flavor branes [35]. 2.2.3.The scenario III orientifold and the IR duality.In the scenario III orientifold,the pre and post-orientifold R-charges of the theory are not the same and the post-orientifold central charge is less than half of that pre-orientifold [18,19]: In this case the CY cones describing the theory before and after the orientifold are not the same.Scenario III orientifold seems to be part of a bigger picture where geometry/topology transitions play a crucial role.Note that,since the c-theorem in 4D tells us that aIR The IR duality we are talking about was recently proposed in[18] studying the orientifold projections of Pseudo del Pezzo models (PdP) and subsequently extended to an infinite class of models in [19].Given two different oriented models oCFTAand oCFTB,which have nothing to do with one another,it turns out that the existing orientifold projections are such that the R-charges,central charges and superconformal indexes of the two unoriented uCFTAand uCFTBmodels are the same [18,19] This suggests the proposed duality and since orientifold leads to the IR regime,this is an IR duality.More specifically the oCFTAhas a scenario I orientifold while the oCFTBhas a scenario III orientifold and the set of R-charges,central charges and superconformal indexes of the two unoriented models are the same for any finite value of N.What we have said in words is summarized in the following scheme.Some examples of the IR duality due to orientifold in scenario III seems to be explained and interpreted,from the field theory point of view,in terms of inherited S-duality from the N=2 case.The authors observe that the duality for the N=1 models discussed in [19] corresponds to S-duality at different points of the conformal manifold[36–38].Therefore the duality between the two unoriented models can be thought of as a conformal duality.The crucial property behind this result is the presence in the spectrum of two-index tensor fields with R-charge equal to one,uncharged with respect to the other global symmetries. Our main goal is to better understand the link between orientifolds and the IR duality from the point of view of the geometry.The guiding ideas are the flop transition and the other geometry/topology changes in string theory compactifications,where the geometry/topology of the CY manifold are modified due to a quantum behavior of the geometry itself[20–23].Heuristically,one suspects that geometry/topology might be able to change by means of violent curvature fluctuations,such as induced by an orientifold,which would be expected in any quantum theory of gravity.Therefore,the basic idea is that orientifold projections map the algebraic equations describing the geometry of the CYAinto those that describe the geometry of the CYB.This orientifold modifies the geometry of the CYAcone due to its intrinsic non-perturbative nature and this geometrical change induces k new degrees of freedom with R-chargesa˜ito emerge(we will call them orientifold-mapping operators or oμ-operators).They make the original field theory no longer fulfilling the conditionhence old R-charges aiand oμoperators R-chargesmust mix together to return a set of new R-chargesconsistent with the modifiedcone geometry,that is now CYBcone,and satisfying the condition=2.The steps are summarized in the following scheme.chagres associated with extremal points matter,in the first case the two oriented theories have the same number of Rcharges while in the second case the number of R-charges of the oriented theories are not equal and we expect that some not extremal points of the toric diagram of theory A became extremal points after the orientifold action.Cases with ΔPe>1 are not discussed in this work since no examples have been found;they may be studied in future works to better understand the link between geometry,orientifold and the IR duality. Figure 5.Toric diagram of The interpretation of an orientifold in this way will be called an algebro-geometrical orientifold.This orientifold is different from scenario I and III orientifolds because,referring to scheme (29),the latter acts horizontally while the former acts crosswise from the oriented model A to the unoriented model B.This kind of orientifold implements the IR duality from the geometric point of view as morphism between CY algebraic varieties. In the following subsection,we study these two cases with specific examples but this construction can be repeated for many other pairs and the result is that it is always possible to construct relevant operators with the new degrees of The procedure is as follows:from toric diagrams of theories A and B we determine the sets of algebraic equations using toric geometry tools exposed in section 2.1;then we map these two sets into each other and,finally,we associate at every homogeneous coordinate zia trial R-charge,adding the minimal number of new degrees of freedom.The analysis must consider two different cases: Let us consider the conifoldC andfor toric diagrams and toric data.We refer to examples in subsection 2.1.4.Moreover,in those examples determination of the equations that describe the CY cones has already been done.The conifold has scenario I orientifold whilehas scenario III orientifold and the two theories are IR duals.The set of equations for the two theories are Now we have to map the two equations in all possible ways remembering that after the orientifold action the toric diagrams are mapped into each other and so the coordinates ziare effectively the same.However,if we want to keep track of the different R-charges associated to the homogeneous coordinate ziof the two different toric diagrams so the R-chargesbi=and ai,we must remember that we have to associate a different set of R-charges at those zibelonging to different equations and so different theories.We have to consider the following mappings: By associating the set of oriented R-charges {z1,z2,z3,z4}→{0,a2,a3,a4} to the zicoordinates of Yipolynomials and the set of oriented R-charges{z1,z2,z3,z4}→{b1,b2,b3,b4} to the zicoordinates of Xipolynomials,we get the following relations: and they are not all independent.If we make together systems I,II,III and IV we obtain the following relations: and we have also the relation.These conditions are not sufficient to fix unequivocally the values of the Rcharges to those of the conifold.However this is right,indeed using the fact we know the values at the superconformal fixed point of the two sets of R-charges,namely {a1,a2,a3,a4}={0,2/3,2/3,2/3}and{b1,b2,b3,b4}={1/2,1/2,1/2,1/2},we may note that the equations (32) do not do the right job.Nevertheless,if we admit the existence of a new operator (an orientifold-mapping operator) with R-chargewe note that,for example, Figure 6.Toric diagram of with the useful vectors to associate fields and R-charges. now we have the right matching. Finally,let us now consider the fields associated toand their R-charges [27,28]. Referring to figure 6 we have Hence we have 2 fields with R-charge a3,2 fields with Rcharge a2,1 field with R-charge a4and 1 field with R-charge a4+a1.Despite in the oriented theory,charge a1does not play any role,here,in the unoriented one,we can identifya1≡and so there is a field with a new R-charge due to orientifold action;we call it Π.4Its bosonic part will be dubbed puppon while its fermionic,one puchino.This field is the one associated,according to [27] or [28],to the R-charge given by the combination of the new charge entered in the game,a˜,and the other charges.It is interesting to note that field Π associated with the R-chargehasR=a4+=1.We can build up a relevant deformation with Π,for exampleOi=iφ Π where Φiare the other chiral fields with R-chargeThe scaling dimension ofOiis given byThis makes sense given that orientifold has the effect of making the theory flow into the IR regime;so this operator turns on and the theory becomes IR dual to another theory that has the correct set of R-charges to match systems (32). Figure 7.Toric diagrams of (right) and L(3,3,3) (left). One may wonder since the mapping is not one-to-one;however this seems to be a peculiarity of very symmetric models described by highly symmetric toric diagrams with a small number of points.Indeed in the case ofC andthere are exactly four ways of superimposing the two toric diagrams so as to place the greatest number of points of the two diagrams in the same position.From the field theory point of view,this ambiguity is probably due to the flavour global symmetries of the models since in both the set of R-charges the R-charges themselves are identical. To determine the set of equations describing the two varieties we follow the step highlighted in section 2.1. where a=1,…,5.Solution space can be parameterized as follows: the equivalence relations are given by For L(3,3,3)we follow the same steps.We have m-n=8-3=5 charge vectors solution of where a=1,…,5.Solution space can be parameterized as follows: the equivalence relations are given by Let us now proceed with the matching between sets (39) and(43).Since we have ΔPe=0 we can not consider all the not extremal zi,indeed we expect that no new point enters the game.We note that if we match the first three polynomials of the two sets we get automatically that all other polynomials match,so In this case we do not have an obvious candidate to play the role of Π since no new extremal point enters in the game.Despite this,we can construct relevant operators that perturb the conformal theory and induce the RG flow to the dual theory in the IR.As in the ΔPe=1 case,we add the new Rcharge to the point that must be moved to transform the toric diagram ofinto the toric diagram of L(3,3,3),namely z5.Therefore Π is a field with R-chargeand a relevant operator can be constructed,for example,as Oi=Πiχwhere χiare the two fields with R-charge R[χi]=a1+a2.The scaling dimension ofOiis given by In this case,we have only one matching which is suggested by the fact that we have only one way of superimposing the two toric diagrams so as to place the greatest number of points of the two diagrams in the same position.Indeed the toric diagrams are less symmetric with respect to the case ofC andand the field theories have less flavour global symmetries. In section 3 we have shown that,assuming the orientifold is able to change the geometry by transforming the CYAcone into the CYBcone we are forced to consider relevant operators which induce an RG flow that we know must end in a new superconformal fixed point.In holography,we are able to build up gravity solutions that are dual to RG flows [39]. Following the same steps of the case ΔPe=1 we can associate R-charges to the fields of theory Referring to figure 8 we have Let us consider a set of scalar fields φain an AdS5background with coordinates (x0,x1,x2,x3,z)5We are going to use Greek indices for 4-dimensional quantities and capital Latin indices for 5-dimensional ones.and action given by We assume a 4D Poincaré invariant metric of the form ds=dz2+e2Y(z)dxμdxμ,known as the domain wall ansatz,that we recognize as the Poincaré patch AdS with a radius R if the warp factor is a linear functionand using the redefinitionFields equations read an obvious solution is given by the negative critical points of the potential Vcritand a set of constant scalars, then the second equation is trivially satisfied while the first gives usUp to coordinates redefinition,we can then write as This is nothing but AdS with its radius controlled by the critical point of the potential.Now we can expand the action around this solution and we can infer the conformal dimension of a CFT operator Oafrom the masses of the quadratic fluctuations ma, At this point we are looking for more generic solutions that are asymptotically AdS;we will consider solutions that have the linear warp factorand constant φanear the boundary at z →∞and in the deep interior for z →-∞.This is conjectured to be dual to an RG flow from a UV fixed point to an IR fixed point.It is natural to identify the radial coordinate z with the field theory RG scale viathis choice guarantees that in the UV,at the AdS boundary,we have μ →∞for z →∞,while in the deep interior we have μ →0 for z →-∞.As we know the exact identification of the RG scale is scheme dependent and a particular choice of coordinates on the supergravity side corresponds to a particular choice of renormalisation scheme on the field theory side.Said in another way,our goal is to find an interpolating flow solution of (46) which interpolates between two stationary points.In AdS/CFT language,this means that we are looking for a domain wall solution interpolating between an AdS space of radius RUVfor z →∞and another AdS space of radius RIRfor z →-∞.At the same time,the scalars φaare expected to flow from a constantφaUVin the UV to a constantφaIRin the IR.A domain wall solution of this type is expected to be dual to a field theory RG flow between two conformal theories. Since for z →±∞we have an AdS space-time we can use the holographic dictionary: on the boundary and in the deep interior region the scalars behave as in which Aais the source of Oaand Bais its VEV.If Aa≠0 the solution describes a deformation of the CFT by operator Oawhile if Aa=0 and Ba≠0 it describes a different vacuum of the CFT where the operator Oadevelops a non-vanishing VEV.In both cases,conformal invariance is broken and an RG flow is triggered;the gravity solution is dual to this RG flow. Figure 8.Toric diagram of with the useful vectors to associate fields and R-charges. Particularly interesting is the case in which the Oaoperator is relevant and the RG flow leads to a new fixed point and this is possible if and only if the potential V(φ)has more than one critical point (in such a way that another AdS solution with different radius is possible);the gravity solution is a kink interpolating between the two critical point AdS solutions.In order to have an RG flow that starts from a CFTUVwe need a relevant operator (very similar to what happens in IR duality linked to the algebro-geometrical orientifold) and to hit a CFTIRwe need the operator to become irrelevant there.Looking at the mass-dimension formula this means that in the relevant operator case,the squared mass of the scalar fluctuation must be negative (a maximum of the potential V(φ)) while in the irrelevant operator case,the squared mass must be positive(a minimum of the potential V(φ)). The construction of holographic dual of RG flows could be applied to explain the IR duality arising from algebrogeometrical orientifold.We have seen how the duality requires the presence of relevant operators that deform the initial CFT associated with the CYAcone into the CFT associated with the CYBcone.In the spirit of the toy model presented above,this entire IR duality mechanism could be interpreted as the holographic dual of a suitable effective supergravity solution that has to interpolate between the supergravity solution of oriented model A and the supergravity solution of unoriented model B.Let us label the oriented models as oCFTAand oCFTBwhile the unoriented models as uCFTAand uCFTB.If we are able to perform the Kaluza–Klein (KK) reduction on the SE base manifoldsandwe get two gauged supergravity descriptions with two different potentialsWe expect these two gauged supergravity theories are consistent truncations of type IIB superstring theory,respectively,onwith gauge groupand ongauge groupThis is in analogy with the FGPW flow [40],which is the holographic description of the Leigh–Strassler RG flow [41] of N=4 SYM theory.Moreover,as in the FGPW flow and according to AdS/CFT philosophy,we expect the gauge groups to be given by the isometry groups of the SE bases. The flow would be holographically described if we are able to find a suitable supergravity description with a potential that has several critical points.The maximum of the potential has to preserve the originalsymmetry while another critical point has to preserve thesymmetry.However,this kind of approach poses technical and conceptual challenges.First of all the KK reduction on the compact Sasaki-Einstein manifold X5is far more difficult than for S5.Therefore,it is not easy at all to build up explicit potentials for these supergravity descriptions.Moreover,from the conceptual point of view,the supergravity description cannot be the full story since the orientifold is non-perturbative.The supergravity description has to be uplifted in a full string theory description which must match with the string theories associated with the two CFTs A and B.Anyway,it is not clear if such a suitable supergravity model exists but if so,we will have a holographic description of the flow induced by the algebro-geometrical orientifold itself and further investigation on this point will be part of future research works. Orientifold projections give the opportunity of new possibilities for the creation of field theory models from a string background called unoriented models [13].The appellation‘unoriented’is mainly due to the action of the orientifold map on the string oscillators: the involution makes an oriented string an unoriented one and a Chan-Paton-like analysis suggests the possibility of a new gauge group like SO(N)and Sp(2N).However,orientifold behaviour is inferred by comparison with the flat-space behavior but,probably,orientifolds have an intrinsic non-perturbative nature [31].This is also suggested by a recent interesting new feature proposed in[18] and expanded in [19]: the so-called scenario III.What happens is that a theory after a scenario III orientifold shares the same R-charges,central charge and superconformal index of another orientifolded theory coming from a scenario I orientifold.The crucial point is that these physical quantities are the same not only in the large N limit but for every N[18,19]: this is a non-perturbative effect.Since the physical quantities are the same in the IR we refer to these theories as IR duals and,since in geometrical engineering,the field theory depends on the geometry of the CY cone,these two orientifolded theories can be considered to have the same CY cone geometry.This means that a change in the geometry of the cone has to happen due to the orientifold action.The change,due to the orientifold,can be traced back to the equations that describe the algebraic CY varieties and we require the matching between these sets of equations.In this sense,the orientifold has an algebro-geometrical interpretation as a morphism between algebraic varieties given locally by polynomials.This interpretation has as its guiding idea the flop transition and the other geometrical change in string theory compactifications[20–23].The properties and a deeper understanding of this interpretation,such as the answers to the questions:‘Are orientifold regular maps or rational maps?Are they biregular or birational?’could be fertile ground for future works.We stress that if orientifolds are such kinds of maps for the CY cones,they open the door to the use of the theory of category with orientifolds as morphisms and field theory as objects.Therefore,an orientifold acts both on string states and on the geometry of the space-time. Figure 9.Schematic picture of the RG flow triggered by the orientifold action.The little‘o’stays for‘oriented’while the little‘u’stays for ‘unoriented’.The two unoriented models lie on the same conformal manifold while the two oriented models are not related in any way.The flow triggered by the algebro-geometrical orientifold action links the oriented model A to the unoriented model B. From the requirement of the matching between these sets of equations describing the CY cone of the two theories and using some tools of algebraic geometry and toric geometry,reported in 2.1,we infer the existence of relevant operators that deform the initial CFT triggering an RG flow towards the IR regime.A schematic picture of the flow is given in figure 9.The flow could be described using a holographic dual,whose toy model is presented in 4.1,but the prohibitive KK reduction on the base of a generic CY cone makes the explicit construction difficult.Moreover,due to the intrinsic non-perturbative nature of orientifold,this supergravity dual is expected to be only an effective description that must necessarily be uplifted in full string theory. Acknowledgments We thank first of all Prof.Fabio Riccioni for inspiring the present work and Prof.Massimo Bianchi and Salvo Mancani for interesting discussions.We also thank Davide Morgante for the discussions and comments and Matteo Romoli for their reading of the manuscript and comments.Special thanks to Maria Luisa Limongi who supported the work.3.Algebro-geometrical orientifold and IR dualities
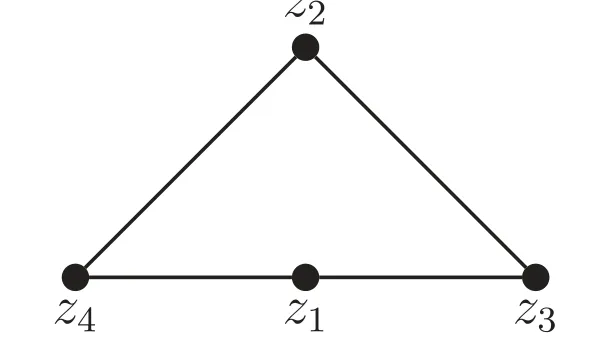
3.1.Different number of external points: ΔPe=1

3.2.Equal number of external points: ΔPe=0
4.Brief discussion on the holographic dual
4.1.The toy model for holographic duals of RG flows and beyond
5.Conclusion
杂志排行
Communications in Theoretical Physics的其它文章
- Disassociation of a one-dimensional cold molecule via quantum scattering
- Particle dynamics,black hole shadow and weak gravitational lensing in the f (Q) theory of gravity
- Heat engines of the Kerr-AdS black hole
- Macroscopic squeezing in quasi-onedimensional two-component Bose gases
- Stable bulk nanobubbles can be regarded as gaseous analogues of microemulsions
- A significantly enhanced magnetic moment due to an electric dipole moment
