Propagation of chirped solitons on a cw background in a non-Kerr quintic medium with self-steepening effect

Abdesselam Bouguerra ,Houria Triki ,Chun Wei ,Zhenbang Lu and Qin Zhou,∗

1 Radiation and Matter Physics Laboratory,Matter Sciences Department,Mohamed-Cherif Messaadia University,P.O.Box 1553,Souk-Ahras,41000,Algeria

2 Radiation Physics Laboratory,Department of Physics,Faculty of Sciences,Badji Mokhtar University,P.O.Box 12,23000 Annaba,Algeria

3 School of Electronics and Information Engineering,Wuhan Donghu University,Wuhan 430212,China

4 School of Mathematical and Physical Sciences,Wuhan Textile University,Wuhan 430200,China

Abstract We study the existence and stability of envelope solitons on a continuous-wave background in a non-Kerr quintic optical material exhibiting a self-steepening effect.Light propagation in such a nonlinear medium is governed by the Gerdjikov–Ivanov equation.We find that the system supports a variety of localized waveforms exhibiting an important frequency chirping property which makes them potentially useful in many practical applications to optical communication.This frequency chirp is found to be crucially dependent on the intensity of the wave and its amplitude can be controlled by a suitable choice of self-steepening parameter.The obtained nonlinearly chirped solitons include bright,gray and kink shapes.We also discuss the stability of the chirped solitons numerically under finite initial perturbations.The results show that the main character of chirped localized structures is not influenced by finite initial perturbations such as white noise.

Keywords: solitons,non-Kerr nonlinearity,self-steepening effect

1.Introduction

The dynamics of envelope solitons in dispersive nonlinear media have attracted increased interest in recent years [1–4].Such localized wave packets can propagate in nonlinear dispersive media without any change in their shape over extremely large distances.The formation of these localized waves in single-mode fibers occurs when the pulse broadening of the groupvelocity dispersion and the compressing of the Kerr nonlinearity are exactly balanced[5].Because of their extensive applications to optical communication and all-optical ultrafast switching devices[6],soliton structures have recently become the subject of intense study,especially in the field of nonlinear optics[7,8].

The main envelope equation that governs the transmission of a soliton pulse inside an optical waveguiding medium is the cubic nonlinear Schrödinger (NLS) equation,which incorporates the terms representing the effects of group velocity dispersion and self-phase modulation [9].It is worth mentioning that such a model equation rigorously describes the evolution of low-power pulses with durations of a few picoseconds in optical fibers.Within this NLS equation framework,two distinct types of localized solutions,the socalled bright and dark solitons,were shown to exist in the anomalous and normal dispersion regimes,respectively[2].It is noteworthy that such fundamental solitons are chirp-free pulses because the chirp produced by group velocity dispersion is balanced by the chirp produced by the Kerr nonlinearity [10].However,if short pulses have to be injected into the optical material,higher-order effects become important and should be incorporated into the underlying equation.In such a situation,the pulse dynamics can be described by more generalized NLS equations containing various contributions of higher-order dispersive and nonlinear terms.Such equations were found to have a rich variety of soliton solutions [11–13],which may be useful in understanding different physical phenomena and dynamical processes arising in optical systems.We note here that important results have been found with recent works demonstrating soliton dynamics supported by complex parity-time symmetric potentials [14] as well as breathers and rogue waves in spinor Bose–Einstein condensates with space-time modulated potentials [15].In addition to nonlinear waveforms,optical characteristics of a new type of materials that have application prospects in the field of nonlinear optics have been also reported [16].

Recently,much attention has been directed toward the study of nonlinearly chirped soliton pulses in optical fibers and waveguides[17–22].This is because chirp is very useful in the process of light pulse compression and has potential applications in optical communication systems [23].Notably,chirped pulses are useful in the design of optical devices such as fiberoptic amplifiers,optical pulse compressors and solitary wavebased communication links[18,24].Physically,the chirp of an optical wave is generally known as the time dependence of its instantaneous frequency [10].In this setting,significant results have been obtained with recent studies analyzing the propagation of nonlinearly chirped solitons in optical materials exhibiting different kinds of higher-order effects such as selfsteepening and self-frequency shift processes [18],self-steepening and quintic nonlinearity [17,19,20],self-steepening and quintic-septic-nonic nonlinearities [25].However,all chirped soliton solutions mentioned above are obtained under the influence of cubic nonlinearity.How to find the exact and new kind of chirped solitons in the absence of cubic nonlinearity is interesting work.Such a problem is addressed and clarified in the present work.We demonstrate here that under the vanishing Kerr nonlinearity,different chirped soliton solutions on a cw background are formed in a non-Kerr quintic medium exhibiting a self-steepening effect.In particular,different types of bright,gray,kink solitons on a cw background are found for the first time for the so-called Gerdjikov–Ivanov equation,which is a kind of NLS equation modeling the wave dynamics in the presence of quintic nonlinearity and selfsteepening effects.We will show that under the influence of the self-steepening process,these envelope solitons acquire a frequency chirp that depends strongly on the wave intensity.

The paper is organized as follows.In section 2,we present the general form of the nonlinearly chirped traveling wave solutions of the Gerdjikov–Ivanov model and their corresponding frequency chirp.In section 3,we find a variety of exact chirped soliton solutions on a cw background for the governing equation and determine the chirp associated with each of these soliton structures.In section 4,we analyze the stability of our chirped solutions against small perturbations such as white noise.Our findings are summarized in section 5.

2.General traveling wave solutions

The Gerdjikov–Ivanov equation governing the propagation of the optical field in a non-Kerr quintic medium exhibiting selfsteepening nonlinearity can be written in the form [26–30]:

where q is the complex amplitude of the electric field,x is the distance and t is the time.Parameters α,β and γ represent the group velocity dispersion,self-steepening effect,and quintic nonlinearity,respectively.

Model (1) has been used to study stationary solutions by applying the Lie symmetry method[26].The conservation laws for equation (1) have also been derived by means of Lie symmetry analysis[27].In addition,soliton-like solutions have been obtained with the application of Madelung fluid description[28].Moreover,the explicit soliton-like solutions of the Gerdjikov–Ivanov model have been derived by employing its Darboux transformation [29].Several exact localized solutions including bright,kink,and singular soliton solutions have been also found for this model[30].Here,we will find the soliton solutions on a cw background which exhibit a nonlinear frequency chirp,resulting from the self-steepening effect.As previously mentioned,chirped optical localized waves are of practical relevance to achieving pulse amplification or compression [18,23,24].

To search for exact chirped localized wave solutions of equation (1),we consider a complex traveling-wave solution of the form [18,25],

where the real amplitudeU(ξ)and phase modificationφ(ξ)are functions of the traveling coordinate ξ=x-vt,with v is the velocity of the traveling wave.Also,the parameter w represents the frequency of the wave oscillation.

Substitution of the expression of q(x,t)into the model(1)and separation of the real and imaginary parts yield coupled equations in U and φ as,

where the subscripts indicate partial derivatives.

Then,we can obtain an evolution equation for the phase modification φ(ξ) using equation (4) by multiplying it by the functionU(ξ)and integration as,

with A being an integration constant to be determined later.This result shows that dφ/dξ depends on U2,thus indicating that the phase of propagating waves possesses a nontrivial form which leads to the appearance of chirped nonlinear waves in the system.

The accompanying frequency chirp δω defined asδω=-∂ [φ(ξ) -ωt]∂xis given by

Scrutinizing the expression(6),we see that the frequency chirp property appears due to the self-steepening effect.One can also observe that chirp-free nonlinear waveforms may exist in the nonlinear medium in the case of vanishing selfsteepening (β →0) if we choose A=0.Importantly,this chirp includes two nonlinear contributions which are dependent on the wave intensity∣q(x,t)∣2=∣U(ξ)∣2.

Now,substituting equations (5) in (3),one obtains the ordinary nonlinear differential equation:

which describes the dynamics of the pulse amplitude in the non-Kerr quintic medium.Multiplying the amplitude equation(7)by the function dU/dξ and integrating once with respect to ξ,one gets

where B is the second integration constant.

We now make the transformation P=U2and write equation (8) as

where the coefficients a,b,c,and Ω are given by

With these results,we find that the general traveling wave solutions of the Gerdjikov–Ivanov equation(1)take the form,

withP(ξ)obeying the nonlinear differential equation (9) and φ(ξ)can be determined explicitly from equation(5).Also,the resultant frequency chirp across the propagating pulse is given by

Expression (11) describes various nonlinearly chirped traveling waves that may propagate in a non-Kerr quintic medium wherein the pulse evolution is governed by the Gerdjikov–Ivanov equation (1).These nonlinear waveforms can be generated from the closed-form solutions P(ξ) of equation (9) and the general waveform (11).It is worth pointing out that the case of localized waves on a zero background,which seems to be simple in the Gerdjikov–Ivanov equation case,has been extensively studied using various methods (see,e.g.[26–29]).In what follows,we study several types of localized pulses on a cw background for this model equation that are characterized by a nonlinear chirp.One should note that nonlinear waveforms appearing on a constant background are of practical interest in different physical systems including optical fibers,Bose–Einstein condensates and hydrodynamics,etc [31–33].

3.Chirped solitons on a cw background

We have obtained a variety of analytical soliton solutions on a cw background of model (1) which are characterized by a frequency chirp that is intensity dependent.

3.1.Bright solitons

We find an exact soliton solution for equation(9)of the form,

where λ,ρ and η are real parameters defined by

For this solution,the integration constants A and B are given by

If we insert these results into equation (11),one obtains an exact chirped soliton pulse solution for the Gerdjikov–Ivanov model (1) as,

with ξ0being an arbitrary constant.

Expressions (14) and (15) show that this localized wave exists when a>0,b<0 and 3b2>8ac.Moreover,from equation(16),we can see that the condition 16ac-5b2>0 is required for the constant A to be real.

The corresponding frequency chirp can be obtained readily as

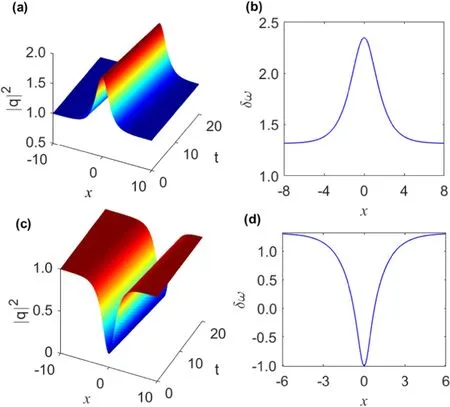
Figure 1.Evolution of intensity wave profile of the soliton solution (17) with parameters α=0.1,β=0.15,γ=0.08,v=-0.1,ω=-0.06125,v=-0.1,A=0.08,and ξ0=0(a)bright soliton on a cw background for the+sign and(b)dark soliton for the-sign.The corresponding chirp profiles for the (a) bright soliton and (b) dark soliton.

Figures 1(a)and(b)display the evolution of the intensity wave profile of the chirped soliton solution (17) with the lower sign and the upper sign,respectively.The adopted parameter values are: α=0.1,β=0.15,γ=0.08,v=-0.1,ω=-0.06125,v=-0.1,A=0.08,and ξ0=0.As seen,this solution represents a bright soliton pulse on a cw background for the upper sign and a dark soliton pulse for the lower sign.The profiles of accompanying frequency chirp for bright and dark solitons are exhibited in figures 1(c)and(d),respectively(for t=0).It is clear that the chirp for the bright pulse has a maximum at the center of the pulse,whereas for the dark pulse,it has a minimum;however,for both cases,it saturates at the same finite value as x →±∞.

3.2.Gray solitons

In what follows,we present the nonlinearly chirped gray soliton solutions of the Gerdjikov–Ivanov model (1) in two types.

(i) Type l

We obtained an analytical soliton solution for equation (9) as,

when the balance between the group velocity dispersion,quintic nonlinearity and self-steepening effect satisfies the relation

In this solution,the real parameters p,∊and r are related to the coefficients of the nonlinear differential equation (9) by

Then,by equating the parameters in equations (10) and (21),one obtains the following expressions of the wave velocity v,frequency w,and integration constants A and B:

It follows from expressions (24) and (25) that the integration constants A and B can be fixed easily with the pulse parameters p,∊and r,and consequently the physical meaning of these constants is very clear.Note that for the constant A in(24) to be real,we must require 0<∊<1.

By inserting these results into equation (11),one obtains an exact chirped soliton solution for the Gerdjikov–Ivanov model (1) as,

It should be remarked that this solution has three free parameters p,∊and r,and thus it describes a wide class of localized waves that are of great practical importance.Note that this soliton structure exists for the Gerdjikov–Ivanov model (1) with group velocity dispersion,fifth-order nonlinearity and self-steepening subject to the constraint condition(20).The latter condition shows the dispersion parameter α and the quintic parameter γ should be of the same sign(i.e.αγ>0),thus implying that the obtained nonlinearly chirped soliton can exist in anomalous (normal) dispersion for selfdefocusing (-focusing) nonlinearity.Naturally,the solution(26) reduces to a chirped dark-type solitonq(x,t)=±ptanh [r(x-vt-ξ0) exp [i(φ(ξ) -ωt)]for the case when ∊=1.

The frequency chirp associated with the chirped soliton(26) can be obtained readily as

Figure 2(a) shows the evolution of the intensity wave profile of the nonlinearly chirped soliton solution (26) for the material parameters α=0.25 and γ=0.2.To satisfy the existence condition(20),we set β=0.4.Also,the other soliton parameters are taken as p=1.6,∊=0.5,r=1,and ξ0=0.As concerns the pulse velocity v,it can be determined from equation (22) as v ≈-0.48.One can see from this figure that this solution represents a chirped gray pulse with a nonzero dip.The profile of the frequency chirp associated with this graytype solution is shown in figure 2(b)(for t=0).It is clear that this chirp has a minimum at the center of the pulse and saturates at the same finite value as x →±∞.

Figure 2.(a) Evolution of intensity wave profile of the gray soliton solution (26) with parameters α=0.25,β=0.4,γ=0.2,p=1.6,∊=0.5,r=1,ξ0=0 and (b) The corresponding chirp of the gray soliton solution.

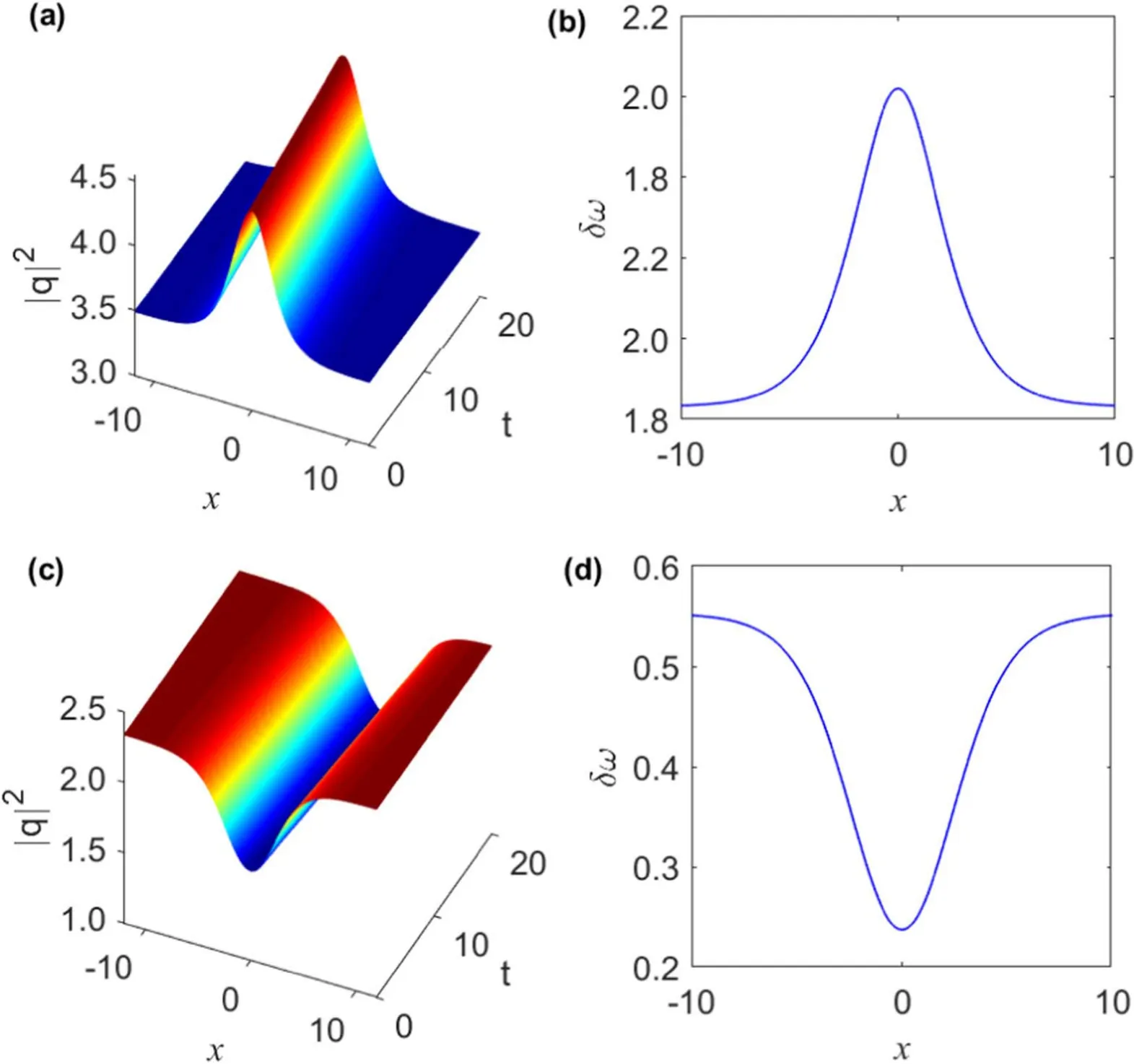
Figure 3.Evolution of intensity wave profile of the soliton solution(29)with parameters α=0.1,γ=0.08(a)bright soliton on a continuouswave background for Λ=0.3,β=0.15,v=-0.1 and (b) gray soliton with a nonzero dip for Λ=-0.3,β=0.18,v=0.1.The corresponding chirp profiles for the (a) bright soliton and (b) gray soliton.

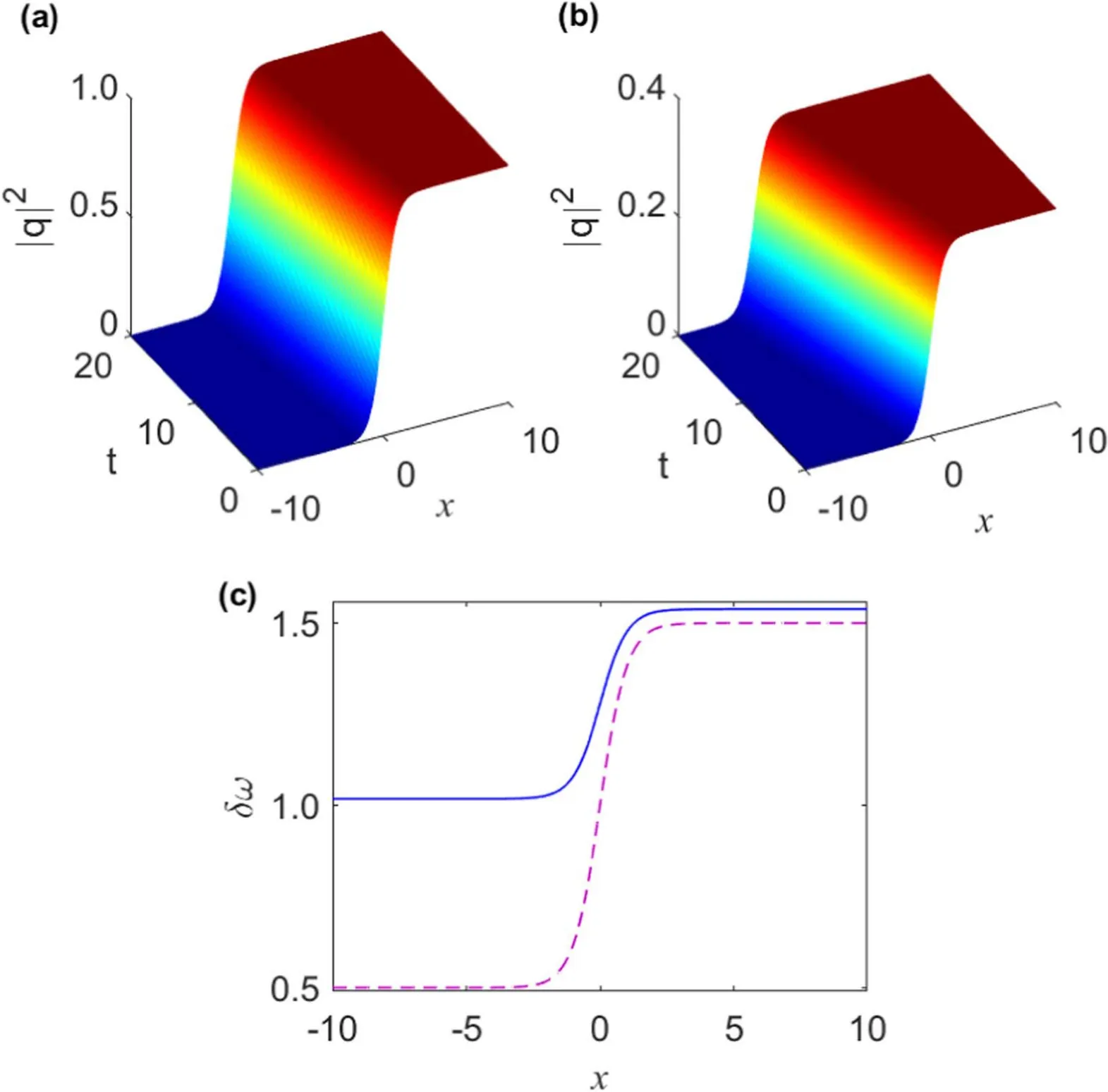
Figure 4.Evolution of intensity wave profile of the kink soliton solution (36) for different values of β (a) β=0.4 and (b) β=0.6.(c) The corresponding chirp profiles for β=0.4 (dashed line) and β=0.6 (thick line).The other parameters are mentioned in the text.

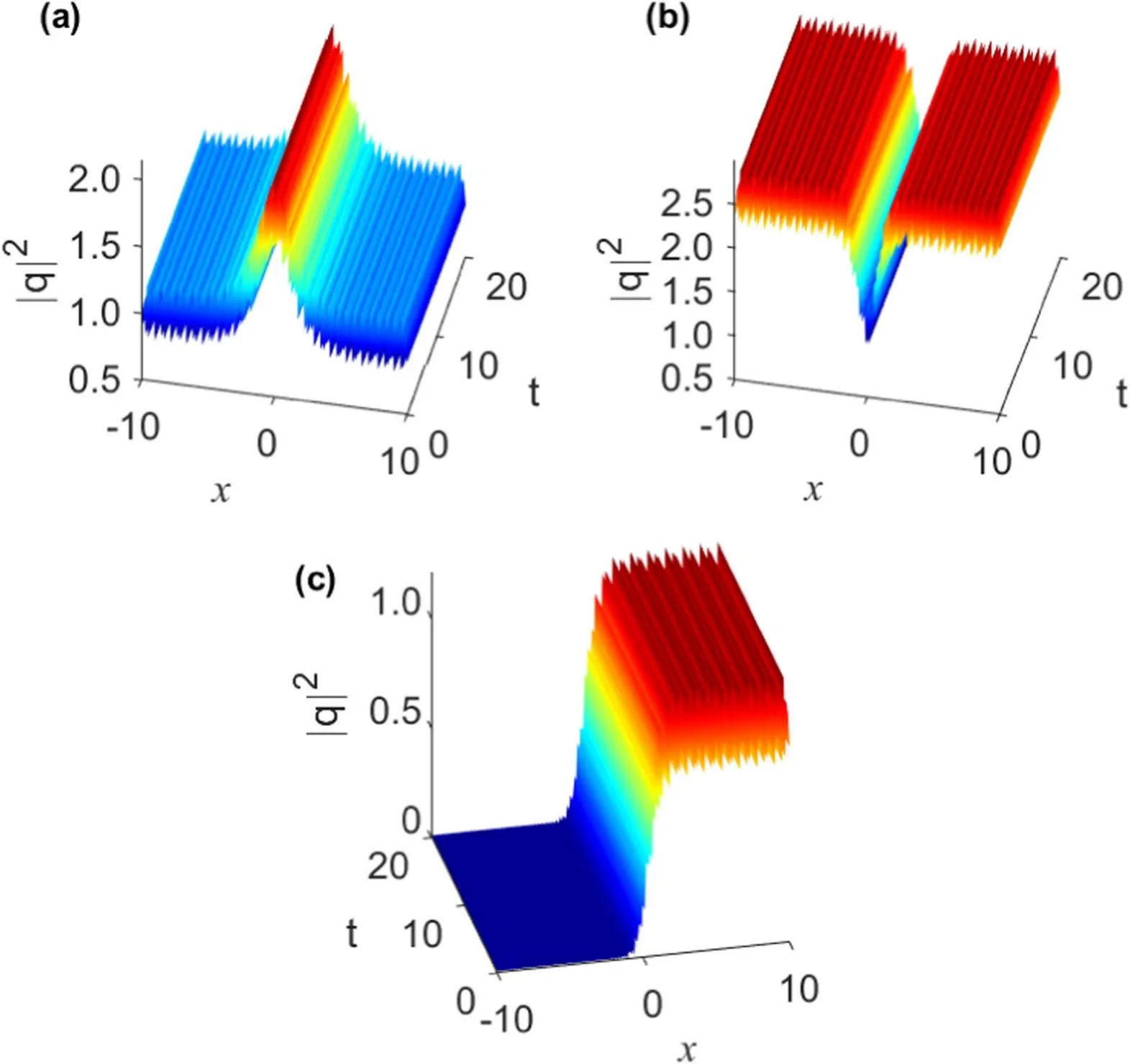
Figure 5.The numerical evolution of chirped(a)bright soliton solution(17),(b)gray soliton solution(26)and(c)kink soliton solution(36)under the perturbation with 10% initial white noise.The parameters are the same as those in figures 1(a),2(a) and 4(a),respectively.

(ii) Type 2

We find that equation (9) admits an exact closed-form soliton solution of the form,

which leads to a class of nonlinearly chirped solitary wave solutions for the Gerdjikov–Ivanov equation (1) as,

with Λ being a free constant which should satisfy Λ>-1.Note that for this chirped soliton solution,one finds that the first integration constant A vanishes while the second integration constant is equal to B=-μ2S2/16Λ,and the accompanying frequency chirp can be obtained readily as,

Physically,the expression (29) describes a nonlinearly chirped bright soliton on a cw background with an intensitytanh2[μ(x-vt-ξ0)]}for Λ>0 or a nonlinearly chirped gray soliton on a nonzero background and an intensity oftanh2[μ(x-vt-ξ0)]}for-1<Λ<0.As follows from equations(30)and(31),we see that the existence conditions of this chirped waveform are a>0,b<0 for Λ>0 and a<0,b>0 for -1<Λ<0.

The intensity profile of the chirped soliton (29) is depicted in figures 3(a) and (b) for α=0.1,γ=0.08 and different values of the free constant Λ,0.3 and -0.3,respectively.The other parameters are taken as β=0.15,v=-0.1 for the case when Λ=0.3 and β=0.18,v=0.1 for the case when Λ=-0.3.One can observe that the soliton(29) takes a bright waveform for Λ=0.3 and a gray waveform for Λ=-0.3.The profiles of associated frequency chirp (for t=0) are shown in figures 4(a) and (b),respectively.

3.3.Kink solitons

We have found the exact soliton solution of equation(9)to be

The real parameters R and h in this solution are defined by the expressions

under the constraint conditionsa<0 and c<0.

On substitution of the solution equations (34) into (11),we obtain a class of nonlinearly chirped soliton solution for the Gerdjikov–Ivanov equation (1) as,

Note that for this chirped solitary wave solution,we find that the integration constants A and B vanish and the associated frequency chirp reads,

The evolution of the intensity wave profile of kink soliton(36) is illustrated in figures 4(a)–(b) for α=0.1,γ=0.425,and different values of the self-steepening parameter β,0.4 and 0.6,respectively.Here the other parameters are taken as v=-0.1,ω=-0.125 for the case when β=0.4 and v=-0.2036,ω=-0.2036 for the case when β=0.6.These profiles show that the intensity of pulses decreases with the increase of the self-steepening parameter β.The chirp profile(for t=0)is shown in figure 4(c)for different values of β.It is seen from the figure that the amplitude of the frequency chirp can be controlled by varying this parameter.

From the above results,we can see that in the presence of the self-steepening effect,the Gerdjikov–Ivanov equation (1)supports different types of soliton structures on a cw background which exhibit a frequency chirping property.One notes that the novelty of the obtained nonlinear localized waves lies essentially in their functional shapes,which are different from the previously attained results.For example,we see that our chirped bright soliton solution (17) has a platform underneath it and involves a phase modification φ(ξ),markedly different from the soliton solution (3.7) presented in[29]which is unchirped and has a simple sech-type functional form.Moreover,the nonlinearly chirped soliton solutions(26),(29)and(36)obtained here for the Gerdjikov–Ivanov model are first presented in this paper.

4.Stability analysis

A distinctive property of localized waves is their stability to perturbations since only stable shape-preserving wave packets can be realized in experiments and utilized in practical applications.It is therefore important to investigate the stability of the derived nonlinearly chirped soliton solutions with respect to the finite initial perturbations.Here,we have performed a direct numerical simulation of model (1) using the split-step Fourier method [34] to verify the stability of solutions(17),(26)and(36)with initial white noise,as compared to figures 1(a),2(a) and 4(a).The evolution plots of chirped bright,gray and kink soliton solutions (17),(26) and (36)under the perturbation of 10% white noise are illustrated in figures 5(a),(b) and (c),respectively.The numerical results show that the chirped soliton structures remain stable after propagating a distance of twenty dispersion lengths.Hence we can conclude that the nonlinearly chirped soliton pulses we obtained are stable.

Finally,in order to strictly answer the question of stability of the chirped solitons presented here,we will use the stability criterion based on the theory of optical nonlinear dispersive waves [35,36] to analyze their stability analytically.We will also investigate the regimes for the modulation instability of a cw signal propagating inside the optical system by employing the standard linear stability analysis [37].Detailed stability analyses are now under investigation.

5.Conclusion

In conclusion,we have obtained the chirped soliton solutions on a cw background for the Gerdjikov–Ivanov model describing pulse evolution in a non-Kerr optical medium with higher-order effects such as self-steepening effect and quintic nonlinearity.The newly found chirped soliton solutions are essentially of the bright,gray and kink types and their accompanying frequency chirp is intensity dependent.The results show that the presence of the self-steepening effect contributes positively to create a nonlinearity in the pulse chirp for which the amplitude can readily be controlled through the change of the self-steepening parameter.We have also demonstrated the stability of the chirped solitons numerically with respect to finite perturbations of the additive white noise.The results showed that the obtained chirped structures can propagate stably under finite initial perturbations,such as white noise.Because of their exact nature,the localized pulses on a cw background obtained here may be profitably exploited in designing the optimal non-Kerr quintic optical material experiments.The present results report the first analytical demonstration of the existence of nonlinearly chirped solitons on a cw background obtained within the Gerdjikov–Ivanov equation framework.

Acknowledgments

Chun Wei is supported by the Ministry of Education’s Industry School Cooperation Collaborative Education Project of China under grant number 220405078262706.

Disclosures

The authors declare no conflicts of interest.