不同形状装药爆炸作用下地下管廊动力响应研究*

谢玖颐,李书进,陈志华

(武汉理工大学 土木工程与建筑学院,武汉 430070)

城市地下综合管廊是城市地下用于集中敷设电力、通信、广播电视、给水、排水、热力、燃气等市政管线的公共隧道,是城市的“生命线”,近年来成为研究热点。它能够高效保障城市运转,但在未来战争中也可能是打击重点。其规模庞大暴露明显,埋深一般较浅且易损性强,很难承受精确制导武器打击。一旦关键部位、薄弱部位遭受致命打击,将导致大面积破坏,内部管线损毁严重,传输功能丧失。因此管廊对于战时的重要性不言而喻,管廊结构应具备抵抗预定等级常规武器爆炸荷载破坏的能力。要确保管廊结构的防护能力,首先需要较准确地确定施加于管廊结构上的爆炸作用。

对于地下结构的爆炸模拟,许多学者通过大量研究并取得了一定的成果。霍庆等探究了地下拱形结构在侧顶爆炸作用下的破坏模式以及影响因素[1]。王超申等对地下巷道结构进行爆炸模拟,探究了不同分配层的削波能力[2]。杜修力等利用LS-DYNA和粘弹性人工边界条件建立了爆腔、地下结构、软回填隔震层和岩石介质系统三维粘弹塑性动力响应分析模型[3],探究了软回填层的隔震效果。谢乐等对地下矩形截面通道在土中爆炸荷载作用下的响应进行了数值模拟[4],探究了结构顶部加压后的变化。范余俊等[5]、张茜研究了炸药在地面爆炸的条件下[6],土中浅埋结构地冲击荷载作用特点以及土中冲击波的传播规律。江水德等分析了地面爆炸土中浅埋钢筋混凝土箱型结构的破坏特征和动力响应[7],得到了结构顶板厚度和侧墙厚度适宜比。邓鹏[8]、宋海贤研究了地下结构在内部爆炸作用下内部构件动力响应以及灾变响应[9]。邓贵德等运用数值模拟的方法分析了球形和圆柱形装药中心起爆情况下的土中近场爆炸载荷[10],探究了不同装药形状爆炸冲击波在土中传播规律的区别。郑云木等研究了柱状装药和集团装药在岩体中爆炸时[11,12],对地下拱形结构响应的区别;并探究了柱状装药在不同位置爆炸时结构损毁情况,提出引入装药爆炸位置影响系数,量化了爆炸位置因素对结构损毁的影响程度。

常规武器的工程防护研究,过去更多关注的是结构本身的破坏效应,许多工程设计只对结构的强度和抗力进行了校核,却没有考虑结构内部的振动效应带来的破坏。研究表明,在强烈爆炸冲击下,恶劣的振动环境是人员伤亡、设备失效的主要原因,且地震作用对其内部振动响应远小于爆炸作用[13]。对于地面爆炸、岩土内爆炸作用下地下管廊响应,多采用集团装药进行模拟,没有考虑装药形状对土内爆炸作用下管廊结构的影响。在实战中,大量使用的精确制导炸弹可视为柱状装药,而其在近区的爆炸效应和集团装药有着明显区别。通过模拟炸药在土内爆炸时管廊结构动力响应,讨论不同装药形状下的结构响应变化规律,得到一些对工程有意义的结论。

1 数值模型

综合管廊有多种形式,单舱管廊分为综合舱、缆线舱、高压电力舱、管道舱、热力舱、天然气舱等,内部放置了给水管、热力管道、通信线缆等设施;双舱管廊有两个舱位,可以针对不同需要,将不同类型的单舱进行组合,如图1所示。对于双舱管廊受到不同装药形状下土内爆炸的动力响应研究,还未见相关研究报道。以某双舱地下综合管廊为例,对不同形状装药爆炸下结构动力响应进行研究。其中,不同装药形状,即采取柱状装药与集团装药两种形式。

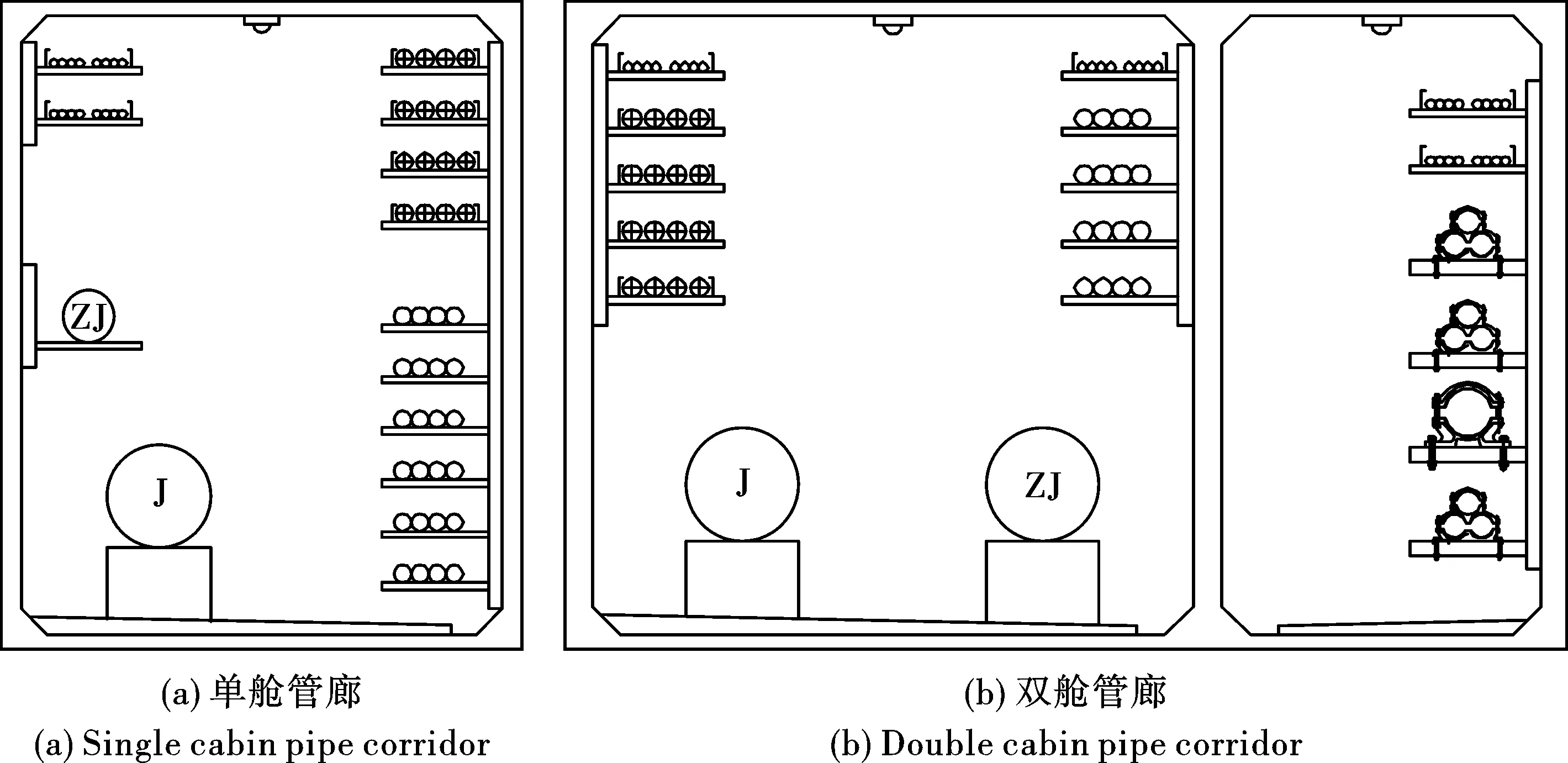
图1 综合管廊断面图Fig. 1 Cross section of comprehensive pipe corridor

1.1 几何模型

整体模型采用空气、土、钢筋、混凝土、炸药五种材料组成。结构外边长总尺寸为675 cm×390 cm×1400 cm。管廊分为大小两舱,大舱净宽度360 cm,小舱净宽度210 cm,舱内净高度300 cm,上下方顶板厚度均为40 cm,左右两侧承载墙厚度为40 cm,中间隔墙厚度为25 cm。在顶板、底板、外墙以及隔墙均布置了受力筋、分布筋以及拉结筋。管廊内部附属设施通过施加集中质量进行模拟,不考虑其刚度。管廊总长度为1400 cm,在其顶部覆土层厚度为500 cm。炸药设置在管廊顶部中心处,炸药等效TNT当量117.5 kg,采用中心起爆,爆心距离结构顶板300 cm,炸药和管廊周围的土简化为各向同性的均匀土体。设沿着管廊675cm边长方向为X向,沿着管廊380 cm边长方向为Y向,沿着管廊1400 cm边长方向为Z向。假定炸弹等效为直径23 cm,高度135 cm的柱状装药;等量集团装药长宽高均41 cm,装药量以及爆心位置均相同。模型XY断面如图2所示。

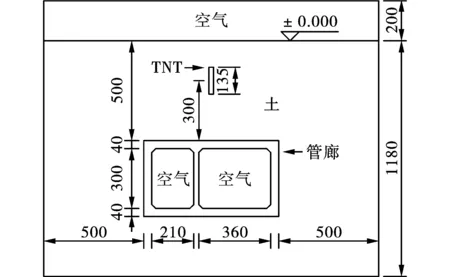
图2 数值模型简图(单位:cm)Fig. 2 Numerical model diagram(unit:cm)

1.2 算法及边界条件

模型中的空气、土、混凝土、炸药均采用SOLID164单元,钢筋采用LINK160,统一采用cm-g-μs单位制。结构离左右边界均为500 cm,距离底边界300 cm。钢筋和混凝土采用分离式模型,不考虑钢筋和混凝土之间的滑移。由于涉及空气、土、炸药等大变形,在爆炸荷载作用下管廊响应分析中。空气、土、炸药、结构间的作用使用流固耦合算法。空气、土、炸药采用Euler网格进行划分,管廊结构采用Lagrange网格划分,避免了因为网格畸变过大造成的计算不收敛。模型中,炸药采用高爆炸药材料和JWL状态方程描述,炸药周围为土和空气单元,爆炸后,炸药产物在空气和土网格内流动。

土介质和结构之间定义自动面面接触。土壤底面和侧面采用无反射边界模拟半无限空间,减小边界反射造成的计算误差。考虑管廊对称性并节省计算时间,建立一半的模型,并以沿管廊纵向的爆炸中心截面作为对称面。有限元模型如图3所示。

图3 地下管廊爆炸有限元模型Fig. 3 Finite element model of underground pipe corridor explosion

1.3 材料模型

计算模型中空气采用*MAT_NULL材料模型和状态方程*EOS_LINEAR_POLYNOMIAL进行描述。土介质模型采用带失效的*MAT_SOIL_AND_FOAM的模型模拟。炸药采取*MAT_HIGH_EXPLOSIVE_BURN材料模型和*EOS_JWL状态方程描述。混凝土材料采用*MAT_JOHNSON_HOLMQUIST_CONCRETE模拟,该模型可以模拟混凝土在高压、高应变率、大变形等情况下的应力应变关系[14]。钢筋采用的*MAT_PLASTIC_KINEMATIC模型,这是一种与应变率相关和带有失效的弹塑性材料模型。应力应变关系近似地用两条直线表示,应变率效应用Cowper-Symonds模型描述。具体参数如参考文献[14]、[15]。

1.4 结果验证

根据美国TM5-855-1手册中侧爆加载情况下矩形埋设结构的经验公式求得自由场平均加速度[16],然后用该值乘以折减系数来求得结构内部的平均加速度。对于顶爆情况同样适用。将数值方法计算所得的结果和TM5-855-1手册中爆炸作用下矩形埋设结构的经验公式预估值进行比较,以验证数值模拟的有效性。

(1)

P0=48.77f(ρc)(2.78R/W1/3)-n

(2)

式中:Aavg为结构所在处平均自由场的加速度,g;R1、R2分别为爆心至迎爆面与背爆面的距离,ft;W为炸药当量,lb;n为衰减系数;c为地震波波速,ft/s;f是耦合系数,对于土中埋地爆炸,f=0.45;P0为峰值压力,Pa;ρc为岩土介质波阻抗(kg/m2s);W为炸药当量,kg;R为爆心距,m。参考文献[13]及TM5-855-1,取c=400 m/s,n=2.8,W=259 lb。

以集团装药模拟结果为例,本文数值模拟求得的平均响应峰值可以近似取为迎爆面中点和背爆面中点的平均值。对于结构加速度,经验公式算得1017.81 m/s2;数值模拟结果为959.64 m/s2,误差5.7%。沿着爆心轴向取8个点,通过经验公式计算土压力与数值模拟相应点的结果进行比较,如图4所示。其中比例距离Z=d/W1/3,d为炸药爆心距,m;W为炸药当量,kg。

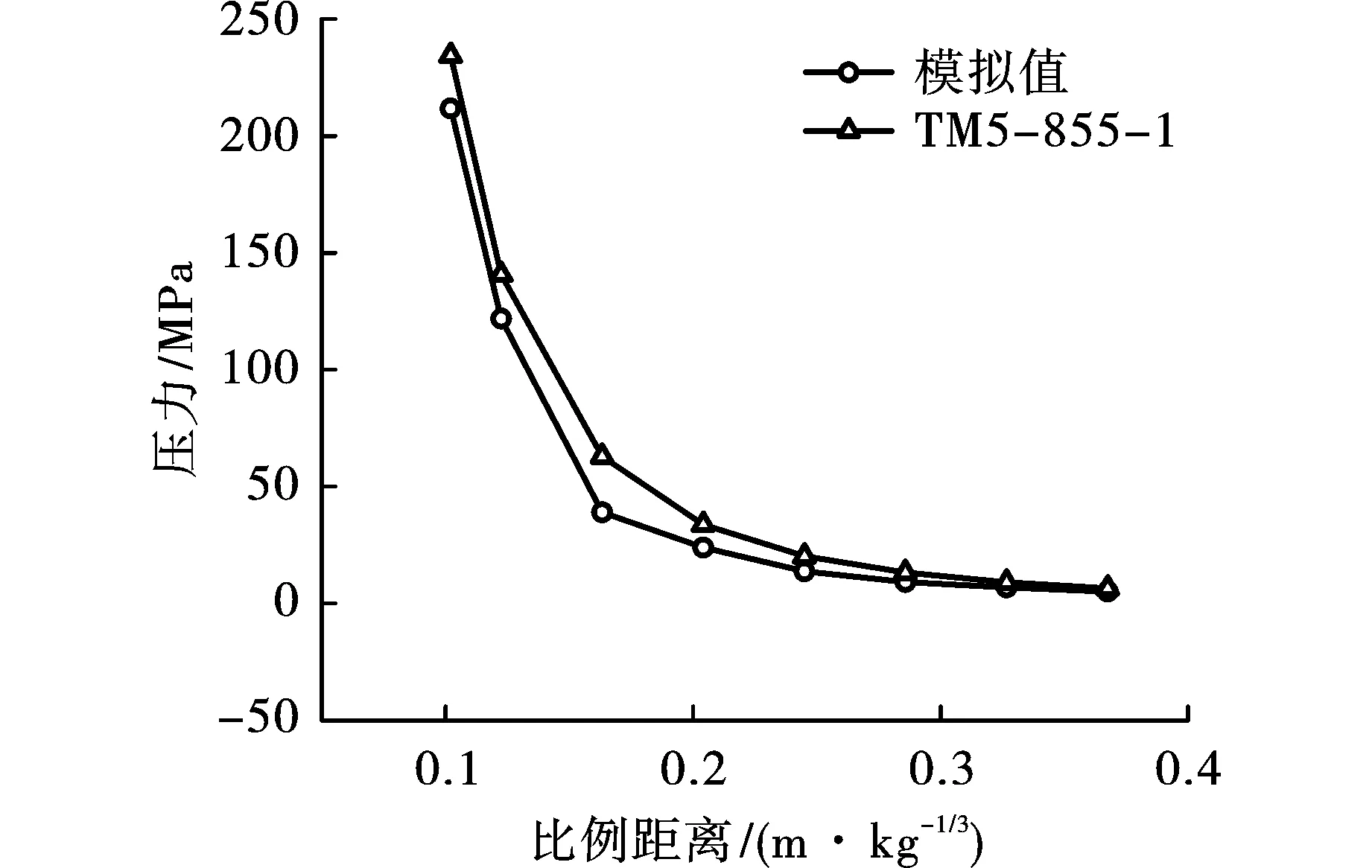
图4 数值模拟方法与TM5-855-1计算结果对比图Fig. 4 Comparison between the numerical simulation and TM5-855-1

由图可见,数值模拟土压力结果与经验公式计算结果基本符合,在比例距离较小的情况下有所误差,随着比例距离增大,其误差越来越小。产生误差的原因可能是土介质在动荷载作用下的特性多变。以上说明本文数值模拟的计算模型简化假定以及材料模型参数选取是合理的。

2 柱状装药与集团装药爆炸响应分析

2.1 冲击波传播规律

炸药在土内爆炸冲击波的形成过程以及随着时间的传播情况,如图5～7所示。由于结构变形较小,空气压力产生影响甚微,仅将结构和土中应力波作为研究对象。可见,冲击波传递到结构之前,柱状装药冲击波波阵面呈椭圆形,且椭圆长轴与柱状装药的长轴方向一致;集团装药冲击波波阵面呈球形,以球面波向各个方向传播,爆炸荷载不存在明显的方向性。在5 ms时冲击波已经到达结构内部,而集团装药冲击波刚传至顶板。可见柱状装药爆炸后在土内产生的应力波沿轴向传播的速度大于集团装药。冲击波遇到结构后产生复杂的入射、反射效应。在10 ms时两种装药的冲击波传播范围相似,冲击波到达结构顶板,开始同时向外墙以及隔墙传播。随后冲击波在结构内部反复传播,随着时间的推移和传播距离增加,爆炸压力充满整个土边界内部空间。

图5 1 ms时的冲击波压力云图Fig. 5 Shock wave pressure nephogram at 1 ms

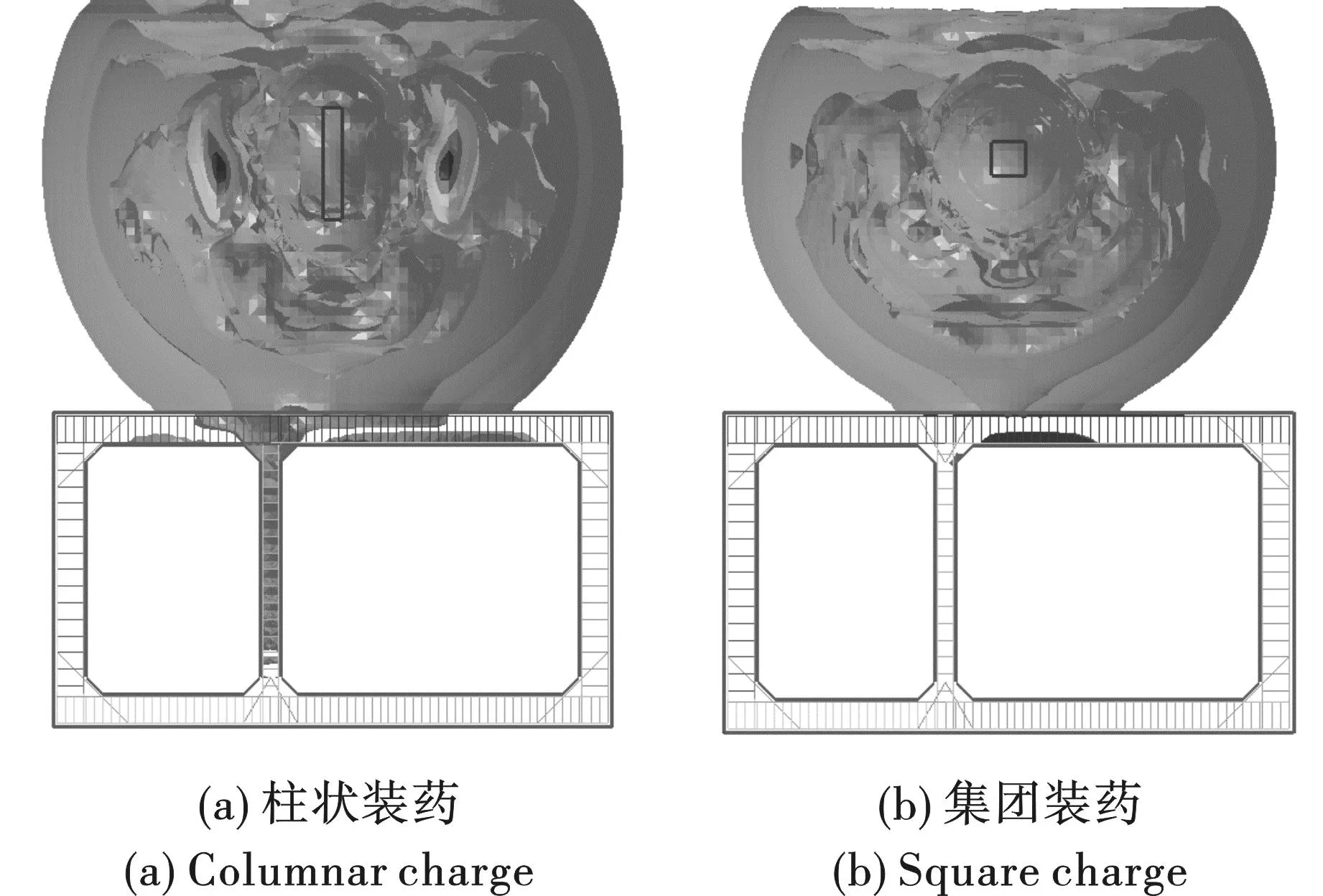
图6 5 ms时的冲击波压力云图Fig. 6 Shock wave pressure nephogram at 5 ms

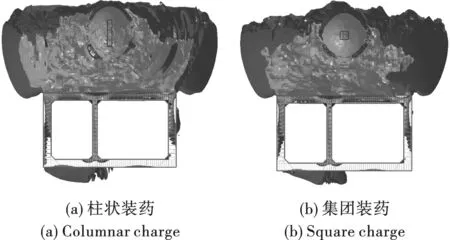
图7 10 ms时的冲击波压力云图Fig. 7 Shock wave pressure nephogram at 10 ms

图8为柱状装药和集团装药爆炸时冲击波超压峰值随着比例距离的分布。由于集团装药爆炸冲击波呈球状,无明显方向性,在此仅取沿轴向位置单元的超压值。图8表明,在比例距离小于0.5 m/kg1/3时,柱状装药的径向和轴向超压明显不等,相同比例距离的轴向超压大于径向超压,且峰值的差异在比例距离小于0.2内尤为明显,随着比例距离的增大,二者差异逐渐减小。柱状装药的轴向超压大于相同比例距离集团装药的轴向超压,前者峰值约为后者峰值的1.12～4.79倍。在比例距离小于0.4 m/kg1/3时,柱状装药径向超压峰值甚至大于相同比例距离的集团装药轴向超压峰值。该结论与文献[10]中的结论一致。由此可见,柱状装药爆炸产生的爆炸波存在明显的方向性,爆炸波沿着装药轴向传播的速度和超压峰值均大于相同当量集团装药。

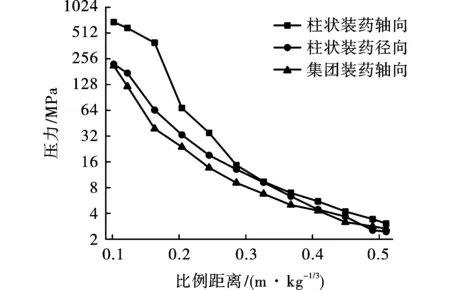
图8 两种装药情况下的超压峰值分布Fig. 8 Peak pressure distribution under two charges

2.2 振动加速度对比分析

在结构运动参数较大的位置选取监测单元,对结构局部进行分析。所选单元的具体位置如图9。

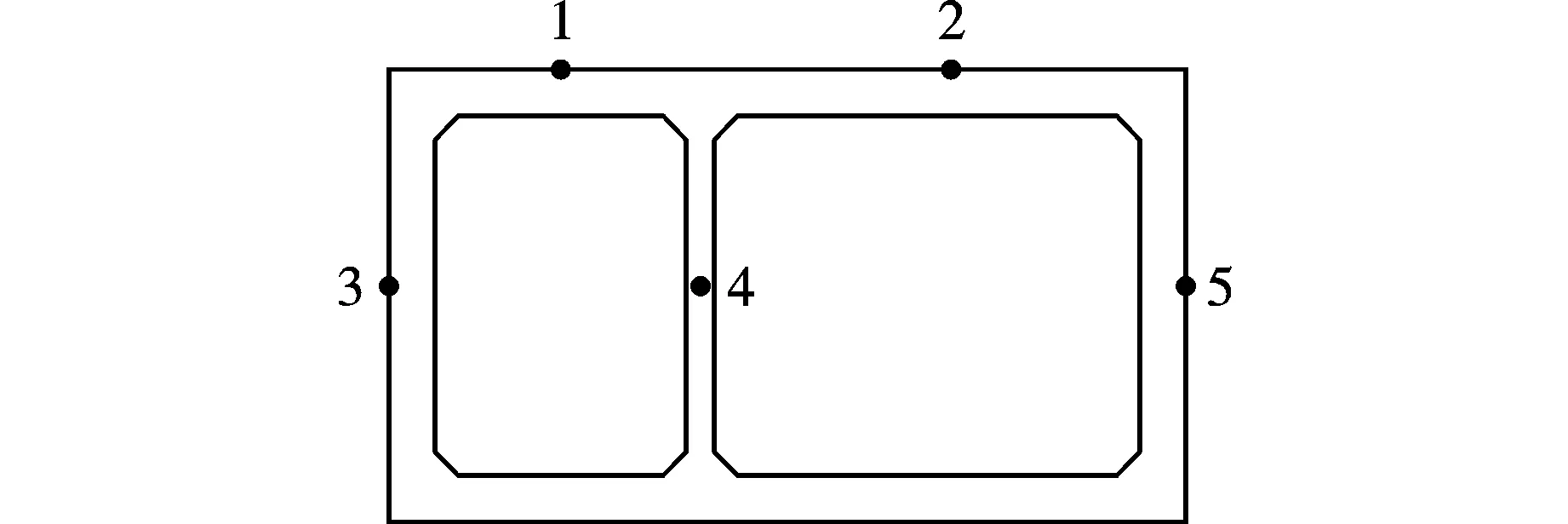
图9 监测单元布置图Fig. 9 Location of monitoring units

对于不同的构件,根据其构造特性分析不同方向上的加速度。对于结构顶板,主要分析其竖向加速度;对于侧墙和隔墙,主要分析其水平加速度。图10为单元2位置的Y向加速度时程曲线以及单元4位置的X向加速度时程曲线,表1给出了各单元峰值对比。从图中可以看出,在爆炸初期,爆炸应力波还未传递到结构上时,结构的加速度几乎为零。在柱状装药情况下,爆炸开始后4 ms左右,单元2最先达到加速度峰值,为2196 m/s2,随后单元1也达到了加速度峰值。在单元1、2竖向加速度到达峰值时,单元3、4、5的竖向加速度几乎为零。结构侧墙的竖向加速度响应并不明显。在两种装药形状下,各单元加速度曲线的波形相似。集团装药爆炸时单元1、2到达加速度峰值的时间慢于柱状装药爆炸情况,约为5 ms。在单元1、2到达峰值后的波动幅度也不如柱状装药爆炸时该处单元的振幅。柱状装药爆炸下的顶板竖向加速度峰值高于集团装药。大舱顶板部位高出15.6%,小舱顶板部位高出12.2%。对于侧墙部位的竖向加速度影响并不是很大,因此取隔墙水平向加速度进行比较。可见,两种装药形状下水平向加速度波形几乎一致,仅峰值稍有差别。这是由于柱状装药爆炸时的爆炸波呈现出明显的方向性,波形为空间十字形分布,沿着轴向的传播速度快于沿着径向的传播速度。而集团装药爆炸时爆炸波的形状为球形,其沿着轴向的爆炸波传播速度和强度都不如柱状装药爆炸时的情况。因此主要体现在竖向响应的不同。

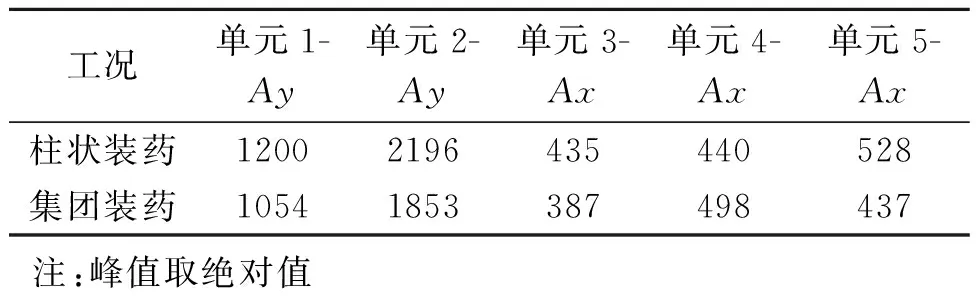
表1 各单元加速度峰值对比表(单位:m/s2)Table 1 Comparison table of acceleration peak value(unit:m/s2)

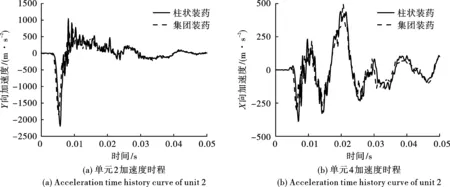
图10 加速度时程曲线Fig. 10 Acceleration time history curve

2.3 振动位移对比分析

图11为两种装药形式爆炸下结构顶板Y向位移时程曲线。可见,结构在柱状炸药爆炸作用下,顶板的位移从爆炸后5 ms开始逐渐增大,在40 ms时趋于稳定。单元1、2增大到峰值后发生回弹,最后趋于稳定,且单元2的回弹幅度明显大于单元1,表明结构大舱顶部变形幅度大于小舱顶部。当单元2到达位移峰值时,单元1的位移数值还在处于增大状态。两种装药形状下结构顶部位移曲线变化趋势相似,只是峰值到达时刻和峰值有差别。集团装药情况下各单元位移从爆炸后6 ms开始逐渐增大,在40 ms时各单元趋于稳定,约为0.01 m。柱状装药各单元在40 ms时趋于稳定,约为0.012 m。

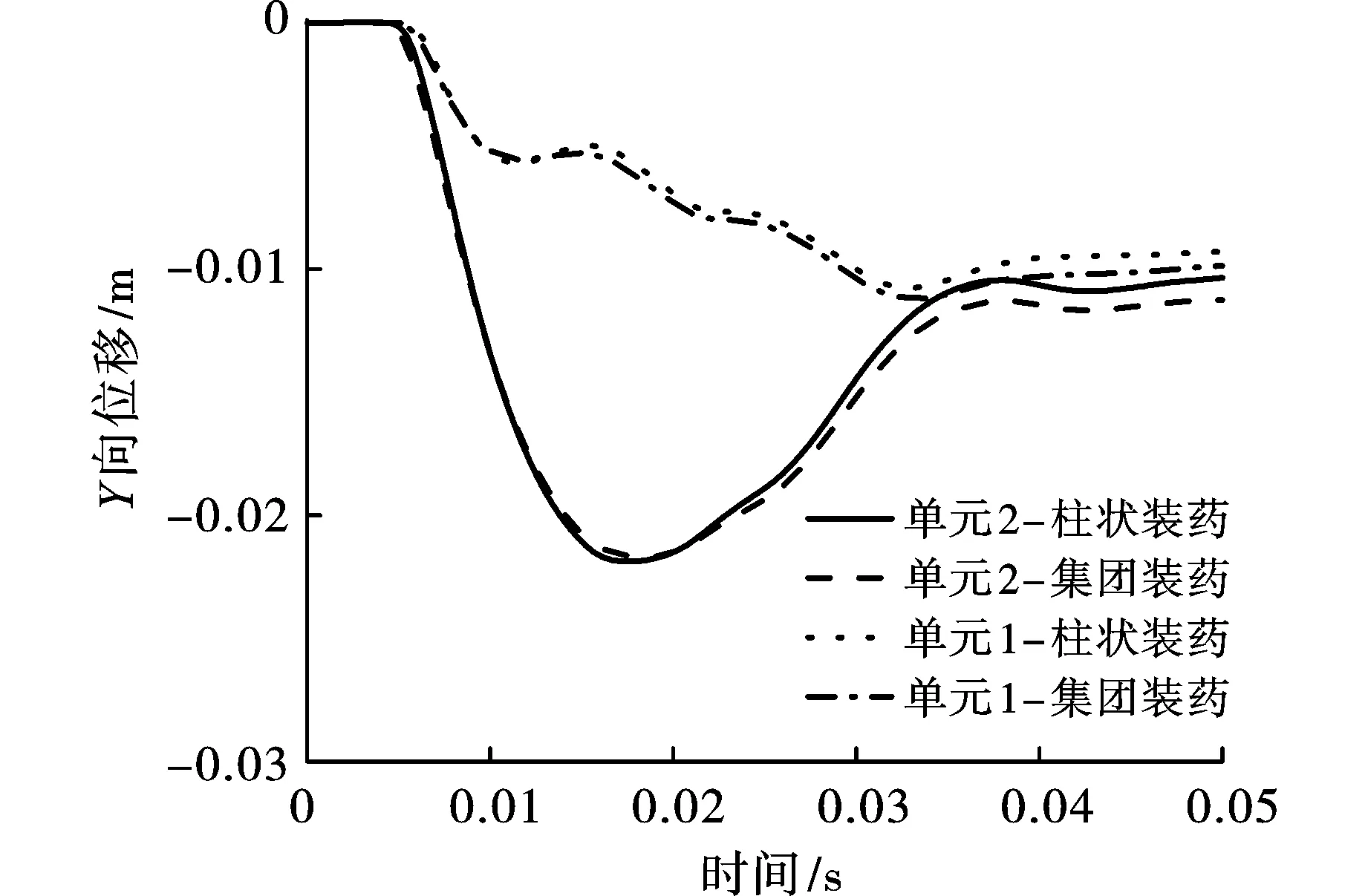
图11 结构顶部Y向位移时程曲线Fig. 11 Time history curve of Y-direction displacement at the top of the structure

3 结论

(1)在两种装药顶爆作用下,主要是结构顶部竖向响应的区别。在比例距离小于0.5 m/kg1/3时,柱状装药在相同比例距离的轴向超压大于径向超压,前者峰值约为后者峰值的1.12～4.79倍。在比例距离小于0.4 m/kg1/3时,柱状装药径向超压大于同比例距离集团装药的轴向超压。爆炸产生的土中应力波沿装药轴向传播速度大于径向传播。

(2)柱状装药爆炸下的顶板竖向加速度峰值高于集团装药。大舱顶板部位高出15.6%,小舱顶板部位高出12.2%。两种装药形状下结构顶部位移曲线变化趋势相似,只是峰值到达时刻和峰值有差别。由于结构顶部到爆心的比例距离超过0.5 m/kg1/3,该处柱状炸药爆炸冲击波径向压力与集团炸药已经差别不大,因此结构侧墙以及隔墙水平向的响应区别较小。

(3)战时导弹大多数为柱状,使用集团装药进行模拟,可能导致防护安全性偏低。工程防护设计中需要考虑装药形状的影响,以确保安全可靠。