面向月面大范围移动任务的脱困方法研究

王雨政，崔宇新，王慎泉，柏合民，张崇峰，王卫军*

（1.上海宇航系统工程研究所，上海 201109； 2.北京航空航天大学，北京 100191；3.上海航天技术研究院，上海 201109； 4.中国航天员科研训练中心，北京 100094）

1 引言

月球探测任务是人类太空探索的重要组成部分，随着探测任务的不断深入和扩展，对探测范围与能力有了更高的要求，具备千公里级连续移动能力和吨级载荷运输能力的月面大型移动平台逐渐成为研究热点，是未来月球探测的关键装备之一［1-3］。

月面大范围移动面临极大风险，月面环境恶劣，地形复杂，地表覆盖有厚度不等的松散月壤，承压能力低，移动平台的通过能力难以覆盖全月面地形［4-5］，此外，受限于导航、制导与控制（Guidance、Navigation and Control，GNC）技术的不足，月面快速可靠的路径规划与风险区域规避难以实现［6-8］。千公里级大范围移动跨月面地质带，移动平台极有可能在行驶过程中因沉陷、落坑、车轮卡滞等因素失去移动能力而面临受困的风险，不仅限制了任务的实施和推进，同时给移动平台的安全性带来极大挑战，对月面重大资产的保护能力提出了极高的要求。因此，研究月面大型移动平台的脱困技术，对于提高其机动性能，促进任务的顺利执行具有重要的现实意义和应用价值。

目前，关于月面大型移动平台脱困问题的研究十分有限，研究工作主要集中在地球上的车辆脱困或星表小型巡视器脱困。对于地面车辆，常用的脱困方法包括利用拖车绳借助外力将被困车辆牵引脱困，在轮上附加防滑链等辅助装置以改善轮地附着性能脱困，在地面铺设临时路面增大支承能力脱困，利用主动悬架改变车轮与地面之间的相对位置脱困等［9-10］；对于星表小型巡视器，高海波等［11］提出了一种利用摇臂式主动悬架使车轮抬离地面以脱离沉陷的脱困策略，此外还有采用可变形或特殊构型车轮以适应不同地形条件以及采用轮腿复合等特殊行走机构提高机动能力从而实现脱困的方法［12-13］。然而，月球的环境条件与地球有显著差异，大型移动平台也不具备小型机器人灵活的移动构型，这些研究成果在月面大范围移动任务中的实际应用价值还有待进一步研究。

移动平台可采用的移动构型种类较多，目前星表巡视器以轮式构型最为成熟，本文针对月面大型轮式移动平台脱困技术展开研究。首先，对月面大范围移动任务中可能面临的典型受困工况进行分析，确定可致受困的临界地形参数；然后，结合月面环境特点和大型移动平台移动任务需求，提出并设计采用脱困机器人锚定，并进行牵引脱困的总体方案；最后，对该方案所需牵引力及牵引角度进行计算分析，并通过动力学仿真对分析结果进行验证。

2 月面受困工况分析

在月面进行大范围移动是一项具有高度不确定性的任务，实际移动过程中可能出现多种不同的受困工况。根据对月面的探测数据与现有资料，结合月面环境的特殊性对月面大范围移动过程中可能面临的受困工况进行初步分析，并计算临界受困地形参数。

2.1 疏松月壤区域沉陷

月表覆盖有厚度不同、密度不等的月壤，不同地区月壤的承压能力也存在差异。苏联月球车一号在月面共行驶10 540m，其行驶路线上的月壤承载能力大多在20 ～100 kPa 范围内波动，但同时也存在少数承载能力不足5 kPa 的极端疏松区域［14］；美国阿波罗11 号航天员月面行走时鞋底平均压强约7 kPa，在疏松月壤区域的脚印深度可达150 ～200 mm［15］。由于移动路径上的月壤承载能力数据难以提前获得，在执行大范围移动任务时，将有可能驶入疏松月壤区发生沉陷受困。移动速度较缓慢时，如部分车轮发生沉陷可及时发现进而停止移动，但当高速移动时可能无法及时响应，进一步驶入疏松区域导致整车沉陷。

为方便分析，做出以下假设：车轮不发生形变，且左右对称，受困状态一致。对整体沉陷受困工况进行建模分析，在该工况下，车轮下半部分陷入地面，临界脱困状态时，每个车轮仅在地表高度处与地面接触，移动平台受力情况如图1 所示。

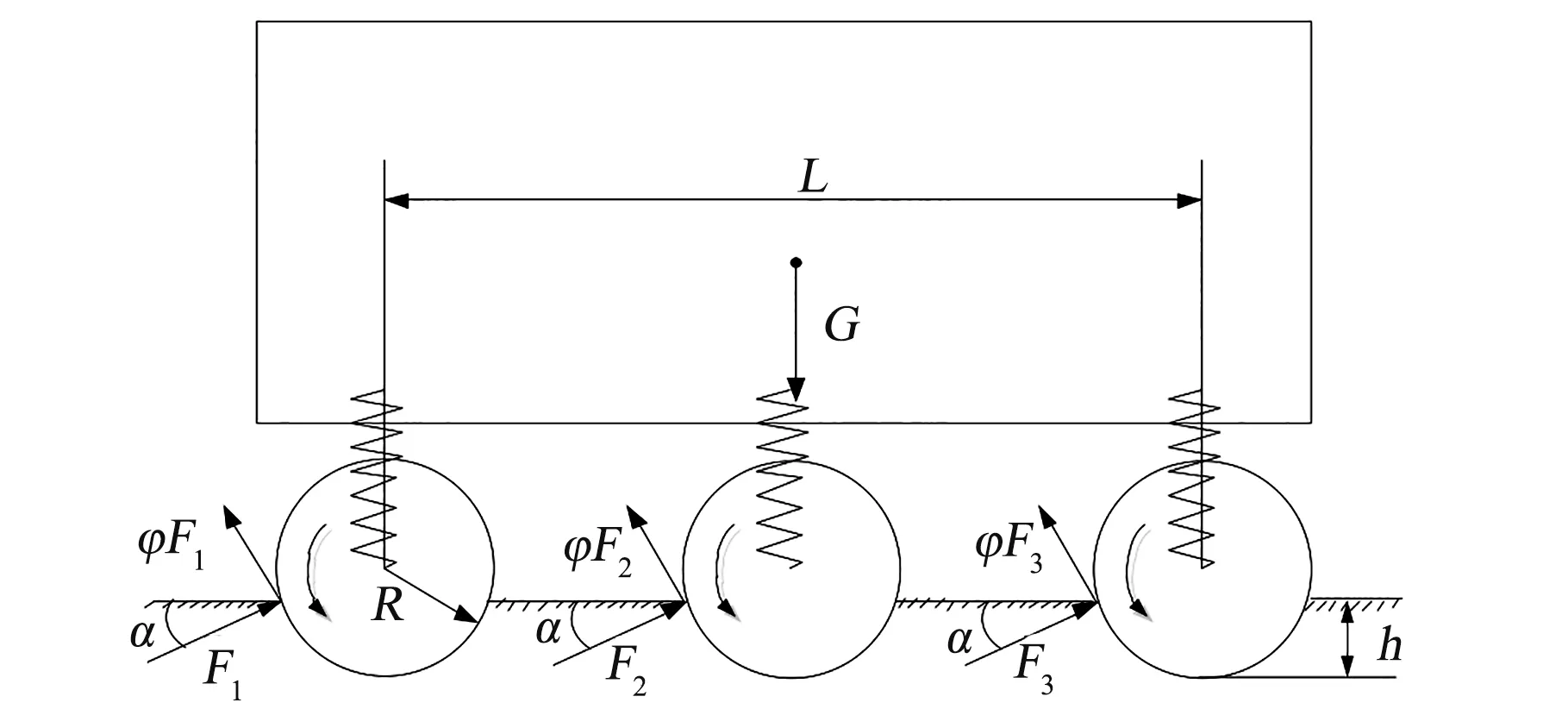
图1 整体沉陷受困模型Fig.1 Model of overall subsidence trapping

图中，F1、F2、F3分别为地面对前、中、后轮的支持力，α为支持力方向与水平方向的夹角，φ为轮地附着系数，G为大型移动平台重力，h为沉陷深度，R为车轮半径。假设质心和中轮水平方向位置均在移动平台中点，对移动平台临界状态受力情况列出方程组，见式（1）。

求解该方程组得式（2）。

此即为沉陷临界深度，当沉陷量超过该数值，大型移动平台则会发生受困。

2.2 障碍卡滞受困

月面广泛分布有不同尺寸的岩石和沟谷，大范围移动过程中将不断经过各种障碍，虽然导航系统会帮助规避无法越过的障碍，但难以保证准确及时地全部识别，大型移动平台可能会由于车轮被卡滞而受困，也有可能因为部分移动系统故障导致越障能力降低而受困。障碍受困模型如图2 所示。

图2 障碍受困模型Fig.2 Model of obstacle trapping

图中，α为前轮支持力方向与水平方向的夹角，h为障碍高度。假设移动平台未发生倾斜，则每个轮竖直方向受力相等，对移动平台临界状态受力情况列出方程组，见式（3）。

求解该方程组得式（4）。

此即为临界越障高度，当障碍物高度超过该数值，大型移动平台则无法越过而受困。

2.3 大坡度地形受困

月面大部分区域坡度在0°～23°之间，部分极端区域可能会超过这个范围，如高地地区最大坡度约为34°，撞击坑内侧坡度在25°～50°之间［16］。由于爬坡性能要求与移动系统的质量代价紧密相关，月面移动平台的爬坡能力通常在20°～30°之间以满足绝大多数月面行驶工况，但因为存在超过此区间的大坡度地区，在大范围移动时仍有可能面临坡面受困的风险。

当月面移动平台行驶在大坡度地区时，可能会由于质心在竖直方向的投影超过车轮的支撑包络范围而发生侧翻，也有可能由于坡面使得重力在垂直于坡面方向的分量减少，轮地接触压力下降进而导致牵引力不足，车轮打滑无法移动。此外，在大坡度地区往往会伴随出现厚度较大的疏松月壤，增大爬坡难度，且大概率出现坡面沉陷而受困。坡面受困模型如图3 所示。

图3 坡面受困模型Fig.3 Model of slope trapping

图中，α为坡面与水平面的夹角，a为质心高度，L为前后轴轴距，对移动平台临界状态受力情况列出方程组，见式（5）。

对该方程组进行消元并求解，可解得临界爬坡角度，见式（6）。

从该结果可知，此方法计算出的临界爬坡角度仅与轮地附着系数有关。当质心竖直方向在地面的投影超过车轮的包络范围时，移动平台将发生倾覆，计算此时坡面与水平方向夹角，见式（7）。

综上，大型移动平台坡面受困的临界角度即为以上两结果中的较小值，见式（8）。

当坡度超过该数值，大型移动平台将无法继续行驶而受困。

3 脱困方案设计

为确保月面大型移动平台脱困的可靠性，脱困成功率和多工况的适应性是脱困方案设计的关键考虑因素，方案应能够实现疏松月壤沉陷、崎岖路面卡滞、大坡度等多种受困场景的脱困目标；另外由于航天发射质量成本高，质量资源占用也需要重点考虑，脱困设备的质量应控制在大型移动平台总质量的0.05 倍以下，且需要具备重复使用能力；此外，由于大型移动平台在月面环境下工作，并且长时间运行在无人值守的工作模式，脱困工作应具备高度自动化能力，能够在没有航天员和其他载具参与的情况下，接收地面的遥控指令完成脱困全流程。

鉴于现有脱困技术积累，本文提出一种基于脱困机器人锚定并牵引的脱困方案。脱困机器人携带锚定设备移动至指定位置进行稳固锚定，随后牵引大型移动平台脱离受困区域。此外，当大型移动平台出现零部件损坏时，脱困机器人可辅助进行设备维修和更换操作，在进行月面考察任务时，脱困机器人也可作为小型移动探测器，利用自身较强的地形通过能力以及可以与大型移动平台相互连接配合的特点，进行溶洞、撞击坑等特殊地形的探测，实现功能复用。

3.1 脱困机器人构型

脱困方案所采用的脱困机器人基本构型如图4 所示，包含移动模块、锚定模块、牵引模块、操作模块和测控通信模块。

图4 脱困机器人基本构型Fig.4 Basic configuration of the recovery robot

脱困机器人整体质量约300 kg，采用六足式移动构型和大承载足垫，能够有效应对疏松月壤、崎岖地形、大坡度等复杂月面路况，通过性能显著优于大型移动平台，确保脱困工作顺利开展；配置多杆组接式锚定模块，锚杆采用长度2 m，直径150 mm 的空心圆柱构型，由于月壤的力学性质随着深度增加有明显的变化，60 cm 深处天然月壤承载能力超过55 kPa，当脱困机器人实现锚定后，锚杆能够产生的承载能力超过10 kN，能够为牵引脱困提供可靠支撑。

3.2 脱困流程设计

脱困流程如图5 所示，分为以下几个步骤实施：

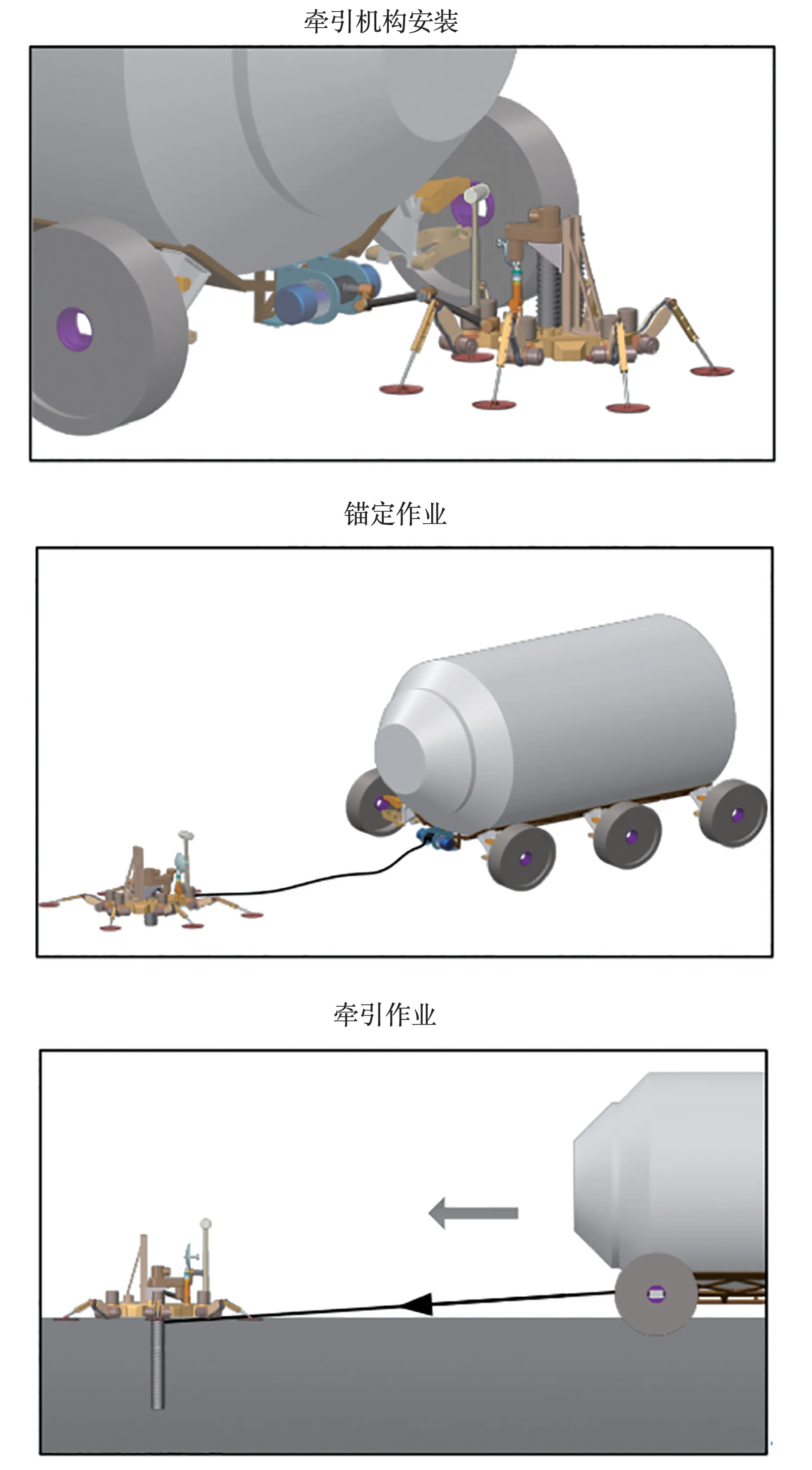
图5 脱困流程示意图Fig.5 Schematic diagram of the recovery process

1） 受困信息获取。大型移动平台通过车轮车身监视相机和雷达收集受困情况信息，包括各车轮沉陷深度、车身或底盘与月面障碍物接触情况和受困区域地形细节等，通过车载导航敏感器获得车身姿态和位置信息，结合驱动系统数据，分析得到各车轮滑移率，将相关数据信息下传至地面。

2） 脱困方案设计。地面根据接收的数据对车辆受困场景进行建模，识别受困工况，根据建模结果，通过理论计算或搭建地面实验场景重现受困工况，分析并确定牵引脱困需求，确定最优的牵引方向和牵引点，计算所需牵引力大小和牵引距离，确定锚定位置，完成脱困机器人路径规划，将相关信息上传至大型移动平台。

3） 脱困机器人部署。唤醒脱困机器人，建立大型移动平台与机器人之间的无线通信。解除脱困机器人与大型移动平台之间的机械锁定和电气连接，利用大型移动平台的转移操作设备将脱困机器人部署到月面。

4） 牵引机构安装。脱困机器人移动至规定的牵引点，将牵引机构的机架端安装到大型移动平台上，将绳索端安装到脱困机器人自身的连接机构处。

5） 脱困机器人移动至锚定位置。脱困机器人按照前期规划的路径移动至锚定点位。整个移动路径由多个间距1 m 的路径点组成，机器人以自主导航模式运行，地面指挥人员发送移动指令，经大型移动平台转发给脱困机器人，每次完成从一个路径点到下一个路径点的移动，移动过程中机器人自主完成导航与避障，直到移动至锚定位置。

6） 锚定作业。脱困机器人将锚定模块安装到工作位置并将其启动，利用内部进给机构压缩弹簧提供稳定钻压力，当进给量达到所设定的锚定深度后停止作业。

7） 牵引作业。启动牵引模块，以恒定速度卷收牵引绳，牵引绳绷紧后，大型移动平台缓慢驱动车轮低速旋转以辅助脱困，直至完成计划的牵引距离。

8） 解锚。再次启动锚定模块，以解锚模式运行，进给机构向上提升直至锚定模块回到初始位置。

9） 决策。判断大型移动平台是否实现脱困，若成功脱困则直接进入下一步，否则需地面决定是否再次尝试，若需要再次尝试，则重新设计脱困方案后，回到第5） 步；若不需再次尝试，则直接进入下一步。

10） 牵引绳回收。脱困机器人解除自身与牵引绳的连接，牵引机构卷收牵引绳直至完全收回。

11） 脱困机器人返回。地面指挥中心进行脱困机器人从锚定点到大型移动平台当前位置的路径规划并将相关数据上传，脱困机器人以第5）步相同办法沿路径返回，利用大型移动平台的转移操作设备回收脱困机器人，并建立机械锁定和电气连接，回收完毕后脱困机器人进入休眠状态。

4 脱困牵引力分析

脱困所需牵引力大小是牵引脱困任务的关键参数之一，这一参数与牵引角度直接相关。在执行脱困任务时，不同的锚定位置选择会使得牵引力的初始俯仰角度不同，另外在牵引过程中，随着大型移动平台向锚定点的不断靠近，牵引力俯仰角度也可能会发生变化。需要结合牵引俯仰角度对脱困所需牵引力进行分析，确定牵引力取值范围，为脱困系统的设计与设备选型提供参数支撑。

此外，由于月面是由大量微小月壤颗粒堆积形成的柔性砂地，难以用常规方法进行所需牵引力的计算分析。本节将月面简化为刚性地面进行计算，当移动平台在刚性地面受困时，所需脱困牵引力会大于柔性地面脱困。采用这种简化方法得到的结果能够包络实际数据，具有一定的合理性。

4.1 理论分析

4.1.1 沉陷工况

对于沉陷与障碍卡滞2 种受困工况，可以归纳为由于全部或部分车轮陷于可行驶路面以下导致行驶阻力显著增大，车轮所能提供的动力无法克服阻力，从而使得移动平台无法行驶而受困。根据这一分析可知，被陷车轮数量越多，行驶阻力增大越多，脱困难度则越大，当所有车轮全部沉陷时脱困难度最大。从包络分析的角度出发，整车沉陷工况所需的牵引力能够覆盖部分车轮沉陷或障碍卡滞工况，因此针对整车沉陷脱困进行分析。

脱困受力分析见图6。为便于分析，将地面对每个车轮的支持力和摩擦力分别等效为作用于质心的合力FN和φFN，FN与水平方向夹角为α，该角度与车轮半径R和沉陷深度h有关，φFN与FN垂直；牵引力FT作用于质心，与水平方向夹角为β，由于锚定点位在地面而牵引点在移动平台上，因此牵引力方向通常会偏向下方。利用力平衡法对大型移动平台进行受力分析，见式（9）。

求解该方程组得牵引力的表达式，见式（10）。

将该结果对β求一阶导函数，见式（11）。

令式（11）值为0，求解使FT取最小值的β值，得式（12）。

当式（10）分母为0 时，FT取值无穷大，即无论牵引力大小如何，移动平台都无法被牵引脱困，计算此时的极限β值为式（13）。

假设大型移动平台质量为8 t，车轮半径为550 mm，轮地附着系数取0.7，当牵引力方向水平向前，即β＝0 时，根据式（10）计算在该条件下不同沉陷深度所需牵引力大小，并绘制图线如图7所示。

图7 牵引力与沉陷深度曲线Fig.7 Curve of traction force with subsidence depth

由图7 可知，当大型移动平台沉陷深度约100 mm 时，脱困所需牵引力为0，该沉陷深度即为在此假设工况下沉陷受困的临界深度，根据式（2）可计算得该临界深度为99.42 mm。

针对牵引角度对所需牵引力的影响方面，以沉陷350 mm 为对象，根据式（10）计算在该条件下不同牵引角度所需牵引力大小并绘制曲线如图8 所示。

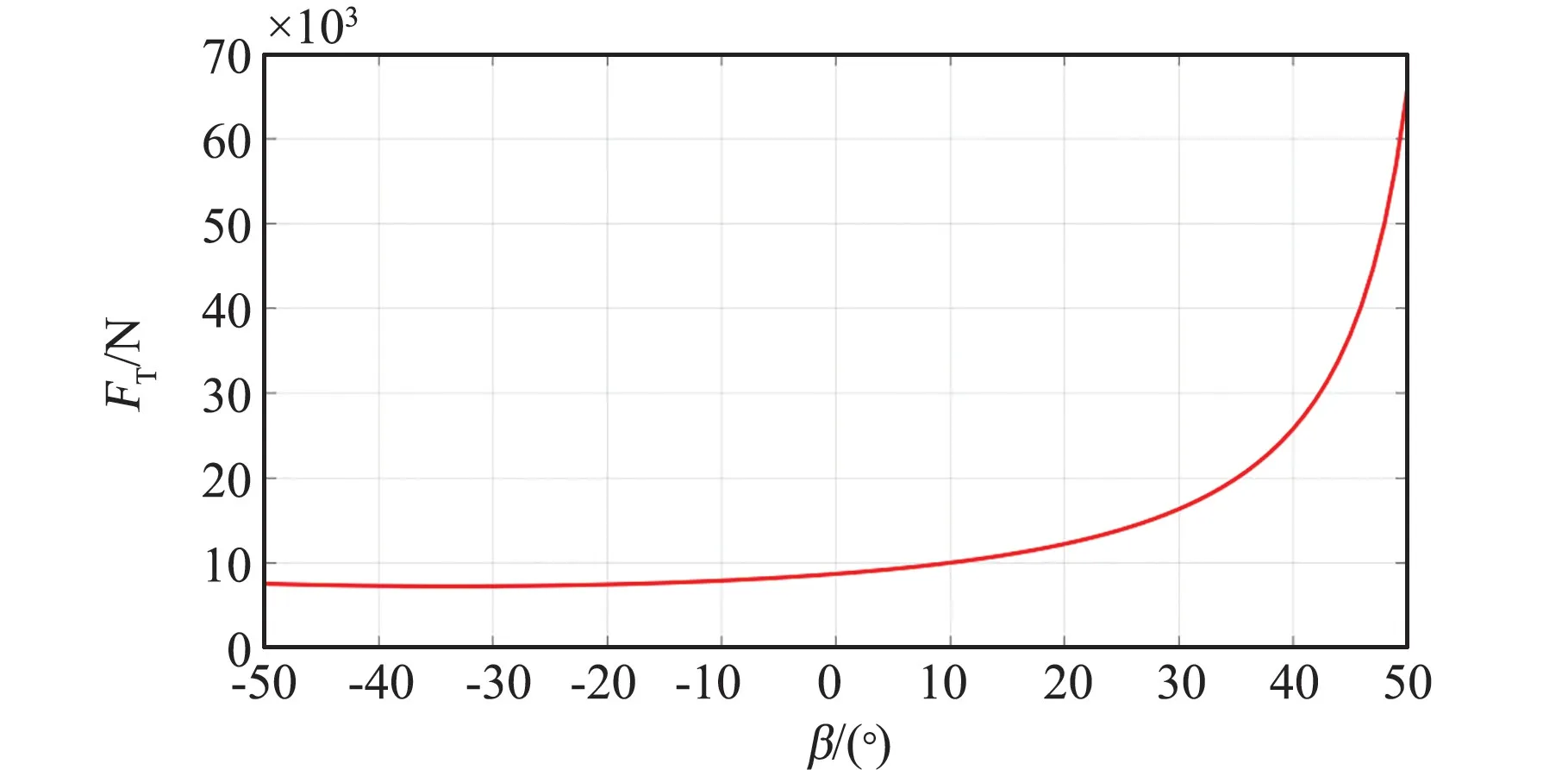
图8 牵引力与牵引角度曲线（沉陷350 mm）Fig.8 Curve of traction force with traction angle（Subsidence 350 mm）

由图可知，最佳牵引角度为负值，即牵引方向斜向上方，根据式（12）可计算得出在此假设工况下，最佳牵引角度为-33.68°；另外，当牵引角度接近临界角度时，所需牵引力将显著增大，根据式（13）可计算得出在此假设工况下，临界牵引角度为56.32°。

根据前文的分析，最佳牵引俯仰角数值均为负值，即牵引力最佳方向均斜向上方。在实际脱困作业时，应充分利用受困区域地形条件，合理选择锚定点和牵引点位置，使牵引力的俯仰角度尽可能接近推荐值，降低对脱困牵引力的需求。需注意牵引过程中应控制牵引力俯仰角度始终小于βlim，否则脱困所需牵引力值过大，无法有效实现脱困。

4.1.2 坡面工况

对于坡面受困，脱困受力分析见图9，同样将地面对每个车轮的支持力和摩擦力分别等效为作用于质心的合力FN和φFN，φFN与FN垂直；牵引力FT作用于质心，与坡面方向夹角为β。利用力平衡法对大型移动平台进行受力分析，见式（14）。

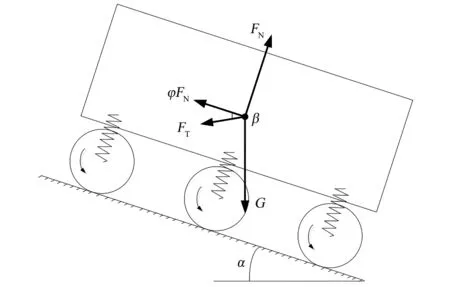
图9 坡面脱困受力分析图Fig.9 Diagram of slope recovery force analysis

求解该方程组得出牵引力表达式，见式（15）。

将该结果对β求一阶导函数，见式（16）。

令式（16）值为0，求解使FT取最小值的β值，得式（17）。

当式（15）分母为0 时，FT取值无穷大，即无论牵引力大小如何，移动平台都无法被牵引脱困，计算此时的极限β值为式（18）。

根据式（8），当坡面角度大于arctanφ时，大型移动平台会发生受困，牵引脱困过程中若牵引角度达到βlim，牵引方向将垂直向上，此牵引角度在实际操作过程中发生概率较低，但仍应尽可能避免过大的牵引仰角，降低对牵引力的需求。

假设大型移动平台质量为8 t，车轮半径为550 mm，轮地附着系数取0.7，当牵引力方向与坡面平行，即β＝0 时，根据式（15）计算在该条件下不同坡度所需牵引力大小，并绘制曲线如图10所示。

图10 牵引力与坡面角度曲线Fig.10 Curve of traction force with slope angle

由图10 可知，当坡面角度达到35°左右时，脱困所需牵引力为0，该角度即为在此假设工况下坡面受困的临界角。根据式（8），假设车辆几何设计合理，未出现质心投影超出车轮包络范围的现象，则可计算得该临界角度为34.992°。

针对牵引角度对所需牵引力的影响方面，以坡面角度40°为对象，根据式（15）计算在该条件下不同牵引角度所需牵引力大小并绘制曲线如图11 所示。

图11 牵引力与牵引角度曲线（40°坡面）Fig.11 Curve of traction force with traction angle（40° slope）

由图11 可知，最佳牵引角度为正值，即牵引方向相对于坡面斜向下方。根据式（16），可计算得到该工况下最佳牵引角为34.992°，与临界受困坡度在数值上一致。当牵引角度接近临界角度时，所需牵引力也将显著增大。综合以上分析，沉陷受困的脱困难度较坡面受困更大，在一般的受困工况下，脱困所需牵引力将主要集中在10 kN以下，数值范围合理，可为后续脱困设备设计提供数据支持。

4.2 仿真验证

利用Adams 动力学仿真软件搭建月面大型移动平台脱困系统动力学模型。

对于沉陷工况，将移动平台放置在不同深度的坑道中并驱动车轮定速旋转以实现受困模拟。在车身底盘处施加单向作用力作为脱困牵引力，设置作用力大小从0 开始逐渐增大，当移动平台质心高度第一次由负值升高到0 时，视为成功脱困，抓取此时的作用力大小作为该工况下的脱困所需牵引力并进行记录，即得到不同受困工况下牵引脱困的仿真结果。部分仿真图像如图12所示。

图12 沉陷脱困动力学仿真Fig.12 Dynamic simulation of subsidence recovery

统计不同沉陷深度所需脱困牵引力的仿真值，并将其与理论计算得到的数据进行对比，如图13 所示。

图13 牵引力与沉陷深度对比曲线Fig.13 Comparison curve of traction force with subsidence depth

从图中可以看出，沉陷深度小于400 mm 时，仿真结果和理论计算结果一致性较高；当沉陷深度超过400 mm 后，仿真模型中移动平台的底盘与地面接触，使得移动平台实际沉陷量没有达到要求值，所需牵引力偏低。从该结果可以看出，理论计算值在较小沉陷量时的可靠性较高，随着沉陷量进一步增大，底盘与地面接触后，车身部分重量被地面支承，脱困所需牵引力随沉陷量增大的增长速度放缓。

将沉陷量固定为350 mm，改变牵引力作用方向，采用同样方法抓取质心高度上升到0 时的作用力大小，得到不同牵引角度下的所需牵引力数值，并于理论结果进行对比，如图14 所示。

图14 牵引力与牵引角度对比曲线（沉陷350 mm）Fig.14 Comparison curve of traction force with traction angle（Subsidence 350 mm）

从图中可以看出，仿真结果和理论计算结果整体上一致性较高，接近极限角度时，仿真值偏低，此时牵引力数值过大，仿真模型出现部分失效导致结果失真。在实际任务过程中出现类似极限工况的概率较低，可忽略此偏差。

对于坡面受困工况，将移动平台放置在不同角度的坡面上，并驱动车轮定速旋转以实现受困模拟。在车身底盘处施加单向作用力作为脱困牵引力，设置作用力大小从0 开始逐渐增大，当移动平台质心高度发生明显升高时，视为成功脱困。抓取此时的作用力大小作为该工况下的脱困所需牵引力并进行记录，即得到不同受困工况下牵引脱困的仿真结果。部分仿真图像如图15 所示。

图15 坡面脱困动力学仿真Fig.15 Dynamic simulation of slope recovery

统计不同坡度所需脱困牵引力的仿真值，并将其与理论计算得到的数据进行对比，如图16 所示。从图中可以看出，仿真值与理论值表现出一致的变化趋势，吻合良好，牵引力随坡度的增大而增大，在35°～60°区间内近似呈线性增长关系。

图16 牵引力与坡度角对比曲线Fig.16 Comparison curve of traction force with slope angle

将坡度固定为40°，改变牵引力作用方向，采用同样方法抓取质心高度出现明显上升时的作用力大小，得到不同牵引角度下的所需牵引力数值，并于理论结果进行对比，如图17 所示。

图17 牵引力与牵引角度对比曲线（40°坡面）Fig.17 Comparison curve of traction force with traction angle（40° slope）

从图中可以看出，理论计算结果与仿真结果吻合良好，牵引角度在-40°～50°范围内，随着角度的增大，牵引力先减小再趋于稳定，最后略微增大，在35°左右取到最小值。

从以上结果可以看出，理论计算值与仿真结果一致性较好，平均相对误差均在10%以下，脱困所需牵引力的计算方法以及对最佳牵引角和极限牵引角的判断方法均具有较高的可靠性，牵引脱困的受力模型简化较为合理，可为后续设计工作提供参考。

5 结论

本文针对月面大型移动平台月面受困问题，结合月面特殊环境分析可能受困工况，提出了一种采用脱困机器人锚定并牵引的脱困方案设想。结合牵引角度对脱困所需牵引力进行分析，得出了不同受困工况下所需牵引力的计算方法，并通过动力学仿真加以验证。结果表明，脱困所需牵引力计算方法可靠，常见受困状态下所需牵引力在10 kN 以下，脱困方案具备较强可行性。

后续将采用离散元分析方法对月壤力学环境进行建模，分析在牵引过程中大型移动平台在月面的力学行为以及锚定设备在月壤中的承载能力，并通过试验验证，进一步提高脱困模型的准确性和脱困方案的合理性。