基于随机参数Logit模型的车辆冲突风险影响因素研究

温惠英,成 杰,赵 胜

(华南理工大学 土木与交通学院,广东 广州 510640)

0 引 言

随着我国机动车拥有量和公路里程增加,交通安全问题日益严峻,严重威胁着道路使用者的生命财产安全。为减少交通事故发生并降低事故危害,有必要主动对事故风险进行识别,而对交通事故风险的影响因素进行研究是风险识别的基础。

目前已有大量针对事故风险影响因素的研究,根据数据来源大致可分为传统的基于事故数据的影响因素分析和基于安全替代措施的影响因素分析两类。基于事故的影响因素分析主要以事故数据为基础,选取驾驶员特性、车辆类型、道路线形、环境等多种因素作为自变量[1],以是否发生事故或事故的严重程度[2]为因变量,建立模型进行分析。在使用的模型方面,Logit模型[3-4]、负二项回归模型[5]、机器学习[6]等均被用于研究,但最为常用的是以Logit模型为代表的传统离散选择模型。

但由于交通事故数据存在统计周期长、数量少,导致基于事故数据的研究存在局限性。该类研究多基于事故发生前后较长时间的宏观数据,研究范围集中在宏观尺度,较少考虑事故发生前后交通状态对事故发生的影响。

为了弥补这些缺陷,研究者提出了基于交通冲突的冲突替代技术。研究显示,交通事故和交通冲突存在强相关性[7]。与事故数据相比,交通冲突指标获取容易、样本量大,可更好反映事故风险发生前后车辆和交通流状况及变化过程[8]。

随着道路检测设备的发展及计算机图像处理技术的进步,视频数据[9]、路侧感知数据[10]、自然驾驶数据[11]等可以描述每辆车运动特征的微观多源数据得以用于实时微观风险研究。与以往基于事故数据的研究不同,微观风险研究多使用冲突替代指标建立模型,研究前后车速度差、车头间距等车辆间微观交互特征[12-13]对风险的影响,并发现碰撞风险会受到微观行为影响。在研究方法上,Logit模型也[14]被广泛使用。

目前的研究很少将微观和宏观特征同时纳入模型进行分析,没有全面考虑各类因素影响,且使用的时间片数据较长,不能很好描述风险发生前的交通特征。综上,笔者基于车辆微观轨迹数据集(HighD数据集),使用交通冲突指标表征风险,提取冲突风险前1 s内的数据进行处理,同时综合考虑车辆自身运动状态、与周围车辆的交互以及宏观交通流状态三方面因素,并考虑到数据异质性,分别建立随机参数和均值异质性随机参数Logit模型,对车辆冲突风险的影响因素进行研究。

1 数据准备

1.1 HighD数据集介绍

HighD数据集(the highway drone dataset)是一个使用无人机拍摄的2017、2018年德国高速公路的自然车辆轨迹的数据集,覆盖范围约420 m。研究团队使用了先进算法对数据进行后处理[15],定位误差小于10 cm,每秒包含连续的25帧信息。每条轨迹数据都包含车辆的运动特征和物理特征,包括车辆的ID、车辆类型、横向和纵向位置、速度、加速度、车道、TTC等。由于该数据集有数据详细、高分辨率、低误差的优点,被广泛运用于各类研究。

1.2 冲突风险样本数据提取

交通冲突是交通参与者相互作用产生的,含义为在时间或空间上接近到一定程度,如果不采取规避措施改变运动状态将发生碰撞事故,是事故的前兆,目前最常用的冲突指标是碰撞时间tTTC。tTTC的定义为:当后车速度大于前车时,若两车继续以当前速度行驶且不改变行驶轨迹,后车与前车距离碰撞发生的剩余时间计算如式(1):

(1)

式中:VF为后车速度;VP为前车速度;xF为后车位置坐标;xP为前车位置坐标;lF为后车长度。

tTTC反映了两车的接近程度,tTTC值越小,说明两车发生事故的风险越大。为此,研究使用tTTC作为事故风险识别的指标。根据文献[16],选择2 s作为风险判定的阈值,即当tTTC小于2 s时,认为存在碰撞风险。

由于越接近碰撞发生时刻的交通参数重要性越强,将tTTC小于2 s的时刻记为零时刻,选取零时刻前1 s的原始轨迹数据,提取车辆在横、纵向上的微观运动特征,并对其进行处理得到冲突风险前1 s的微观及宏观交通流特征。

此外,为了比较正常情况下的交通状况与存在风险时的差异,还需要提取正常情况的样本。参考文献[17],采用病例对照的方法,选取的风险样本与正常样本比例为1∶4。为排除风险事件对正常交通流存在的后续影响,在提取正常样本时不考虑风险发生前后20 s内的数据。在正常样本提取时,为更好反映分布情况,将tTTC始终大于2 s且满足要求的数据按四分位数分为4组,从每组中等比例随机抽样,最终得到240个风险样本和960个正常样本。

2 指标选取及模型建立

2.1 指标选取

目前的安全评价相关研究中,根据使用数据的不同,模型选用的自变量主要可分为宏观交通流特征(如流量、密度、平均速度、大车比例等)和微观特征(速度、加速度、车头间距等)两大类。研究表明,不仅微观因素对交通冲突风险有较强影[18],宏观交通流状态与冲突间也存在显著关联[19]。为更全面研究影响冲突风险的因素,笔者从车辆自身运动状态、与周围车辆微观交互、车道宏观交通流状态3个方面选取指标以建立模型。

由于HighD数据集每秒有25帧,需将原始数据处理得到每秒的时间片段数据,所选变量及特征描述如表1。其中车辆自身运动状态、与周围车辆的交互两类特征为微观特征,分车道宏观参数为宏观特征。

表1 选取的特征变量

在初步选取了模型变量后,对特征变量进行筛选,去除与因变量相关性不高的变量,以提高模型效率。笔者使用皮尔逊相关系数(以下简称相关系数)和嵌入法进行特征变量选择。

相关系数是反应变量间相似程度的统计量,常用于特征变量选择,相关系数小于0.2则认为两特征变量之间相关性弱[20]。仅使用相关系数无法很好地对变量进行选择。为此,结合机器学习常用的特征选择算法嵌入法(embedded)对特征进行选择。

嵌入法是一种特征选择和算法训练同时进行的方法,其特点是结合要使用的模型并根据模型评估结果进行特征选择,且每次都会遍历所有特征。相比于其他特征选择算法,嵌入法的结果直接基于模型的效用得出,考虑了特征对模型的贡献,能更好提升模型效果。而逻辑回归由于带有L1和L2惩罚项,可以得到相关特征的权值系数,其中L1正则化会在逐渐加强的过程中把对模型贡献不大的特征的参数变成0,留下对模型有较大贡献的特征,其本质是一个特征选择的过程。由于L1正则化的特质,逻辑回归的特征选择可以由嵌入法来完成,其系数能衡量特征的重要程度和贡献度,从而筛选出让模型高效的特征。

由于Logit模型和逻辑回归模型(logistic regression)原理相同并可以相互转化,采用基于逻辑回归L1正则化的嵌入法对特征进行进一步筛选,并结合相关系数选择以下特征变量,如表2。

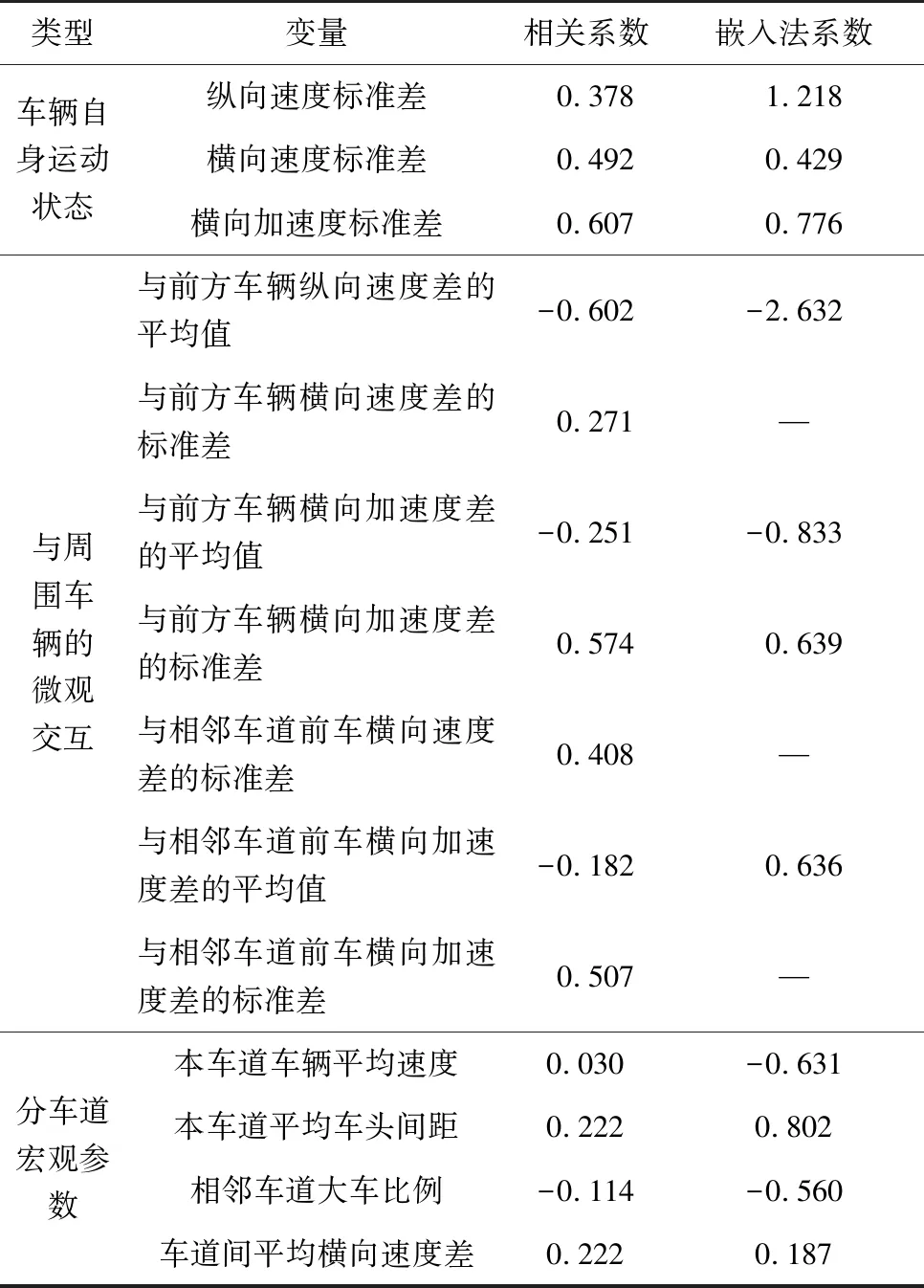
表2 筛选后特征

2.2 二元Logit模型

2.2.1 普通二元Logit模型

为研究冲突风险与影响因素的关系,建立二元Logit模型。Logit是离散选择模型的一种,常用于分类问题。由于Logit模型可表示一个因变量和多个互不相关的自变量间的回归关系,常用于因变量是二值变量的影响因素分析。设存在冲突风险的样本为y=1,正常样本为y=0,风险发生概率分别为p和1-p。

…+βkxk=β0+βkX

(2)

式中:β0为函数的常数项;X为自变量向量,即冲突影响因素;k为影响因素的个数;βk为自变量对应的系数向量。

在传统Logit模型中,每个解释变量的系数固定,即各影响因素在不同样本中的影响程度相同。但实际中,同一变量对于不同样本的影响并不固定。由于风险的复杂性,在建模过程中存在无法被观测的因素,且已有变量在不同样本上也存在差异,这些都会产生异质性。

2.2.2 随机参数Logit模型

随机参数模型通过将模型中的变量参数设置为固定参数和随机项的组合,使变量系数可变化,降低异质性影响。随机参数Logit模型如式(3)、式(4):

(3)

βi=β+Γδi

(4)

式中:βi为样本i的自变量Xi对应的参数向量,服从某种分布,即βi～f(βi|θ);β为Xi对应的随机参数向量的均值向量,对所有样本都相同;Γ为系数矩阵,表征各随机参数间协方差及潜在相关性,其元素用于计算随机参数的标准差,其对角线元素表示随机参数的标准差;δi为协方差矩阵,是单位阵的随机项,服从标准正态分布,用于表征异质性。

2.2.3 考虑均值异质性的随机参数Logit模型

随机参数Logit模型不能解释造成随机系数的原因,为此引入考虑均值异质性的随机参数Logit模型,即设定随机参数的均值中存在未观察到的异质性。在式(4)基础上加入均值异质性向量,即:

βi=β+ΔZi+Γδi

(5)

式中:Zi为样本i中的均值异质性向量,会影响βi的均值;Δ是对应的估计参数向量。

由于随机参数Logit模型的概率函数为非封闭型,不能直接求解,需要采用基于仿真的最大似然方法。参考文献[21],选择Halton序列抽样,抽样次数为500次,且随机参数服从正态分布的效果更好。

由于Logit模型是非线性模型,其系数只能反映自变量x和响应概率p的关系为正向还是负向,而无法进一步解释自变量x对p的影响。因此,引入边际效应来说明变量的变化对冲突风险的影响情况[2]。边际效应可以解释为当其他变量保持不变时,某个自变量变化一个单位引起的响应概率变化,连续变量的边际效应本质是求偏导数,自变量xk的边际效应M计算如式(6):

(6)

2.3 模型拟合评价

为比较模型的拟合优度和预测精度,本文使用赤池信息准则(AIC)和McFaddenR2(McFadden’s likelihood ratio index)进行模型拟合评价。

2.3.1 AIC赤池信息准则

AIC值越小,证明模型拟合效果越好。AIC统计量如式(5):

AAIC=-2(LL-K)

(7)

式中:LL为待评估模型的对数似然函数值;K为模型中参数数量。

2.3.2 McFaddenR2(伪R2)

McFaddenR2的取值范围为0到1。待评估模型的McFaddenR2越大,则其相对于基准模型的提高程度越大,计算如式(8):

(8)

式中:LL0是基准模型的最大对数似然值。

3 模型结果与分析

3.1 模型比较

使用第2节选取的变量进行建模,去除其中不显著的变量,保留所有显著变量作为最终的建模变量。对普通二元Logit模型、随机参数Logit模型以及均值异质性随机参数Logit模型进行参数标定后,得到参数的结果和模型拟合指标如表3。

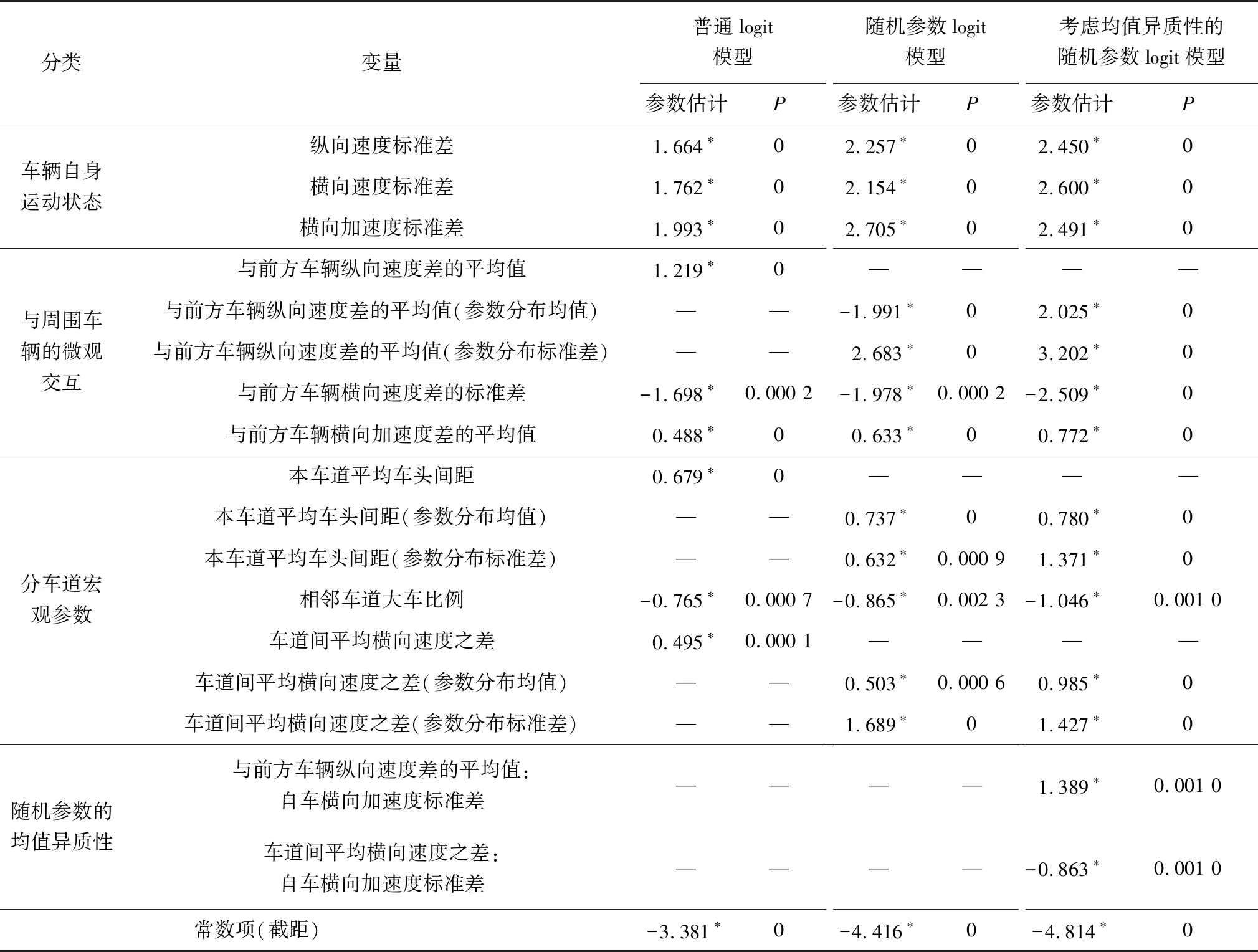
表3 模型参数估计结果

由表3可知:

1)3个模型中,纵向速度标准差、横向速度标准差、横向加速度标准差、与前方车辆纵向速度差的平均值、与前方车辆横向速度差的标准差、与前方车辆横向加速度差的平均值、本车道平均车头间距、相邻车道大车比例、车道间平均横向速度之差等9个变量在99%的置信水平上显著。

2)与前方车辆纵向速度差的平均值、本车道平均车头间距、车道间平均横向速度之差等3个变量的系数为随机参数,其系数均值和标准差均在99%的置信水平上显著,说明存在异质性。

模型拟合优度指标如表4。由表4可知:相比普通二元Logit模型,随机参数Logit模型的对数似然值由-172.996提高至-157.619,均值异质性随机参数Logit模型的对数似然值提高至-147.453;均值异质性随机参数Logit模型的AAIC值最小,且其RMcFaddenR2最大。可知均值异质性随机参数Logit模型拟合效果最好,随机参数Logit模型次之,普通二元Logit模型最差。

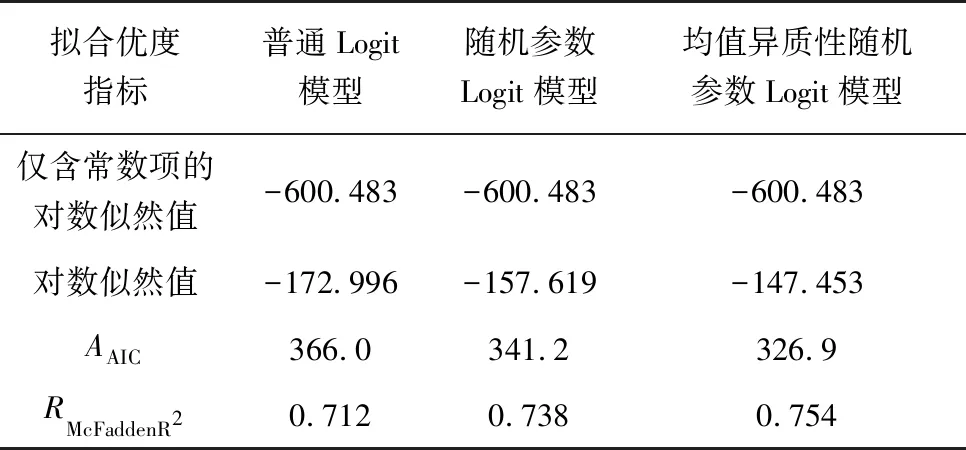
表4 模型拟合优度指标对比

3.2 参数解释

由于考虑均值异质性的随机参数Logit模型的拟合效果更好,将结合表3考虑均值异质性的随机参数Logit模型结果和表5边际效应结果对参数进行分析,并对影响因素进行分析。

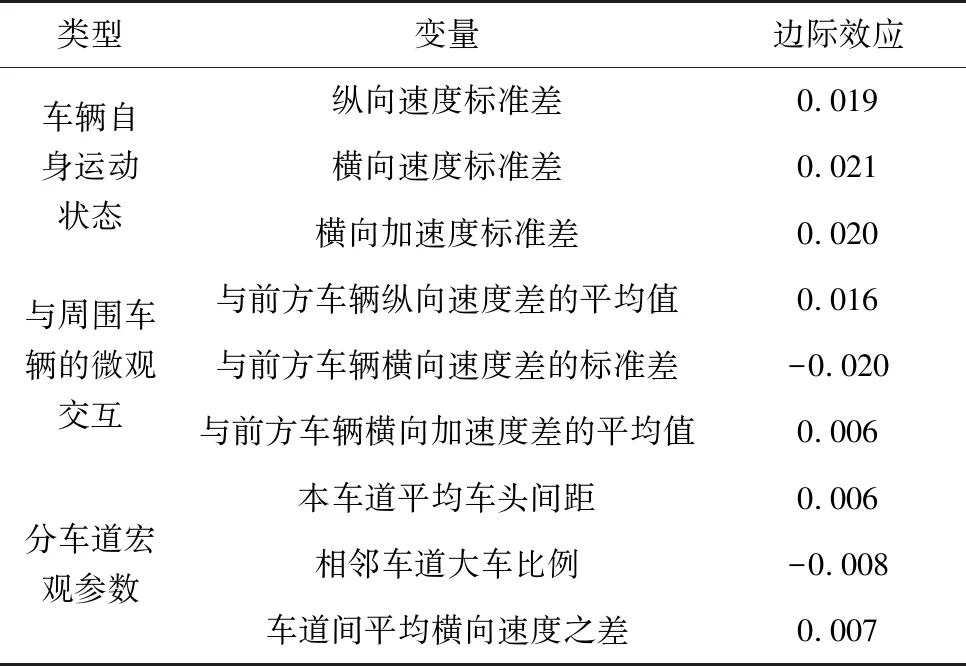
表 5 均值异质性随机参数Logit模型的边际效应

3.2.1 车辆自身运动状态

结合表3、表5可知:

1)在车辆自身运动状态变量中,车辆纵向速度标准差、横向速度标准差、横向加速度标准差均对冲突风险有显著影响,并且均与冲突风险呈正相关。

2)纵向速度标准差每增加一个单位,风险发生可能性增加1.9%。纵向速度标准差增大说明当前车辆的纵向速度出现较大的波动,可能存在急加速或急减速等危险驾驶行为,导致风险增加。

3)横向速度标准差每增加一个单位,风险发生可能性增加2.1%。车辆的横向速度出现较大波动时,说明其可能存在换道、分神驾驶或者疲劳驾驶等行为,或通过转向来避免追尾冲突,与周围车辆交互增多,导致冲突风险增大。

4)横向加速度标准差每增加一个单位,风险发生可能性增加2.0%。横向加速度的波动性增大会导致驾驶员对于车辆的控制更难,产生风险可能性更大。

3.2.2 与周围车辆的交互

由表3、表5可知:

1)在表征与周围车辆交互的变量中,与前方车辆纵向速度差的平均值、与前方车辆横向速度差的标准差、与前方车辆横向加速度差的平均值均对风险有显著影响。

2)与前方车辆纵向速度差的平均值是随机变量,其参数服从均值为2.025、标准差为3.202的正态分布,该参数大于0的概率为73.64%,即随着与前方纵向速度差的增大,有73.64%的个体碰撞风险可能增高;车辆与前车的平均纵向速度差边际效应为0.016,说明与风险呈正相关,即其每增加一个单位,风险发生可能性增加1.6%。这是由于当两车纵向速度差较大时,跟随车辆速度大于前车,发生追尾冲突的风险也随之增大。

3)由均值异质性随机参数Logit模型结果可知,变量“与前方车辆纵向速度差的平均值”的随机参数均值会受到“自车横向加速度标准差”的影响,其参数估计为正,这说明当车辆的横向加速度标准差增大时,变量“与前方车辆纵向速度差的平均值”的参数均值增大,即发生冲突风险的概率增加。这可能是由于车辆的横向加速度波动影响驾驶员对车辆的控制水平,间接导致与前车车速差增加,或者车辆在换道过程中进行加速超车,从而造成风险增大。

4)当前车辆与前方车辆横向速度差的标准差、与前方车辆平均横向加速度差均为固定参数变量,边际效应分别为-0.020和0.006,即与前方车辆横向速度差的标准差每增加一个单位,风险发生的概率降低2%,这可能是由于此时车辆正处于换道过程中,逐渐远离目标车辆,追尾风险下降;而与前方车辆横向加速度差的平均值每增加一个单位,风险发生的概率上升0.6%,这说明此时前车横向速度变化更为剧烈,导致目标车辆追尾风险略有增加。

3.2.3 分车道宏观参数

由表3、表5可知:

1)在宏观交通流特征中,本车道的平均车头间距、相邻车道的大车比例、车道间的平均横向速度差对风险有显著影响。其中本车道的平均车头间距和车道间平均横向速度差为随机参数变量。

2)本车道平均车头间距的系数服从均值为0.780,标准差为1.371的正态分布,表明该系数大于0的概率为71.5%,即随着车道平均车头间距的增大,有71.5%的个体冲突风险可能增加。可能是当该车道的平均车头间距较大时,可能诱发相邻车道车辆的换道行为,而换道过程中车辆交互频繁,从而导致风险增加,这与文献[10]的结论相似。车道平均车头间距的边际效应为0.006,即车道的平均车头间距每增加一个单位,风险发生的可能性就会增加0.6%。而本车道平均车头间距作为随机参数变量没有检测出显著的均值异质性的变量,表明这一变量具有异质性,但基于笔者数据还不能对其异质性问题进行解释。

3)车道间平均横向速度差的系数服从均值为0.985,标准差为1.427的正态分布,表明该系数大于0的概率为75.5%,即随着目标车辆所在车道与相邻车道平均横向速度差的增大,有75.5%的个体碰撞风险可能增大;其边际效应为0.007,即每增加一个单位,风险发生的概率就增加0.7%,可以解释为当前车道中有车辆处于换道过程,导致车道平均横向速度增大,而换道过程中出现的车辆交互影响当前车道其他车辆,也可能使目标车辆风险增大。

4)根据均值异质性随机参数logit模型的结果,随机参数变量“车道间平均横向速度差”的参数均值会受到变量“自车横向加速度标准差”的影响,其参数估计为负。说明当车辆的横向加速度标准差减小时,变量“车道间平均横向速度差”的参数均值增大,即由车道间平均横向速度差引起风险的概率增大。说明在冲突风险前1 s内车辆的横向加速度波动程度的降低反映在车道宏观特征变量上有所滞后,即使此时车辆的横向加速度变化很小,也可能会造成风险增加。

5)相邻车道大车比例的参数为固定值,与风险呈负相关,其边际系数为-0.008,说明相邻车道的大车比例每增加一个单位,风险发生的概率降低0.8%。这是由于当相邻车道的大车较多时,本车道车辆倾向于保持车道行驶,并注意与前车的安全距离,从而使冲突风险略有下降。

4 结 论

选取HighD高分辨率轨迹数据集,使用TTC作为风险判别指标并建立Logit模型对冲突风险的影响因素进行分析。提取风险发生前1 s内的车辆轨迹数据,从车辆自身运动状态、与周围车辆的微观交互以及宏观交通流状态3个方面计算特征变量,并使用特征选择算法进一步筛选出用于模型的特征。最后以是否存在碰撞风险为二元因变量,分别建立了普通二元Logit模型、随机参数Logit模型和考虑均值异质性的随机参数Logit模型,得到如下结论:

1)对数似然、AAIC、RMcFaddenR2等模型拟合评价指标的结果表明,均值异质性随机参数Logit模型相比普通二元Logit模型有更好的拟合效果最好,随机参数Logit模型次之。

2)车辆自身的运动状态、与前方车辆的交互以及宏观交通状态均对冲突风险有显著影响。其中影响最大的特征依次是:车辆横向速度标准差、与前方车辆横向速度差的标准差、车辆横向加速度标准差以及纵向速度标准差、相邻车道大车比例。相比于车辆自身运动特征以及与前方车辆交互特征,在冲突风险前1 s内,宏观交通特征的影响更小。

3)当车辆自身的速度和加速度波动增大时,其冲突风险可能性增大;当车辆与前方车辆的速度差增大时其风险可能性增大;本车道的平均车头间距越小,车辆的风险性更大,相邻车道的大车比例增大,车辆风险有所下降、而车道间平均横向速度之差对风险有正向影响。