城市公交网络的有限时间平衡性问题

张春梅,李 冉,阳 惠

(西南交通大学 数学学院,四川 成都 610031)

0 引 言

复杂网络大量存在生活中,如电力网络、交通网络、 社交网络等[1-3]。并且其在自然科学中也具有广泛的应用[4-6]。而同步是复杂网络中的普遍现象,在近几十年中,大量学者在其相关领域的同步性研究中做出了重要贡献,尤其在交通领域。文献[7]研究了复杂网络的同步问题及其在交通领域的应用。文献[8-11]研究了多权值复杂公交网络的同步问题,并对复杂公交网络动态特征做了一定研究。文献[12]针对公交网络的拓扑结构进行分析,得到公交网络是具备小世界网络特征的复杂网络的结论。

上述研究的城市公交网络同步的时间是不确定的,因此其控制成本较大且无法估计同步的时间。而有限时间的城市公交网络同步,可以很好地估计出同步的时间,更有实用价值。目前关于城市公交网络的有限时间平衡问题的研究结果还很少。而有限时间平衡作为城市公交网络的一个重要特征,其对于城市公交网络的平衡运行以及整个城市交通系统的正常运行都具有重要意义。因此很有必要研究城市公交网络有限时间平衡问题。

在城市公交网络中,交通事故、环境、噪声等随机因素干扰不可避免地存在,而且这些随机干扰会影响城市公交网络的平衡运行。同时,公交车在行驶过程中要求司机对各种状况做出正确的反应,这必然存在时间的延迟。因此将随机扰动和时间延迟考虑在城市公交网络中可以使得模型更贴近实际。

借助复杂网络有限时间控制策略、稳定性理论和图论方法[13-16],研究城市公交网络的有限时间平衡问题。主要结论如下:第一以公交线路为网络节点,采用R空间建模方法,借助驱动-响应系统概念,建立城市公交网络模型;第二基于图论中的基尔霍夫矩阵树定理,间接构建全局李雅普诺夫函数,使得驱动-响应系统在有限时间内达到同步;第三通过合理的交通调度(调节控制器的可变参数)使得受到随机扰动的城市公交网络(公共汽车交通网络)与理想状态下平衡运行的城市公交网络在有限时间内达到同步(运行状态达到一致),并给出了同步的具体时间。即受到随机干扰的城市公交网络能在有限时间内恢复平衡运行。

1 模型构建和预备知识

1.1 符号介绍及相关定义

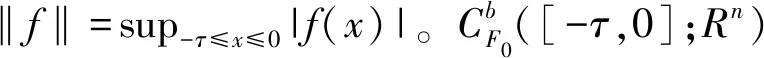
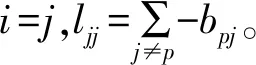
dx(t)=f(t,x(t),x(t-τ))dt+g(t,x(t)

x(t-τ))d(t)

(1)

式中:时滞τ是正数;(t)表示一维标准布朗运动;函数f,g:R+×Rn×Rn→Rn均满足局部利普希茨条件和线性增长条件[16]。

1.2 模型描述

笔者采用R空间建模方法,以公交线路(例如1路、 2路)为网络节点,若两条公交线路上有相同的停靠站,则节点之间连接有向的边,建立城市公交网络模型。在实际生活中,司机反应时间会导致信息传输的延迟,因此需要将时滞考虑到顶点中。每个顶点(每条公交线路)的动力学行为可以表示为:

(2)

式中:xh=(xh1,xh2,…,xhn)T∈Rn为第h条公交线路的状态向量;τ为公交线路上司机反应,交通拥堵等导致的信息传输延迟的时间,fh(t,xh(t),xh(t-τ)):R+×Rn×Rn→Rn为非线性连续函数(表示第h条公交线路的动力学行为),对于每一个顶点h,f是连续可微的。M={1,2,…,M}。

另外,以公交线路为网络节点,不同公交线路所连的边上可以考虑线路长度、拥挤度、换乘系数等多种影响公交线路运行的因素。从而,可以将城市公交网络看作是 一个多权值的复杂网络,笔者将其抽象成一个加权有向图 (G,B)。其中,有向图G带有M个顶点和q种权重(M个顶点表示M条公交线路,q种权重表示影响公交线路运行的q种因素)。借助驱动-响应系统的概念,驱动系统表示理想状态下每条公交线路构成的平衡运行的耦合系统,表达为:

(3)

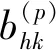
在现实情况下,一些随机因素(交通拥堵、交通事故等)对驱动系统(理想状态下公交线路构成的耦合系统)造成一定的影响(例如车辆大量聚集),使其不能够平衡运行。因此,希望通过合适的交通调度,使得受到随机扰动后实际运行的城市公交网络和理想状态下的城市公交网络运行状态达到一致。对于驱动系统(3),将考虑了随机扰动和交通调控的系统作为响应系统,则其表达式为:

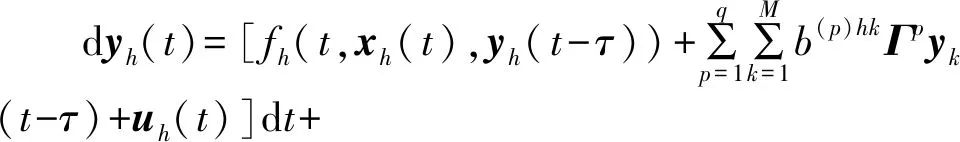
gh(t,xh(t),xh(t-τ))]d(t)

(4)

式中:yh(t)=(yh1,yh2,…,yhn)T∈Rn为第h条公交线路的实际状态向量;gh(t,yh(t),yh(t-τ))-gh(t,xh(t),xh(t-τ))为第h条公交线路的随机影响因素的强度函数;uh(t)为第h条公交线路上时变的交通调度。

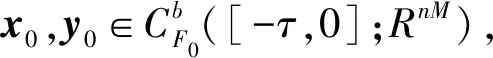
令:eh(t)=yh(t)-xh(t)

eh(t-τ)=yh(t-τ)-xh(t-τ),h∈M

基于驱动-响应系统(3)和系统(4)可以得到误差系统为:

deh(t)=[fh(t,yh(t),yh(t-τ))-

uh(t)]dt+[gh(t,yh(t),yh(t-τ))-

gh(t,xh(t),xh(t-τ))]d(t),h∈M

(5)

因此,驱动系统和响应系统的同步等价于误差系统零解的稳定性。笔者的主要工作就是通过合适的交通调度,使得考虑时滞、多权值、随机干扰等实际运行的城市公交网络能够在有限时间内恢复平衡运行这样不仅可以快速缓解交通系统的压力,而且可以节约人力、物力的消耗。

对于误差系统的第h个方程,用一个微分算子L作用在Vh∈C1,2(R+×Rn;R+)有:

(6)

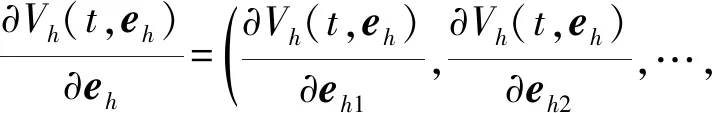
定义1：如果:

则称驱动系统(3)与响应系统(4)实现同步。

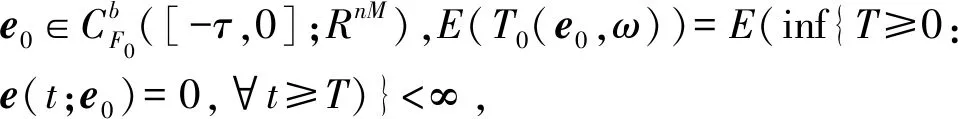
2 主要结果

首先构造单个顶点的李雅普诺夫函数,然后结合基尔霍夫矩阵树定理,间接得到整个城市公交网络的全局李雅普诺夫函数。基于图论知识、有限时间控制策略、稳定性理论以及随机分析的理论,使得驱动-响应系统在有限时间内达到同步。为了完成定理的证明,首先介绍如下假设和定义。

假设A1:对于h∈M,存在非负常数sh和lh使得:

|gh(t,yh,xh)-gh(t,vh,uh)|≤

sh|xh-uh|+lh|yh-vh|,t∈R+,xh,yh,uh,vh∈Rn

假设A2:对于h∈M,存在非负常数ch和dh使得:|fh(t,yh,xh)-fh(t,vh,uh)|≤ch|xh-uh|+dh|yh-vh|,t∈R+,xh,yh,uh,vh∈Rn

引理1：对于误差系统,如果存在一个正定二次 连续可微的径向无界李雅普诺夫函数V:R+×RnM→R+,使得:LV≤-ηVρ(e)。其中常数η>0,0<ρ<1,则系统的平凡解全局有限时间吸引,且E(T0(e0,ω))≤V1-ρ(e0)/(η(1-ρ)),同时T0(e0,ω)<∞,a.s. 为了方便,用:

表示加权矩阵。

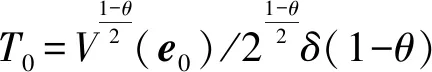
(7)

式中:0<θ<1;R和G是足够大的正数。

证明第1步:构建单个顶点的李雅普诺夫函数:

(8)

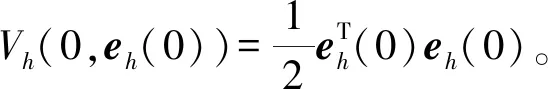
gh(t,xh(t),xh(t-τ))]T×[gh(t,yh(t),yh(t-τ))-

(9)

结合图论知识间接构建全局的李雅普诺夫函数为:

(10)

式中:γh为(G,(Dhk)M×M)的拉普拉斯矩阵的第h个对角元素的余子式。

通过计算可以得到:

(11)

通过使用文献[13]的基尔霍夫矩阵树定理,可以得到:

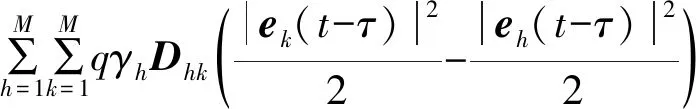
(12)

(13)

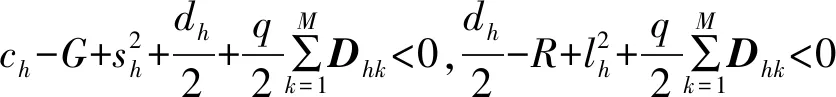
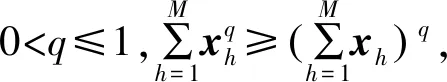
(14)

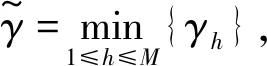
(15)

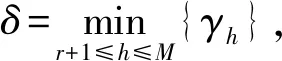
(16)

由引理1可以得到误差系统的平凡解是全局随机有限时间吸引的,并且:

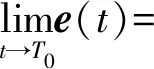
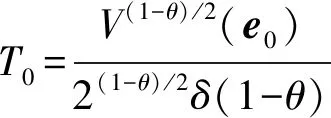
在文献[7-11]中,研究了多权值复杂网络的同步及其在公共交通领域的应用问题值得注意的是笔者的研究与文献[7-11]有许多不同之处。第一不同于文献[9-11],笔者可以估计出同步的时间,借助于复杂网络的有限时间同步,来研究城市公交网络的有限时间平衡问题,使得城市公交网络有限时间内实现平衡;第二将白噪声考虑到了城市公交网络,可以很好地描述城市公交网络中的随机干扰,例如由于车流量过大造成的交通拥堵等,使得模型更贴近实际;第三笔者的方法与文献[7-11]不同,笔者借助图论中的基尔霍夫矩阵树定理,间接构建全局李雅普诺夫函数,有效避免了直接构建全局李雅普诺夫函数的困难。

3 数值算例

城市公交网络作为典型的复杂网络,通过对其分析,可以得出城市公交网络具备NW小世界网络的特征。因为Chua系统是一个经典的带时滞的混沌系统,可以很好地刻画时滞对系统的影响,所以文中的顶点系统采用Chua系统。首先,考虑一个由20个顶点和两种权值构成的带时滞的随机城市公交网络,其中顶点表示公交线路,那么理想状态下运行的耦合公交线路可以表示为:

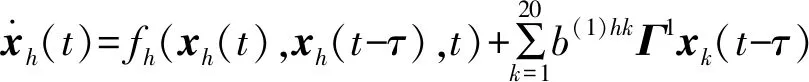
(17)

式中:xh=(xh1,xh2,xh3)T是三维的状态向量,代表第h条公交线路的运行状态,其初值是随机产生的:

fh(xh(t),xh(t-τ),t)=Cxh(t)+a1(xh(t))+a2(xh(t-τ))

其中:a1(xh(t))=(-0.5α(m1-m2)×(|xh1(t)+1|-|xh2(t)-1)|,0,0)T,

a2(xh(t-τ))=(0,0,-βνsin(ϑxh1(t-τ)))T,

C=(C1,C2,C3)T,C1=(-α(1+m2),α,0),

C2=(1,-1,1),C3=(0,-β,-ω),α=10,β=19.53,

ω=0.1636,m1=-1.432 5,m2=0.783 1,ν=0.5,

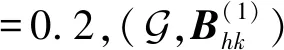
在系统(17)基础上,将考虑了随机扰动和合适的控制器的系统作为响应系统,其刻画了实际中运行的耦合公交线路,表达式为:

τ))-gh(t,xh(t),xh(t-τ))]d(t),h=1,2,…20

(18)

式中:yh(t)为三维的状态向量,代表第h条公交线路的运行状态,其初值是随机选取的。

因此假设A2是满足的,Γ1,Γ2是不同公交线路的内部耦合矩阵,其取值为:

控制器的表达为:

(19)

式中:R=0.02,G=0.2,θ=0.05。

图1是城市公交网络的拓扑结构,将客流量和线路长度作为两种权值的子图分别呈现在图1。

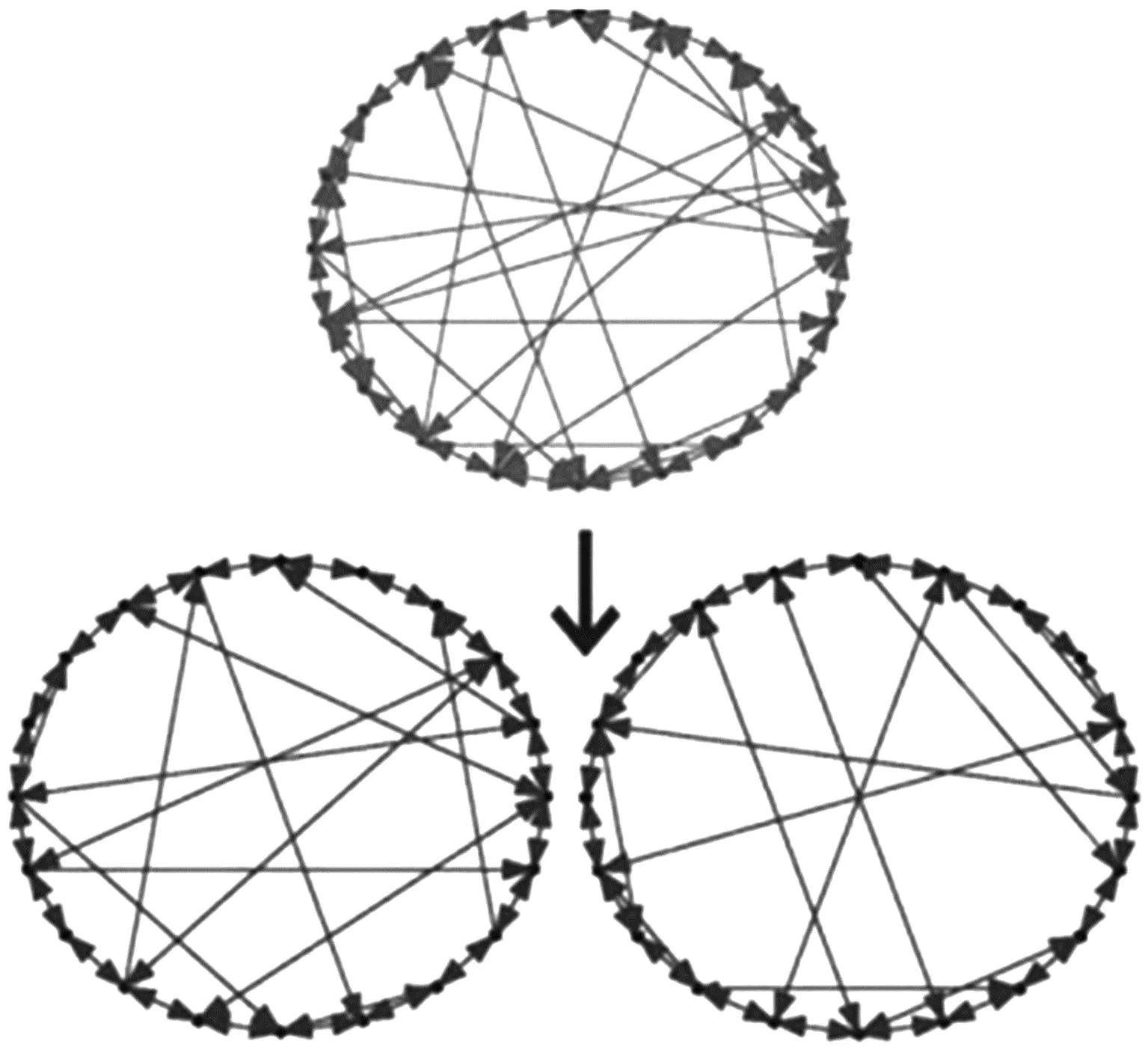
图1 城市公交网络

图2表示的是系统(17)和系统(18)的误差,从图2中可以很明显地看出,在t=1之后,误差系统的值趋于0(误差系统达到平衡),进一步验证了考虑随机扰动和时变的交通调度,实际运行的城市公交网络与理想状态下(平衡运行)的城市公交网络在有限时间内运行状态达到一致。

图2 系统(17)和系统(18)的同步误差, 其中τ= 0.02

4 结 论

借助复杂网络的知识,采用空间建模方法,将城市公交网络抽象为多权值的随机复杂网络模型。使用图论方法,间接构建全局李雅普诺夫函数,结合有限时间控制策略、稳定性理论以及随机分析的理论,借助复杂网络同步的概念,研究城市公交网络的有限时间平衡问题。即在实际运行的城市公交网络中考虑随机扰动(影响公交线路正常运行的随机因素)和合适的控制器(交通调度),通过交通调度,使得受到随机扰动后实际运行的城市公交网络,在有限时间内能与理想状态下的城市公交网络运行状态达到一致,即实际运行的城市公交网络实现平衡,进而公交车运行时的延误时间和乘客在公交线路上公交停靠站的等待时间均达到最短,最后通过数值算例验证了笔者所提出理论的可行性。

笔者只对影响公交线路运行的多种影响因素(多权值)做定性分析,没有考虑时变的多权值。在未来,将会尝试研究时变多权值下城市公交网络的有限时间平衡问题;另一方面,笔者研究的是合适地控制下城市公交网络的有限时间平衡问题,而周期间歇控制可以节约成本,节省人力物力的消耗,因此笔者也会尝试做周期间歇控制下的城市公交网络的有限时间平衡问题。