半潜钻井平台气隙频域分析

韦斯俊,梁园华,丁果林,孙政策

(中国船级社海洋工程技术中心,天津 300457)

半潜式钻井平台设计时,若初始静气隙太小,有可能会造成波浪砰击,影响平台安全;若初始静气隙太大,会导致平台过高,会增大平台的建造成本,并影响平台稳性。工程设计中采用基于势流理论的边界元方法和不规则波随机方法进行半潜式钻井平台气隙分析[1-3];在分析过程中需要关注平台二阶效应、波浪不对称和系泊系统等对气隙性能的影响,并采用模型试验对数值计算结果进行修正[4-7];对于平台运动具有强非线性的半潜式平台,还需采用非线性时域方法进行分析。在螺旋式的工程方案设计阶段,采用以上方法评估平台的气隙性能,需要耗费大量的时间和计算资源,影响方案设计进度。

为解决半潜式钻井平台设计过程中气隙分析的效率问题,找到影响平台气隙性能分析的关键因素,验证设计海况波浪参数对半潜式平台气隙性能的影响,对两座半潜钻井平台进行波浪绕射/辐射分析,基于线性气隙计算方法,利用Excel和VBA自主开发算法程序计算平台最小气隙值。预报半潜钻井平台在一系列不规则海况下的气隙,分析不规则波波浪能量与平台气隙的关系。同时,引入不对称因子来考虑波浪的不对称现象和非线性绕射现象,通过敏感性分析探讨不对称因子α对半潜钻井平台气隙的影响。

1 气隙计算原理

半潜钻井平台气隙计算分析采用频域分析方法,利用AQWA软件计算平台在波浪中的运动,得到平台重心处运动和各气隙观测点处的波面升高辐频响应传递函数,利用谱分析方法计算平台气隙观测点处垂向相对运动的最大值ZR,max,结合已知初始静气隙,计算得到最小气隙值。

1.1 垂向相对运动

平台气隙观测点处最小气隙值等于静气隙减去观测点垂向相对运动最大值,

AGmin=Z0-ZR,max

(1)

式中:AGmin为观测点最小气隙值;Z0为初始静气隙;ZR,max为观测点垂向相对运动最大值。

观测点垂向相对运动辐频响应传递函数ZR为复数,与平台重心处运动和波面升高有关,

ZR=ξ3-xiξ5+yiξ4-ξRD

(2)

式中:ξ3、ξ4、ξ5分别为平台重心处的垂荡、横摇和纵摇运动辐频响应传递函数;xi和yi为观测点的水平坐标;ξRD为观测点处包含波浪辐射和绕射成分的扰动波面升高。

由下式计算观测点垂向相对运动的辐频响应传递函数幅值ZR,RAO。

(3)

式中:R和I分别为复数的实部和虚部。

实际海况中波浪波峰和波谷是不对称的,所以在计算时引入不对称系数α进行修正,ZR表述为ZR=ξ3-xiξ5+yiξ4-α·ξRD,对应的辐频响应传递函数幅值ZR,RAO为

(4)

根据DNV-RP-C103[8],计算分析基于分布函数90%分位点时,不对称系数α取1.1。

1.2 谱分析

根据计算得到的ZR,RAO,结合已知的波浪谱Sζ(ω),可以计算得到观测点垂向相对运动的响应谱。

SR(ω)=|RAO|2Sζ(ω)

(5)

工程实践经验表明,观测点垂向相对运动的短期响应服从Rayleigh分布,分布函数如下。

(6)

式中:x为变量;σ,σ2为标准差和方差。可由响应谱SR(ω)得到。

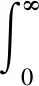
(7)

此外,可进一步求得短期响应的最大值。短期响应最大值与有义值的关系为

(8)

式中:pe对应不同的分布函数分位点;N可由短期预报时间和平均过零周期计算得到。

pe取90%,短期预报时长为3 h。

2 半潜钻井平台计算模型

对两座半潜钻井平台进行波浪绕射/辐射分析,半潜钻井平台湿表面网格见图1。

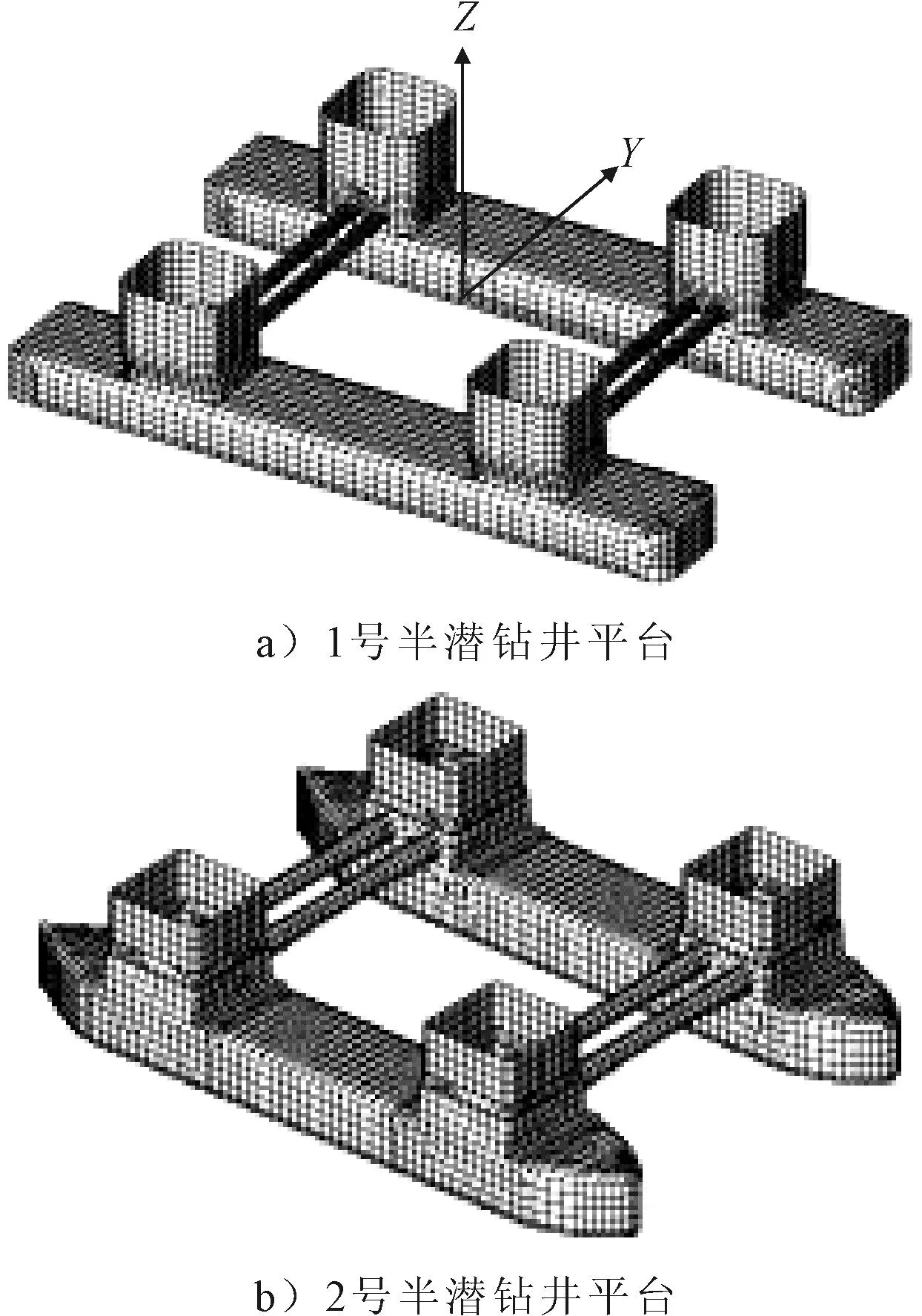
图1 半潜钻井平台湿表面网格

气隙分析时,考虑到半潜平台的对称性,选取的气隙观测点见图2,位于平台平面第2象限和第4象限,共17个气隙观测点。

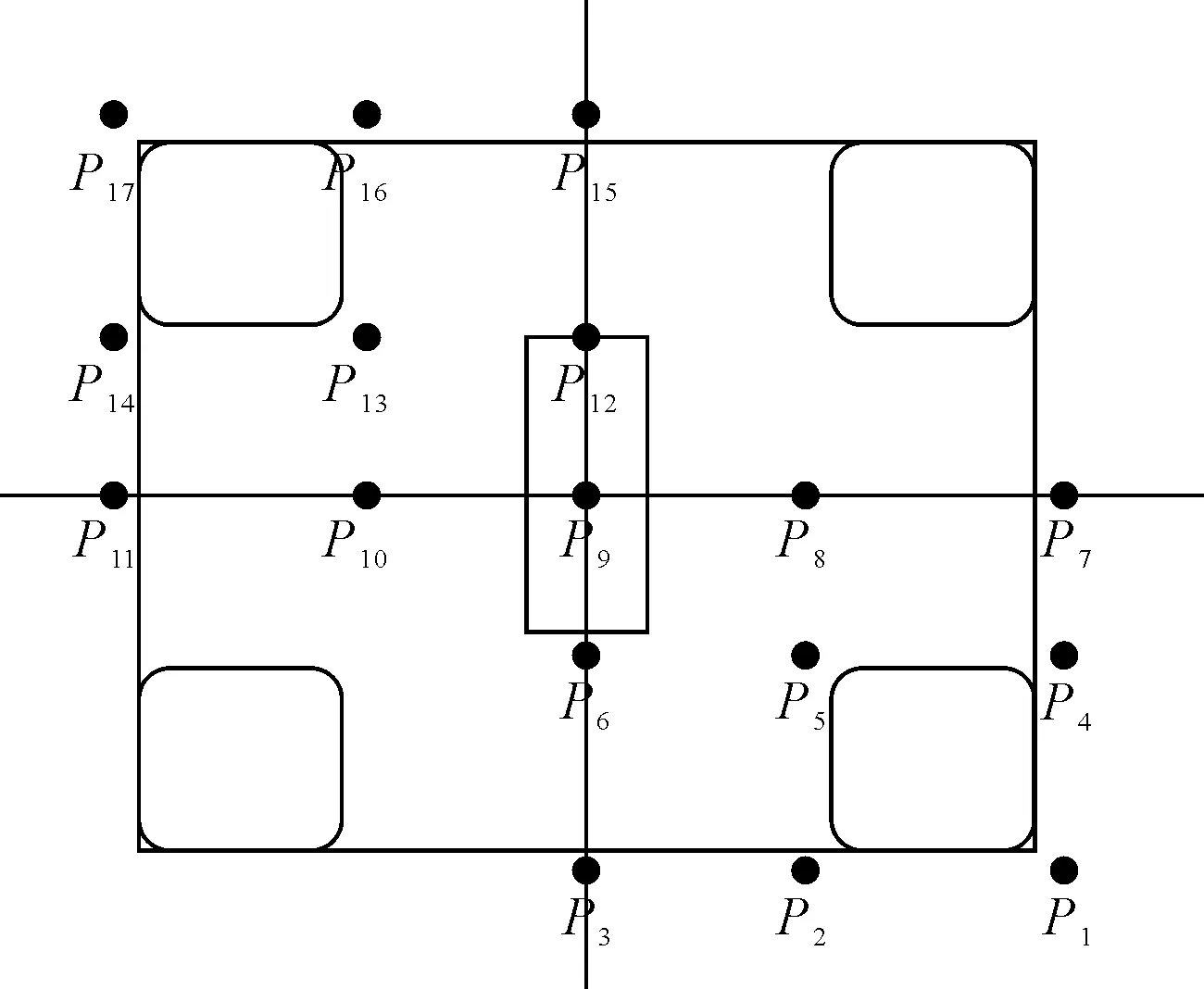
图2 半潜钻井平台气隙观测点

观测点包括了平台立柱和底部甲板的轮廓。平台立柱附近会产生局部波浪爬升和飞溅等非线性现象,基于线性势流理论的计算方法无法准确预报立柱附近的扰动波面升高,所以在选择气隙观测点时,观测点距离平台立柱的水平距离至少为0.2D,D为平台立柱的特征直径[9]。

1号平台的作业水深为1 500 m,2号平台作业水深为250 m。本次气隙分析只考虑半潜钻井平台自存工况,自存工况下1号平台和2号平台的初始静气隙均为14.00 m。自存工况的海况条件为:1号平台最大有义波高为13.7 m,过零周期为10.0 s;2号平台最大有义波高为17.3 m,过零周期为13.0 s。根据波陡、有义周期和过零周期关系确定用于气隙分析的海况条件,见表1。气隙分析时,取浪向角由0°到360°,间隔15°。

表1 海况条件

3 计算结果

3.1 扰动波面升高云图

1号半潜钻井平台在有义波高为13.70 m时的扰动波面升高云图见图3,2号半潜钻井平台在有义波高为17.30 m时的扰动波面升高云图见图4。由图4可知,在0°、30°、60°和90°等不同浪向,考虑了波浪绕射和辐射成分的扰动波面升高较大值都集中在平台立柱附近区域。

图3 1号平台扰动波面升高云图

图4 2号平台扰动波面升高云图

3.2 最小气隙计算结果

气隙分析时,对1号和2号半潜钻井平台计算18个海况,浪向角0°～360°(间隔15°),共432个工况。计算每个气隙观测点在各工况下的气隙值,从中筛选出每个观测点的最小气隙值,结果见图5。

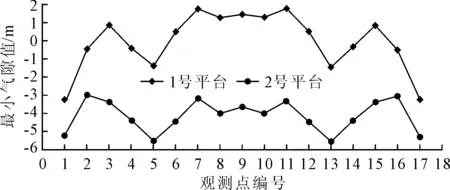
图5 半潜钻井平台最小气隙变化趋势对比

可以看到,自存工况下两座平台都会出现负气隙,1号平台最小气隙值-3.26 m,出现在P1点(P17,-3.22 m);2号平台最小气隙值-5.60 m,出现在P13点(P5,-5.55 m)。平台立柱周围8个观测点P1、P2、P4、P5、P13、P14、P15、P16的气隙值比其他区域的气隙值要小,气隙比较危险的点都是位于立柱附近的区域。

3.3 不规则波波浪能量对平台气隙的影响

3.3.1 气隙与不规则海况的关系

因为气隙观测点的最小气隙结果是对称的,所以选择第4象限的P1～P9的气隙结果作为分析对象,按照表1的海况条件,绘出每个观测点最小气隙随海况编号变化趋势,见图6。可以看到,出现危险气隙的海况不一定是有义波高较大的海况。

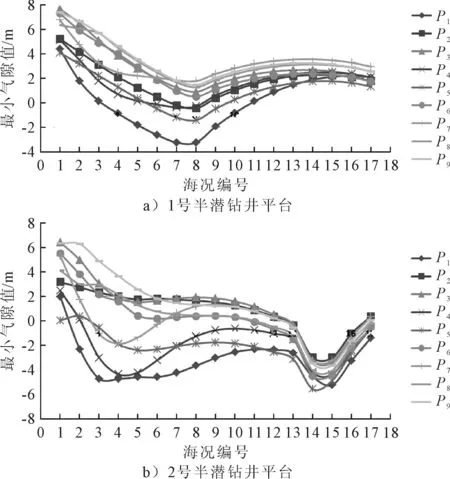
图6 半潜钻井平台各观测点最小气隙随海况变化趋势

由图6a)1号平台结果可知:①对于海况1～7,波陡一样时,有义波高越大,最小气隙值越小,即观测点垂向相对运动越大;②对于海况8～17,有义波高一样时,波陡越大,最小气隙值越小,即观测点垂向相对运动越大;③有义波高越大,最小气隙值不一定越小,较小的有义波高也可能出现较危险的气隙,例如P1、P4、P5观测点海况3和海况12、海况5和海况10的结果对比。

由图6b)2号平台结果可知:①有义波高越大,最小气隙值不一定越小,较小的有义波高也可能出现较危险的气隙,例如P1、P4观测点的海况3、4的最小气隙小于海况16、17;②如果有义波高相同的前提条件不成立,最小气隙值(观测点垂向相对运动)不随波陡值变化呈正(负)相关关系。

3.3.2 结果分析

以1号平台为研究对象对以上气隙与不规则海况的关系进行研究分析。选取海况6至12,绘出波浪谱密度曲线,见图7,计算出各海况波浪谱密度曲线包络面积,见表2,谱密度曲线包络面积表示波浪谱能量。

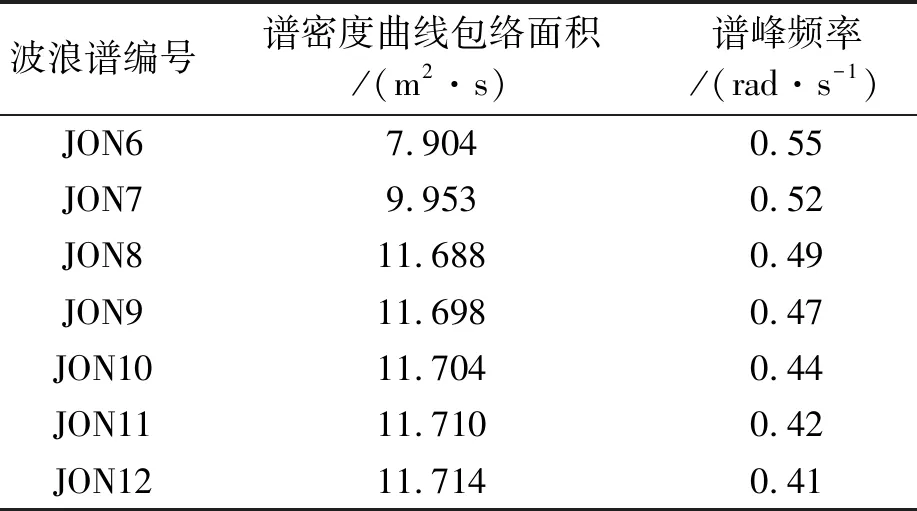
表2 1号平台海况6至12波浪谱密度曲线包络面积

可以看到,海况8～12,在有义波高一样的情况下,谱密度曲线包络面积基本是一样的,都是11.7;但是,波陡越小,谱密度曲线峰值越大,曲线的形状更为“尖瘦”,谱峰密度越小,由0.49 rad/s逐渐递减到0.41 rad/s。另外,海况6和7的谱密度曲线包络面积要小于海况8～12,谱峰频率分别为0.52和0.55 rad/s。

图6中各观测点最小气隙随海况的变化趋势基本是一致的,选取P1点作为研究对象。绘出P1点的垂向相对运动RAO曲线,见图8。可以看到P1点各角度的RAO曲线在0.2～0.5 rad/s频率范围内重合度高,且变化趋势一致:在0.30 rad/s出现峰值,在0.35～0.45 rad/s出现谷值。

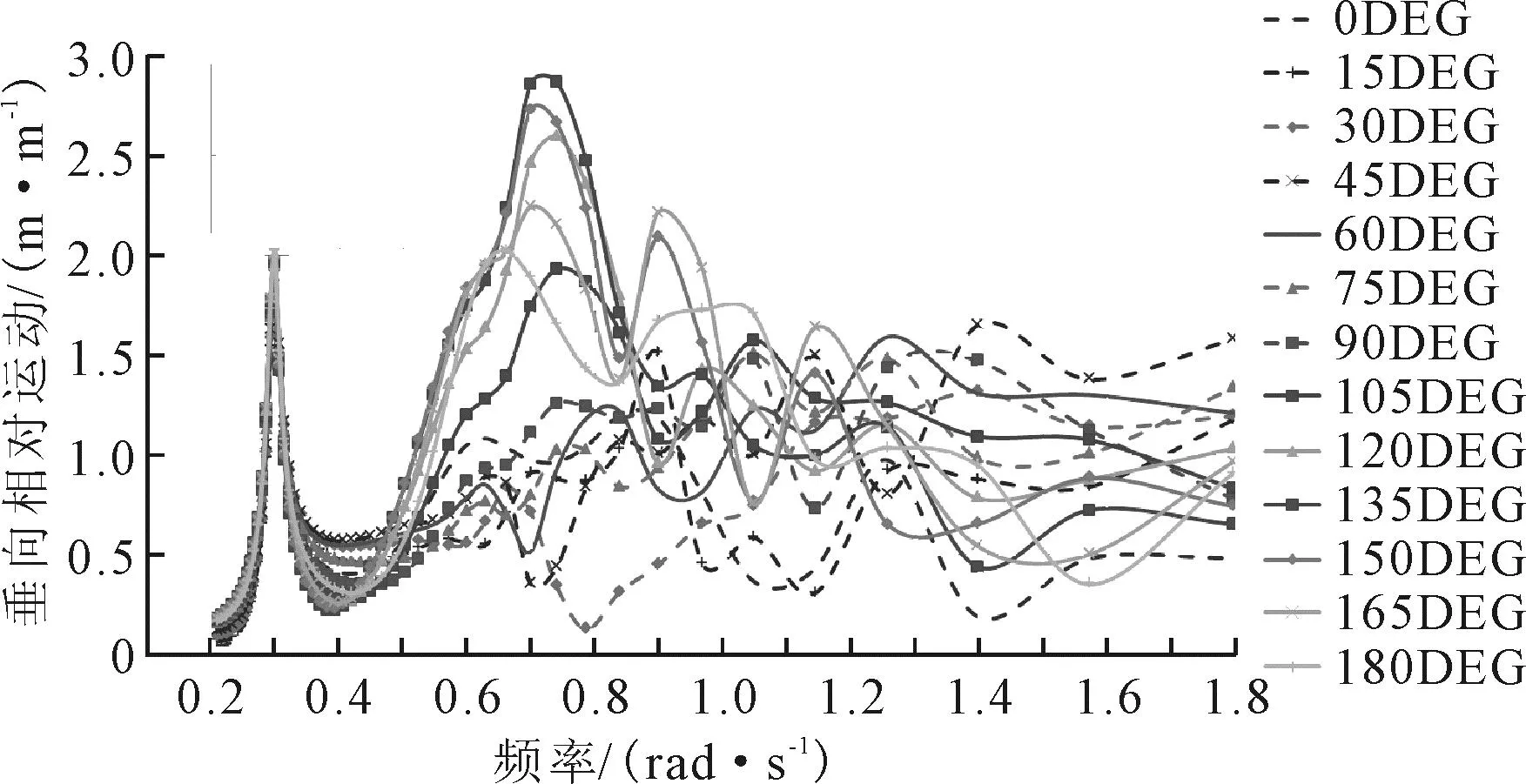
图8 1号平台P1点垂向相对运动RAO

为了更清晰地解释该现象,选取P1点气隙值最小的浪向对应的RAO作为分析对象,见图9。

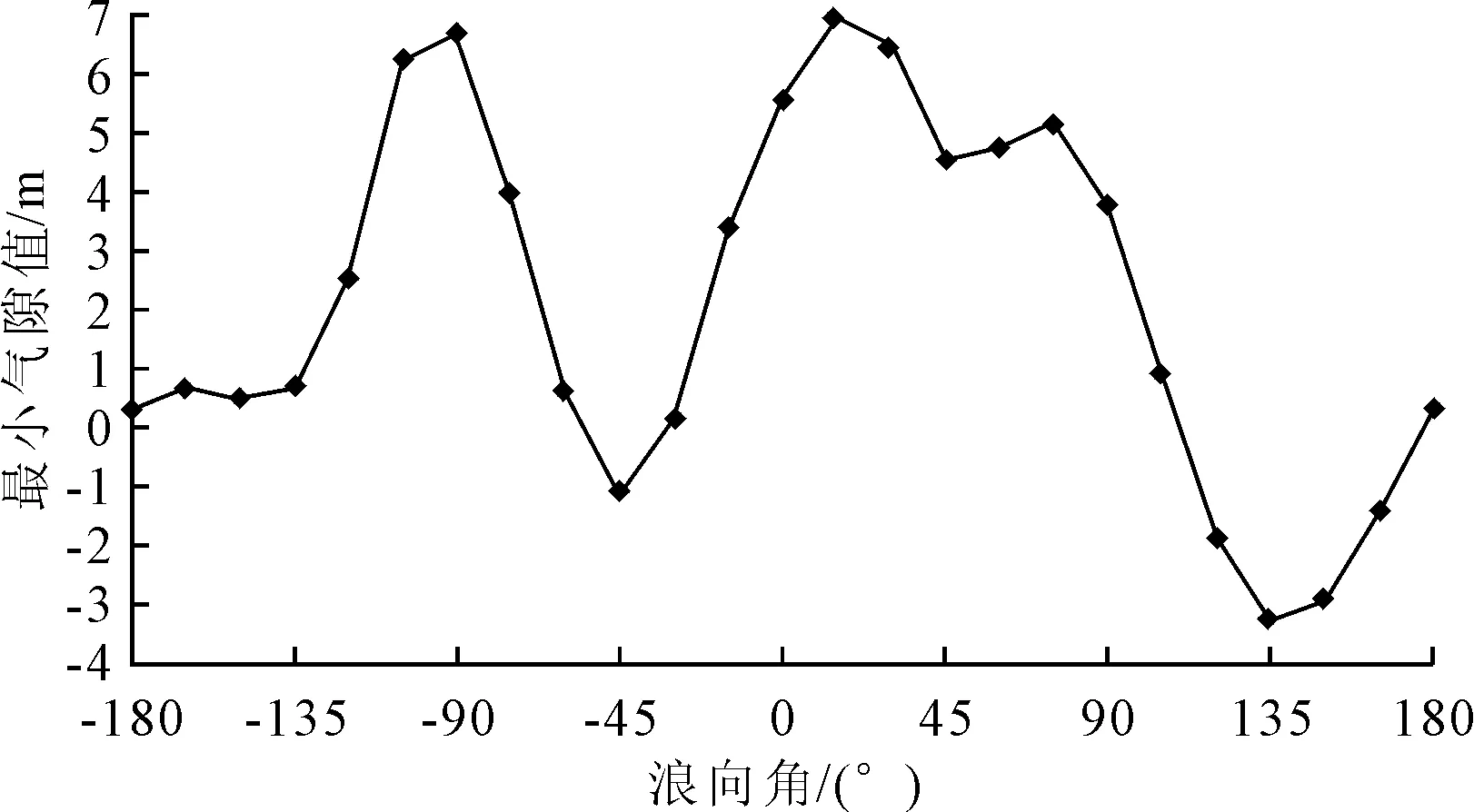
图9 海况7中观测点P1各浪向最小气隙值

由图9可知:P1点最小气隙值为-3.26 m,对应的浪向角为135°,所以选取图8中135°浪向的垂向相对运动RAO曲线为分析对象,见图10。

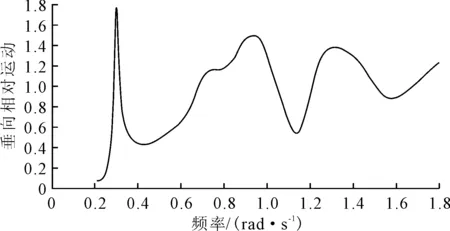
图10 135°浪向P1观测点垂向相对运动RAO

利用图7和图10,得到P1点的垂向相对运动响应谱,见图11,响应谱曲线包络面积见表3。

表3 P1观测点垂向相对运动响应谱包络面积

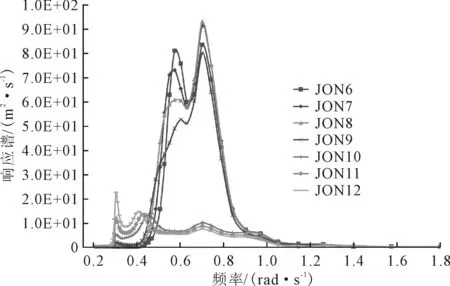
图11 135°浪向P1观测点垂向相对运动响应谱

可以看到,海况6、7、8、9对应的响应谱面积要明显大于海况10、11、12,海况7、8的谱密度曲线面积最大,二者值相差不大,稍大于海况6、9,这与图6a)中P1点最小气隙随海况变化趋势结果一致。

图10中的RAO曲线在0.30 rad/s为峰值,在0.40 rad/s为谷值,由表2和图7知海况10、11、12的谱峰频率都在0.40 rad/s附近,即波浪谱能量集中的频率对应P1点垂向相对运动响应RAO的谷值,其他海况的谱峰频率在0.47～0.55 rad/s,波浪谱能量不集中于P1点垂向相对运动响应RAO的谷值区域,所以海况10、11、12计算得到的P1点垂向相对运动的响应应该小于海况6、7、8、9。

以上分析表明,对于半潜式钻井平台,最危险气隙不一定出现在有义波高最大的海况;即使海况有义波高较小,若该海况的波浪能量集中于气隙观测点垂向相对运动共振区域,也会发生危险气隙。

3.4 不对称因子α的影响

式(4)中引入不对称因子α来考虑实际波浪的不对称现象和非线性绕射现象。为分析不对称因子对平台气隙计算结果的影响,对不对称因子α进行敏感性分析,计算α取值为1.00、1.05、1.10、1.15、1.20时,两座平台各观测点的最小气隙值计算结果见表4、5。

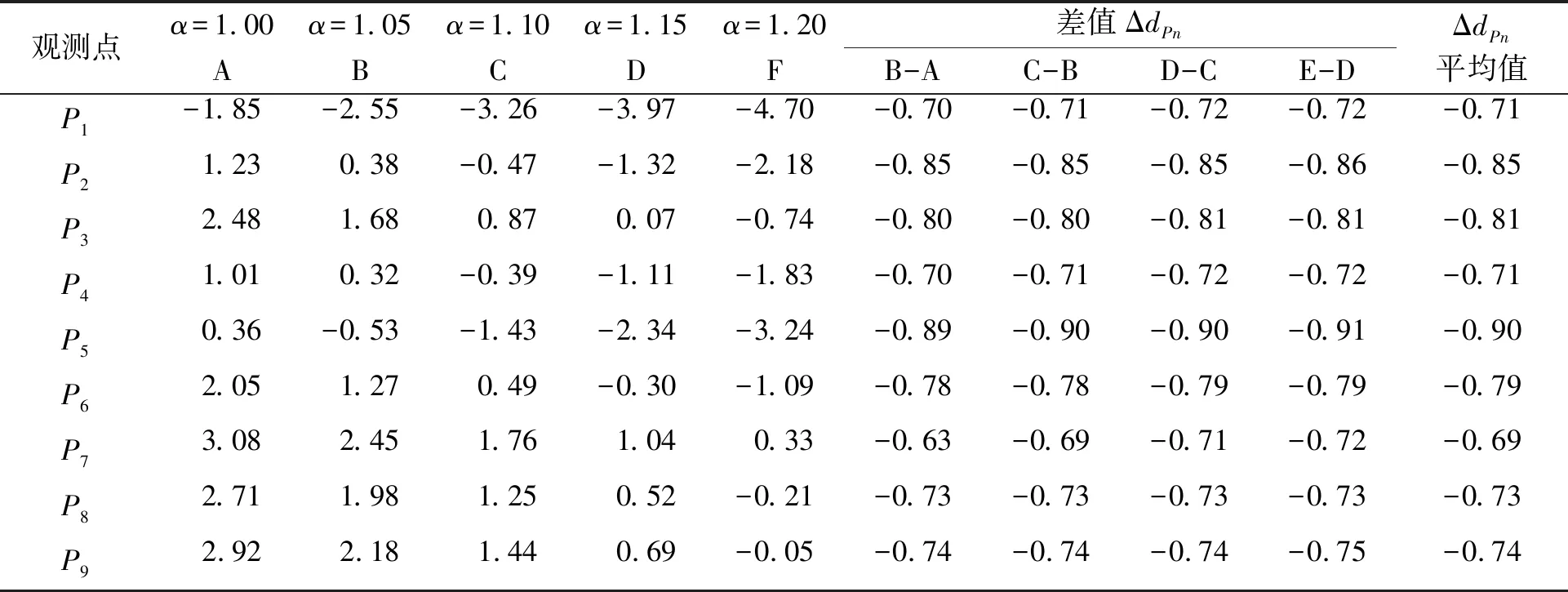
表4 1号平台不对称因子敏感性分析

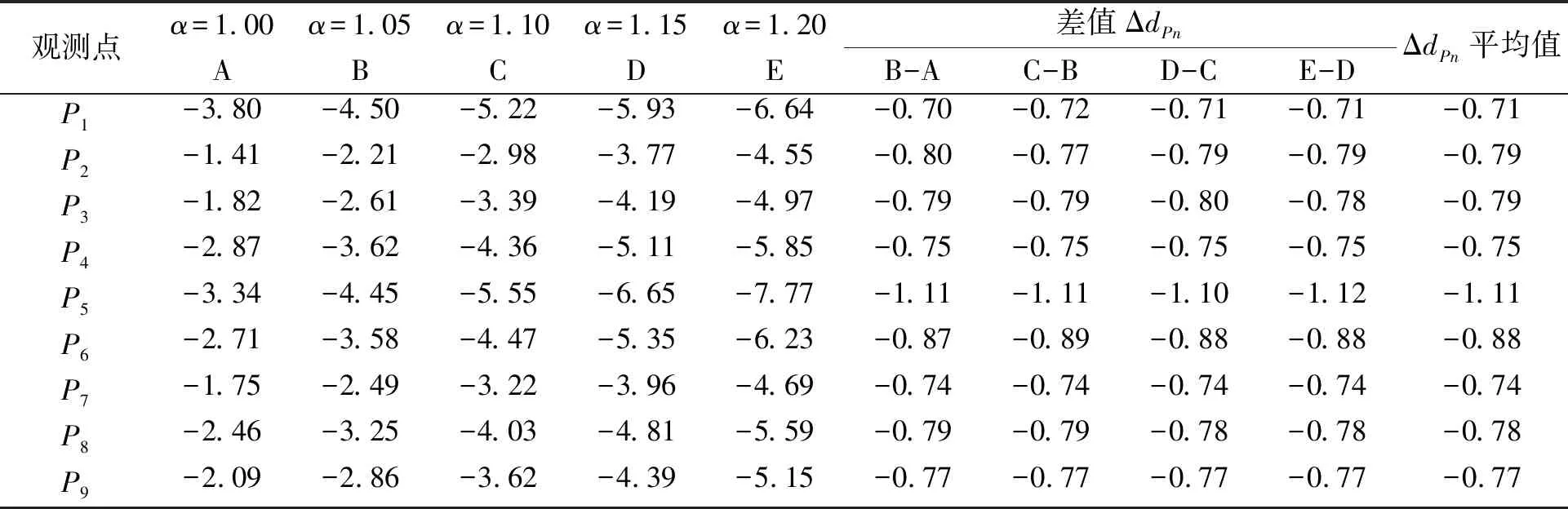
表5 2号平台不对称因子敏感性分析

由计算结果可以看到,观测点的最小气隙值随α增大而减小,α每增大0.05,观测点Pn最小气隙值都相应的减小一固定值ΔdPn。例如,对于1号平台,P1观测点ΔdP1=0.71,P2观测点ΔdP2=0.85,P5观测点ΔdP5=0.90,P6观测点ΔdP6=0.79;对于2号平台,P1观测点ΔdP1=0.71,P2观测点ΔdP2=0.79,P5观测点ΔdP5=1.11,P6观测点ΔdP6=0.88。由此可知,引入不对称因子α考虑波浪的不对称现象和非线性绕射现象,计算得到的气隙值更危险,每个观测点的最小气隙随不对称因子α呈负相关关系,且最小气隙随α的变化为定值。

4 结论

1)两座半潜钻井平台在自存工况下都会出现负气隙,平台立柱附近产生负气隙比其他区域更为严重。

2)一系列不规则海况中两座半潜钻井平台气隙结果表明,平台最危险气隙不一定出现在有义波高最大的海况,当不规则波波浪能量集中在平台垂向相对运动共振周期区域时,在有义波高较小的海况也会出现危险气隙。

3)通过不对称因子α敏感性分析发现,观测点的最小气隙与不对称因子α呈现负相关关系,考虑不对称因子会使得平台的气隙结果更为危险。