基于改进的K-means聚类和深度神经网络的轴承故障诊断算法研究
2023-12-26孟洪颜胡玉坤王艳春
孟洪颜,胡玉坤,冯 双,周 冬,王艳春,*
(1.齐齐哈尔大学 通信与电子工程学院,黑龙江 齐齐哈尔 161006;2.黑龙江大学 电子工程学院,哈尔滨 150080;3.朝阳师范高等专科学校,辽宁 朝阳 122600;4.齐重数控装备股份有限公司电控设计部,黑龙江 齐齐哈尔 161005)
0 引 言
滚动轴承作为机械工业的关键基础部件,广泛应用于航空航天、冶金、电力汽车工业、数控机床等领域。滚动轴承是旋转机械中容易发生故障的零部件之一[1]。在工业物联网大型机械的故障中,轴承缺陷占比达40%;在小型机械故障中,轴承缺陷的占比为90%[2]。滚动轴承一般由内圈、外圈、滚动体和保持架组成,当出现部分损坏或缺陷时,轻则设备产生噪声、振动异常,重则导致故障停机,影响生产,造成财产和经济损失,因此对于旋转机械的轴承进行及时的监测和故障诊断至关重要[3]。
依据数据是否有标签,机器学习的方式可分为有监督学习和无监督学习。有监督学习方法在训练模型时需要特征数据和数据所对应的标签。而无监督学习方法只需要特征数据,不再需要与之对应的标签,省去了大量人工标注的工作[4-5]。聚类算法是无监督学习中常用的算法,已有研究采用K-means及改进的K-means聚类算法进行轴承故障诊断的模式识别,在此基础上进行神经网络的无监督学习或半监督学习。文献[6-7]介绍了采用K-means方法从振动信号中学习特征,用来降低特征参数的空间维数。文献[8-10]研究的高速列车或旋转部件的轴承,采用不同的信号特征提取方法。文献[11-13]针对轴承振动数据量大,K-means聚类的局限,分别提出了Bi-K-Mean聚类算法、基于Spark的并行蚁群优化(ACO)-K-Means聚类算法、K-means++的无监督学习机制和改进的混合遗传算法K 值聚类,提高聚类的效率,并用于轴承系统的诊断。文献[14]从轴承振动信号提取时频域信号,用K-means聚类算法定义不同的退化状态,建立卷积神经网络识别模型。文献[15]采用自编码器结构进行特征提取,将距离度量学习和K-means聚类方法集成到无监督学习神经网络结构中,该方法不仅在标记数据较少的半监督学习任务中取得了良好的诊断性能,而且适用于纯无监督学习问题。文献[16]针对从原始数据中提取的特征值,使用K-means算法获取标签,将原始振动数据转换为小正方形图像,送入到设计的CNN神经网络模型中进行旋转系统的磨损水平分类和诊断。虽然上述和K-means有关的算法已用于轴承的故障的模式识别,但相关的K-means算法实现复杂或收敛不佳。
针对上述问题,考虑到实际工作场景中,面对轴承振动数据量大,占用资源较多等问题,提出基于改进的K-means聚类和深度神经网络的轴承故障诊断算法,针对K-means采用随机初始化聚类中心,易造成故障类别间重叠、分类随机的缺点。拟采用抽取小样本分层聚类,采用滤波和统计密度的方法找出簇的中心点,进行初始化中心的K-means聚类。同时,建立基于聚类伪标签的深度神经网络滚动轴承故障诊断的模型,使用具有伪标签的新数据集对模型进行训练和优化;使用常用的聚类评价指标和加入噪声的方法,研究了提出算法的聚类性能和模型的准确性、稳定性。
1 方法介绍
1.1 K-means聚类算法
K均值聚类算法是 Macqueen 在 1976 年提出的一种无监督学习方法[4,17],该算法需要随机生成或指定k个中心点,可通过对数据的迭代计算找出聚类中心,依据样本间的相似性将样本聚集到k个簇中,简单高效地找出簇与簇的中心。
算法的基本流程如下:
1)设样本X= (x1,x2,…,xn),每个样本有m个维度的特征,Xi=(x1,x2,…,xm),样本为n*m的矩阵。随机选取(指定)k个样本数据,得到初始聚类中心集C= {c1,c2,…,ck} 。
2)计算每个样本到每个初始聚类中心的欧氏距离:
(1)
式中:xi为第i个样本 (1≤i≤n);cj为第j个簇中心,1≤j≤k;xit为第i个样本的第t个特征,1≤t≤m;cjt为第j个簇中心的第t个特征。
3)按照样本到簇中心距离的大小分配到距离最近的簇中心所在的簇内,得到k个簇{C1,C2,…,Ck} 。
重新计算簇的中心点,中心点坐标就是簇内所有样本的各维度的均值,计算公式为
(2)
式中:cl为第l个聚类中心,1≤l≤k;|Cl|为第l个类簇中样本的个数;xi为第l个簇中第i个样本,1≤i≤Cl。
4)重复步骤2)和步骤3),直至类中簇的中心无变化或达到指定迭代次数。
1.2 改进的K-means聚类算法
K-means聚类算法是一种典型的无监督机器学习方法,但在对滚动轴承振动数据进行聚类时,发现聚类中心随机、故障类别重叠等问题。针对上述问题,提出随机从样本中抽取5%的小样本进行分层聚类,对簇中的数据进行滤波操作,滤除簇的边缘点,统计滤波后每个簇的数据的密度,选取密度最大的点为K-means聚类的初始中心点,然后按照1.1节中K-means聚类算法进行数据聚类。改进的K-means算法的流程如下:
1)输入样本集D={x1,x2,…,xm};簇数为k。
2)初始化每个样本为1簇,Cj={xj,j∈{1,2,…,m}},计算两个点的欧氏距离d(Ci,Cj),得到距离矩阵M。
3)如果当前簇个数q大于k时,找出距离矩阵中最近的两个簇Ci*和Cj*,将两者进行合并Ci*=Ci*∪Cj*,将j*后面的簇的序号j=j*+1,并进行更新。
4)删除距离矩阵M中的j*行和j*列,重新计算Ci*到其它簇的距离,更新距离矩阵M。
5)将q=q-1,循环步骤3)~步骤5),直到q=k,返回样本簇的划分集合C={C1,C2,…,Ck}。
6)对每一个簇Ci∈{C1,C2,…,Ck},计算簇内两个点的欧氏距离d(xi,xj),其中{xi∈Ci,xj∈Ci;i≠j},得到距离矩阵M。
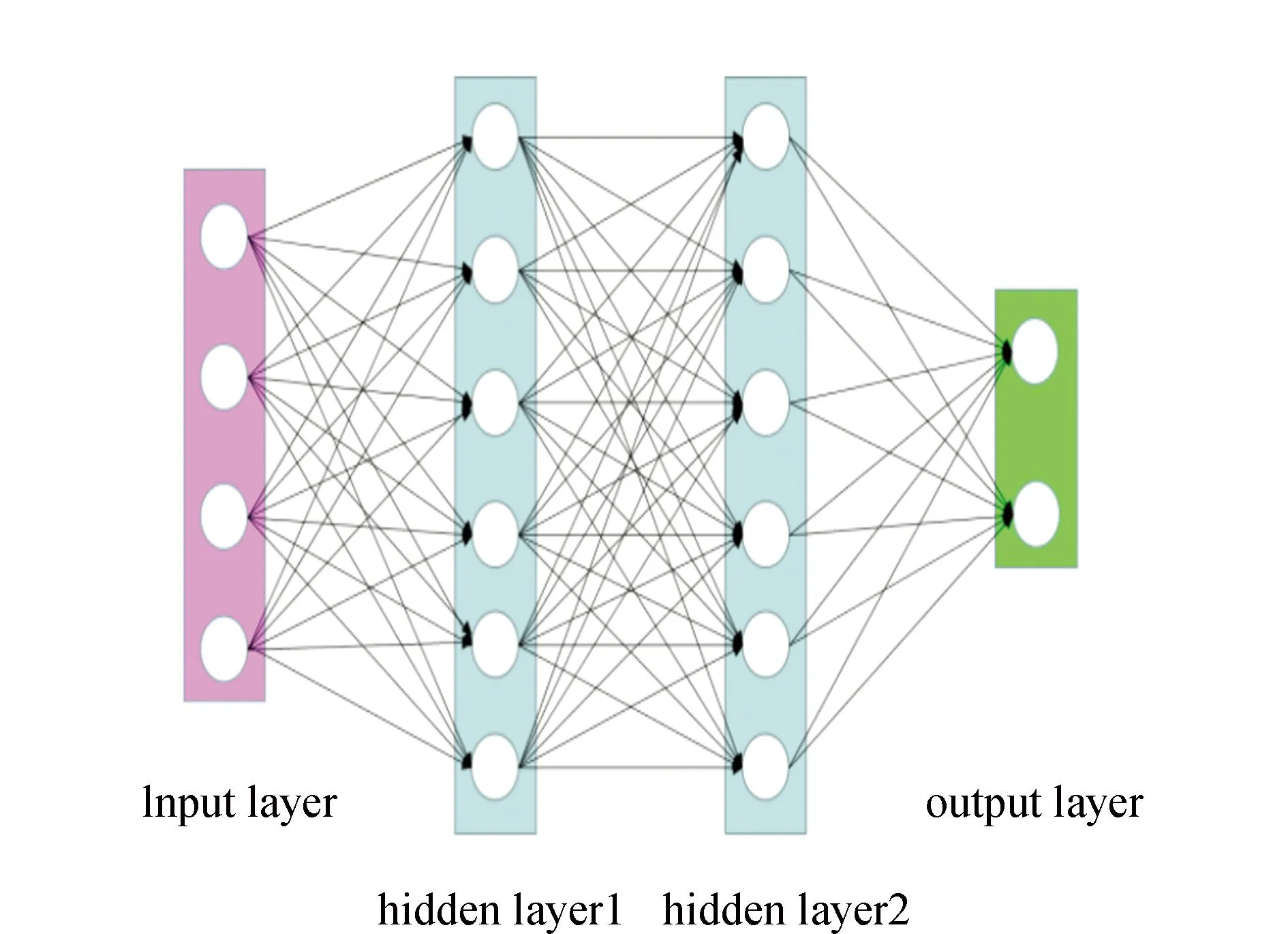
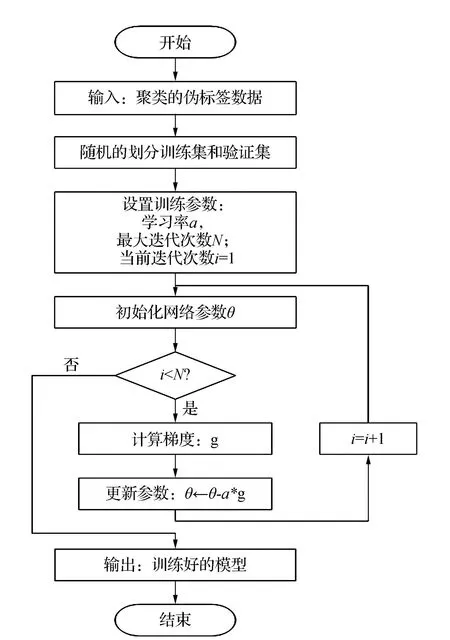
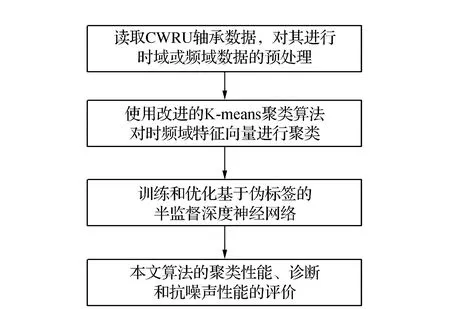
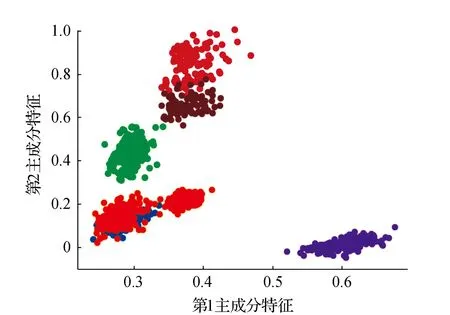
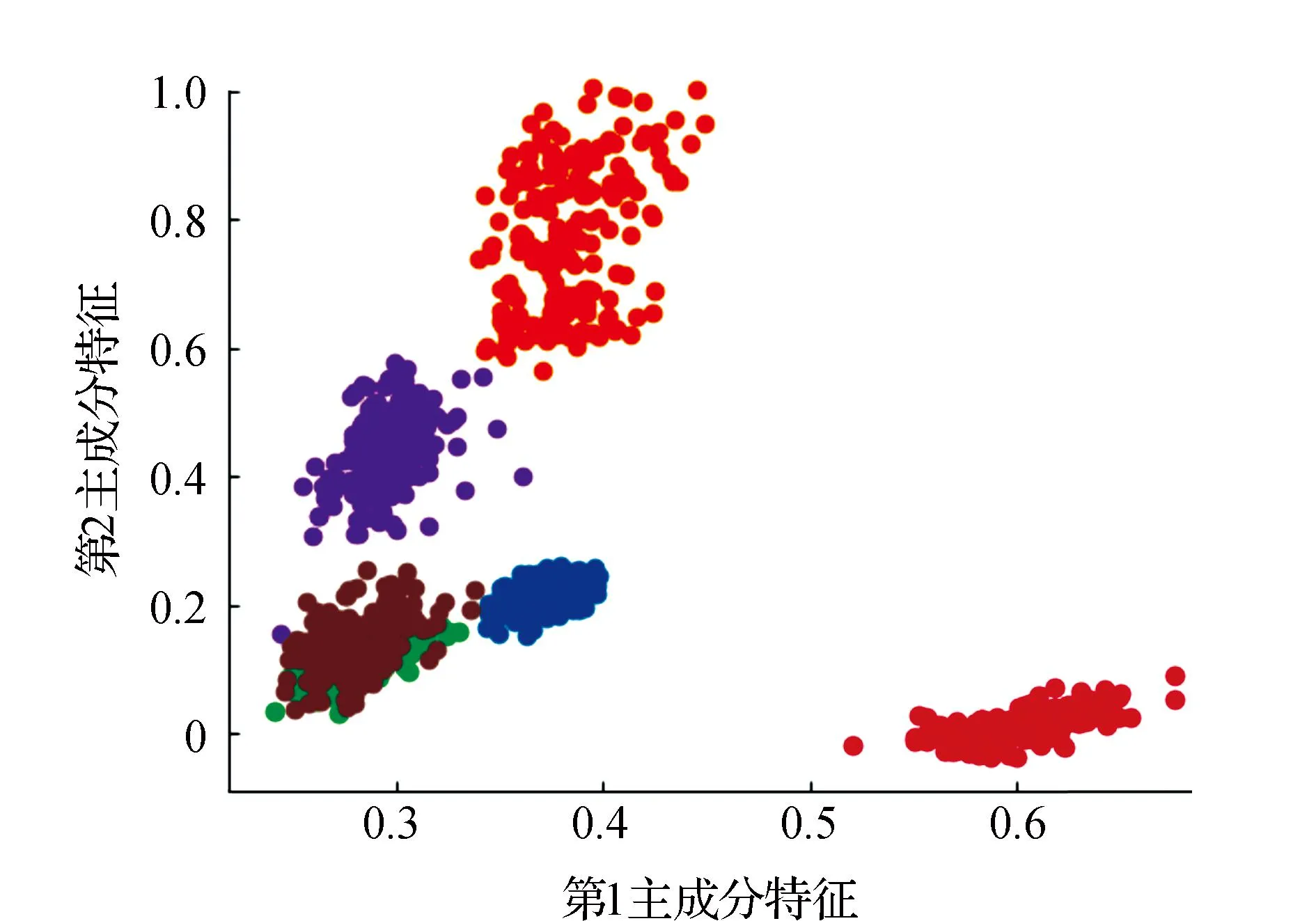
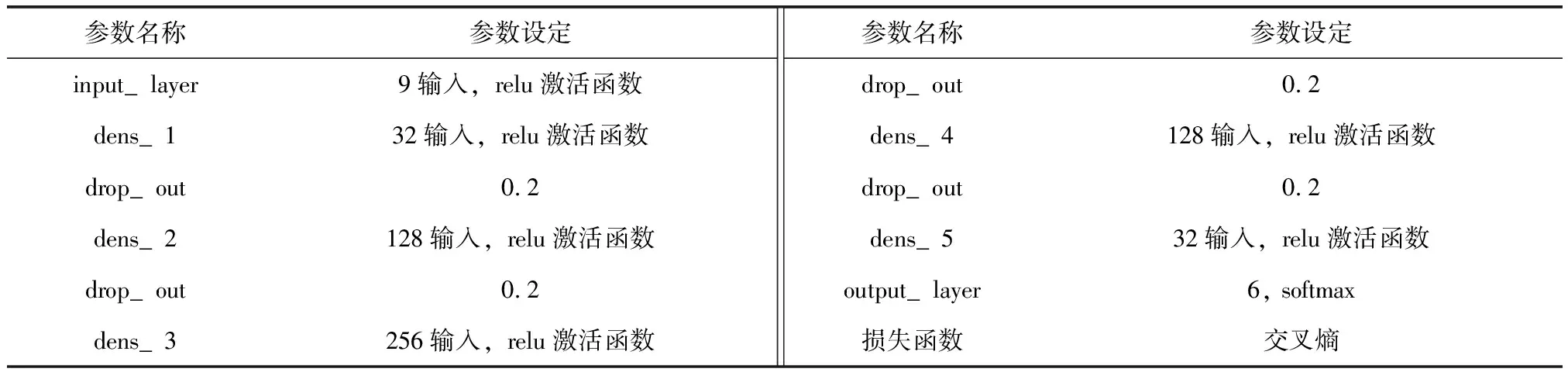
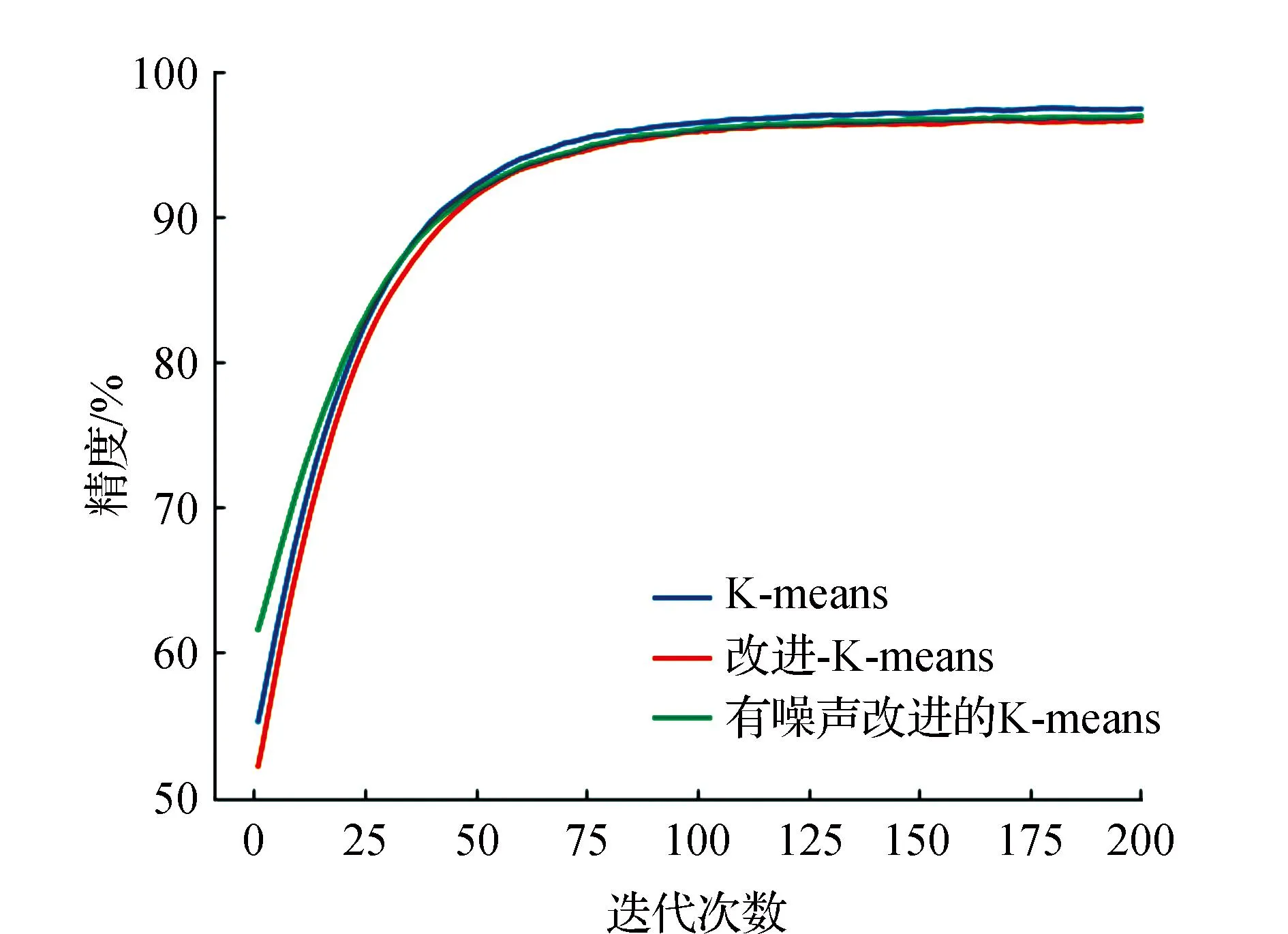
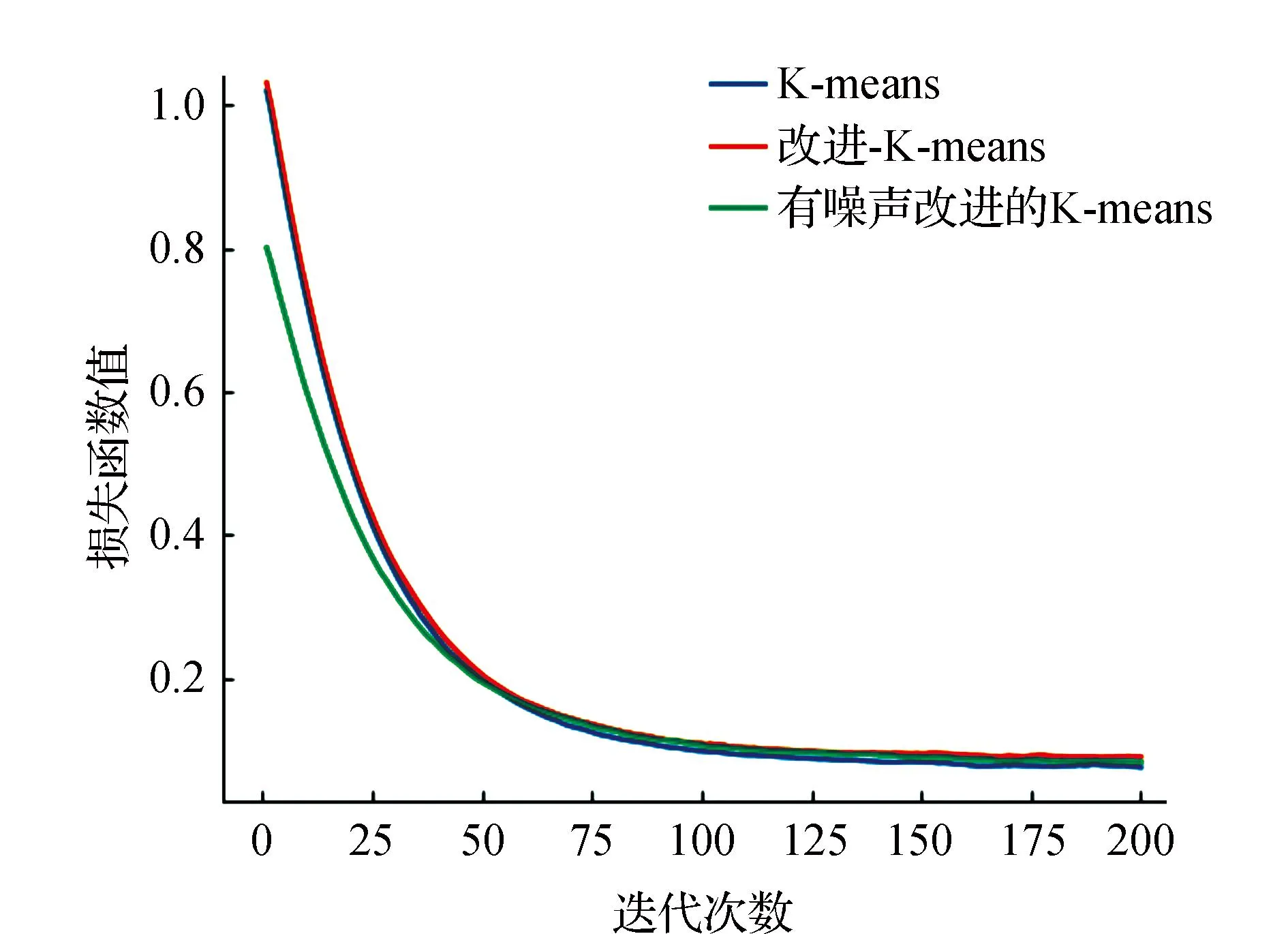
7)获取簇Ci类内最大距离di_max,设置过滤的半径Ri=0.2*d_max,统计d(xi,xj) 8)获取簇Ci的ρi中最大的密度ρimax,对应的样本即是簇的中心点xip。 9)依次获取所有簇的中心点,创建Points={x1p,x2p,…,xkp}。 10)初始化K-means聚类算法的中心点为Points,执行1.1中的2)~4)直到聚类完成。 通过观察上述的算法流程,可得:步骤1)~步骤5)实现小样本的分层聚类功能,步骤6)和步骤7)实现簇的滤波,滤除簇的边缘噪声点。步骤8)~步骤10)实现初始化中心的K-means聚类,返回样本的所有分类,簇的序号即是数据集的伪标签,伪标签可进行基于伪标签的半监督学习的深度神经网络建模。 深度神经网络(Deep Neural Network,DNN)与神经网络区别在于:包含多个隐含层,网络变深,具有强大的学习能力,能够学习数据深层次的特征。1986年,Hinton G E提出了反向传播算法(Back propagation)[18],解决了多层感知机的复杂计算问题,为后来提出的各种深度神经网络的研究和发展给出了理论指导和计算公式。深度神经网络的基本结构见图1。包含输入层、2个隐含层和输出层,每层之间通过全连接的方式连接,隐含层的层数可根据实际需要设计。 图1 神经网络结构Fig.1 Neural network structure diagram 由图1可见,多层神经网络模型,其中包括:输入层X={x1,x2,…,xn};隐含层Y={y1,y2,…,yn};输出层O={o1,o2,…,ol};隐含层与输出层之间的权重W={w1,w2,…,wj,…,wl}。深度神经网络工作中的前馈网络和方向传播原理为 1)前馈网络 对于隐含层,各隐含层神经元输出yj有: (3) 对于输出层,各个输出层神经元ok有: (4) 式(3)、式(4)中,神经元的激活函数f(·)根据应用的需要可选择Relu函数,Tanh函数和Sigmoid函数等,共同构成了多层神经网络的前馈网络的模型。 2)反向传播 当神经网络的输出结果O与实际结果D存在误差,误差的定义为 (5) 由式(5)可知,神经网络的输出误差E是关于各层的权值的函数,因此可通过调整各层权值来改变误差E的大小。采用梯度下降的方式对w和v进行求解,即求得w和v使得误差E最小。 (6) (7) 其中,η为学习率,j=0,1,2,…,n;k=1,2,3,…,l;i=0,1,2,…,n。 提出了基于伪标签的半监督深度神经网模型,训练该模型使用的是1.3节中提出的改进K-means聚类算法得到的伪标签数据,用训练好的的神经网络模型进行无标签验证集分类,将调优后的网络模型用于滚动轴承的故障诊断。基于伪标签的半监督深度神经网络训练流程见图2。 图2 半监督学习的深度神经网络程序训练流程Fig.2 Deep Neural network training flowchart for semi-supervised learning 技术路线是建立在改进的K-means聚类算法和基于伪标签的半监督深度神经网络算法研究之上,主要包括:数据的预处理模块、改进的K-means聚类算法模块、基于伪标签的半监督深度神经网络算法模块和算法的评价4个部分,见图3。 图3 技术路线的流程Fig.3 Flow chart of the technical route 数据来源于美国凯斯西储大学提供的标准的轴承测试数据(CWRU Bearing Data Center)[17]。对CWRU轴承数据进行预处理,包括:读取CWRU轴承数据,选取6种典型的故障,每种故障建立400*300维的数据向量,对上述数据向量进行时域和频域的信号处理,得到28维特征向量;利用改进的K-means聚类算法处理特征向量,得到特征向量的伪标签,建立特征向量和伪标签相对应的新数据集;用具有伪标签的数据集训练基于伪标签的半监督深度神经网络,训练并优化该神经网络;通过向特征向量中加入噪声,研究算法的聚类效果和抗噪声的性能。 仿真实验数据取自美国凯斯西储大学提供的标准的轴承测试数据[17]。选取的是SKF60205轴承,在转速1 797 r·min-1(约30 r·s-1)时,对正常、滚动体故障、内圈故障、外圈3点钟故障、外圈6点钟故障、外圈12点钟故障的6种轴承振动信号进行分析。故障直径为0.007英寸,数据采集的频率为12 kHz。轴承旋转一圈约采样12 kHz/30 r·s-1=400个数据,可作为有故障的一个周期公共的长度,实验中6类故障数据的读取最大长度为120 000个数据,每一类可将数据截取为400*300的数据集合。 轴承的振动数据是一维的时序信号,采用时域信号处理的方法获16个时域特征指标,再将信号变换到频域,得到12个频域指标[17,19]。16个时域特征指标(F1~F16)具体包括:平均值、绝对均值、最大值、最小值、峰峰值、方根幅值、平方均方根、方差、标准差、偏度、峭度、波形因子、裕度因子、脉冲因子、峰值因子、变异指数。时域特征中平均值、均方根值的稳定性好,对早期故障不敏感;峭度、峰值、裕度因子和脉冲因子对故障比较敏感,但稳定性差。12个频域指标(F17~F28)包括:平均能量、重心频率、均方频率、频率方差、均方根频率、幅值方差、幅值偏度指标、幅值峭度指标、频率标准差、频率歪度、频率峭度、平方根比率。频域特征中平均能量反应了振动能量的大小,重心频率、均方频率、频率方差反应了主频带的位置,最后的8特征反应了频谱的集中程度。由此可见,提取的时域和频域的信号代表了信号的不同的特征,由此也可反向推断出故障的类型。提取时域、频域指标参数见表1。 表1 时域频域指标 分别使用K-means算法和改进的K-means算法对表1中的特征数据进行聚类,并加入噪声后的数据再次进行改进K-means聚类。K均值算法的运算中,聚类结果与初始化的簇中心有关,而类内距离(Within Cluster Distance,WC)和类间距离(Between Cluster Distance,BC)是评价聚类效果的评价标准,同时总体的衡量聚类模型的优劣指标score,给出三者的计算公式[20]。聚类算法中,WC越小越好,相反BC越大越好,score越大越好。三者的实验结果见表2,对比可知K-means的聚类效果更好,改进的K-means次之,有噪声的最差。其降维可视化后的结果见图4、图5和图6。 表2 两种聚类结果评价 图4 真实标签的聚类Fig.4 Clustering of true labels 图5 K-means聚类Fig.5 K-means clustering 图6 改进的K-means聚类Fig.6 Improved K - means clustering (8) (9) (10) 由图4、图5和图6对比可见,K-means聚类将原本属于一类的分成了两类,将原本属于两类的分成了一类,相比之下提出的改进K-means聚类算法较好的区分出了所有的类别,改进的K-means算法分类效果优于K-means算法。 深度神经网络模型采用的多层全连接的神经网络模型,包括1个输入层,5个全连接的隐含层、4个drop_out层和1个输出成,drop_out层的设置是为了防止模型的过拟合,丢弃率设置为0.2。其结构见表3。输入的数据是经过PCA降维后的前9个维度,每1个隐含单元(包括全连接层和drop_out)可视为一个特征提取单元,输出层的输出是每种故障的概率。 表3 神经网络模型参数 对比图7和图8的数据可见,输入为有噪声数据的改进K-means网络模型收敛速度最快,3种模型在训练集上的精度均达到98%,并保持稳定,说明改进K-means聚类深度神经网络故障诊断模型收敛速度快、精度高、具有较好的鲁棒性。 图7 训练精度变化曲线Fig.7 Training accuracy curves with iterations 图8 损失函数变化曲线Fig.8 Loss function value curves with iterations 模型训练好后,用验证集的数据集对模型进行验证,记录相应的精度和损失率,同时用真实标签映射到伪标签,得出相对于真实标签数据的准确率,验证集测试结果见表4。由表4可见,用改进的K-means聚类算法训练的深度神经网络模型在伪标签的数据集上的准确率为98%,比K-means聚类的模型的98.7%低0.7%,但是在映射到真实数据上的准确率为96%,比K-means聚类的提高了4.7%。提出的模型对于加入噪声的数据具有更好的精度、损失率和真标签的准确率。 表4 验证集测试结果 综上所述,加入噪声的改进深度神经网络模型在验证集上表现的性能更好,充分说明了改进的K-means聚类算法分类的性能优于K-means算法,同时加入噪声后的聚类模型的鲁棒性更好,在进行验证集测试时,精度均大于训练集的测试精度。 在改进K-means的性能探究中,虽然提出的改进K-means算法在WC、BC和score 3个指标上均比K-means算法要稍差一些,但提出的算法与真实数据的聚类轮廓更为接近。出现上述现象的原因是:改进的算法中指定了聚类的中心阻碍了K-means随机寻找最优聚类的几率,避免在全部数据上的过拟合。实验中发现,优化初始聚类中心点、在数据中加入噪声均使WC、BC和score不佳,出现这样异常结果的原因可能是噪声数据使得数据的质量变差,同时降低了K-means算法和提出的改进K-means算法的聚类性能,但提出的算法去除了噪声点干扰和收敛性更好,因此使得训练的神经网络模型的鲁棒性得以提高。 在深度神经网络模型的性能探究中,通过观察和实验结果分析,可得出加入噪声的改进K-means聚类深度神经网络故障诊断模型表现出了优越的性能,在收敛速度和预测准确率(真实标签)表现较为突出,说明该模型具有良好的鲁棒性;也再次证明了本文提出加入噪声的改进K-means聚类算法在滚动轴承故障诊断问题上具有良好的性能。 结合分层聚类和K-means聚类的特点,提出了加入噪声的改进K-means聚类算法进行高维度的轴承振动特征数据的聚类处理。通过对比实验发现,指定K-means聚类中心、在数据中加入高斯白噪声会降低WC、BC和score聚类评价指标,但可降低了K-means聚类的随机误差,加速算法的收敛速度和防止过拟合,提高分类的准确性。同时,在聚类伪标签的基础上建立深度神经网络模型,通过半监督学习的方式进行了模型的训练和验证,实验结果显示模型的准确率高达96.2%,能够100%的区分轴承的正常状态和故障状态,具有较高的稳定性。1.3 深度神经网络模型
1.4 基于伪标签的半监督深度神经网络模型
1.5 本文的技术路线
2 实验研究
2.1 改进K-means算法的性能研究



2.2 深度神经网的性能研究

2.3 实验结果分析
3 结 论
