类氢He+在白矮星磁场范围赖曼系吸收谱的研究

刘凤丽

(黑龙江大学 物理科学与技术学院，哈尔滨 150080)

0 引 言

在量子理论建立前，人们对磁场存在下的原子光谱的兴趣已经持续了很多年，尤其是20世纪70年代在白矮星中发现强磁场(102～105T)以来，对强磁场中原子结构和光谱的研究兴趣得到了极大的增强[1-2]。对磁化白矮星中原子光谱的研究在天文应用中具有重要意义，可利用离散的光谱线来确定星体的磁场大小，从这些光谱中提取的磁场信息对于理解正常恒星向磁化白矮星的演化至关重要，并发现在确定恒星的初始质量和最终质量关系时，考虑磁场的影响是十分必要的[3-5]。另外，对强磁场中原子的结构和光谱研究也具有基本的物理意义，磁化白矮星为物理学家提供了宇宙实验室来测试描述强磁化原子的动力学理论和计算其物理性质的数值算法[1]。而白矮星的主要成分是H原子、He原子以及碱金属原子等，近几十年来，逐渐发展了对这些原子的结构和光谱的研究理论和数值算法，并取得了稳定的进展[6-14]。本课题组在这项研究工作中取得了有价值的成果[15-18]。在前期研究基础之上[19]，进一步研究白矮星磁场范围类氢离子He+的低能级之间跃迁问题，计算出给定磁场的谱线波长、振子强度和跃迁速率，并分析其随磁场变化规律。本计算结果可以作为天体物理的参考数据。

1 计算方法

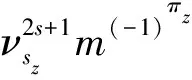
λ=κ/ΔE

(1)

ΔE=Ef-Ei

(2)

(3)

f=2(Ef-Ei)dif

(4)

(5)

2 结果与讨论

在原子核为无限质量假设前提下，首次计算在14种不同磁感应强度下类氢离子He+赖曼系8种偶极跃迁的波长、振子强度和跃迁速率，分别列于表1和表2。对于赖曼系初始状态的对称性为1 0+，其上限对应于对称性0-和(-1)+。1 0+→ν0-(ν=1-4)4种偶极跃迁的波长、振子强度和跃迁速率的计算结果见表1，1 0+→ν(-1)+(ν=1-4)4种偶极跃迁的波长、振子强度和跃迁速率的计算结果见表2，结合图1、图2和图3分别画出这8种跃迁的波长、振子强度和跃迁速率随磁感应强度γ(a.u.)变化的曲线，1 0+→ν0-(ν=1-4)4种跃迁的波长范围属于紫外线范围，见图1。由图1可见，波长随着磁感应强度γ从0.001到0.01 a.u.之间缓慢变化，但随着γ的增加而开始减小，并且γ越大减小越明显；例如γ=0.001 a.u.时1 0+→ 1 0-跃迁的吸收谱波长是303.755 62 nm，当γ增加0.01 a.u.时吸收谱波长是303.749 35 nm，波长改变量只有0.006 27 nm，但当γ=1 a.u.时吸收谱波长是273.597 07 nm，相比γ=0.001 a.u.时的波长减小30.158 55 nm；而 1 0+→ν(-1)+(ν=1-4)4种跃迁的波长范围也分布在紫外线范围，波长随着γ从0.001到0.01 a.u之间也是缓慢变化，随着γ的增加，最上面曲线即1 0+→ 1 (-1)+跃迁的波长逐渐增加，但其他3条曲线即1 0+→ν(-1)+(ν=2-4)3种跃迁的波长随着γ的增加吸收谱波长或增加或减小。例如1 0+→ 2 (-1)+的跃迁，在给定磁场γ从0.001变化到0.07 a.u.时吸收谱波长是缓慢增加的，由256.365 32 nm增至258.518 91 nm，波长改变量2.153 59 nm，当磁感应强度γ=0.1 a.u.时吸收谱波长为253.697 38 nm，较γ=0.001 a.u.时的波长减少了2.667 94 nm，当磁感应强度γ=1 a.u.时吸收谱波长为221.040 57 nm，较γ=0.001 a.u.时的波长减少了35.324 75 nm。

图1 两种偶极跃迁的波长(nm)随磁感应强度γ的变化Fig.1 Wavelengths (nm)for the two dipole transitions of He+ as a function of magnetic field strengths γ

图3 He+的两种偶极跃迁的跃迁速率随磁感应强度γ的变化Fig.3 Transition probabilities unit in a.u for the two dipoles of He+ as a function of magnetic field strengths γ

表1 He+离子1 0+ → ν 0- (ν=1-4)跃迁的波长λ (nm)、偶极强度dif和跃迁速率ωif(a.u.)随磁感应强度γ(a.u.)变化

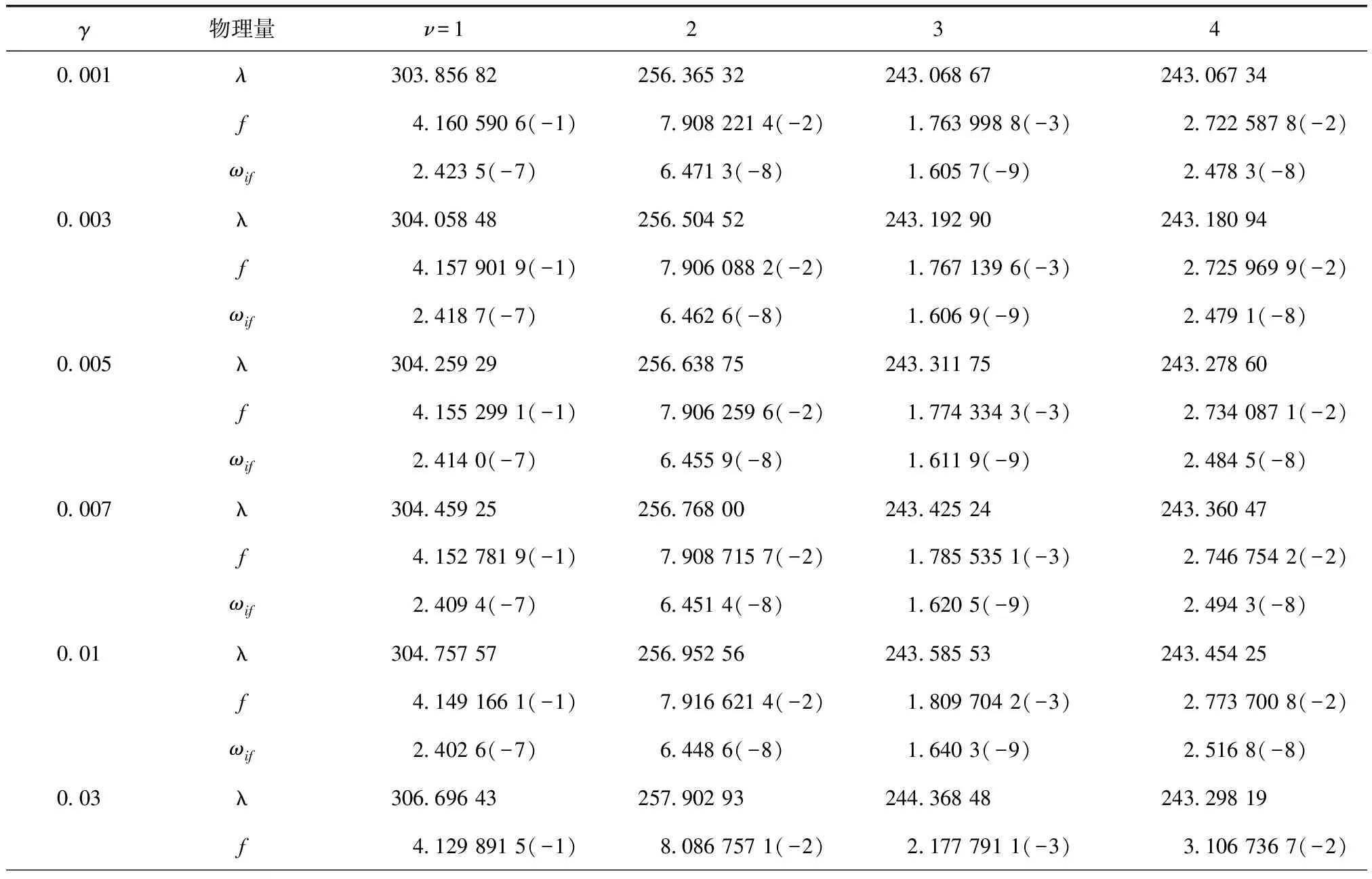
表2 He+离子1 0+ → ν (-1)+ (ν=1-4)跃迁的波长λ (nm)、偶极强度dif和跃迁速率ωif(a.u.)随磁感应强度γ(a.u.)变化

1 0+→ν0-(ν=3-4)两条跃迁谱线和1 0+→ν(-1)+(ν=3-4)两条跃迁谱线在磁场很小时分别是挨得很近的谱线，当随磁感应强度γ增加到0.02 a.u.附近两条很近的谱线开始劈裂并且随着磁场增加劈裂程度越明显，正是因为无磁场情况下，1 0+代表1s0态，ν 0-(ν=1-4)分别代表2p0、3p0、4p0和4f0态，ν (-1)+(ν=1-4)分别代表2p-1、3p-1、4p-1和4f-1态。无磁场时4p0和4f0两个能级是简并的，因此在磁场小的情况下1s0分别向4p0和4f0的跃迁的吸收谱线挨着很近，两条重合在一起的变化曲线，当磁感应强度增至0.02 a.u.时，两条重合曲线开始分离，即塞曼效应。同理，1s0分别向4p-1和4f-1跃迁的吸收谱线随磁感应强度的增加而分离也是由于塞曼效应引起的。

众所周知，观察弱跃迁的谱线是非常困难的，因此计算振子强度随磁场γ的变化具有重要的应用意义。8种跃迁的振子强度和跃迁速率随磁感应强度γ(a.u.)变化的曲线见图2和图3，由曲线规律可见，1 0+→ν0-(ν=1-4)4种跃迁和1 0+→ν(-1)+(ν=1-4)4种跃迁的振子强度变化规律分别和跃迁速率的变化规律相似，主要由于各自满足式(4)和式(5)的结果，也证明给出的数据在本理论框架上是正确的，同时在γ=0.2 a.u 时1 0+→ 4 (-1)+种跃迁的振子强度或跃迁速率很低，计算结果分别为2.253 143 2(-4)或2.247 4(-10)a.u(表2)，此时的跃迁对应的是弱跃迁，同时本文计算出谱线的强度或跃迁速率反映了在给定的磁场强度γ下，每个跃迁的初态和末态的波函数的重叠程度。

3 结 论

本文在球坐标系下采用Finite-basis-size方法计算白矮星磁场中He+的吸收光谱。目前的计算共涉及9个磁化原子态，分别是10+、ν0-(ν=1-4)和ν(-1)+(ν=1-4)，展示了与9个原子态相关的8种跃迁的波长、振子强度和跃迁速率，这些物理量作为磁场的函数，选定的磁场范围从2.35 MG到2 350 MG，这是典型的磁白矮星磁场范围。

研究得出如下结果：1)8种跃迁的波长均分布在紫外线区域；2)波长随磁感应强度的变化不具有单调性；3)He+离子1s0→ 4p0和1s0→ 4f0跃迁的谱线在无磁场时是简并的，有磁场时出现塞曼效应，谱线分离；同理1s0→ 4p-1和1s0→ 4f-1跃迁的谱线在无磁场时是简并的，有磁场时出现塞曼效应，谱线分离；4)当磁感应强度γ=0.2a.u 时1 0+→ 4 (-1)+跃迁的振子强度或跃迁速率很低，此时的跃迁对应的是弱跃迁。

本文首次计算出给定白矮星磁场范围He+的吸收光谱的波长、振子强度和跃迁速率，数据可作为天体物理的参考数据，可利用离散的光谱线来确定磁化白矮星的成分、预测星体的磁场大小，同时也可推算出其他H或类氢离子在某些特定磁感应强度下的光谱数据。从这些光谱中提取的磁场信息对理解正常恒星向磁化白矮星的演化至关重要。