基于ANSYS的简支钢板组合梁极限承载力研究
2023-12-26陈亚强
陈亚强
(青海省交通规划设计研究院有限公司 西宁 810000)
0 引言
新型钢板组合梁是由双工字钢板作为主梁,通过剪力键将钢板梁与混凝土桥面板连接形成。这种组合结构桥梁充分利用了钢材和混凝土的材料特性,具有刚度大、抗震性能好、施工建造快速方便等优点,在工程建设中得到了广泛的应用。
对于新型双肋钢板组合简支桥梁,由于其主梁间距较大,为探究横向联系、板厚等因素对桥梁极限承载能力影响程度,通过有限元对其进行精细化模拟非常有必要。目前,一些学者对钢板组合梁受力特性的研究取得了一定成果,黄玲[1]采用Midas Civil软件,对4m×30m钢板组合连续梁施工阶段受力特性进行了研究。宋超杰等[2]分析油罐车火灾下4跨钢板组合连续桥梁的极限承载能力。田建勃等[3]采用拉—压杆模型,提出小高跨比PRC连梁受剪承载力简化软化—拉压杆模型计算方法。贺耀北等[4]提出一种钢板—混凝土桥面板整体预制钢板组合梁,并采用Midas和ANSYS有限元软件对组合梁结构的力学性能进行分析。田建勃等[5]采用 ABAQUS 软件对小跨高比钢板—混凝土组合连梁内力分布进行数值分析,通过改变连梁的跨高比、钢板厚度和纵筋配筋率,详细分析了不同参数对小跨高比钢板—混凝土组合连梁混凝土应力、纵筋轴向力、钢板内力分布规律的影响。高诣民[6]通过组合梁受弯破坏足尺加载试验,研究分析预应力摩擦损失、荷载—挠度关系、跨中混凝土应变、裂缝发展以及受弯破坏特征。研究表明,我国现行预应力混凝土设计规范适用于 PC 组合梁设计。本文通过选取一跨双肋钢板组合简支桥梁(1m×35m)作为研究对象,采用ANSYS建立其有限元模型,计算了不同横梁间距、不同底板厚度及不同主梁间距下钢板组合简支桥梁的极限承载力。
1 工程背景与数值模型
选取某高速公路双肋钢板组合简支桥梁作为研究对象,单幅组合梁桥面宽度为16.75m,设计荷载等级为公路—Ⅰ级,钢主纵梁采用工字型直腹板钢梁,材料为Q345D。双主梁之间采用横梁连接,横梁之间的标准间距为7.0m,钢主梁与横梁之间采用焊接连接。混凝土桥面板与钢主梁之间通过剪力钉进行连接。
采用通用有限元软件ANSYS进行数值模型的建立,采用自底向上的建模方法。首先进行几何模型的建立,依次建立桥面板,工字钢顶板、腹板、底板,横梁以及纵向和横向加劲肋,再建立加载垫块。以共节点的方法保证模型整体性,见图1。
几何模型创建完成后,对几何模型进行单元定义,设置网格信息,生成有限元模型。其中,混凝土采用SOLID65单元,该单元除具有SOLID45单元的特性外,能够考虑混凝土的开裂和压碎。混凝土材料的本构关系采用多线性等向强化模型MISO。混凝土立方体抗压强度标准值fcu,k=50MPa,单轴抗压强度fc=22.4MPa,单轴抗拉强度ft=1.83MPa。张开裂缝的剪力传递系数βt=0.5,闭合裂缝的剪力传递系数βc=0.95。钢主梁、加劲肋及横梁等采用SHELL181单元,通过实常数来定义各个板件的厚度。将钢材与混凝土视为理想弹性材料,并且不考虑剪力钉的滑移效应,因此以共节点的方式来模拟实体单元与板单元之间的连接。按照简支梁的实际支座布置情况对有限元模型施加边界条件,有限元模型共有7870个节点,共有5038个单元,见图2。
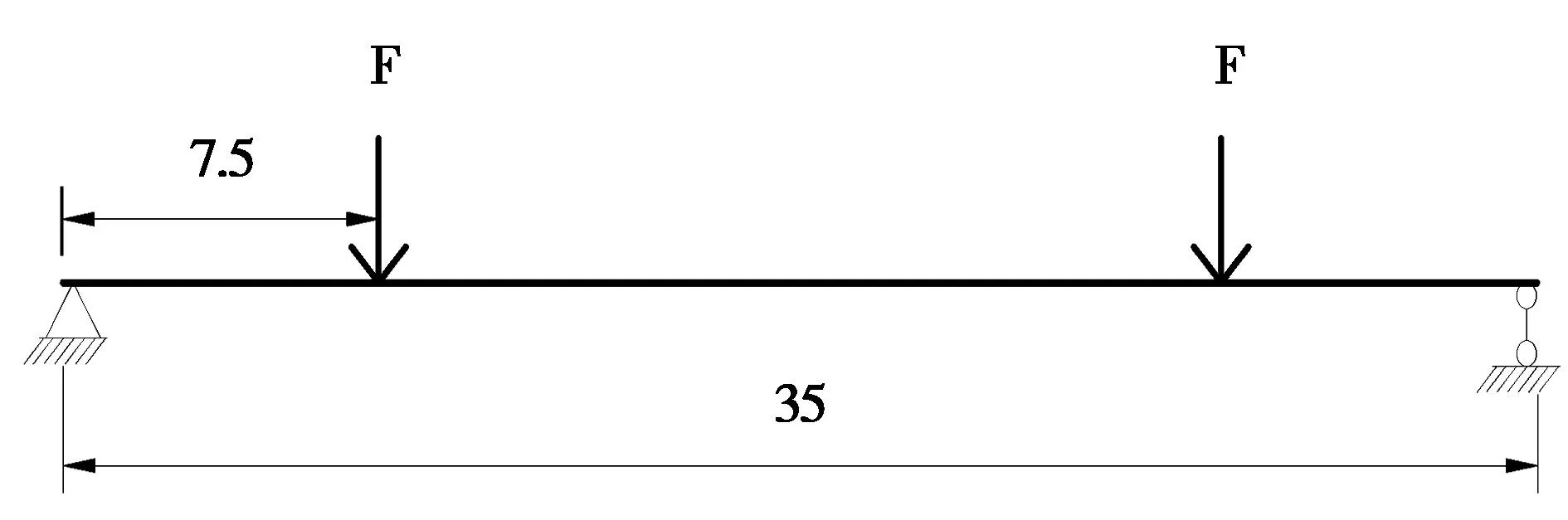
有限元模型建立完成后,进行荷载的添加,实际荷载多为面荷载,因此模型中若采用点荷载,容易引起加载点处混凝土过早开裂或压碎,造成计算时收敛困难。支座支撑处同样会引起应力集中,不易收敛。为此,建立加载垫块施加面荷载,在支撑处增大单元尺寸。加载时采用四分点加载的方式,构造纯弯段,见图3~4。
2 不同横梁间距下简支钢板组合梁极限承载力分析
将简支钢板组合梁横梁间距取为3m、4m、5m、6m,来研究不同横梁间距下简支钢板组合梁的极限承载力。在有限元模型的垫块上施加面荷载,可得到不同荷载作用下简支钢板组合梁跨中下缘位置处的荷载位移曲线。图5~8为不同横梁间距下跨中下缘位置处的荷载位移曲线。
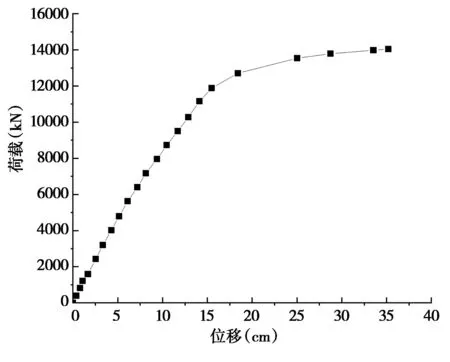
图5 横梁间距3m跨中下缘处荷载位移
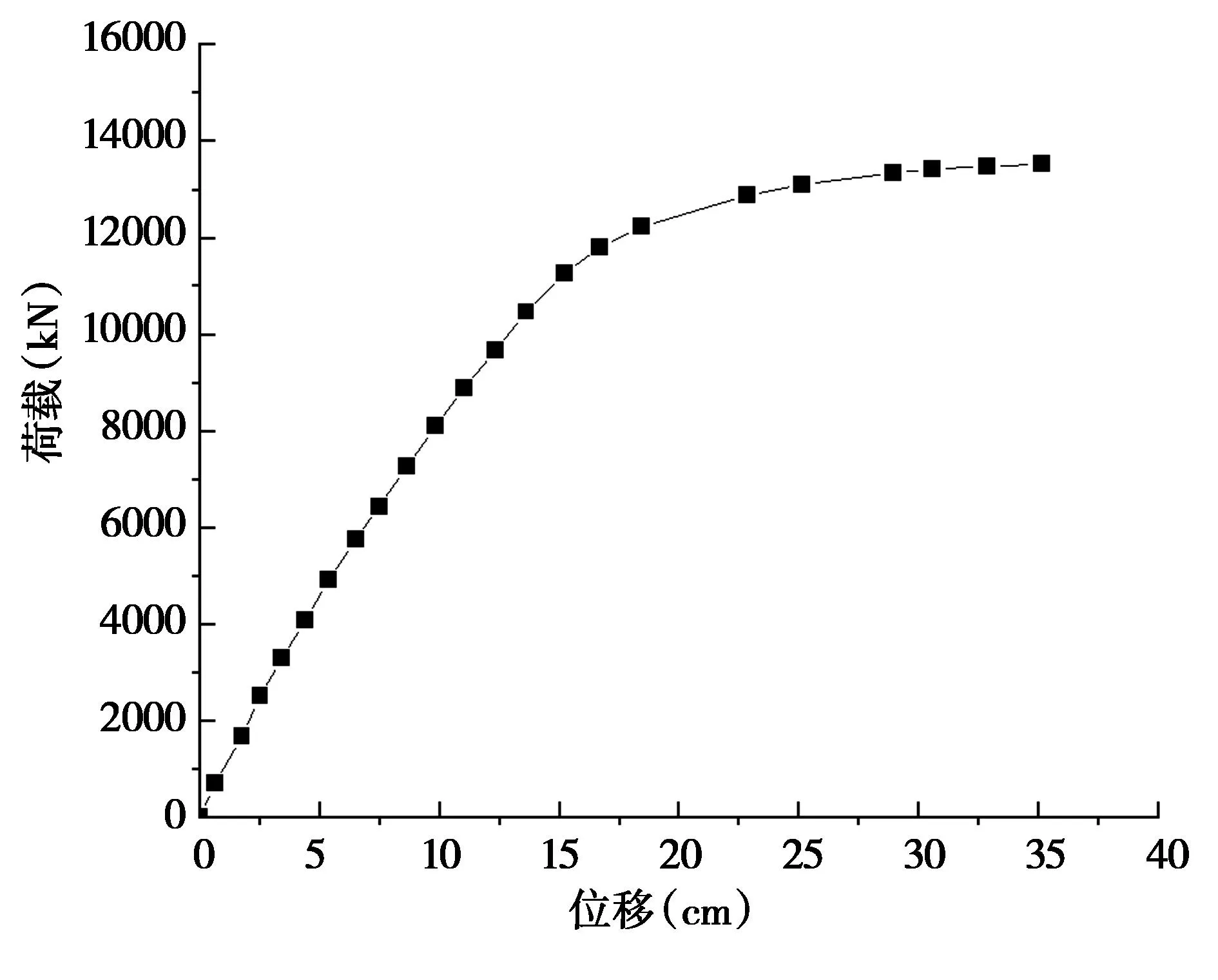
由图5~8可知,支点横梁间距为3m时,极限承载力F为14200kN,对应跨中下缘最大挠度为41.6cm;支点横梁间距为4m时,极限承载力F为13700kN,对应跨中下缘最大挠度为40.5cm;支点横梁间距为5m时,极限承载力F为13600kN,对应跨中下缘最大挠度为52.6cm;支点横梁间距为6m时,极限承载力F为12500kN,对应跨中下缘最大挠度为39cm。
由上可知,随着横梁间距的增大,简支钢板组合梁的极限承载力也不断降低。将横梁间距3m、4m、6m时的极限承载力与原设计(5m)分别作对比得到其承载力分别增加4.4%、增加0.7%、降低8.1%。
对比于原设计横梁间距5m,减小横梁间距并不能将承载能力提高很多。且会增加材料的用量以及施工时的难度。增大横梁间距到6m时,承载能力下降8.1%,且破坏时横梁处应力先达到屈服,不符合经济安全的要求。综上可得,将横梁间距取为5m对于此种桥型来说更为理想。
3 不同底板厚度下简支钢板组合梁极限承载力分析
将简支钢板组合梁底板厚度取为4.0cm、4.5cm、5.0cm(原设计)、5.5cm、6.0cm,来研究不同底板厚度下简支钢板组合梁的极限承载力。在有限元模型的垫块上施加面荷载,可得到不同荷载作用下简支钢板组合梁跨中下缘位置处的荷载位移曲线。图9~12为不同底板厚度下跨中下缘位置处的荷载位移曲线。
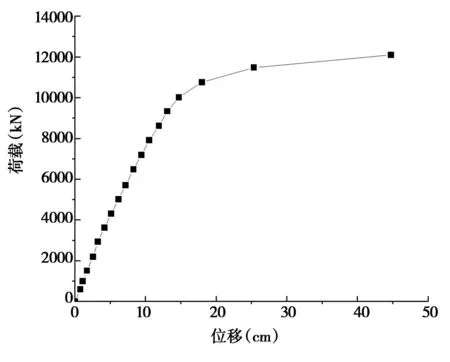
图9 底板厚度4cm跨中下缘处荷载位移
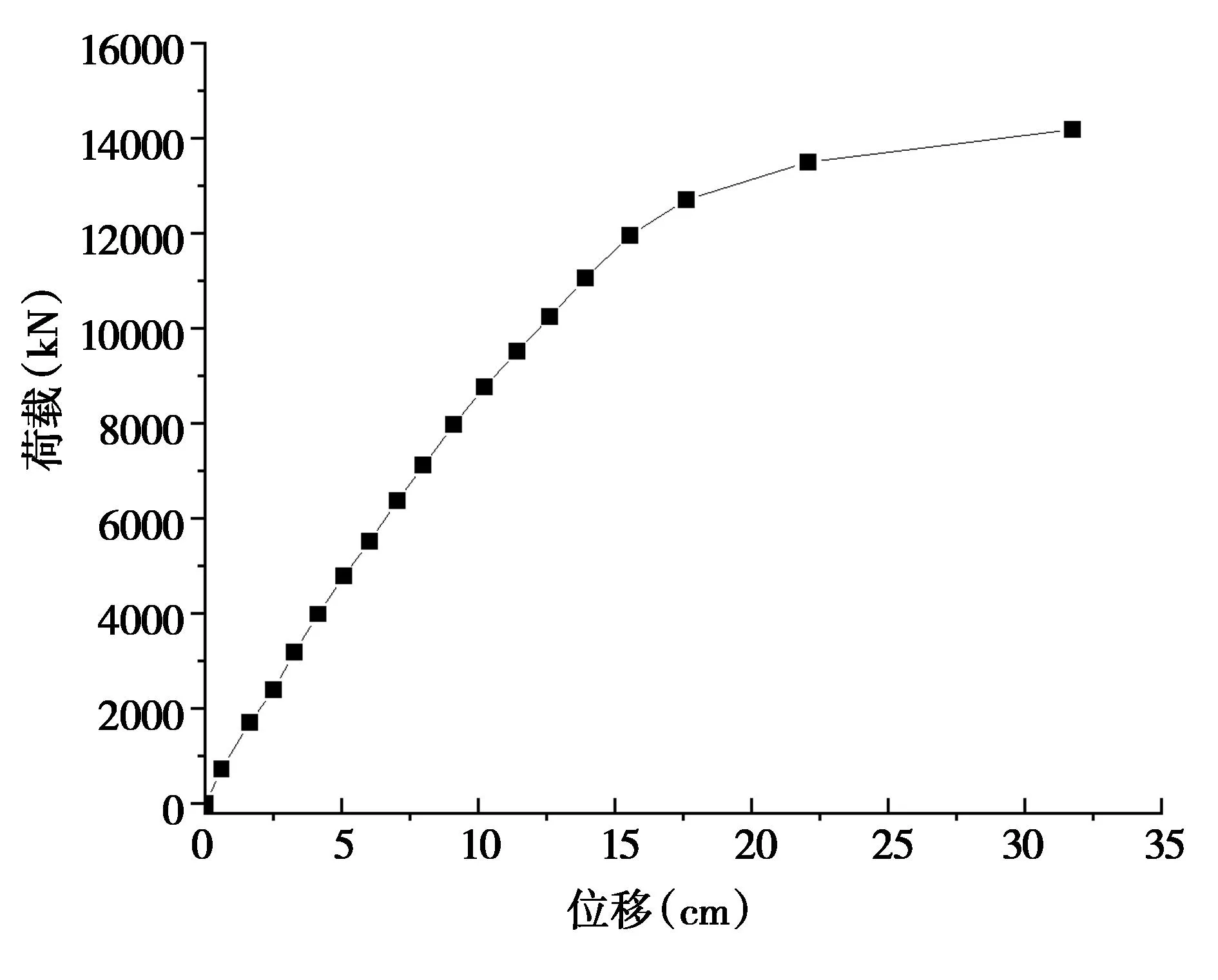
由图9~12可知,底板厚度为4cm时,极限承载力F为12100kN,对应跨中下缘最大挠度为44.8cm,对应跨中下缘最大正应力为388MPa;底板厚度为4.5cm时,极限承载力F为12900kN,对应跨中下缘最大挠度为43.1cm,对应跨中下缘最大正应力为391MPa;底板厚度为5.5cm时,极限承载力F为14200kN,对应跨中下缘最大挠度为47.8cm,对应跨中下缘最大正应力为392MPa;底板厚度为6.0cm时,极限承载力F为14250kN,对应跨中下缘最大挠度为41.3cm,对应跨中下缘最大正应力为392MPa。
将不同底板厚度时的极限承载能力进行对比,如图13所示;将不同底板厚度下对应的跨中下缘挠度进行对比,如图14所示。
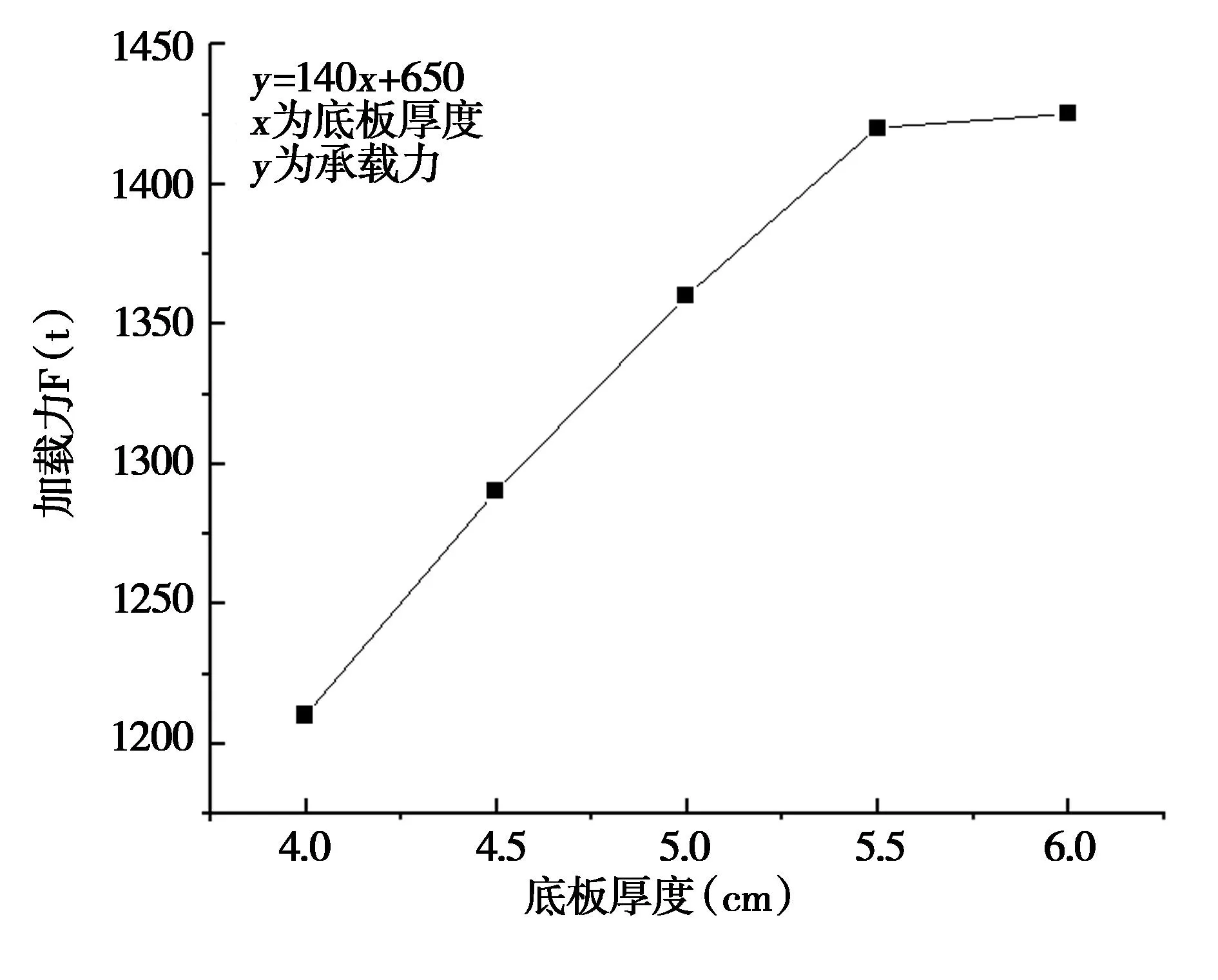
由图13可知,随着底板厚度的增加,简支钢板组合梁的极限承载力也在近似线性的提高,以底板厚度为x,单位取cm,以承载力F为y,可建立线性方程y=140x+650来模拟两者的关系。但当底板厚度>5.5cm之后,因破坏形式的改变,此式不再适用。
由图14可知,随着底板厚度的增加,达到极限承载力时跨中下缘挠度逐渐减小。以底板厚度为x,单位取cm,以跨中下缘挠度为y,单位取cm,可建立线性方程y=-11x+88.8来模拟两者的关系。
4 不同主梁间距下简支钢板组合梁极限承载力分析
将简支钢板组合梁主梁间距取为10.0m、10.2m、10.4m、10.6m,来研究不同主梁间距下简支钢板组合梁的极限承载力。在有限元模型的垫块上施加面荷载,可得到不同荷载作用下简支钢板组合梁跨中下缘位置处的荷载位移曲线。图15~18为不同主梁间距下跨中下缘位置处的荷载位移曲线。

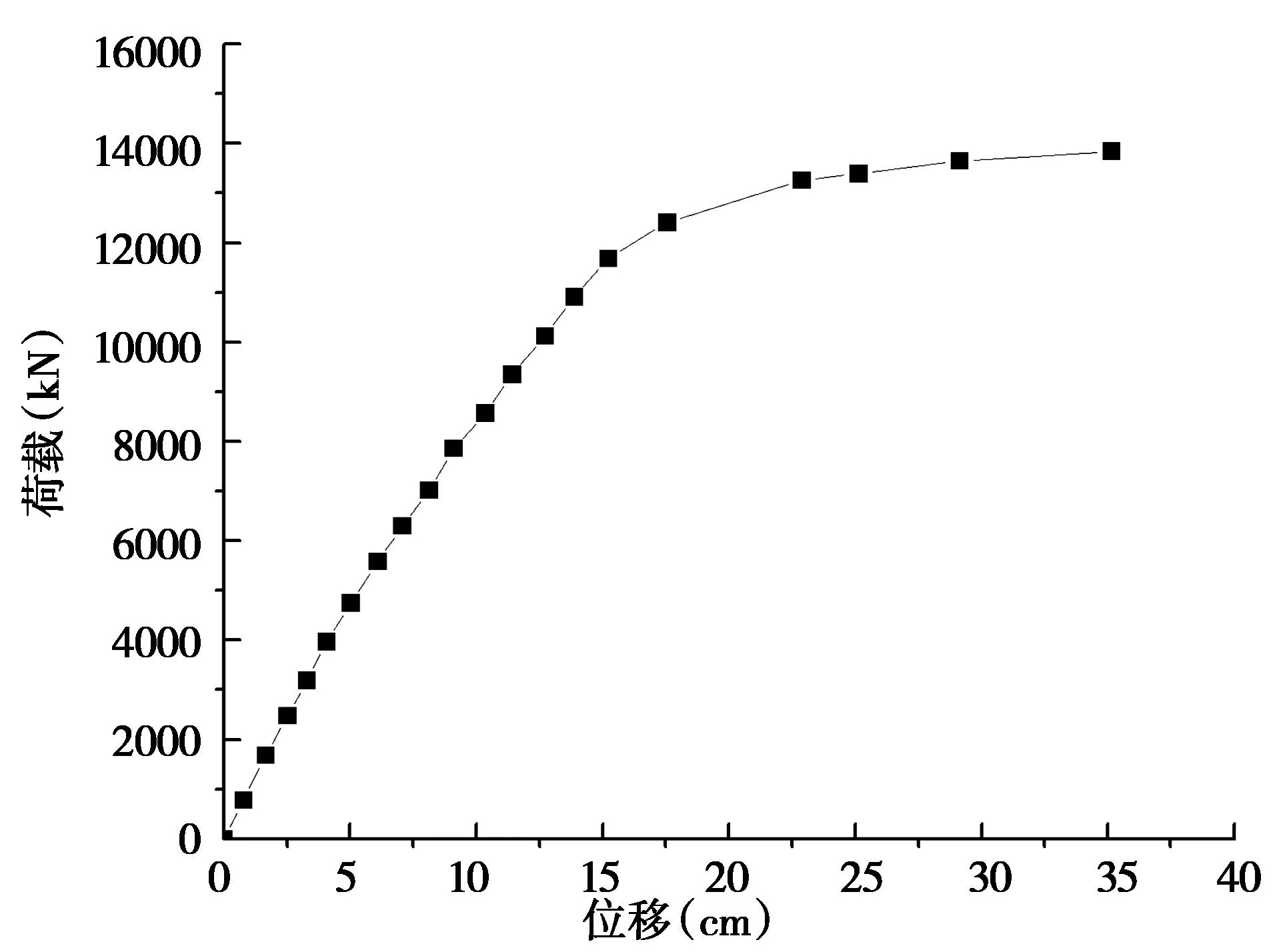
由图15~18可知,主梁间距为10.0m时,极限承载力F为14150kN,对应跨中下缘最大挠度为40.9cm,对应跨中下缘最大正应力为391MPa;主梁间距为10.2m时,极限承载力F为14000kN,对应跨中下缘最大挠度为45.3cm,对应跨中下缘最大正应力为389MPa;主梁间距为10.4m时,极限承载力F为13800kN,对应跨中下缘最大挠度为45.3cm,对应跨中下缘最大正应力为391MPa;主梁间距为10.0m时,极限承载力F为13600kN,对应跨中下缘最大挠度为54.2cm,对应跨中下缘最大正应力为393MPa。
将不同主梁间距下的极限承载能力进行对比,如图19所示;将不同主梁间距下对应的跨中下缘挠度进行对比,如图20所示。
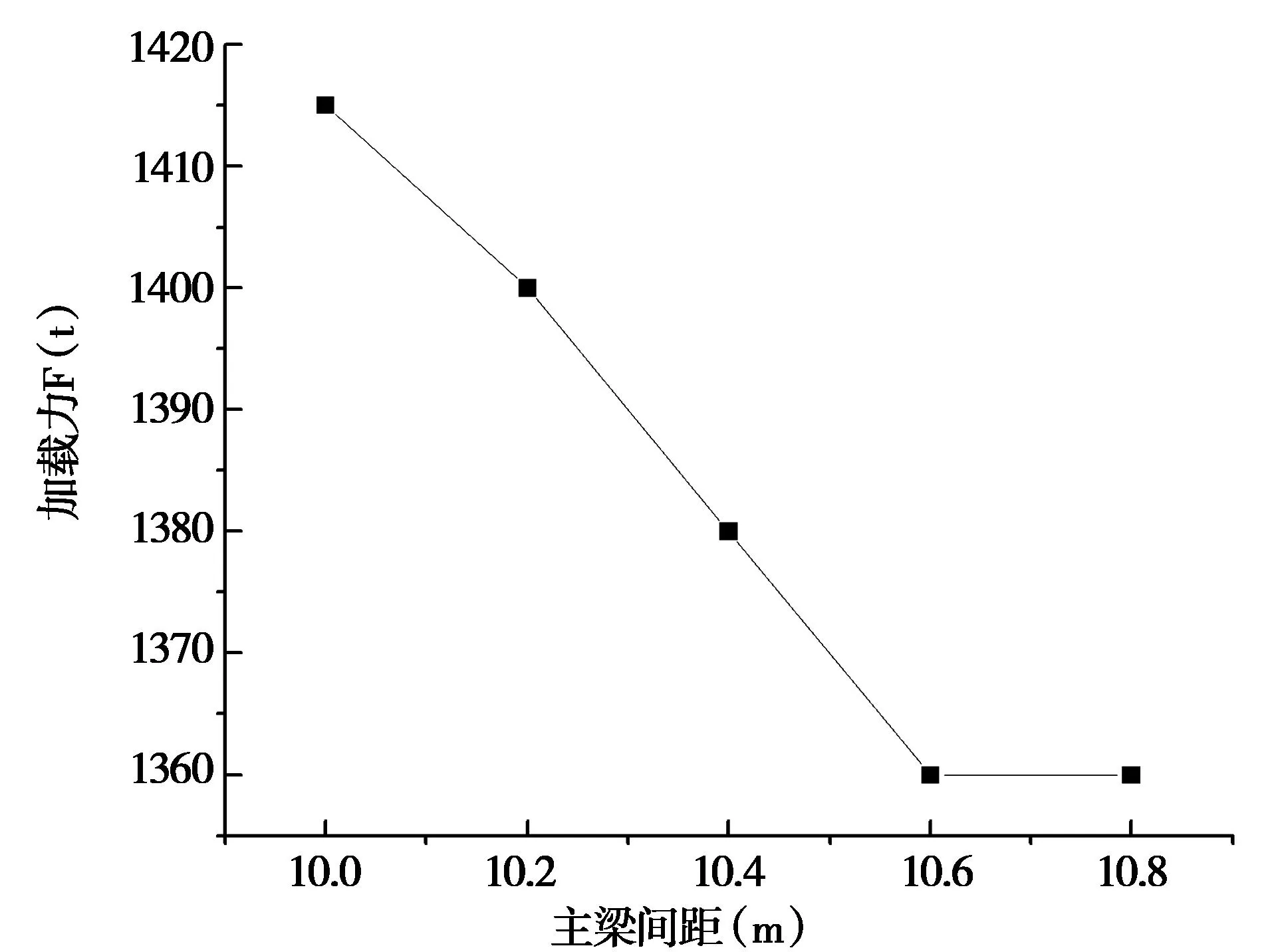
由图19可知,当主梁间距在10.0m到10.6m之间时,主梁间距与极限加载力F近似呈单调递减线性关系。以主梁间距为x,单位为m,以最终承载力F为y,单位为t,可近似用线形方程y=-91.67x+2331.7来模拟。当主梁间距处于10.6到10.8m之间时,承载能力基本不变。
由图20可知,随着主梁间距的增大,跨中下缘挠度总体趋势是增加的。最大为10.6m时,为54.2cm,最小为10.0m时,为40.9cm,两者相差13.3cm。
5 主梁最大承载力分析计算
根据上述横梁间距、底板厚度以及主梁间距对于梁极限承载力的影响,取横梁间距5.0m,底板厚度5.5cm,主梁间距10.0m,进行极限承载力计算。加载方式与边界条件均与上述相同,可得到跨中下缘荷载位移曲线,如图21所示,提取其纵向正应力图,如图22所示。
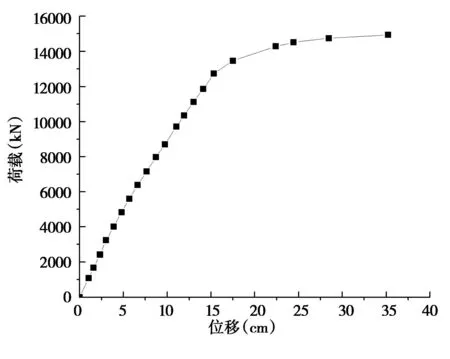
图21 跨中下缘荷载位移曲线
由图21可知,当力F达到14900kN时,不再收敛,即最大承载力F为14900kN。此时跨中下缘最大位移为35.1cm,跨中下缘纵向正应力为348MPa。由图22可知,整个结构最大位移为40.1cm,最大正应力为389MPa。
对比原结构最大承载力13600kN,跨中下缘最大位移35.2cm,在板厚度加大到5.5cm,主梁间距缩小到10.0m的工况下,跨中下缘最大位移基本不变,承载力可提高9.6%。
6 结论
根据以上研究,得出以下结论:
(1)底板厚度以及主梁间距不变时,将横梁间距减小,可得到较大的承载能力。从经济、施工方便、结构稳定等方面综合考虑,建议取横梁间距为5.0m为宜。
(2)横梁间距以及主梁间距不变时,在一定范围内增加底板厚度,可获得较大的承载能力。底板厚度在4.0~5.5cm范围时,承载力可由线性方程y=140x+650来计算。跨中下缘挠度可由线性方程y=-11x+88.8来计算。综合考虑,取底板厚度为5.5cm时可获得较大承载力。
(3)横梁间距以及底板厚度不变时,在一定范围内缩小主梁间距时,可获得较大承载力。主梁间距小于10.0m,则悬臂过大,不进行分析。主梁间距在10.0m至10.6m范围时,承载力可由线性方程y=-91.67x+2331.7来计算。10.6m至10.85m范围内承载力基本不变。主梁间距在10.0m至10.85m范围内,随着间距增大,跨中下缘挠度总体呈增加趋势,最大差值可达13.3cm。
(4)取横梁间距5.0m,底板厚度5.5cm,主梁间距10.0m,可获得此三种参数变化下的最大承载力。跨中下缘挠度与原设计基本一致,承载力可提高9.6%。
