欧式木窗双端铣床自动化生产翻折机构优化设计研究

吴 哲 孙学军 任长清 张中弛 丁禹程

（东北林业大学机电工程学院，黑龙江 哈尔滨 150040）

木材加工业是一个绿色低碳产业，具有储碳减排的特点，同时其产品可再生可降解性强，符合当下国家经济发展的要求，在“双碳”背景下具有广阔的前景[1-4]。

木窗双端铣机床是加工欧式木窗的重要设备，可将木窗四边框铣削成需要的形状。传统双端铣机床铣削过程需要人工配合完成此工作。为了提高生产效率，设计出了一套其专用的自动化生产线。在双端铣机床实际使用过程中，需要定期开门对其进行维护，而生产线结构及安装位置限制了开门这一过程。为解决这一问题，在机床开门处设计了可以抬升的辊台，该装置利用气缸提供动力，推动滑块作直线运动，而后通过连杆将力传递到上辊台实现辊台翻折。因此，在翻折过程中，装置的运动性能对装置的稳定及寿命有较大影响。鉴于此，有必要对双端铣床翻折机构的运动进行分析，并针对其具体问题进行优化。

研究者对装置运动过程进行了运动仿真分析，验证了模型运动过程与理论的一致性[5-7]，并在铰接点位置对机构性能开展了广泛研究[8-11]。例如，通过Adams对机构进行动力学分析，并对机构压力角进行优化[12-14]。葛正浩等[15]基于Adams对烟包裹包凸轮连杆机构进行了动力学分析，并提出了机构的改进方案。曹俊宏等[16]以最小驱动转矩为优化目标，基于机构运动学与动力学特性，分析建立了倒伏机构的模型，并通过数值计算优化其结构参数，最后利用Adams对优化结果进行了验证。苑伍德等[17]在Adams中建立了某T式举升机构的虚拟样机模型，对其进行仿真分析并采用 OPTDES 广义梯度算法，以举升机构液压油缸作用力最小为优化目标，对该机构进行了优化。叶柳等[18]利用多目标优化的方法构造多目标函数，以机构的最大高度、急回特性和最大加速度为优化目标，对机构进行了优化。还有研究者通过Pro/E软件对机构进行运动仿真，借助仿真结果对运动构件的运动规律进行了分析[19-21]。此外，还可以通过建立装置参数化模型求得工作性能最优解的方法对装置进行优化[22-30]。

本文拟通过Solidworks建立翻折三维模型，并对辊台及连杆进行受力分析，根据分析结果选用合适的气缸。在Solidworks中对装置进行简化，导入Adams进行运动学分析，并对得到的结果进行分析。随后，通过添加缓冲部件的方法对装置受到的冲击进行优化，以期降低装置执行运动末端受到的冲击，从而提升装置的可靠性和使用寿命。

1 装置总体结构介绍

图1为装置的安装示意图。从图中可知，该装置的辊台由上下两部分组成，上下辊台安装有绕定轴自转的辊子，工作时木窗由辊子转动带动向前做进给运动。同时，上下辊台也对木窗具有夹持作用，从而保证了铣削过程的稳定。上辊台安装翻折机构，其结构如图2和图3所示，主要由气缸、辊台、支撑杆、滑块组成。在铣床正常工作时，气缸处于收缩状态，辊台保持水平。在机床需要维护时，气缸伸出，推动滑块沿导轨向前移动，滑块带动支撑杆将辊台向上翻折，到达极限位置时辊台抬起。此时，工作人员可进入并打开机床门进行换刀作业。为了保证机床门可以顺利完全开启，翻折机构设计为单边支撑。

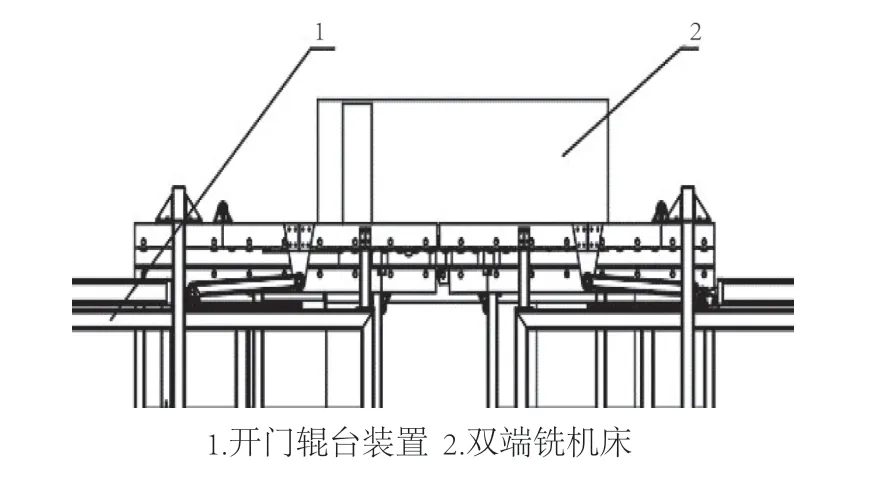
图1 开门辊台安装示意图Fig.1 Installation diagram of door opening roller table

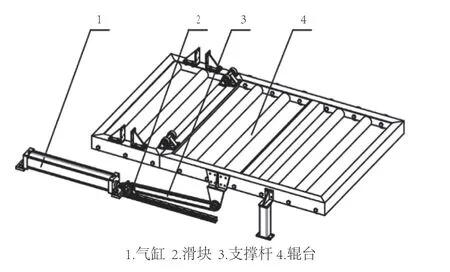
图2 翻折机构工作状态示意图Fig.2 Working state diagram of folding mechanism

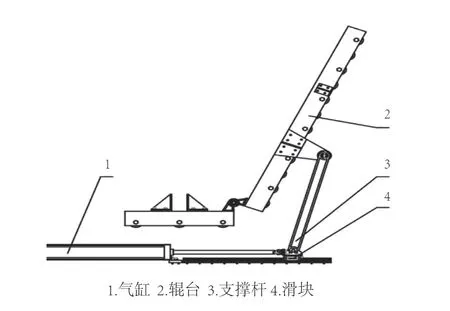
图3 翻折机构换刀状态示意图Fig.3 Folding mechanism tool change state diagram

2 气缸选型

2.1 计算前的准备

在翻折机构中，气缸最主要的作用是提供动力，通过支撑杆将上辊台翻折至开启状态。在此过程中，需要克服辊台自身的重力。为方便分析，利用Solidworks软件建立了辊台模型，并定义材料，利用软件质量属性功能，得到上辊台质量为232.98 kg。为便于后续的计算过程，在图中生成质心特征，并将其标注在二维图中，如图4 所示。

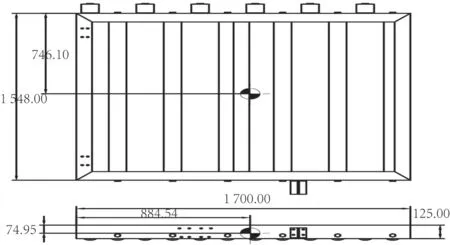
图4 质心位置Fig.4 Centroid position

根据实际尺寸按1 ∶1 绘制机构运动简图，如图5所示。

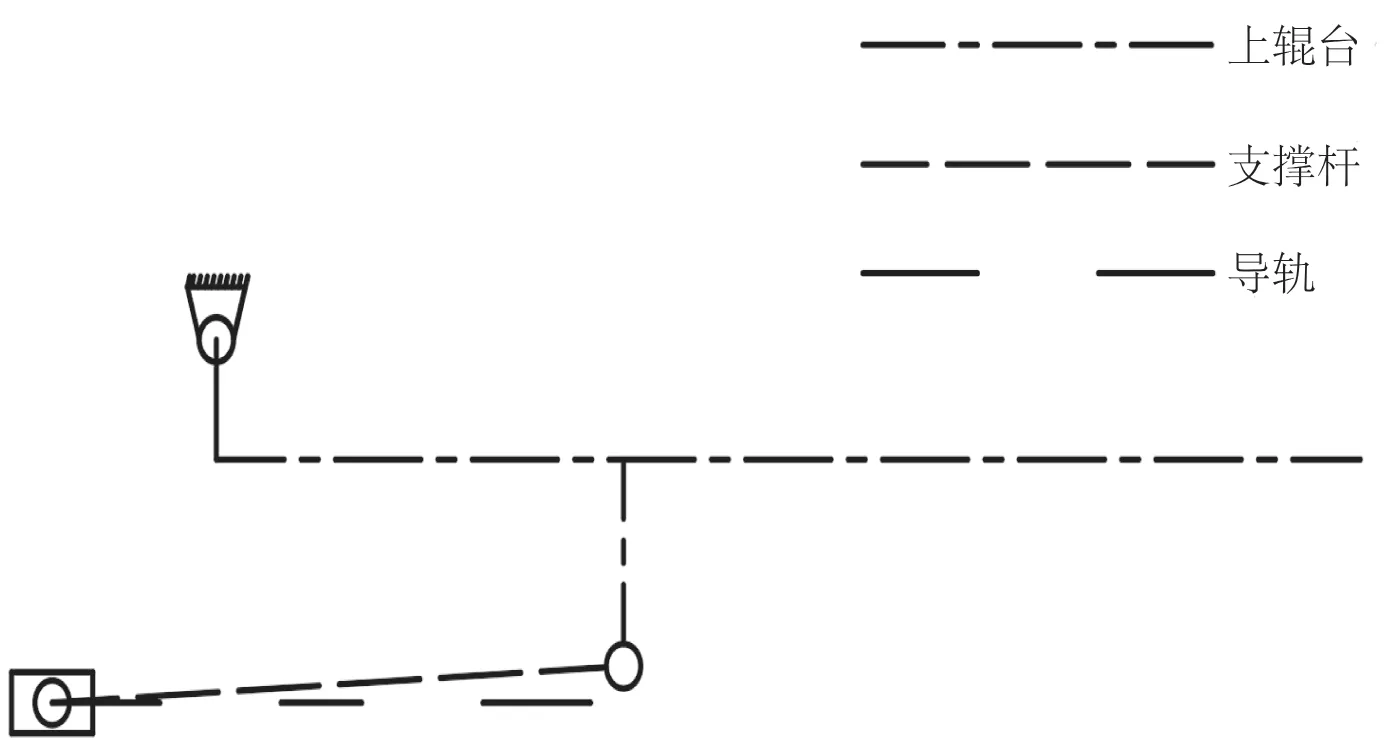
图5 机构运动简图Fig.5 Mechanism motion diagram

2.2 分析计算

翻折机构是由用来传递运动和力的结构件组成的系统，故应具有确定的运动。机构具有确定运动的条件是：机构自由度必须大于零，且机构自由度的数目等于原动件的数目。因此，首先需要对机构的自由度进行计算。机构运动简图如图5所示。由图可知，翻折机构中原动件为滑块，原动件数目为1。根据公式（1）计算得出自由度：

式中：n为活动构件数目；Pl为低副数目；Ph为高副数目。

由机构运动简图可知，活动件数目n=3，分别为滑块、支撑杆与辊台。低副数目Pl=4，分别为3个转动副和1个移动副。高副数目Ph=0。带入自由度公式得F=1，故机构具有确定运动。

滑块作为翻折机构的原动件，动力来自于气缸，因而气缸推力的大小直接决定机构能否正常运行。因此，需要对气缸推力进行计算。

为计算支撑杆的支撑力，首先隔离上辊台，并对其进行受力分析，如图6所示。图中重力G所在位置根据图4质心位置标出。根据公式（2）计算得出支撑杆的支撑力，其数值为F=5 095.63 N。

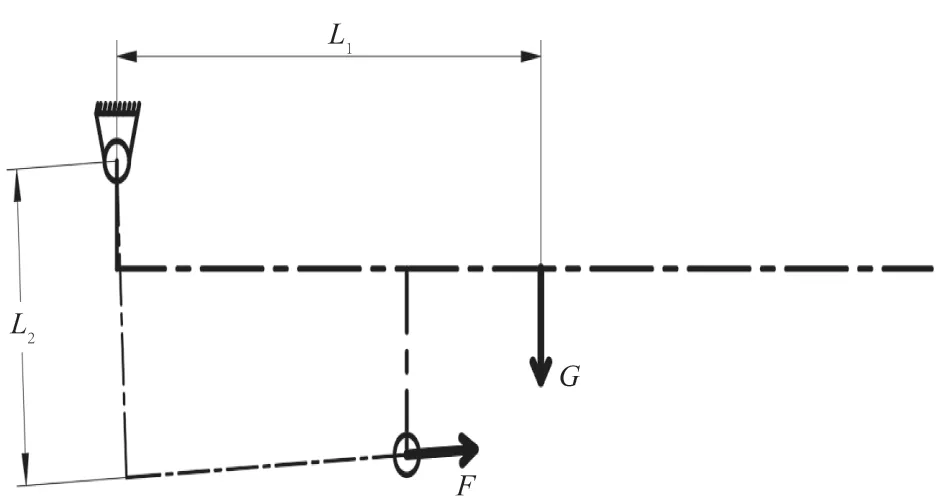
图6 上辊台受力分析图Fig.6 Upper roller table force analysis diagram

式中：F为支撑杆支持力，N；G为上辊台重力，N；L1为G对应的力臂，mm；L2为F对应的力臂，mm。

为计算气缸的推力，隔离支撑杆进行受力分析，如图7所示。根据公式（3）计算得出气缸推力，其数值为F缸=5 089.42 N。

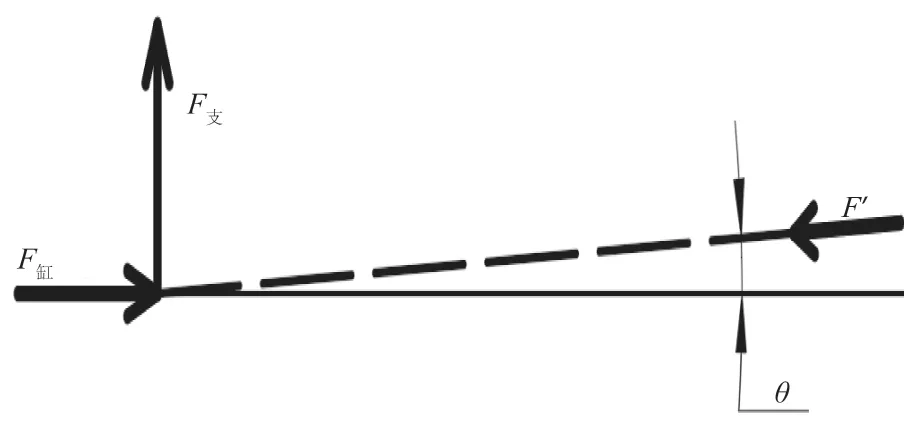
图7 支撑杆受力分析图Fig.7 Stress analysis diagram of support rod

式中：F'为辊台对支撑杆的作用力，N；θ为初始位置夹角，°；F缸缸为气缸推力，N。

根据上述计算结果及实际安装使用情况，考虑到摩擦及其它阻力的影响，选取气缸型号为SC125×800，理论推力为6 140 N。

3 动力学分析

为探究翻折机构在运动过程中的稳定性，对翻折机构进行运动学分析。

3.1 仿真过程

为简化软件的运算，首先将原有的完整建模实体简化为仅保留关键运动部件，以及对仿真结果有较大影响的部件。然后，将简化后的模型导入Adams中，简化后的模型如图8所示。

图8 简化后的模型Fig.8 Simplified model

为装置各部件定义质量属性，限制滑块在导轨的行程为原有气缸的行程0～800 mm，在原有安装气缸的部位添加气缸的推力F推=6 140 N，最后为装置添加重力环境g=9 806 mm/s2。然后，对辊台质心与滑块质心处位移速度及加速度进行计算，生成辊台质心与滑块质心位移、速度与加速度曲线分别如图9和图10所示。

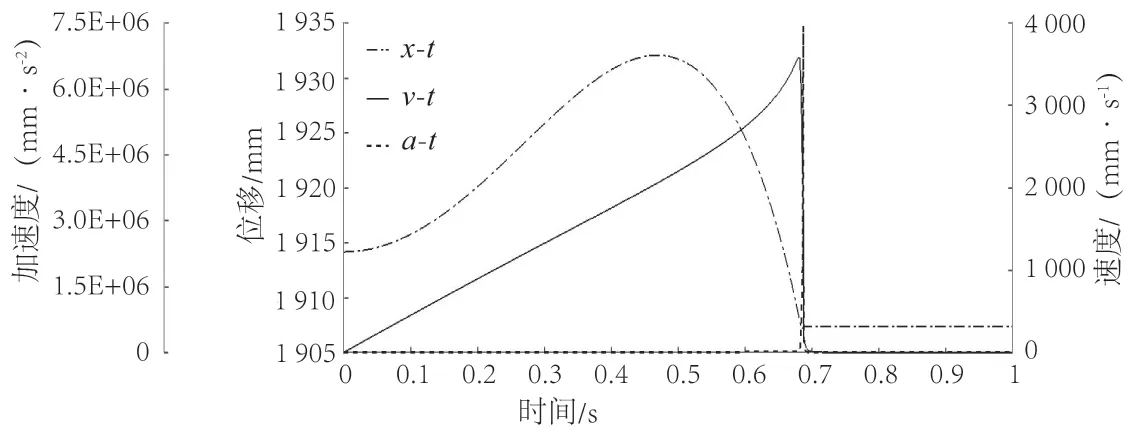
图9 辊台质心位移、速度和加速度曲线Fig.9 Curves of displacement, velocity, and acceleration of roller center of mass

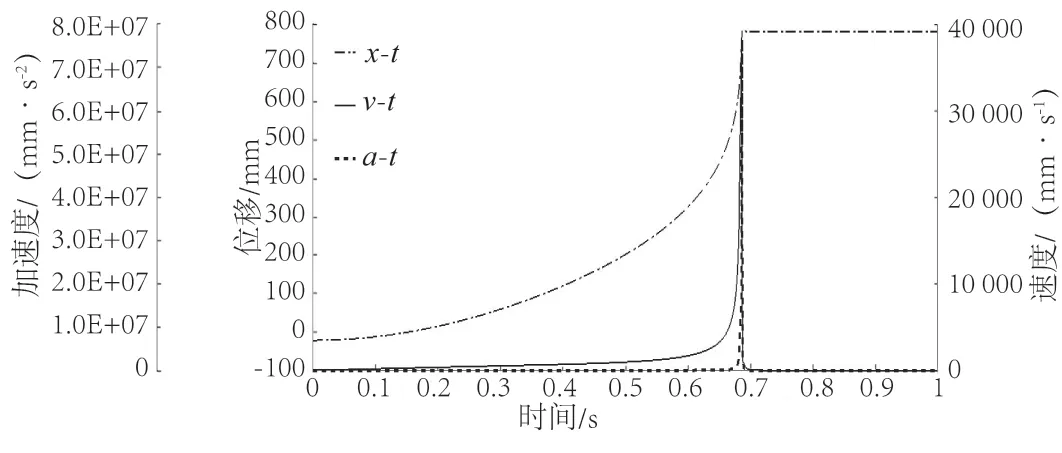
图10 滑块质心位移、速度和加速度曲线Fig.10 Curves of displacement, velocity, and acceleration of slider centroid

3.2 图像分析

由图9可知，辊台在运行过程中速度在不断增大，其斜率在前期几乎不变。大约在0.68 s后，气缸到达最大行程，随即速度和加速度突变为零，位移保持不变。可见，其在运行过程中的前期处于类似匀加速的直线运动状态，在大约0.68 s时，线速度达到最大值（3 551.07 mm/s），而后突然停止。如图10所示，滑块的加速度和速度与辊台图中观测到的情况类似，同时在行程末端，其速度和加速度也达到最大值，随即突变为0。综上可知，在气缸的行程末端，翻折机构的上辊台与滑块受到了强烈冲击。

3.3 影响辊台冲击的因素

在翻折机构中，翻折辊台质量占比最大，其宽度约1.5 m，长度约1.7 m。若受到过大的冲击，随着使用次数的增多，最终可能导致机构提前破坏。因此，其受到的冲击应在合理的范围内，并尽量减小冲击带来的负面影响。

由图9和图10可以看出，辊台速度与滑块速度存在明显的对应关系。为进一步分析，假设滑块运动到了任意位置C点，如图11所示，同时为了便于计算，将辊台两铰接点连接起来简化为AB杆。

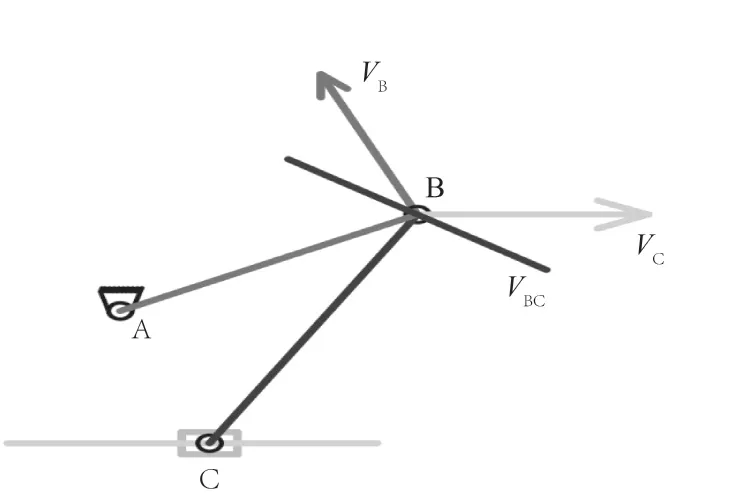
图11 中间状态速度分析Fig.11 Intermediate state velocity analysis

当滑块运动到此位置时，支撑杆上两端分别连接滑块与辊台，因此滑块速度VC大小方向均已知，在图中以箭头VC表示。AB杆绕定轴做旋转运动，因而VB方向为垂直AB杆向上，在图中以箭头VB表示。点B相对点C的速度VBC，方向垂直BC杆，但具体朝向未知，在图中以直线VBC表示。此时，同一构件上的两点速度存在以下关系：

图12 中间状态速度三角形Fig.12 Middle state velocity triangle

4 优化设计

4.1 优化方案设计

通过上述分析得知，上辊台在运动末端受到了冲击，且此冲击影响较大，故应当在满足机构使用前提下将冲击尽量减小。根据上述分析可知，辊台速度与滑块速度存在关系：

可见，辊台速度与滑块线速度成正比。因此，针对辊台速度的优化便可转变为对滑块速度的优化。经此优化，辊台与滑块的冲击都可得到改善。

根据对本机构的分析可知，后期加速度的过度上升，主要原因是随着滑块的向前运动，气缸运行过程中受到的辊台间接施加的阻力逐渐减小，从而使得滑块在运动方向所受的合外力逐渐增大。因此，需要添加一个能随位移变化的力来延缓这种情况。在机械结构中，由于弹簧有着随压缩距离增大弹簧力逐渐增大的特性，非常适合本机构使用。此外，弹簧的成本较低。因此，只需要选择合适的弹簧K值，便可以满足该机构缓冲要求。

如图13所示，在优化方案中，在滑块运动运动路径上添加了一个压缩弹簧，在运动后期，通过气缸推动滑块压缩弹簧来使弹簧对滑块施加一个反作用力，从而使得对气缸的推力得到有效缓冲。

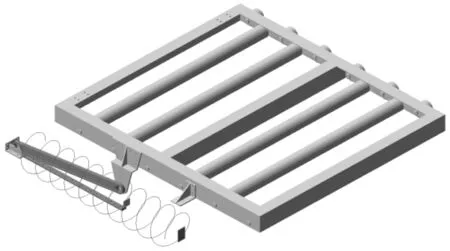
图13 Adams中弹簧位置示意图Fig.13 Spring position diagram in Adams

4.2 弹簧K值的确定

在复杂的机构设计中，需要分析的情况也非常复杂。若全部采用人力计算，那么效率会大大降低。同时，由于计算的复杂性，往往会由于考虑不全面或在大量的计算中出现误差而导致计算错误。为提高设计效率，本文提出了一种新的求解思路，即利用二分法思想，结合Adams仿真软件，确定弹簧的K值。二分法寻优流程如图14所示。

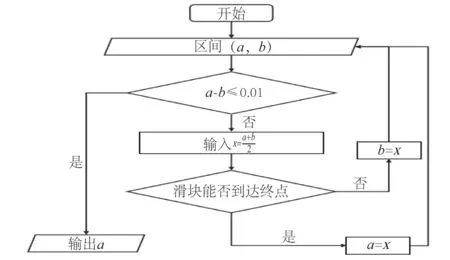
图14 二分法寻优流程图Fig.14 Dichotomy optimization flow chart

在执行寻优流程前，首先需要确定K值的大致范围。为了使滑块能够运动到指定位置停止，且恰好不反弹，在不考虑摩擦及其它阻力的影响下，弹簧最大压缩量为800 mm，则弹簧力为：

通过计算可得K=7.675。考虑到实际过程中摩擦力的存在，且K值过大可能会导致滑块无法到达末端，粗估K值最优值区间为7.0～8.0 N/mm。为进一步验证，在Adams模型中将弹簧K值分别设定为7.0 N/mm和8.0 N/mm，通过仿真分析得知，当K=7.0 N/mm时，滑块顺利到达指定位置；而当K=8.0 N/mm时，滑块在达指定位置前发生反弹，且无法到达终点。因此，可以确定K的最优值就在此区间内。为提高设计效率，采用二分法寻优方法确定具体的K值。

首先，在此流程中将初估的K值区间（7.0～8.0 N/mm）输入，判断a-b≤0.01的意义在于控制输出结果距离实际最优值的精度，若精度要求高，那么可以将0.01再次下调。随后开始仿真，发现经过7次仿真，便可输出结果为7.703 N/mm，同时最优解有逼近7.7 N/mm的趋势。因此，将K=7.7 N/mm再次带入仿真，发现其能够满足使用条件，因此，将弹簧的K值设定为7.7 N/mm。

将优化后得到的辊台、滑块速度、加速度曲线分别与优化前的速度、加速度进行对比，如图15～18所示。

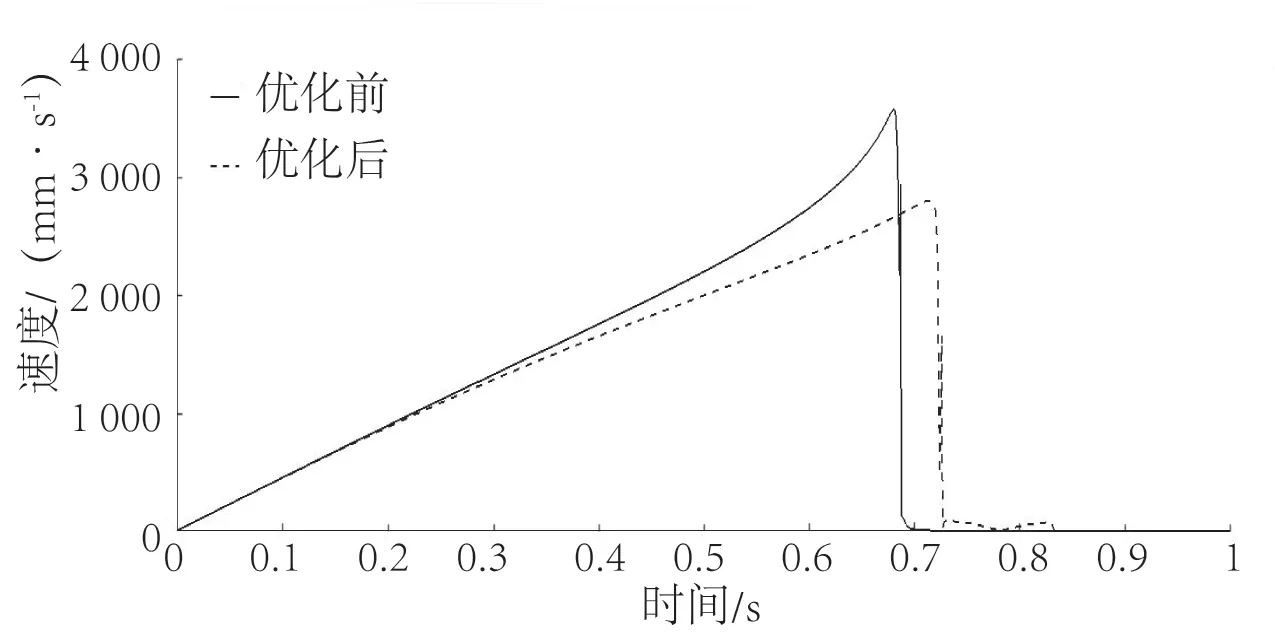
图15 辊台速度优化前后对比Fig.15 Comparison of roller speed before and after optimization

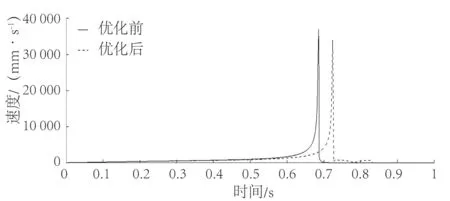
图16 滑块速度优化前后对比Fig.16 Comparison of slider speed before and after optimization

图17 辊台加速度优化前后对比Fig.17 Comparison of roller table acceleration before and after optimization

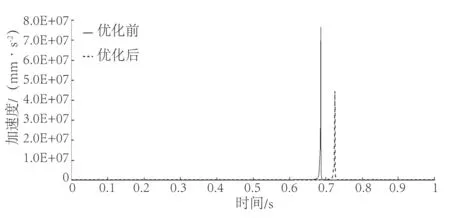
图18 滑块加速度优化前后对比Fig.18 Comparison of slider acceleration before and after optimization

4.3 优化结果分析

由图可知，在添加弹簧后，机构依然可以顺利完成所需运动，且在优化后的辊台速度和加速度峰值明显低于优化前。软件测试结果显示，优化前辊台峰值速度为3 551.07 mm/s，优化后峰值速度为2 801.29 mm/s，减小了21.1%。同时，优化前辊台峰值加速度为7.42×106mm/s2，优化后峰值加速度为4.49×106mm/s2，减小了39.5%。此外还可以看出，优化后辊台速度的突变范围相比优化前大大减少。因此，可以推断，在添加一个合适K值的弹簧后，该装置受到速度和加速度突变带来的冲击得到了很大改善，并且运动过程更加平缓，提高了其稳定性，并有助于延长机构的使用寿命。

5 结语

根据实际生产需要，本文首先建立了辊台翻折机构三维模型，发现机构具有确定运动。随后通过受力分析，确定了关键部件气缸的型号，得到了推力大小。运用Adams软件对其进行动力学仿真分析，发现其在运动末端存在冲击较大的问题，并通过添加一个具有合适K值的弹簧对该问题进行了优化。

仿真结果显示，优化后，该翻折机构辊台的质心速度峰值相较于优化前减小了21.1%，质心加速度速度峰值相较于优化前39.5%，并且优化后速度和加速度达到峰值后的突变范围大大减小，对提高该机构的稳定性和延长使用寿命具有重要作用。此外，本文提出了使用Adams对结构进行动力学仿真与分析的方法，该方法可以有效提高设计开发的效率，为类似机械的优化设计提供了参考。