GNSS网基线检核对平差结果的影响

邢金玉 金 鹏 房大为 许永强

（1.河北省第一测绘院，河北 石家庄 050031；2.北京市测绘设计研究院，北京 100038；3.城市空间信息工程北京市重点实验室，北京 100038）

0 引言

在施测全球导航卫星系统（global navigation satellite system，GNSS）控制网时，通常是使用数量不等的GNSS 接收机在外业进行数据采集，采用随机软件下载观测数据并进行基线向量的解算，解算完毕后使用随机软件进行平差计算，或者从随机软件中导出基线解文件，使用经过国家认定的商用平差软件对GNSS 网进行平差计算，得到我们所需要的控制网的成果。

GNSS 控制网的误差来源主要包括三类：与卫星相关的误差、与大气传输相关的误差、与接收机相关的误差，在实际的作业过程中通常需要解决的是与接收机相关的误差，包括接收机安置误差以及观测误差［1］。

为确保GNSS 控制网测量成果的精度和可靠性，在相应的测量规范中，对于不同等级控制网的施测，其观测时段数、时段长度均有具体的规定，根据《全球定位系统（GPS）测量规范》（GB/T 18314—2009）10.1.2 的技术规定，C 级网的观测时段数≥2，时段长度≥4［2］。

GNSS 控制网的基本元素是GNSS 基线向量，因而基线向量质量的好坏对GNSS 控制网的质量有着直接的影响，在数据处理中，应该采用相应的质量控制措施，以确保其质量能满足规范和项目的要求，GNSS 基线的质量依赖于GNSS 观测数据的质量和基线处理方法。

基线向量解算完成后，评定基线解算结果质量的指标有两类，一类是基于测量规范的控制指标，另一类是基于统计学原理的参考指标。在工程应用中，规范的控制指标必须满足，而参考指标则不作为判别质量是否合格的依据［3］。

在平差过程中，虽然采用GNSS 同步观测的基线向量解作为观测量能消除各同步网位置基准的系统误差对平差结果的影响，但是采用坐标解作为平差的观测量进行平差得到的结果更能真实地反映控制网的实际精度水平［4］。

在除了剔除含有粗差的基线向量外，还需要对基线处理结果的质量进行检核，检核内容包括同步环闭合差、异步环闭合差以及重复基线边长较差的检核。

如果不进行这些检核就进行平差计算会对平差结果有多大的影响，下面就作业实例进行探讨。

1 作业实例

该C 级GNSS 网位于河北省南部，共联测控制点13 个，其中包含省级连续运行参考站（continuously operating reference stations，CORS）2 个（HDWX、XTLX），国家B 级控制点2 个（1179、1120），新建C 级控制点9 个，使用5 台Trimble R8进行外业数据采集，平均上站率≥2，采用随机软件TBC3.60 进行数据下载、基线解算与基线检核，使用武汉大学测绘学院研制开发的科傻数据处理系统（CosaGPS 5.21）进行控制网的平差计算，CORS 基准站的起算坐标数据为自然资源部西安大地测量数据处理中心2011 年平差出来的最新成果。控制网观测网如图1所示。

图1 测量标志重建C级GNSS观测网

基线解算采用随机软件TBC3.60，解类型设置为固定，频率使用多频，水平精度标志设置为0.050 m+1.0×10-6D，D为相邻点间距离（km），垂直精度标志设置为0.100 m+1.0×10-6D。

在数据统计分析中，将所有值平方求和，求其均值后再开平方，就得到均方根（root mean square，RMS）的数值，常用RMS值来分析噪声。

RMS 是观测值中噪声的量度，通常认为RMS值越小越好。要达到“通过”状态，RMS 值必须小于“标记”值，虽然RMS检验包含单频标记和失败域以及双频标记和失败域，但本次作业选择的是双频标记和失败域作为检验项，标记值设置为：0.005 m+0.5×10-6D［5］。

相对定位是指在观测值间求差并利用求差后的差分观测值进行定位，在相对定位中常用双差观测值求解基线向量，由双差观测值列出误差方程式，然后利用最小二乘平差原理求解基线向量，基线向量的解算是一个复杂的计算过程，实际处理时要顾及时段信号间断引起的数据剔除、劣质观测数据的发现及剔除、卫星变化引起的整周未知参数的增加等问题。

基线解算完成后进行了基线检核，基线检核设置环的边数为3 条，固定误差设置为5 mm，比例误差系数设置为1×10-6D，判定合格与不合格的标准为环闭合差Ws以及坐标分量闭合差WX、WY、WZ均不能超限，基线检核结果统计如表1所示。

表1 基线检核统计表

通过表1 看出，只有同步环闭合差有不合格的情况出现，这也与同步环闭合差限差要求严格相对应，表2 是对不合格的同步环超限情况的统计。

表2 同步环超限情况统计表

从表2 中看出，坐标分量闭合差WZ不合格的最多，为8 个，6 个不合格的环闭合差WS中有1 个是由Wx直接 引起（序号12），1 个是由Wy和WZ引起（序号2），3 个是由WZ直接引起（序号1、3、7），剩余1个是由Wx、Wy、WZ三者共同作用引起的（序号10），另外有3 个WZ虽然不合格（序号4、5、6），但并未造成Ws的不合格。

鉴于WZ不合格数量最多，因此在外业作业中精准设置仪器以及准确量取天线高度很有必要。

接收机天线相位中心相对测站标石中心位置的误差叫接收机位置误差。这里包括天线的置平、对中不精准引起的误差和量取天线高误差。如当天线高度为1.6 m 时，置平误差为0.1°时，可能会产生对中误差3 mm，因此，在精密定位时，必须仔细操作，以尽量减少这种误差的影响。在变形测量中，应采用有强制对中装置的观测墩［6］。

除了上面提到的接收机位置误差或者叫安置误差外，另外一种与接收机误差叫观测误差，为提高精度，应使位置精度因子（position dilution of precision，PDOP）值尽可能小，这就是说，应选择由用户位置和卫星位置构成的四面体的体积为最大的一组卫星进行观测［7］。

1.1 使用所有基线向量平差计算

用多台接收机进行多次观测，就形成一个由GNSS 基线向量组成的GNSS 网，网中包含地面起算数据和观测数据，这就产生了GNSS 网与地面数据的三维联合平差，地面观测值可按公式列出它们的误差方程，建立了全部基线向量的误差方程后与地面观测值的误差方程联合组成法方程，就可以解出各点的大地坐标和转换参数的平差值［8］。

基线向量解算完成后，不进行基线检核，即不考虑同步环闭合差不合格的情况下导出基线向量文件，使用全部基线向量进行GNSS网平差。

首先固定一个CORS 站的三维坐标进行三维无约束平差，GNSS 网中含有许多闭合条件，通过三维无约束平差可消除闭合条件的不符值，并建立网的基准，即网的位置、方向和尺度基准。基线向量本身已经确定了方向和尺度基准，与网的平差方法无关，而网的位置基准则与平差的方法密切相关。

三维无约束平差的目的是考察网本身的内符合精度以及考察基线向量之间有无明显的系统误差和粗差，同时为GNSS 大地高与公共点正常高联合确定GNSS 网点的高程异常，提供平差处理后的大地高程数据［9］。

在三维无约束平差结果中，三维基线向量的残差均合格，其中最弱边为HDWX-C464，其边长相对中误差为1/3 090 000。

三维约束平差基本方法为建立包含地心系到参心系的转换参数和参心系下坐标参数在内的统一函数模型，平差后可直接得出待定点在参心系下的坐标。

固定两个CORS 站的坐标进行三维约束平差，两个B 级点作为校核点，在平差结果中，三维基线向量残差均合格，其中最弱边为HDWXC464，其边长相对中误差为1/2 986 000，最弱点为C460，其点位中误差为Mp=1.84 cm，其坐标分量中误差分别为Mx=0.69 cm，My=1.31 cm，Mz=1.09 cm。

1.2 使用检核后的基线向量平差计算

由于有12个三边同步环是不合格的，所以只对组成不合格同步环的基线向量进行重新计算或删除，经过反复计算，最后得到的基线检核结果如表3所示。

基线是相关的，基线间的相关性对解算结果是有影响的，基线间的这种相关性容易造成粗差的转移和隐藏，所以对于高精度GNSS 网的数据处理，必须考虑基线间的相关性，不合格的基线应该在平差前剔除出去［10］。

由表3看出，正是由于删除了部分基线向量，造成了合格的同步环、异步环以及重复基线的数目都有不同程度的减少，其中异步环减少的最多，导出基线向量文件进行平差计算，固定的点和平差过程与首次的计算完全相同。

三维无约束平差结果中，三维基线向量残差均合格，其中最弱边为HDWX-C466，其边长相对中误差为1/6 469 000；在三维约束平差结果中，三维基线向量残差均合格，其中最弱边为HDWX-C466，其边长相对中误差为1/6 236 000，最弱点为C460，其点位中误差为MP=2.03 cm，其坐标分量中误差分别为Mx=0.76 cm，My=1.45 cm，Mz=1.20 cm。

2 比较与分析

根据上面的平差计算成果，可以通过对比发现两次平差结果的差异，并对产生差异的原因进行分析。

2.1 平差结果比较

由于两次平差所采用的基线向量不同，造成最弱边不是同名基线，对最弱边的比较已经没有意义，所以我们只对点位精度进行比较，首先比较两次平差后坐标成果的差值，差值为首次平差结果减去第二次平差结果，见表4。

表4 两次平差成果坐标较差表 单位：m

由表4可以看出，在空间直角坐标系中，C464坐标较差最大，为0.008 m，C459 坐标较差最小，为0.001 m，均值为0.004 m。在平面直角坐标中，较差最大与最小的点也是该两个点，同时C462、C460、1120是较差最小的点。

以空间直角坐标的点位精度来比较两次平差结果精度的不同，未进行基线检核，选取所有基线向量的基线解文件进行平差计算，点位精度如表5所示。

表5 首次平差点位精度表 单位：cm

进行基线检核后提取基线解文件进行平差计算，平差的设置与第一次一样，平差报告中精度评定中点位精度情况见表6。

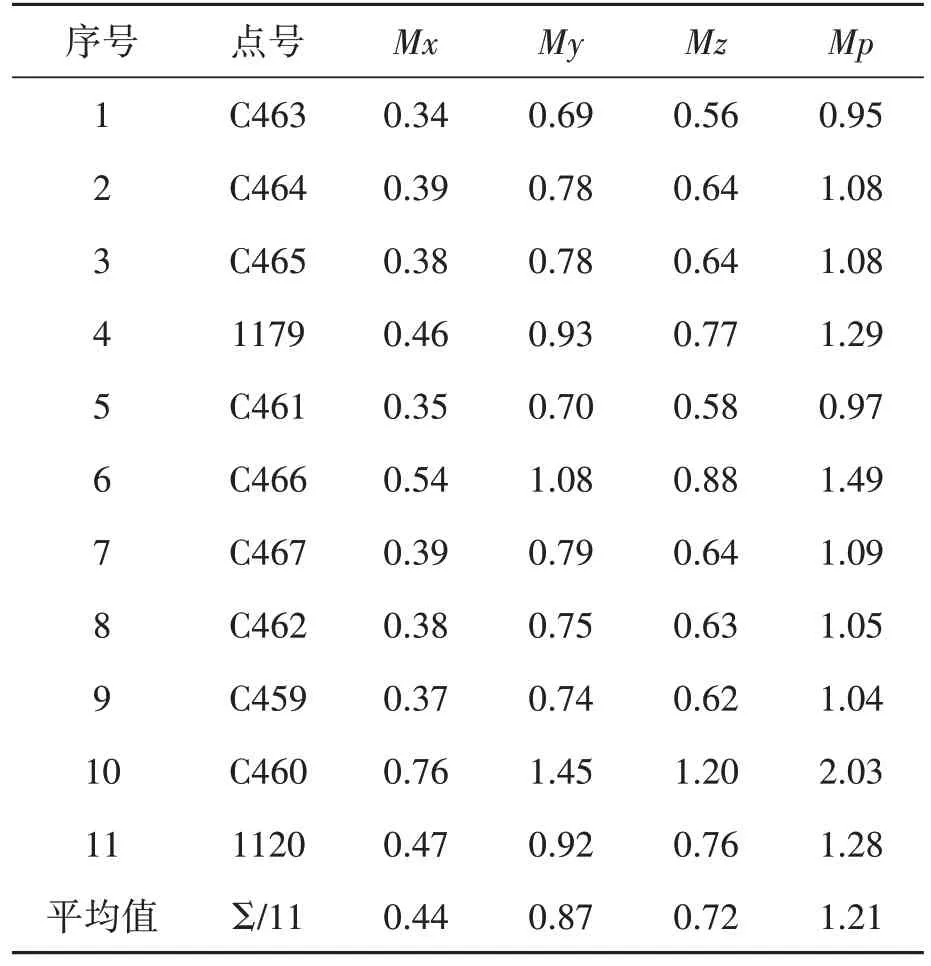
表6 二次平差点位精度表 单位：cm

通过对表5、表6 两个表格的对比，发现进行基线检核后的平差结果中除了1179、C461、C459三个点的精度略有提高外，其他8 个点的点位精度反而都降低了，什么原因造成了这种结果，是本研究需要探讨的问题。

2.2 原因分析

既然使用全部基线向量进行平差的结果点位精度更高一些，是不是就应该选取全部基线向量进行平差计算，而不需要进行基线检核了呢。

由表4 可知，两次平差结果中的空间直角坐标较差均值为4 mm，平面直角坐标的坐标较差均值为3 mm，两次平差的结果虽然无明显变化，但是差距也不容忽视。

点位中误差虽然可以用来评定待定点的点位精度，但是它却不能代表该点在某一任意方向上的误差大小，为了便于求定待定点点位在任意方向上误差的大小，一般是通过求出待定点的点位误差椭圆来实现的，这样就可以比较精确地、形象而全面地反映待定点在各个方向上误差的分布情况。

这说明点位中误差在反映控制网的精度方面有一定的局限性，在《全球定位系统（GPS）测量规范》（GB/T 18314—2009）里面“级别划分和测量精度”一节中对C 级网的精度要求为其相对精度应不低于1×10-6，并无点位中误差精度方面的相关要求。

精度评定需要首先得到单位权中误差，无论是条件平差还是间接平差，单位权中误差的公式均为

式中，p为某一个观测值的权；v为某一个观测值的改正数；n为观测值个数；t为未知数个数［11］。

由两次平差结果中提供的基本信息可以验算单位权中误差，表7 是两次三维约束平差结果中提供的控制网的一些基本信息。

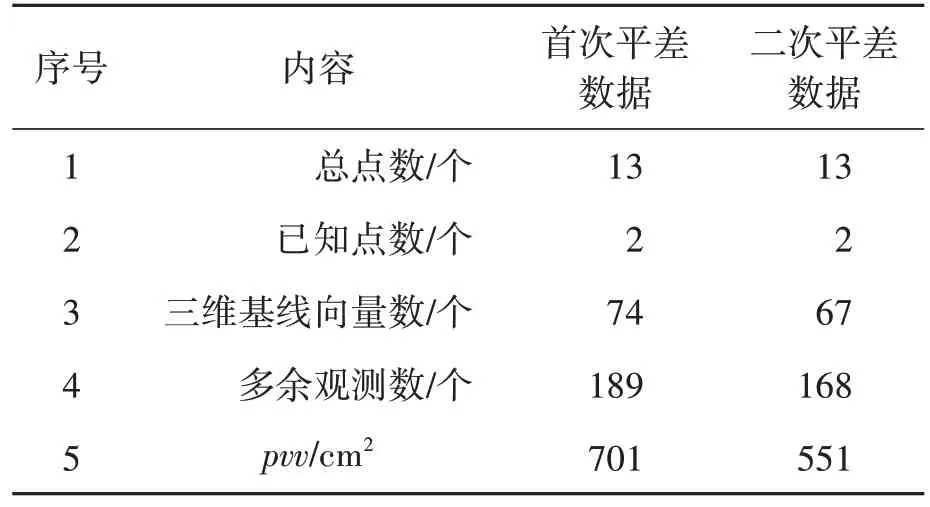
表7 控制网基本信息表

根据式（1）计算出两次平差的单位权中误差，对于一个确定的网来说，按最小二乘原则平差后，所得改正数v与所用平差方法无关，所以，无论GNSS 网平差取何种方法（经典平差法、伪逆平差法或拟稳平差法），其原始观测量的单位权中误差的计算公式是一样的［12］。

通过计算两次平差的单位权中误差分别为σ1=±1.927 cm、σ2=±1.811 cm。

可以看出，第二次平差的单位权中误差更小一些，说明第二次的平差精度要高于首次的平差，为什么第二次平差的点位精度更高一些呢，GNSS网平差后，其坐标分量中误差可按式（2）估算。

式中，σ0为单位权中误差；qxx、qyy、qzz、为权系数阵QXX、QYY、QZZ主对角线的相应元素，其坐标中误差可按式（3）计算。

权系数阵与所采用的平差方法密切相关，采用不同的平差方法其计算公式也不相同，权系数阵包含了所有平差量及其函数的精度信息，所以它对于平差后网的精度评定，具有极为重要的意义［13］。

由于首次平差比第二次平差多出21 个多余观测量，也就是增加了21 个函数相关观测，增加了多余观测量的点其首次平差求得的qxx、qyy、qzz比第二次平差要小，造成了未采取基线检核就进行平差反而得到了更高的点位精度。但并不是所有的点都增加了多余观测，这也是首次平差中仍有三个点精度低的原因，尽管如此增加的多余观测量还是提高了多数点的点位中误差的精度，造成了未采取基线检核就进行平差反而得到了更高的点位精度，出现了选取所有基线向量平差会出现点位中误差虚高的现象［14］。

点位坐标中误差是由两部分组成，一是单位权中误差，二是坐标分量的协因数阵，通常情况下增加了多余观测会造成此项变小，但增加了多余观测并不一定能使单位权中误差变小，因为式（1）中虽然n-t变大了，但pvv同样也变大了，因此同一个网采用不同的基线向量进行平差时，应以单位权中误差作为衡量网精度大小的一个重要指标，而不只是参照坐标的点位中误差，如果得到的单位权中误差比较小，甚至可以抵消协因数阵变大带来的影响，使得点位中误差也变小。

因此控制网平差前的基线检核还是很有必要的，基线检核会把外业观测数据中的粗差和误差超限部分剔除了，在国家标准和规范中对外业数据质量检核也做了相应的规定，特别是在卫星定位城市测量技术规范里面，关于“城市GNSS 控制网建设”中对GNSS 网基线解算有着更为严格和详细的规定［15］。

3 结束语

理论上GNSS 闭合环的各分量闭合差以及环闭合差是为零的，因此在各类规范中对基线检核都有相应的规定；在基线检核中异步环闭合差以及重复基线较差比较容易达到规范的要求，同步环闭合差容易出现不合格的情况；不合格的同步环中，坐标分量闭合差WZ不合格较多，许多环闭合差Ws不合格的原因也是由WZ不合格造成的，因此外业需要精准量取天线高；虽然选取所有的基线向量进行平差计算，有时会得到虚高的点位中误差，但进行基线检核还是很有必要的，也是应该必须进行检核的。