基于分布式降噪正交自编码器的工业过程故障检测

郭小萍 张玲 李元

基金项目：国家自然科学基金项目（批准号：61673279）资助的课题；2020年辽宁省教育厅科学研究经费项目（批准号：LJ2020021）资助的课题。

作者简介：郭小萍（1972-），教授，从事基于数据驱动的复杂过程诊断和质量预测的研究，Gxp2001@sina.com。

引用本文：郭小萍，张玲，李元.基于分布式降噪正交自编码器的工业过程故障检测[J].化工自动化及仪表，2023，50（6）：000-000.

DOI：10.20030/j.cnki.1000-3932.202306000

摘  要  针对基于过程知识进行模块划分的方法，存在知识不足造成模块划分不准确以及数据中的噪声导致的过拟合影响到故障检测率的问题，提出一种变量模块划分并采用降噪正交自编码器建立分布式故障检测的方法（MBIDOAE）。首先利用互信息和最短距离的层次聚类将相关关系强的过程变量聚类，获得多个模块。然后采用降噪正交自编码器提取各模块过程变量的非线性特征构建分布式模型，引入随机噪声来增强自编码器的抗噪性并利用正交矩阵降低特征的冗余性。采用T2和SPE统计量作为故障检测指标，通过对TE过程的仿真，与PCA、AE、MBIPCA和所提MBIDOAE进行对比，验证了该方法的有效性。

关键词  互信息  层次聚类  分布式建模  降噪正交自编码器  故障检测  冗余变量

中图分类号  TP277           文献标志码  A         文章编号  1000-3932（2023）06-0000-00

当今工业得到了蓬勃发展，与此同时现代工业生产的复杂程度也日益增加，因此故障的类型也会逐渐增多。而故障一旦发生，轻则影响工业生产的进程，造成生产效率降低，重则酿成安全事故。及时检测并定位出现问题的过程和设备，在酿成严重事故之前发出警报，从而使得工业生产过程中复杂系统的可靠性和安全性得到很大程度的提高，具有很高的应用价值[1，2]。但复杂工业过程变量众多且相互间有复杂的关系，过程局部发生的故障首先会对相关性强的变量有影响。因此，将过程变量划分模块，建立分布式故障检测有助于提高工业过程的故障检测率[3]。

主成分分析（PCA）和偏最小二乘法（PLS）

在过程检测领域得到了成功的应用[4]，但是工业生产过程中的变量并不总是线性的和高斯的，在大多数情况下，变量更多的是呈现出很强的非线性、非高斯，还有可能出现过拟合的情况，某些变量还会出现自相关的特性，此时上述两种方法的检测性能都会有所下降[5]。KRAMER M A提出用非线性PCA检测方法构造一个多层的神经网络模型[6]，但这种网络训练困难且泛化能力差。人工神经网络的出现针对这一问题提供了另一个崭新并且可行的方法，并且在数学层面上，该方法可以逼近一个任意的非线性函数。1986年自编码器（Auto-Encoder，AE）的概念被首次提出，并且在处理高维复杂数据的非线性问题上得到了成功应用[7]。YAN W W等提出了一种降噪自编码器的模型[8]，用于工业过程的故障检测，提高了模型的鲁棒性，在噪声干扰较多的情况下检测效果较好。ZHANG Z等针对高斯问题，提出一种基于变分自编码器的非线性故障检测方法[9]，有效获取了过程高斯特征信息，提高了故障检测效果。文献[10]采用正交自编码器的方法降低了输出特征的冗余性。

现代工业过程中存在许多变量，变量之间的相关性十分复杂，当个别变量发生改变导致局部故障发生时，将会存在众多冗余变量对故障检测造成干扰的情况。在采用全局建模策略的故障检测方法时，故障检测效果会降低。为了减弱冗余变量对检测的干扰，MACGREGOR J F等于1994年创新性地提出了基于多块建模策略的故障检测方法[11]，该方法首先将工业生产过程划分成几个模块，然后对这几个模块分别进行故障检测，最后融合现有的检测结果，有效地提高了对复杂过程的故障检测效果。WESTERHUIS J A等于1998年将多块PCA与PLS两种方法结合，并做出一定的改进，提出了新的方法[12]，首先对现有的变量进行划分，分成若干子模块，然后再借助标准PCA与PLS方法对子块建模。这些方法都是利用机理来划分子块，而在实际应用中，无法事先获得复杂工业过程的先验知识，因此上述两种方法在工业生产过程中的泛用性并不高。

互信息是一个随机变量中包含另外一个随机变量的信息度量[13]。这个测度指标具有很多的优点，如无参数、非线性等，目前，它已经在数据分析与建模领域引起了较多的关注[14，15]，此外，多变量统计故障检测领域方面的研究成果和进展，也有很多是通过借鉴互信息来分析处理过程数据的[16，17]。童楚东和史旭华针对多变量故障检测，提出一种基于互信息PCA的故障检测方法[18]，有效解决定义的相关矩阵局限于计算变量间的线性关系问题，实现了子块的自动划分。文献[19]利用互信息与层次聚类法，有效解决了建模过程的特征选择问题。

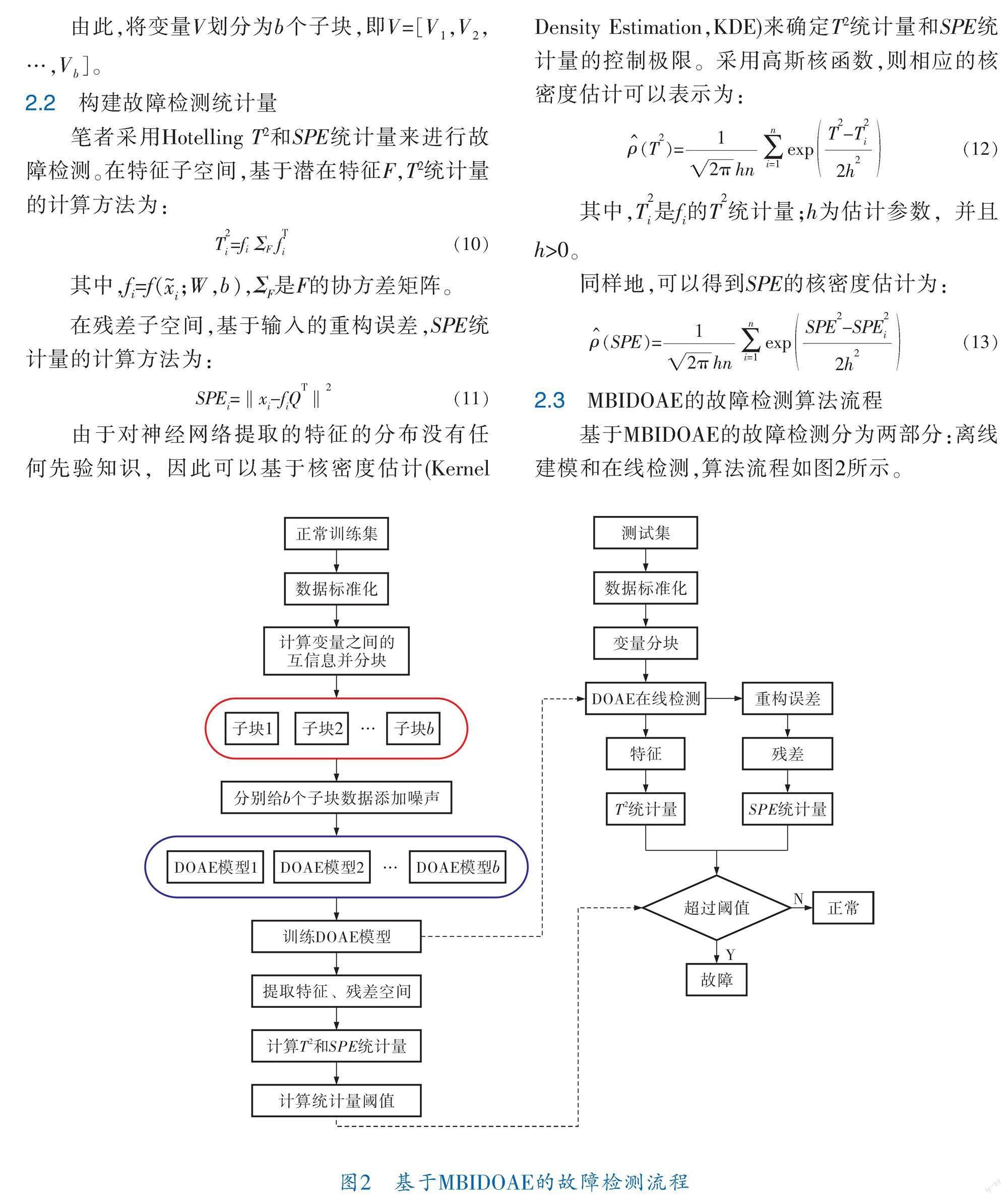
笔者提出一种基于分布降噪正交自编码器的工业过程故障检测方法，首先计算正常训练数据变量之间的互信息，然后采用最短距离层次聚类进行子模块划分。为了避免出现过拟合的情况，通过人为给原始数据添加噪声来增强自编码器的抗噪性。此外为了降低模型输出特征的冗余性，通过对自编码器算法加入正交矩阵，进而得到正交自編码器模型，然后建立降噪正交自编码器分布式检测模型提取非线性特征。对提取的特征计算统计量T2和SPE，将其作为故障检测指标，并用核密度估计法求出控制限。通过对TE[20]过程进行仿真，并与PCA、AE、基于多块信息的主元分析（MBIPCA）和基于分布式降噪正交自编码器（MBIDOAE）进行对比，验证了该方法具有更好的故障检测效果。

1  基本方法

1.1  互信息

互信息（Mutual Information，MI）是一种可以从熵的角度定量测量两个变量相互独立性的统计技术。MI是探索变量之间高阶相关性的有用工具，基于信息论，选取MI来衡量变量之间的相关性。变量x的香农熵表示为：

（1）

其中，p（x）为x的概率密度函数。熵值越高，表示不确定性越强，包含的统计信息越多。

由于变量间存在关联性，还需要计算两变量的联合熵，对于变量x1和x2，其联合熵的计算式为：

（2）

其中，p（x1，x2）为x1、x2的联合概率密度函数。由此，通过下式计算变量x1和x2的互信息：

（3）

展开后可得：

（4）

1.2  降噪正交自编码器

AE是一种常用的基于神经网络的无监督特征提取模型算法[21]，AE主要是由编码器φ和解码器ψ构成。AE试图学习一种可以以不同方式表示数据的映射函数，因此可以发现并利用初始数据。作为一种无监督学习算法，自编码器网络可以被视为3层，即输入层、隐藏层和输出层。输入层和输出层具有相同数量的节点，其目的在于最小化输入和输出之间的重构误差。编码器用于将输入数据X映射到低维特征空间，而解码器将低维特征空间中数据h映射为重构后的数据Y。为了增强抗噪性，通过在原自编码器的结构中，在输入信息中注入噪声，再使用含有噪声的“腐坏”样本重构无噪声的“干净”输入[22]。这就是降噪自编码器（Denoising Auto-encoder，DAE）的原理。研究发现通过对潜在空间施加正交约束能提高学习特征的独立性，因此又对自编码器的隐藏层添加约束，进而得到降噪正交自编码器（DOAE）模型，DOAE网络结构如图1所示。

假设具有n个样本的数据矩阵表示为X=[x1，x2，…，xn]?Rm×n，每个样本xi维度为m。通过修改自编码器的损失函数引入正交矩阵Q，进一步得到新的原始数据的主成分XQ并作为新的学习目标，将隐藏层提取的特征解码对XQ进行拟合。最后模型的优化目标即最小化自编码器输出值y与原始数据通过正交矩阵Q得到的主成分XQ之间的差值，模型的目标函数如下：

（5）

其中，自编码器的输出层为d维，f（xi；W，b）是d（d

由于QTQ=Id?d，目标函数变为以下形式：

（6）

由于目标函数非凸，并且Q与其他参数是相乘关系，难以同时计算。在求解的过程中先对Q进行初始化，然后通过反向传播法优化目标函数来得到最优的参数W、b：

（7）

加入正交性限制后，再对该模型的原始数据加入噪声来训练。降噪自编码器使用加入噪声的数据训练DAE网络以恢复真实输入，有较好的鲁棒性[23]。所以优化问题如下：

（8）

s.t. QTQ=Id?d

其中，为包含噪声的数据，=xi+，表示加入的高斯噪声。可以将式（8）写成如下形式：

（9）

s.t. QTQ=Id?d

其中，為包含噪声的原始数据，F?RN×d是建模数据的潜在特征。

2  基于MBIDOAE的故障检测方法

2.1  基于互信息的分块策略

笔者采用计算过程变量的互信息并采用凝聚型层次聚类进行子模块划分。该策略首先将两两变量计算得到的互信息作为一个簇，然后根据最短距离的合并准则逐步使得这些簇成为越来越大的簇，直到所有对象都在一个簇中，或者满足某个终止条件。

模块划分的主要步骤如下：

a. 对正常训练数据矩阵Xnor?Rn×m，计算两两属性之间的互信息，得到互信息矩阵Inor。

b. 将互信息矩阵Inor中的每个属性看作一个子块。

c. 将互信息矩阵中包含最大互信息值的两个子块根据最短距离的合并准则合并成一个新的子块，并将子块之间的互信息值置0。

d. 互信息矩阵有很多个子块，需要重复步骤c，直到全部子块合并为一个子块。

e. 根据子块合并记录，合并的子块是由两个多变量合并产生，则需要剔除合并中的单变量子块，直到当前的聚类结果为两个多变量子块合并产生。

由此，将变量V划分为b个子块，即V=[V1，V2，…，Vb]。

2.2  构建故障检测统计量

笔者采用Hotelling T2和SPE统计量来进行故障检测。在特征子空间，基于潜在特征F，T2统计量的计算方法为：

（10）

其中，fi=f（；W，b），ΣF是F的协方差矩阵。

在残差子空间，基于输入的重构误差，SPE统计量的计算方法为：

（11）

由于对神经网络提取的特征的分布没有任何先验知识，因此可以基于核密度估计（Kernel Density Estimation，KDE）来确定T2统计量和SPE统计量的控制极限。采用高斯核函数，则相应的核密度估计可以表示为：

（12）

其中，Ti2是fi的T2统计量，h为估计参数，且h>0。

同样地，可以得到SPE的核密度估计为：

（13）

2.3  MBIDOAE的故障检测算法流程

基于MBIDOAE的故障检测分为两部分：离线建模和在线检测，算法流程如图2所示。

离线建模的主要步骤为：

a. 标准化正常数据后，计算训练数据矩阵两两变量之间的互信息，得到互信息矩阵Inor。

b. 将互信息矩阵Inor中的每个属性看作一个子块，计算两两间的最小距离，将互信息值最大、距离最小的两个子块合并成一个新的子块，重新计算新的子块和所有子块之间的距离，重复此过程直到所有子块合并成一个子块，根据2.1节所述方法得到b个子块。

c. 为每个子块的原始数据添加高斯噪声生成数据。

d. 分别对每个子块初始化DOAE模型参数和正交矩阵Q。

e. 根据目标函数来训练模型，优化参数W、b。

f. 固定W和b，计算Q。

g. 利用模型提取出的潜在特征计算每个模型中的T2统计量，利用重构的残差空间计算每个模型SPE统计量。

h. 分别在每个模型里使用核密度估计法求T2和SPE控制限。

在线检测主要步骤为：

a. 对于测试样本，采用同样的方法进行标准化处理和分块处理。

b. 使用训练好的DOAE模型提取每个子块的特征和重构残差空间。

c. 计算每个模型的检测统计量T2和SPE。

d. 与控制限比较，若超出控制限，则判断过程发生了故障，反之则过程正常。

3  TE过程仿真研究

TE过程是一个典型的复杂工业过程，主要包括5个操作单元：反应器、冷凝器、循环压缩机、分离器和汽提塔，笔者选取52个变量用于建模和检测。TE过程共有21个故障工况，从第161次采样时间引入故障，用于训练模型和在线测试，每个数据集包含960个采样点。

针对正常训练数据，通过层次聚类将XMEAS（7）、XMEAS（9）、XMEAS（13）、XMEAS（16）4个变量剔除，确定出48个变量的子模块划分结果见表1，各子模块中包含变量数分别为14、29、5个。

采用PCA、AE、MBIPCA和笔者提出的MBIDOAE对故障14进行故障检测仿真实验，结果如图3～5所示，图中红线为控制限。该故障是关于反应器冷却水阀门的黏住问题故障，其与控制变量XMX（10）最相关，这些变量主要分布在子模块2中。

图3a是PCA方法检测结果，其可以检测出大部分的故障，但SPE的检测结果优于T2，SPE检测率是0.975 0，T2检测率是0.898 5。图3b是AE方法检测结果，T2检测率是0.985 0，SPE检测率是0.988 0。另外，PCA的T2误报率为0.025 0，SPE的误报率为0.037 50，AE的T2误报率为0.012 5，SPE的误报率为0.006 3，相比于PCA，AE有较好的检测效果和较低的误报率。

图4a～c为MBIPCA方法对3个子块的检测结果，子块1和3基本没有检测出故障，子块2检测出了故障，说明子块1和3变量正常，子块2变量有故障。另外，子块2的T2统计量检测率是0.988 8，SPE检测率是0.998 8，明确出该故障发生在子块2。

图5a～c为MBIDOAE方法对3个子块的检测结果，子块1和3基本没有检测出故障，子块2检测出了故障，说明子块1和3变量正常，子块2变量有故障。另外，子块2的T2统计量检测率是1，SPE检测率是1，其检测结果优于MBIPCA，明确出该故障发生在子块2。此外MBIPCA中的子块2的T2的误报率为0.025 0，SPE的误报率为0.012 5，而MBIDOAE的T2、SPE误报率均为0。进一步说明了MBIDOAE能明确故障发生的位置并且能检测出大部分来，同时在误报率上优于前3种算法。

为了进一步验证笔者所提方法的有效性，表2分别给出了几种方法对故障1的误报率和检测率。故障1是阶跃故障，与A、C进料比有关，通过分析得到与其相关性最大的变量为控制变量XMV（4），它是A、B、C进料，属于子块2。通过仿真结果比较，表明所提方法有更好的检测效果以及更低的误报率。

4  结束语

提出一种基于分布式降噪正交自编码器的工业过程故障检测方法，用于针对采用过程知识划分的方法，由于知识不足造成的模块划分不准确以及过程数据中有噪声从而影响故障检测率的问题。利用互信息和最短距离的层次聚类将相关关系强的过程变量聚类，获得多个模块。当训练过程中包含过多的噪声时会出现过拟合的情况，因此通过人为给原始数据添加噪声的方式来除去其中的噪声冗余。为了降低模型输出特征的冗余性，通過对自编码器算法加入正交矩阵，进而得到降噪正交自编码器模型，然后建立降噪正交自编码器分布式检测模型提取非线性特征。对提取的特征计算统计量T2和SPE，将其作为故障检测指标，并用核密度估计法求出控制限。通过TE过程进行仿真，将PCA、AE、MBIPCA和MBIDOAE进行对比，验证了MBIDOAE方法具有更好的故障检测效果。但该算法仅仅考虑检测过程的局部信息，对于数据之间存在的其他特征信息没有深究，今后将在该方面进一步研究。

参  考  文  献

[1] 刘强，卓洁，郎自强，等.数据驱动的工业过程运行监控与自优化研究展望[J].自动化学报，2018，44（11）：1944-1956.

[2] GE Z Q，SONG Z H，GAO F R.Review of recent research on data-based process monitoring[J].Industrial & Engineering Chemistry Research，2013，52（10）：3543-3562.

[3] PENG X，DING S X，DU W，et al.Distributed process monitoring based on canonical correlation analysis with partly-connected topology[J].Control Engineering Practice，2020，101：104500.

[4] 孟生军，童楚东.基于DPCA-IM的动态过程监测方法[J].计算机应用研究，2021，38（1）：175-178.

[5] GE Z Q，SONG Z H.Multivariate Statistical Process Control：Process Monitoring Methods and Applications[M].London：Springer Science & Business Media，2012.

[6] KRAMER M A.Nonlinear principal component analysis using auto associative neural networks[J].AIChE Journal，1991，37（2）：233-243.

[7] RUMELHART D E，HINTON G E，WILLIAMS R J.Learning representations by back-propagating errors[J].Nature，1986，323：533-536.

[8] YAN W W，GUO P J，LIANG G，et al.Nonlinear and robust statistical process monitoring based on variant auto encoders[J].Chemometrics and Intelligent Laboratory Systems，2016，158：31-40.

[9] ZHANG Z，JIANG T，ZHAN C J，et al.Gaussian feature learning based on variational auto-encoder for improving nonlinear process monitoring[J].Journal of Process Control，2019，75：136-155.

[10] 来杰，王晓丹，向前，等.自编码器及其应用综述[J].通信学报，2021，42（9）：218-230.

[11] MACGREGOR J F，JAECKLE C，Kiparissides C，et al.Process monitoring and diagnosis by multiblock PLS methods[J].AIChE Journal，1994，40（5）：826-838.

[12] WESTERHUIS J A，KOURTI T，MACGREGOR J F.Analysis of multiblock and hierarchical PCA and PLS models[J].Journal of Chemometrics：A Journal of the Chemometrics Society，1998，12（5）：301-321.

[13] LI W.Mutual information functions versus correlation functions[J].Journal of statistical physics，1990，60（5）：823-837.

[14] KWAK N，CHOI C H.Input feature selection for classification problems[J].IEEE Transactions on Neural Networks，2002，13（1）：143-159.

[15] HAN M，REN W，LIU X.Joint mutual information-based input variable selection for multivariate time series modeling[J].Engineering Applications of Artificial Intelligence，2015，37：250-257.

[16] VERRON S，TIPLICA T，KOBI A.Fault detection and identification with a new feature selection based on mutual information[J].Journal of Process Control，2008，18（5）：479-490.

[17] JIANG Q，YAN X.Plant-wide process monitoring based on mutual information multi-block principal component analysis[J].ISA Transactions，2014，53（5）：1516-1527.

[18] 童楚東，史旭华.基于互信息的PCA方法及其在过程监测中的应用[J].化工学报，2015，66（10）：4101-4106.

[19] 李欣倩，杨哲，任佳.基于互信息与层次聚类双重特征选择的改进朴素贝叶斯算法[J].测控技术，2022，41（2）：36-40；69.

[20] DOWNS J J，VOGEL E F.A plant-wide industrial process control problem[J].Computers & Chemical Engineering，1993，17（3）：245-255.

[21] 薛南，吕柏权，倪陈龙.基于自编码器和填充函数的深度学习优化算法[J].电子测量技术，2019，42（23）：79-84.

[22] CHUNG J，KASTNER K，DINH L，et al.A recurrent latent variable model for sequential data[J].Advances in Neural Information Processing Systems，2015，28（10）：99-100.

[23] 景军锋，党永强，苏泽斌.基于改进SAE网络的织物疵点检测算法[J].电子测量与仪器学报，2017，31（8）：1321-1329.

（收稿日期：2022-12-29，修回日期：2023-07-24）