基于RRT 算法的逆正向寻优路径规划

朱道扬

(武汉交通职业学院, 湖北 武汉 430065)

0 引言

根据对环境信息的把握程度可将路径规划划分为全局路径规划和局部路径规划。 全局路径规划需要采集地图信息来进行路径规划,传统算法有A*算法[1]、Dijkstra 算法[2]、快速扩展随机树(RRT)算法[3-5]等,这类算法对复杂空间和障碍物进行建模的精度直接影响搜索效率。 基于智能算法有遗传算法[6]、粒子群算法[7]、蚁群算法[8]等,此类算法虽然学习能力非常强,但实时性差、计算量大,需要占用大量的存储空间。 其中,RRT算法具有结构简单、概率完备性、强大的搜索扩展能力以及避免对复杂空间精确建模等优点被广泛运用于机器人的路径规划,然而现有的RRT 算法有着搜索效率低、易陷入局部极小值、路径不光滑等缺点。 北京工业大学的阮晓钢等[9]提出了一种基于信息增益与RRT 相结合的机器人环境探索策略,增强机器人对未知环境的探索,降低传统RRT 算法固有的盲目性,但是需要精确的空间建模且计算量较大。 广东工业大学的何兆楚等[10]利用人工势场法与RRT 算法结合避免陷入局部极小值,但是全局路径不是最优。 谭波等[11]对搜索路径的节点进行修剪,利用B 样条曲线得到光顺路径,但是修剪节点常常不能取得满意的结果,导致全局路径不最优。

针对原始RRT 算法存在全局规划路径不最优、路径平滑性差的问题,本文提出一种改进RRT 算法,该算法首先对原始RRT 算法的规划路径进行逆向寻优,减少路径规划的长度和节点数,然后再对该路径进行正向寻优,避免规划路径陷入局部最优,实现规划路径的全局优化,最后通过在4 种地图环境下对3 种算法进行100 次路径规划仿真实验验证本算法的可靠性和有效性。

1 RRT 算法基本原理

LaValle 于1999 年首次提出快速扩展随机树(RRT)算法, 优势在于无需对系统进行建模,无需对搜索区域进行几何划分,搜索空间的覆盖率高,搜索的范围广,可以尽可能地探索未知区域。在采样空间内确定起点和目标点,通过随机采样扩展增加新节点,生成一个随机扩展树,当随机树中的新节点包含目标点或进入目标区域时,初始点到目标点间至少形成一条以随机树新节点组成的路径。

从理论上看,RRT 算法是一种具有概率完备性的全局路径规划算法,只要迭代足够多的次数就一定能保证找到一条从起点到目标点的路径。 同时,RRT 算法不需要对环境进行具体的建模,只需要确定障碍物的位置坐标和抽象后的位姿信息,因此预处理的数据量相对较少。但是在实际应用中发现,基本的RRT 算法存在以下缺点。

1) 搜索效率低: 由于RRT 算法是对全局路径进行规划,虽然具有完备性的优点,但是针对目标的搜索效率较低,造成计算量较大。

2) 全局路径不最优:搜索的路径由众多节点组成,其中许多节点为无效节点,造成规划路径蜿蜒曲折,因此不能保证每次规划路径最短。

3) 路径平滑性不足:节点与节点之间通过直线连接,所规划路径的各段直线之间存在较多拐角,缺乏平滑性,难以满足机器人运动的平稳性要求。

2 改进RRT 算法

为了实现RRT 算法规划路径的全局寻优,本文提出了一种逆正向寻优的方法来改进RRT 算法的规划路径,如图1 所示。 逆正向寻优方法充分应用两点之间线段最短的数学思想,达到缩短路径长度的目的。 图中X1为起点,X11为终点,原始的RRT 算法扩展产生的节点为Xi(i=2…11),黑色区域表示障碍物,蓝色实线表示原始的RRT算法初步生成的搜索路径,用X11到X1的黄色虚线表示逆向寻优路径,用X1到X11的红色点线表示在逆向寻优路径后使用正向寻优产生的路径。经过验证,当节点数量太多,可以重复上述逆正向寻优算法,但是一次逆正向寻优可以避免多数规划路径陷入局部极值,多次逆正向寻优只会使路径规划质量略有提升,反而会使路径寻优内存消耗显著增加。

图1 逆正向路径优化

改进后的RRT 算法伪代码如表1 所示,具体优化过程如下。 首先在起点X1与终点X11直接生产RRT 的规划路径,然后逆向寻优规划路径,从终点X11搜索并连接最近的父节点X9、X8、X7……X1,依次形成逆向规划路径X11—X9、X11—X8、X11—X7、X11—X6、……X11—X1,只要检测到逆向规划路径有障碍物存在,就把该路径节点的上一父节点存储起来。 例如,在检测逆向规划路径X11—X9没有障碍物,但是在检测逆向规划路径X11—X8有障碍物,则把X11、X9作为父节点存储起来,接着从X9继续形成逆向规划路径X9—X8、X9—X7、X9—X6、X9—X5、……X9—X1,并检测是否有障碍物,同样把碰撞点的前一个父节点存储起来,因此,下图中逆向寻优路径可以找到父节点X11、X9、X6、X4、X3、X2、X1。 可以看出逆向寻优虽然可以对规划路径全局寻优,但是仍然有部分节点(X4、X3、X2、X1)陷入局部极值,因此,在逆向寻优路径后进行一次正向寻优,可以解决上述问题。从起点X1出发寻找碰撞点的前一个父节点,可以找到父节点X1、X4、X6、X9、X11。 当整个路径完成优化时,得到如图1 所示的正向寻优路径,即算法结束。

表1 逆正向寻优RRT algorithm

3 仿真验证

将原始的RRT 算法、逆向寻优RRT 算法、逆正向寻优RRT 算法在MATLAB 中做仿真实验。在二维仿真栅格地图环境下进行全局路径规划对比验证,仿真地图分为单个障碍物、单个狭窄通道、简单环境和复杂环境4 个不同的场景,仿真地图尺寸均为1000×1000 像素的格栅表示,左上起点坐标为(100,-100),右下目标点坐标(900,-900),目标点阈值为50,搜索允许扩展最大步长为30。 在4 种环境下每种算法进行200 次重复实验,并统计算法各个指标的平均值。 如图2—5 所示,图中左上角红点表示起点,右下角绿色点表示目标点,红色树状分支表示扩展节点,蓝色实线表示RRT 算法规划路径,绿色虚线表示逆向寻优规划路径,黑色点线表示正向寻优规划路径。

图2 单个障碍物环境下的算法效果对比

3.1 单个障碍物情况

在单个障碍情况下,3 种算法路径规划效果如图2 所示。 原始RRT 算法规划出的路径节点较多,光滑性很差,路径长度不是最优或者次优;逆向寻优后的规划路径大大减少了RRT 算法节点数量,路径节点数目为3 个,路径长度缩短,路径质量显著提高;对逆向寻优后的规划路径再次进行正向寻优,其效果基本和逆向寻优效果相同,说明逆向寻优后的RRT 算法足以满足简单场景下的路径规划。

3.2 单个狭窄通道

在单个狭窄通道情况下,3 种算法路径规划效果如图3 所示。 原始RRT 算法依然可以找到规划路径,规划出的路径节点很多,光滑性很差,路径长度不是最优;逆向寻优后的RRT 算法路径节点数量明显减少,多次实验得到路径节点数目为4 个,路径规划质量有所改善;对逆向寻优后的规划路径再次进行正向寻优,其效果基本和逆向寻优效果相同,说明逆向寻优后的RRT 算法同样可以满足此类场景下的路径规划。

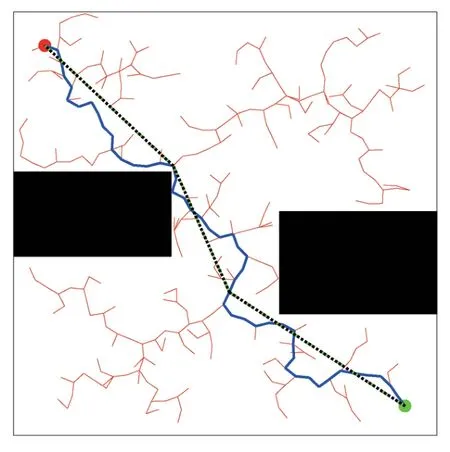
图3 单个狭窄通道环境下的算法效果对比

3.3 简单环境

在简单环境情况下,3 种算法路径规划效果如图4 所示。 由于RRT 算法的全概率采样特点,在此种障碍物较多的情况下,依然可以找到规划路径,其路径光滑性也较差;逆向寻优后的RRT算法改变了父节点的选取,规划出的路径长度有所降低,路径节点数目为7,光滑性相对较好,但是仍存在局部路径节点选取不是最优的情况,如图中左下角路径节点未合理优化;正向寻优可以避免逆向寻优陷入局部最优的问题,实现规划路径的全局寻优,其路径节点只有6 个,路径长度减少,路径光滑性会有所提高。

图4 简单环境下的算法效果对比

3.4 复杂环境

在复杂环境情况下,3 种算法路径规划效果如图5 所示。 RRT 算法依然可以找到规划路径,其路径同样较为曲折,光滑性也非常差;逆向寻优后的RRT 算法改变了父节点的选取,寻优后的规划路径平均长度显著降低,规划路径平均节点数目为23,光滑性相对较好,但是仍存在局部路径节点选取不是最优的情况,如图中左上角有两处路径节点未合理优化;再经过正向寻优后规划路径平均节点只有20 个,路径拐角减少,路径光滑性会有所提高。

图5 复杂环境下的算法效果对比

为了便于进一步和原始RRT 算法的相关数据进行比较,验证逆向寻优RRT 算法、逆正向寻优RRT 算法有效性与可靠性,在相同条件下对以上4 个不同的场景重复进行100 次路径规划实验,计算3 种算法的规划路径平均路径长度和平均节点数目,结果如表2、3 所示。

表2 规划路径平均长度

由表2 可知,在单个障碍物环境下,原始RRT算法路径平均长度为1523.5 mm,后两种算法的规划路径平均长度分别为1215.2 mm、1204.4 mm,比原始RRT 算法在规划路径平均长度上分别减少20.24%、20.95%;在单个狭窄通道环境下,原始RRT 算法规划路径平均长度为1536.6 mm,后两种算法的规划路径平均长度分别为1181.9 mm、1176.6 mm,比原始RRT 算法的规划路径平均长度分别减少23.08%、23.43%;在简单环境下,原始RRT 算法规划路径平均长度为2159.3 mm,后两种算法的规划路径平均长度分别为1636.7 mm、1596.4 mm,比原始RRT 算法规划路径平均长度分别减少24.20%、26.07%;在复杂环境下,原始RRT 算法规划路径平均长度为2983.2 mm,后两种算法的规划路径平均长度比原始RRT 算法规划路径平均长度分别减少了19.16%、20.20%。 因此,在4 中环境下逆正向寻优后的RRT 算法在规划路径寻优上性能最佳。

由表3 可知,在单个障碍物环境下,原始RRT算法规划路径平径节点数为51.48,后两种算法的规划路径平均节点数分别为3.08、3.04,比原始RRT 算法的规划路径平均节点数减少94.02%、94.09%;在单个狭窄通道环境下,原始RRT 算法规划路径平均节点数为51.95,后两种算法的规划路径平均节点数分别为4.04、4.02,比原始RRT 算法的规划路径平均节点数减少92.22%、92.26%;在简单环境下,原始RRT 算法规划路径平均节点数为76.68,后两种算法的规划路径平均节点数分别为7.55、6.35,比原始RRT 算法的规划路径平均节点数减少90.15%、91.72%;在复杂环境下,原始RRT 算法规划路径平均节点数为100.3,后两种算法比原始RRT 算法的规划路径平均节点数减少77.57%、79.66%,在4 种环境中,依然是逆正向寻优后的RRT 算法性能最佳。

表3 规划路径平均节点数

4 结论

针对原始RRT 算法存在全局规划路径不最优、路径平滑性差的问题,本文提出了一种改进的RRT 算法,该算法首先对原始RRT 算法的规划路径进行逆向寻优,然后再对该路径进行正向寻优,通过在4 种地图环境下对3 种算法进行100 次路径规划实验。 仿真结果表明,与原始RRT 算法相比,改进的算法的有效性和可靠性主要体现在以下几个方面。

1) 与原始RRT 算法相比,逆正向寻优后的RRT 算法进行路径规划所需的平均路径最短,路径长度减少了19%以上。 通过对比上述4 种环境,逆正向寻优后的RRT 算法性能提升幅度都是最大。

2) 与原始RRT 算法相比,逆正向寻优后的RRT 算法进行路径规划所需的平均节点数最少,节点数减少了70%以上。 通过对比上述4 种环境,逆正向寻优后的RRT 算法性能提升幅度都是最大,且随着环境复杂程度的增加,逆正向寻优后的RRT 算法性能会依次降低。

3) 与原始RRT 算法相比,逆正向寻优后的RRT 算法规划路径的平滑性有显著改善,规划路径的拐角减少,其能够更好地满足机器人运动的要求。

4) 本文所提出的改进RRT 算法虽然可以搜索路径的全局寻优,但是无法得到最短路径;规划路径拐角的平滑性还需进一步优化;规划路径太过靠近障碍物等,上述缺点也是今后的重点研究方向。