基于GWO-SVR斜拉桥结构可靠度分析

张 硕 许志南

（1.辽宁石油化工大学，辽宁 抚顺 113001；2.中国建筑第八工程局第二建设有限公司，北京 101100）

0 引言

在交通基础设施的设计过程中，桥梁结构的安全性设计显得尤为重要。现代桥梁结构在形式上不断创新，斜拉桥的组成形式较为复杂，其主要由桥塔、斜拉索、主梁三个部件构成[1]，以其柔度大、自重轻、弹性支承多为主要特点。除斜拉桥结构所采用的材料及其外观形状等固有特性外，外部的随机风荷载对斜拉桥结构也会产生较大的影响。因此，这些因素的随机性都是斜拉桥结构可靠度计算过程中需要重点考虑的问题。

可靠度是用来评价结构在规定时间和规定条件下完成预定功能的概率指标。通过数学方法对结构在其正常服役期间的失效风险进行量化处理，转化为可靠度指标，用于结构后续服役过程中的管养及结构寿命预测。

本文利用支持向量回归（Support Vector Regression，SVR），将其惩罚因子及核函数进行优化，对单塔型斜拉桥结构进行可靠度预测。

1 基本原理

Vanpid 提出了一种基于监督式学习的机器学习方法，即支持向量机（SVM），见图1所示，在统计分类问题和回归分析计算中得到了普遍应用[2]。支持向量机比其他统计学习理论方法具有更多优势，在样本量不足的情况下，支持向量机[3]的学习能力和泛化能力也要优于其他方法。

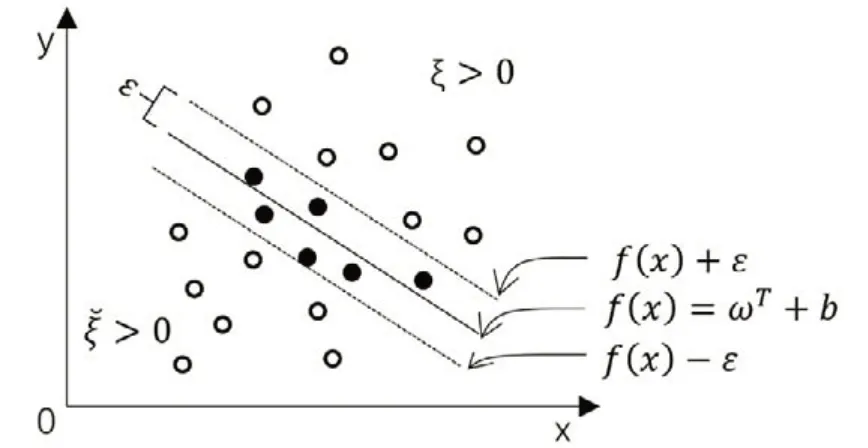
图1 支持向量机

基于结构风险最小化[4]的原则，构建超平面是支持向量机用于数据分类的主要方式，假定包含M个数据的训练集利用超平面ωT+b=0将训练集数据进行分类。

用xa和xb表示正负两个方向的支持向量，支持向量满足yl(ωTxl+b)=1，则超平面到最近样本点的几何间距为2/‖ ‖ω，支持向量问题变为最优化问题，目标优化函数表达为最小值的形式为：

2 支持向量回归

预测值与真实值没有误差时，预测损失才为零，这样的预测方式容易出现过拟合的情况。因此，SVR过程中设置了一个宽度为2ε的“软间隔”，ε为不敏感损失因子，只有预测值与真实值的误差超过了ε时才开始计算预测误差。SVR的目的是使(+ε,-ε)外的样本点距离该“软间隔”的距离最大，同时使(+ε,-ε)内的距离最优超平面最远的样本点与最优超平面的距离最小，因此SVR可以用下式表达：

其中，惩罚因子为C，ε的不敏感损失函数为Uε。

由于不敏感损失函数Uε存在绝对值，因此对其进行转化，定义两个大于零的松弛变量ξ，。通过惩罚因子C控制ξl，l的偏差量，确保支持向量回归不会因为松弛变量过大出现欠拟合的情况。同时将支持向量回归的目标函数构造为Lagrange函数，可以表示为：

3 参数选择

惩罚因子C用于控制样本点的离散界限，而核函数使低维空间的样本通过某种映射方式映射到高维空间，核函数中的参数取值影响了样本点在高维空间的映射效果。在常见的支持向量回归核函数中，只有高斯径向基核函数仅包含一个参数，且高斯径向基核函数可以确保映射到高维空间中的样本数据可以线性分类，因此本文回归过程中的核函数选用高斯径向基核函数。

为了寻找惩罚因子C和核函数参数g的最优取值，学者们采取了多种优化算法。传统的参数优化方法往往存在耗时长、泛化能力差等缺点。灰狼优化算法（GWO）是近年来由Seyedali Mirjalili 等人提出的一种群体智能算法[5]。与其他优化算法相比，GWO需要调整的参数较少，结构组成简单，容易实现。因此本文选用GWO 来进行SVR中的参数寻优，建立一种GWO-SVR的结构代理模型，提升模型性能。

4 灰狼优化

GWO在空间中随机产生灰狼种群，并将其按照个体适应度分别划分为α，β，δ三个等级，剩下的群体为ω。以围捕、狩猎、进攻三个阶段划分狼群捕猎过程，最终获取全局最优解，各个过程描述如下：

4.1 围捕

灰狼种群在捕猎时的首要行为是包围猎物，用数学模型表达该行为如下：

4.2 狩猎

在狼群包围目标猎物后，ω狼群会在α狼，β狼，δ狼领导下狩猎，每次迭代过程中保存α，β，δ的位置信息，狼群根据领导狼的位置数据更新自身所处位置，用数学模型表达该行为如下：

4.3 攻击

确定猎物位置后，对猎物发起攻击，攻击猎物确定猎物位置，即得到数学模型的最优解，攻击过程通过迭代实现，迭代过程中收敛因子a→从2递减至0，迭代结束后获得全局最优解[6]。

5 有限元建模

本文利用有限元软件ANSYS建立一个单塔斜拉桥结构的有限元分析模型。在该模型中，斜拉索则采用LINK180杆单元，索塔和主梁采用BEAM188结构单元，桥面板采用SHELL181单元。该斜拉桥的全长为264m。全桥共计节点1588个，关键点169个，划分单元2422个。斜拉桥成桥状态下模型如图2。

图2 “斜拉桥成桥状态下”模型

按照《桥梁抗风设计规范》[7]的要求，在标准高度10m处选择50年一遇的最大风速。极值风速定为30m/s。选定kaimal风速谱为脉动风速谱，运用谐波合成法，模拟所需风速时程并将其转换为荷载。选取300s内最大荷载值作为随机变量，与材料参数等其他影响斜拉桥可靠性的主要因素，组成可靠度计算的随机变量，取值如表1所示。

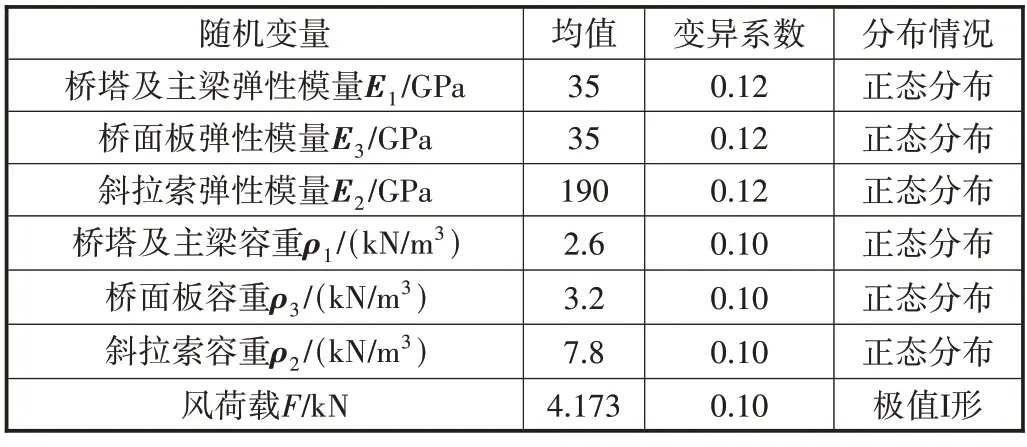
表1 影响斜拉桥可靠性分析表

拟定随机变量为7个，选取60组样本点，其中45个为训练集，剩余15组作为测试集，根据各个随机变量的均值及其方差运用LHS抽样法在[3,3]范围内进行抽样，将抽样数据载入ANSYS有限元模型，计算出斜拉桥在风荷载加载条件下的输出数据X，即斜拉桥的最大位移，前5组样本抽样结果及仿真结果如表2所示。

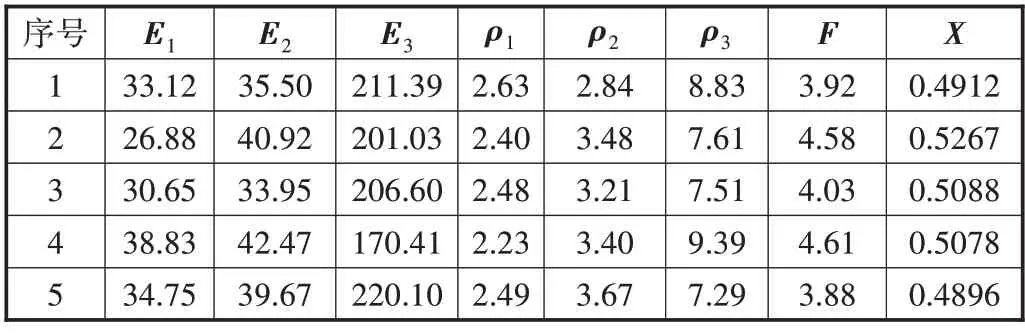
表2 抽样结果及仿真结果分析表

运用GWO-SVR对惩罚因子C和核函数参数g进行优化，根据最小均方差原则选择参数的最佳结果，可以得出C=3.0110，g=3.8073。利用样本点中的训练集对回归机进行训练，最终得到测试集的样本真实值与预测值的对比如图3所示。

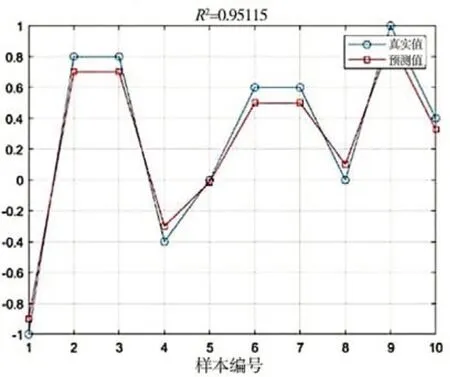
图3 GWO-SVR测试集的预测值与实际值对比图

改进灰狼优化的最小均方误差为：0.0030367，其适应度曲线见图4，在第33代时已得到拟合最优值，可见拟合速度较快，精度较高。

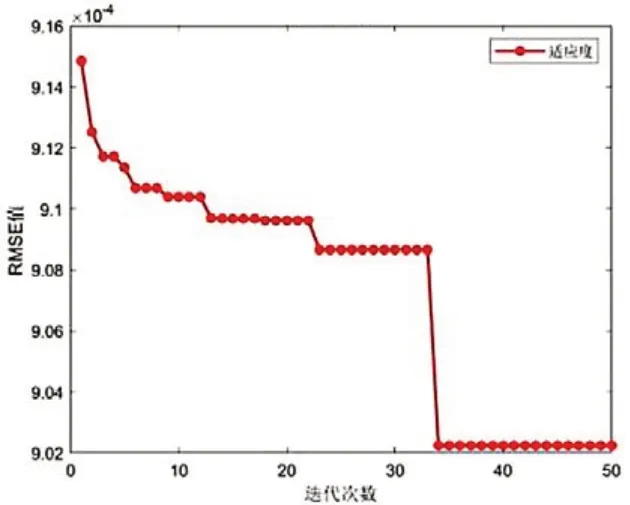
图4 适应度曲线图

6 可靠度指标计算

利用支持向量回归完成结构的功能函数拟合后，根据结构可靠度指标的几何含义，引入惩罚因子C，构造可靠度指标函数方程为：

上式最小值即为结构的可靠度指标，运用粒子群算法迭代求解，求出β的最小值为2.9235。

7 结束语

本文利用SVR代替结构工程可靠度计算中可能出现的复杂隐式功能函数，为了取得更好的拟合效果，采用GWO对SVR中的惩罚因子C和核函数参数g进行优化。使用ANSYS软件进行斜拉桥有限元建模，运用LHS抽样抽取自变量样本点，同时进行风荷载的模拟仿真，将风荷载数据加载到ANSYS斜拉桥模型上以生成样本训练支持向量回归机。在GWO的优化下，SVR模型拟合精度较为理想，对斜拉桥结构的极限状态做出了较好的表达。该方法对于维度较高、非线性程度较大的函数，具有较为理想的拟合精度和收敛速度。并且算法较稳定，鲁棒性较好，可以将GWO-SVR广泛应用于工程结构的可靠度指标计算中。