强轴向加载下翼缘及腹板壁厚比对箱型柱剪力滞效应的影响研究

2023-12-25吴金梁

四川水泥 2023年12期

吴金梁刘凡

(苏州科技大学土木工程学院，江苏苏州 215000)

0 引言

混凝土箱形截面柱本身为内部空心构造，柱身在受力时翼缘板必然会发生剪应力分布不均匀的情况，这就是所谓的剪力滞现象。如果依然按照平截面假定来计算翼缘板内产生的应力，则腹板和翼缘交接处的挠度和应力会与实际情况相差甚远，进而在实际工程中造成严重的问题。为研究强轴方向的剪力滞效应，特引入剪力滞系数λ这一参数，业内人士将剪力滞系数定义为：为考虑剪力滞效应求得的正应力为弯曲平均应力，当λ＜1时为负剪力滞状态；λ＞1时为正剪力滞状态。关于的计算可通过对实际应力曲线图面积，再除以截面翼板宽度进而求得平均应力的近似值。本文对3个不同壁厚比的钢筋混凝土箱型柱进行拟静力试验研究，探究在强轴向加载下翼缘及腹板壁厚比对箱型柱剪力滞效应的影响。

1 试验前期工作

1.1 试件设计

本文为探究腹板及翼缘壁厚比对强轴向剪力滞效应的影响，设计了3个不同壁厚比的钢筋混凝土箱型柱，尺寸参数见表1所示。

表1 试件尺寸参数表

HC-1 为标准模型柱，其尺寸配筋图如图1 所示。HC-2模型柱将腹板壁厚比从标准柱的0.35变为0.5，HC-3模型柱则将翼缘壁厚比从标准柱的0.21变为0.31，尺寸配筋图分别如图2、图3所示。

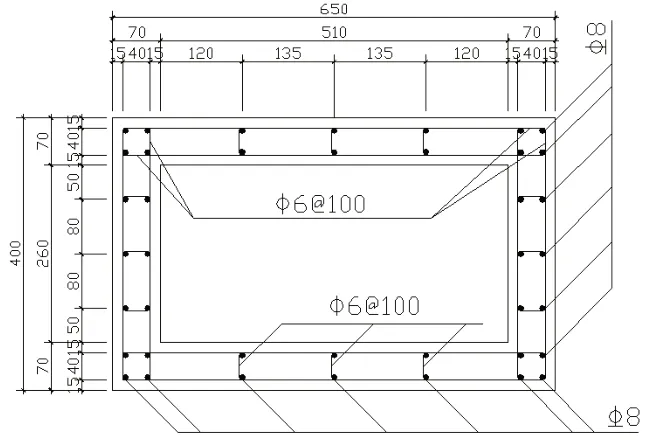
图1 HC-1尺寸配筋图

图2 HC-2尺寸配筋图

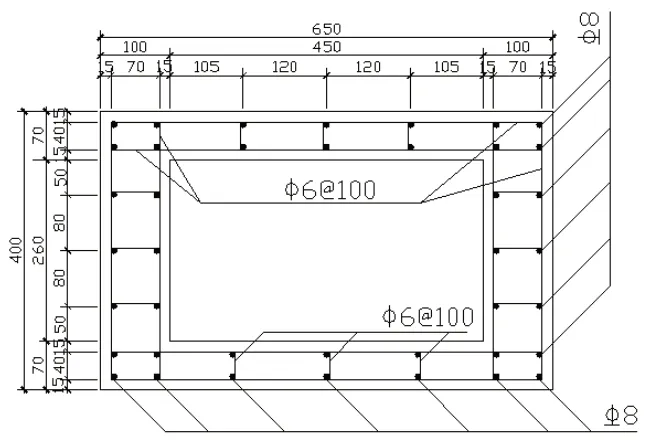
图3 HC-3尺寸配筋图

1.2 加载制度及测点布置

试验按0.1的轴压比对3个混凝土箱型柱施加竖直方向的荷载，再在距试件固端600mm处沿强轴方向施加水平荷载，采取先力后位移加载制度。正式加载前进行预加载，施加10kN往复一次，预加载完毕后，按每30s为一级，逐级增加20kN进行加载，直到箱型柱构件达到屈服；在箱型柱进入屈服阶段后采用位移加载，每一级位移取屈服位移的0.2倍，直至试件加载破坏，加载装置如图4所示，加载制度如图5所示。该试验在箱型柱的固端及距离固端600mm处布置测点，测点布置如图6、图7所示。

图4 HC-2加载装置

图5 加载制度

图6 固端测点布置图

图7 距固端600mm处测点布置图

2 试验结果分析

2.1 腹板壁厚比对强轴向剪力滞效应的影响

图8 为腹板壁厚比分别为0.35 和0.5 的两个试件HC-1和HC-2在固端处的剪力滞系数分布规律曲线对比图。

图8 HC-1与HC-2固端剪力滞系数图

由图8，试件处于混凝土开裂前时，在试件固端受拉区，HC-2翼缘边缘处的剪力滞效应比HC-1严重，随着逐渐向翼缘中部靠近，剪力滞效应由正剪力滞转为负剪力滞，到达翼缘中部又转为正剪力滞，二者翼缘中部剪力滞效应相近，HC-2最大剪力滞系数较HC-1提升了18.2%，如图8（a）所示；在试件受压区，HC-2的最大正剪力滞系数较HC-1下降了2.5%，如图8（b）所示。

试件处于带裂缝工作阶段时，在试件受拉区，HC-2在翼缘边缘处为最大正剪力滞，剪力滞效应比HC-1严重，但随着逐渐靠近翼缘中部，HC-1正剪力滞越来越严重，HC-2 最大正剪力滞系数较HC-1 提升了18.6%，如图8（c）所示；在试件受压区，HC-2的翼缘边缘处的剪力滞效应弱于HC-1，中部剪力滞效应相近，HC-2最大剪力滞系数较HC-1降低了38.6%，如图8（d）所示。HC-1翼缘边缘为正剪力滞效应，中部为负剪力滞效应，但随着腹板壁厚比的提高，HC-2试件屈服进入塑性阶段后，在截面受拉区，HC-2最大正剪力滞系数较HC-1提升了10%，如图8（e）所示；在截面受压区，HC-1和HC-2最大正剪力滞都发生在翼缘边缘，HC-2最大剪力滞系数比HC-1下降了9.7%，如图8（f）所示。

图9 为腹板壁厚比分别为0.35 和0.5 的两个试件HC-1和HC-2在距离固端600mm处的剪力滞系数分布规律曲线对比图。

图9 HC-1与HC-2距固端600mm处剪力滞系数图

从图9中可以看出，在距离固端600mm处开裂前受拉区，HC-1和HC-2的剪力滞效应从翼缘边缘向中部逐渐呈现出由正变负，后由负变正的规律，HC-2最大正剪力滞系数比HC-1下降了30%，如图9（a）所示；在截面受压区，HC-1从边缘向中部逐渐呈现出由负变正，后由正变负的规律，HC-2 最大正剪力滞系数比HC-1 提升了10.4%，如图9（b）所示。

在试件开裂后进入弹塑性阶段时，在柱身纵向中部位置截面受拉区，HC-1和HC-2剪力滞系数曲线都呈现出由负正变负，后由负变正的规律，HC-2的最大正剪力滞系数比HC-1降低了13.7%，如图9（c）所示；在截面受压区，HC-1呈现出翼缘两边为正剪力滞，翼缘中部为负剪力滞的剪力滞效应分布规律，HC-2翼缘中部为2正剪力滞，HC-2 最大正剪力滞系数较HC-1 提升了34.5%，如图9（d）所示。

试件屈服进入塑性阶段后，在柱身纵向中部位置截面受拉区，HC-1和HC-2的剪力滞效应都呈现出由正变负，后由负变正的规律，HC-2的最大剪力滞系数较HC-1下降了16.2%，如图9（e）所示；在截面受压区，HC-1剪力滞系数曲线呈现出由负变正，后由正变负的规律，HC-2则相反，HC-2最大正剪力滞系数较HC-1提升了38.5%，如图9（f）所示。

综上所述，HC-2在固端截面受拉区，在受力的3个阶段，翼缘边缘及翼缘中部的剪力滞效应都要强于HC-1；在截面受压区，3 个阶段的剪力滞效应都弱于HC-1。HC-2在L/4截面受拉区，在受力的3个阶段，翼缘边缘的剪力滞效应都要强于HC-1；在截面受压区，剪力滞系数变化规律不明显，整体上在弹性阶段强于HC-1，在非弹性阶段弱于HC-1。HC-2在L/2截面受拉区，在受力的3个阶段，翼缘剪力滞系数弱于HC-1；在受压区，塑性阶段的剪力滞效应较HC-1出现相反的情况。

2.2 翼缘壁厚比对强轴向剪力滞效应的影响

图10示为翼缘壁厚比分别为0.21和0.31的两个试件HC-1和HC-3在固端处的剪力滞系数分布规律曲线对比图。

图10 HC-1与HC-3固端处剪力滞系数图

从图10中可以看出，试件处于混凝土开裂前时，在固端截面受拉区，HC-1和HC-3剪力滞系数曲线都呈现出由正变负，后由负变正的规律，HC-3最大正剪力滞出现在翼缘边缘，最大正剪力滞系数较HC-1提升了31.3%，如图10（a）所示；在截面受压区，HC-1呈现出由正变负的剪力滞分布规律，HC-3的最大正剪力滞系数较HC-1下降了10.5%，如图10（b）所示。

在试件开裂后进入弹塑性阶段时，在固端截面受拉区，HC-3翼缘呈现出由正变负的剪力滞分布规律，最大正剪力滞系数较HC-1提升了9.3%，如图10（c）所示；在截面受压区，HC-3 翼缘呈现出由负变正的剪力滞分布规律，最大剪力滞出现在翼缘中部，最大剪力滞系数较HC-1下降了50%，整体上HC-3的剪力滞效应弱于HC-1，如图10（d）所示。

试件屈服进入塑性阶段后，在固端截面受拉区，HC-3翼缘剪力滞呈现出由正变负的规律，整体上HC-3的剪力滞效应比HC-1严重，最大正剪力滞系数较HC-1提升了4.5%，如图10（e）所示；在截面受压区，HC-1翼缘剪力滞呈现出由正变负的规律，HC-3呈现出由正变负，后由负变正的规律，最大正剪力滞系数较HC-1下降了11.6%，如图10（f）所示。

图11为翼缘壁厚比分别为0.21和0.31的两个试件HC-1和HC-3在距离固端600mm处的剪力滞系数分布规律曲线对比图。

从图11中可以看出，试件处于混凝土开裂前时，在距离固端600mm处截面受拉区，HC-3翼缘呈现出由正变负的规律，最大正剪力滞系数较HC-1 上升了18.72%，如图11（a）所示；在截面受压区，HC-3翼缘剪力滞呈现出由负变正的规律，最大正剪力滞系数较HC-1提升了40.6%，如图11（b）所示。

在试件开裂后进入弹塑性阶段时，在固端截面受拉区，HC-3翼缘边缘和HC-1都呈现正剪力滞效应，逐渐靠近翼缘中部的过程中，HC-1由正变负，后由负变正，HC-3中部为负剪力滞，最大正剪力滞系数较HC-1 下降了12.7%，如图11（c）所示；在截面受压区，HC-1翼缘剪力滞由正变负，HC-3翼缘剪力滞由正变负，后由负变正，最大正剪力滞系数较HC-1下降了6.9%，如图11（d）所示。

试件屈服进入塑性阶段后，HC-1翼缘边缘负剪力滞越来越严重，翼缘中部为正剪力滞，而HC-3在翼缘中部为负剪力滞，最大正剪力滞出现在翼缘边缘，最大正剪力滞系数较HC-1 下降了18.3%，整体上剪力滞效应弱于HC-1，如图11（e）所示；在截面受压区，HC-3翼缘剪力滞由正变负，后由负变正，与HC-1呈相反规律，最大正剪力滞系数较HC-1提升了11.9%。如图11（f）所示。

综上所述，HC-3在固端截面受拉区，在受力的3个阶段，受拉区翼缘整体上剪力滞效应都要强于HC-1，在受压区则都弱于HC-1。HC-3在L/4截面受拉区，在弹性阶段，翼缘边缘的剪力滞效应较HC-1出现了相反的情况；在截面受压区，剪力滞系数曲线出现无规律的分布情况，整体上弹塑性阶段的剪力滞效应稍弱于HC-1。HC-3在L/2截面处剪力滞系数曲线较HC-1变化规律不明显。