网格尺寸对识别循环流化床上升管中颗粒聚团特性的影响研究
2023-12-22夏云飞陈逸伦
夏云飞,陈逸伦
(中国电建集团装备研究院有限公司,上海 201316)
循环流化床(CFB)上升管中最典型的流体动力学行为是存在颗粒聚团。许多研究者已经对聚团进行了大量实验研究并得到了较有价值的定性特征[1-3]。为了定量地考察聚团特性,需要建立聚团识别准则。Liu等[4]提出采用局部颗粒浓度信号作为评估聚团形成程度的量化指标。Lints和Glicksman[5]提出根据颗粒浓度的阈值定义聚团。Soong等[6]提出的三个聚团识别准则最全面且被广泛接受。在该基础上,Tuzla等[7]提出了一个2σ准则,即聚团的局部瞬时颗粒浓度必须大于时间平均颗粒浓度至少两倍的标准偏差(2σ),并使用该准则研究了快速流化床中聚团的特性。Sharma等[8]基于Tuzla等的工作提出了一种改进的准则,他们认为若通过2σ准则检测到聚团,则聚团存在于瞬时颗粒浓度大于平均颗粒浓度的时间段内,并使用该准则研究了颗粒粒度和流化速度对聚团特性的影响,该准则已被研究者广泛用于实验研究。Manyele等[9]采用该准则研究了高通量和高密度上升管中的聚团特性。Liu等[10]基于PDPA的测量结果研究了CFB上升管中稀相气固流中的聚团特性,聚团识别准则最初是为了研究实验中的聚团特性而提出的,近期才被用于数值模拟中。基于Sharma等提出的准则,Cabezas-Gómez等[11]利用MICEFLOW代码研究了CFB上升管中的聚团特性。Helland等[12]研究了快速CFB中气流速度对聚团特性的影响。Wang等[13]采用一种随机方法研究了CFB上升管内稠密气固流中的聚团特性。上述研究表明:尽管模拟结果和实验结果具有相同的数量级,但仍存在显著差异,这可能是实验和模拟研究中用于聚团识别的采样体积不同所导致的。
采用LES-DSMC 方法对CFB 上升管中的气固两相流动特性进行了数值模拟,采用不同尺寸的网格进行聚团识别,分别考察了网格尺寸对中心区域和近壁区域聚团特性的影响规律,得到了数值模拟中聚团识别的相关经验和结论,并提出了近壁区域中聚团平均颗粒浓度和下降速度的计算方法。
1 欧拉-拉格朗日气固流动模型
1.1 气相
气相质量和动量守恒方程[14]如下。
式中:ug和ρg为气相速度和密度,εg为空隙率,Sp-g是两相之间的曳力,μlam,g和μt为气相层流和湍流的黏度。
气相湍流黏度的计算公式如下[15]。
式中:Δ=(ΔxΔy)1/2,为气体湍动能量。
1.2 颗粒运动
颗粒运动服从牛顿运动方程[16],公式如下。
式中:m为颗粒质量,vi为颗粒速度,fd,i为颗粒所受曳力,Cd0,i为曳力系数。
1.3 颗粒碰撞
颗粒碰撞过程采用DSMC 方法处理,碰撞对由碰撞概率理论决定而不是根据颗粒轨迹得出,模拟中颗粒i 和j 的碰撞概率Pij为:
式中:n为局部颗粒数密度;d为粒径;uij为颗粒i和j之间的相对速度,Δt为时间步长,g0为径向分布函数,颗粒最大堆积体积分数εmaxs为0.63。
两个颗粒碰撞后的速度变化遵循以下等式:
式中:vi,0和vj,0为碰撞前颗粒i和j速度,vi,1和vj,1为碰撞后颗粒速度。
2 初始和边界条件
模拟的二维上升管截面见图1。

图1 模拟网格布置
由图1 可见:上升管被划分为2200 个计算网格,网格尺寸为0.45 cm×0.9 cm,将每个计算网格再被划分为9 个尺寸相同的子网格。模拟中,在计算网格中计算气相和固相之间的相互作用,在子网格中研究颗粒碰撞。
上升管中气流和颗粒初始速度设置为零,给定了入口气相压力、气流速度和颗粒速度,假设底部入口各边界条件均匀,气相采用无滑移壁面条件。模拟参数见表1。
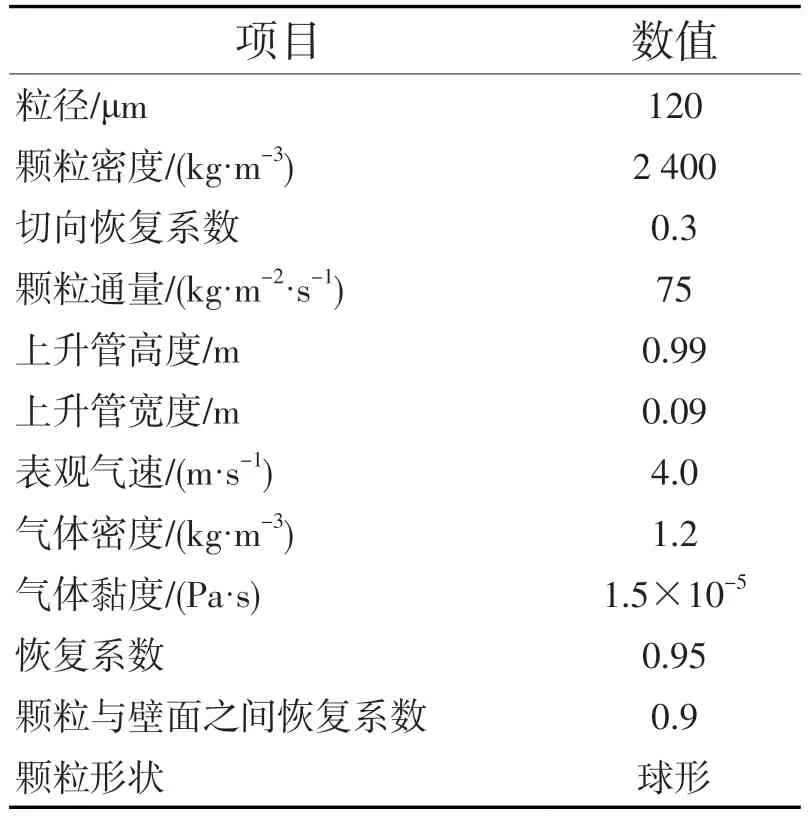
表1 模拟参数

表2 模拟中使用的聚团识别网格
3 聚团识别方法
为了获得CFB 上升管中聚团定量特性,Soong等[6]首先提出了识别聚团的3 个必要条件:①在指定的局部位置,聚团的颗粒浓度必须显著高于时均颗粒浓度;②由聚团引起的颗粒浓度变动必须大于颗粒浓度的随机波动背景值;③对于测量颗粒浓度变动的取样体积,其特征长度需大于颗粒直径1~2 个数量级。基于以上条件,Tuzla 等[7]提出了一个2σ准则,即聚团的局部瞬时固体浓度必须大于时均颗粒浓度至少2 倍的标准偏差,当瞬时颗粒浓度超过该阈值时聚团形成,再次降至该阈值以下时聚团消失。Sharma等[8]又提出了一个修正准则:聚团的形成时间是其颗粒浓度在满足2σ准则之前最后一次超过时均颗粒浓度的时间,而聚团的消失时间是其颗粒浓度不符合2σ准则后第一次降至εs以下的时间,该聚团识别准则已被广泛认可及应用。
基于此准则,可得到以下聚团特性。
1)聚团平均持续时间τ'c:
式中:n为一个观察期T中检测到的聚团总数。
2)聚团出现频率λc:在采样空间内观察到聚团的频率。
3)聚团的存在时间分数Fc:
4)聚团平均颗粒浓度ε'c:
式中:εi为已识别聚团i的颗粒浓度。
5)聚团平均轴向速度v'c:
式中:vi为已识别聚团i的轴向速度。
笔者共采用9 种尺寸的网格进行聚团识别,每种网格的宽高比约为0.5(Δxi/Δyi≈0.5)。因此,网格尺寸可以由网格面积S(S=Δxi×Δyi)表示。
4 结果与讨论
4.1 网格尺寸对聚团识别的影响

图2 床层平均聚团特性随采样面积的变化
综上分析,减小网格面积S 是提高模拟中聚团识别精度最直接和有效的方法,但气固两相模拟中,通常需要的计算网格足够大,以具有代表性的体积更便于准确估计孔隙率[12]。另外,随着S 的减小将导致计算时间显著增加,因此在模拟中S 通常大于0.1 cm2,如Cabezas-Gómez 等[11]采用了最小的0.58 cm2,Helland 等[12]采用了0.125 cm2。为了解决以上问题,笔者采用独立于气相网格的聚团识别网格,由于聚团识别网格是独立的,可称其为“数值探针”,只在重点关注的位置放置识别网格,通过这种方式,可在不影响计算网格和不增加计算负荷的情况下大幅提高聚团识别的准确性。CFB 上升管中心区域和近壁区域的聚团表现出较不同的流动行为。
4.2 聚团的径向分布特性
在无量纲高度y/H=0.5 处,聚团平均颗粒浓度ε'c的径向分布及与Sharma 等实验数据的对比情况见图3。

图3 聚团数均颗粒浓度的径向分布
由图3 可见:近壁区域(|x/R|>0.9)聚团颗粒浓度较高,而中心区域的ε'c(|x/R|<0.9)较低且随床层径向位置变化不大。当S 为0.045 cm2时ε'c与实验数据基本一致,S增加会在一定程度上改变定量结果,但不会改变ε'c的径向分布特性。
无量纲高度y/H=0.5 处,聚团平均持续时间τ'c的径向分布及与Sharma等实验数据的对比情况见图4。

图4 聚团平均持续时间的径向分布
由图4 可见:不同面积S 条件下,τ'c径向分布相似,τ'c随着S 的增加而增加,并且从中心到壁面,增幅越来越大。当S 为0.045 cm2时,τ'c的分布与实验数据较吻合。此外,在近壁区域,τ'c随与壁面径向距离的变化而变化,径向距离较小时,τ'c较大。Rhodes等[18]通过高分辨率摄像机发现了贴壁区域相对较慢的聚团,但Sharma等[8]在实验中未发现相关聚团,原因可能是实验中探头的空间分辨率低,因此,数值模拟可以作为高精度聚团识别的补充工具。
4.3 壁面下降流中的聚团特性
3 种网格尺寸对壁面区域颗粒聚团识别结果的差异见图5。其中,16 s 时上升管局部区域的典型快照见图5(a),壁面区域高度29.7~30.6 cm 单元中聚团局部放大图见图5(b)~(d)。
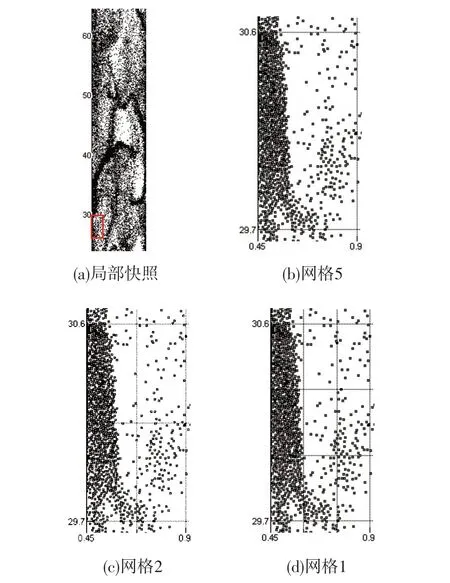
图5 3种网格尺寸对壁面下降流中聚团的识别
由图5(b)可见:当S 为0.405 cm2时,网格宽度正好等于模拟中的壁面下降流厚度(δfilm=Δx5=0.405 cm),壁面下降流中出现的所有聚团均可包含在贴壁网格中,但该网格中存在显著的颗粒浓度差异。
CFB 上升管壁面区域的颗粒流通常被认为是一系列聚团组成的下降流。Harris 等[20]根据大量实验数据建立了预测壁面下降流中平均聚团颗粒浓度和下降速度的关系式:
与图5 相对应的3 种识别网格(网格5、网格2、网格1)下模拟得到的聚团壁面下降流中平均聚团颗粒浓度见图6。当S=0.405,0.1,0.045 cm2时,随εs的变化情况以及由公式(17)计算的结果见图6(a)~(c)。

图6 平均聚团颗粒浓度随上升管中床层横截面平均颗粒浓度的变化情况
由图6 可见:模拟结果和公式(17)计算的结果之间存在显著差异,从上述可知这种差异是由聚团识别过程中产生的误差引起的。
由图5(b)可见:S=0.405 cm2时,网格中存在显著的颗粒浓度差异,该聚团瞬时二维颗粒浓度(εc)2D取值为此时该单元中的数均值并通过公式(19)计算,公式(19)中的面积S 包括了该单元中稀相区域的面积。与此类似,该聚团的瞬时轴向速度也为该单元中颗粒的数均轴向速度,由公式(20)计算,该单元中稀相区域的离散颗粒的轴向速度也在式(20)中被平均。在聚团识别过程中产生的上述误差将累积并带入和中。由图5(c)可见:若采用S=0.1 cm2网格划分壁面下降流区域进行聚团识别,局部稀相区域可与密相聚团区域区分开来并因颗粒浓度较低而不参与聚团特性计算。由图5(d)可见:若采用较小的S=0.045 cm2对壁面下降流进行网格划分,聚团特性计算时可剔除更多的稀相区域,对比图6(a)~(c)可见:网格尺寸越大,识别出的平均聚团颗粒浓度与理论计算结果的偏差越大,当S=0.045 cm2时,聚团识别结果与式(17)计算结果更吻合。

图7 随的变化情况
由图7 可见:当S=0.405 cm2时,明显偏离实验数据。当采用网格1 和网格2 进行聚团识别且由式(22)计算时,与相应实验数据接近。与相似,随着单元尺寸的减小,更接近实验数据。
上述结果表明,模拟中应对壁面下降流层进行精细的识别网格划分以提高聚团识别精度,进而提高和的计算精度,因此笔者提出采用公式(21)和(22)来计算模拟中的和。
式中:Nr是壁面下降流厚度上径向网格数(Nr=2δfilm/Δxi),nj是单元j中识别出的聚团数,εc,i和vc,i是聚团i的三维颗粒浓度和下降速度。
5 结论
基于聚团识别准则在模拟中的应用,考察了网格尺寸(网格面积)对聚团特性预测的影响,并得到了模拟中聚团识别的相关结论。
1)提出了壁面下降流中聚团平均颗粒浓度和下降速度的预估方法。结果表明,减小网格尺寸是提高上升管中聚团识别精度和获得上升管中聚团特性详细分布的有效方法,独立的聚团识别网格可显著减小模拟中的网格面积、消除计算网格的维数限制,同时提出了“数值探针”技术。
2)对于中心区域的聚团,增大网格尺寸将在一定程度上改变定量结果,但不会改变聚团特性的分布情况,该变化主要是由于中心区域聚团尺寸呈多尺度分布。床层平均聚团特性随网格尺寸大致呈线性变化。对于近壁区域的聚团,随着网格尺寸的增加,得到的数据点减少,平均聚团特性与实际值的偏差越来越大,该偏差主要是由于近壁区域聚团特性沿径向变化较大。
3)提出的壁面下降流中聚团平均颗粒浓度和下降速度的预估方法可有效提高预测精度,有助于将聚团识别准则较好地应用于模拟分析中。
