羊毛纤维平均直径检测结果差异性分析
2023-12-21董绍伟
徐 静,董绍伟
(1.扬州工业职业技术学院 基础科学部,江苏 扬州 225127; 2.南京海关工业产品检测中心,江苏 南京 210019)
细度是羊毛纤维的一项重要指标,关系到羊毛的强度、伸长率、卷曲、弹性、弯曲刚度、吸湿性等多项性能以及成纱质量,是羊毛分级定价的主要依据和羊毛贸易中的重要指标。由于羊毛纤维的横截面近似圆形,因此可以使用平均直径表示细度。
目前,国内外成熟的测试羊毛纤维平均直径的方法主要有投影显微镜法、光学纤维直径分析仪(OFDA)法、激光扫描法、气流仪法等。其中,投影显微镜法、OFDA法、激光扫描法是直接对纤维的轮廓进行测量,以轮廓宽度代表纤维直径的直接测量方法;气流仪法是通过测试气体的流量来间接测定纤维直径的间接测量方法。从纺织行业与检测机构的发展来看,快速、高效、准确、操作简单的测试方法更受欢迎,因此相对于受检测人员主观因素影响且检测效率较为低下的投影显微镜法,OFDA法、激光扫描法和气流仪法推广应用更为广泛。
张烨[1]运用方差检验对投影显微镜法和电子显微镜法检测结果进行了评价,结果表明2种仪器检测结果没有显著性差异;孙宝芬等[2]以标准毛条标准值对气流仪法和激光扫描法的差异性进行了对比分析,表明2种检测方法结果存在差异;姚苗苗等[3-4]运用t检验研究得出激光扫描法、OFDA法、投影显微镜法检测羊毛毛条和分梳山羊绒的结果存在显著差异。但上述研究在做显著性分析之前,均未对统计数据进行正态性和方差齐性检验,也未分区间比较区间内部差异。
本文分别采用OFDA法、气流仪法和激光扫描法3种方法测试不同直径的羊毛条,对测试结果采用MatLab和SPSS软件中的参数和非参数检验进行总体和区间的差异性分析,判断在日常检测中采用不同的测试方法得到的羊毛纤维平均直径测试结果是否存在差异,探究3种方法的差异性及其相互矫正的方法。
1 试验材料
1.1 羊毛条样品
为减小样品不均匀性给测试结果带来的偏差,选用的羊毛条样品为2017—2022年6个年度12期国际羊毛实验室(INTERWOOLLABS)毛条比对样品,共96个。
1.2 试验仪器
OFDA-4000光学纤维直径分析仪(澳大利亚IWG集团);羊毛纤维细度仪(使用2台做平行样,新西兰羊毛检验公司);Sirolan Laserscan激光细度仪(澳大利亚羊毛检验局);GL224i-1SCN电子天平(精度为0.01 mg,德国赛多利斯集团);双刀切断器(切取长度1.8~2.0mm,澳大利亚羊毛局)。
2 试验方法
2.1 执行标准
OFDA法执行标准IWTO—47∶2013《使用光学纤维直径分析仪测定羊毛纤维平均直径及分布的方法》;气流仪法执行标准IWTO—6∶2013《使用气流仪测定精梳毛条中纤维平均直径的试验方法》;激光扫描法执行标准IWTO—12∶2012《使用塞洛兰-激光扫描纤维直径分析仪测定纤维平均直径和直径分布》。
2.2 试验温湿度环境
试验采用标准大气条件,温度为(20±2)℃,相对湿度为(65±3)%。
2.3 制样及预处理
将试验样品根据OFDA、气流仪、激光细度仪要求和标准规定分别制备试样,每个样品制备8个试样,放置于标准大气中调湿。试样调湿平衡后进行后续测试。
2.4 测试步骤
利用INTERWOOLLABS提供的标准毛条对OFDA、气流仪和激光细度仪进行校准,使其处于良好的工作状态,确保试验结果准确。按照2.1节中的标准方法开展测试。
3 结果与讨论
3.1 测试结果
分别使用OFDA法、气流仪法和激光扫描法3种方法对每个样品的8个试样测试后,取其平均值,3种方法平均直径测试结果如表1所示。

表1 3种方法平均直径测试结果Tab.1 Average diameter test results of three methods
3.2 3种测试方法平均直径总体差异性分析
3.2.1 正态分布检验
在数据应用中,假定计量数据的参数不可知性,首先进行的是数据的正态性检验和方差齐性检验[5-6]。
将OFDA法、气流仪法、激光扫描法的测试数据集分别记为X、Y、Z。将这3组数据分别带入MatLab中,使用[h,p,L,C]=lillietest()命令判断数据是否具有正态分布的性质,其中h为检验结果,若h=0,则接受向量是服从正态分布的假设,若h=1,则可以否定向量服从正态分布;p为接受正态分布假设的概率,p很小说明符合正态分布的概率很小;L为测试统计量;C为是否拒绝原假设的临界值,若L>C,则拒绝正态分布假设。在显著性水平为0.05的条件下,正态分布检验结果如表2所示。

表2 正态分布检验结果Tab.2 Test results of normal distribution
X、Y、Z的h=1,表示拒绝正态分布的假设,X、Y、Z均不服从正态分布。从正态分布检验结果来看,3种测试方法总体结果均不能通过正态性检验,不满足参数检验条件,因此采用非参数检验法对测试数据的总体分布形态进行检验。
3.2.2 Mann-Whitney U检验
2个样本的Mann-Whitney U检验[7]是一种非参数统计方法,以中位数为测度,观察2组数据样本的分布是否具有显著性差异。
设A、B为2个独立的样本,来自2个分布F(x)和F(x-μ),按式(1)~(3)计算U值统计量。
(1)
(2)
U=min(U1,U2)
(3)

当A、B的容量和N≥50时,U近似正态分布,将U按式(4)进行Z变换转换成标准正态分布。
(4)
运用SPSS 26.0软件分别对OFDA法和气流仪法、OFDA法和激光扫描法、气流仪法和激光扫描法检测数据进行Mann-Whitney U检验。建立检测数据具体假设:
H0:2种仪器检测数据具有相同的分布。
H1:2种仪器检测数据具有不相同的分布。
Mann-Whitney U检验结果如表3所示。

表3 Mann-Whitney U 检验结果Tab.3 Mann-Whitney U test results
经过Mann-Whitney U检验法分析,OFDA法和气流仪法p=2P(Z≤-0.23)=0.818>0.05(P为单边概率),OFDA法和激光扫描法p=0.938>0.05,气流仪法和激光扫描法p=0.895>0.05,拒绝H1,接受H0,因此3种检测方法总体不存在显著性差异。
3.3 3种测试方法平均直径区间差异性分析
将测试数据按从小到大排序(编号1~96)得到散点图见图1。3种测试方法总体结果没有显著性差异,但从按大小排序后的测试结果可以看到在部分直径区间范围内,数据可能存在微小差异。所以需要将直径区间进行合理划分,进一步研究测量数据在不同直径区间的差异性。

图1 数据按从小到大排序后的散点图Fig.1 Scatter plot of data sorted from smallest to largest
3.3.1 数据直径区间分组
首先将12期、每期8个数据按从小到大的数值均分,共分8组、每组12个数据,直径数据均匀分组如表4所示。

表4 直径数据均匀分组Tab.4 Uniform grouping of diameter data
采用K-Means聚类[8-9]方法重新分组。聚类分析是一种非监督的学习算法,根据组内样本最小化而组间距离最大化的原则将数据划分为若干组。目标函数为误差平方和SSE:
(5)
(6)
式中:Ei为第i个聚类组;ei为第i个聚类组的中心点;y为Ei的样本点;d(ei,y)为ei和y的欧氏距离;ni为Ei的样本个数。
和均分一样,设定聚类个数k为8,最大迭代次数为500次,距离函数为欧式距离,运用Python编程[10]得到直径聚类分组如表5所示。聚类后的样品分组直观图如图2所示。从图2中可以看出数据聚类效果较好,基本实现组内差距小、组间差距大的目标。

图2 聚类分组直观图Fig.2 Visual diagram of clustering grouping

表5 直径聚类分组Tab.5 Diameter clustering grouping
3.3.2 3种测试方法在不同直径区间结果的差异性分析
首先对8组数据分别进行正态和方差检验。正态检验使用MatLab中的lillietest()函数,置信区间95%,p值结果如表6所示。

表6 分组数据正态检验Tab.6 Normal test for grouped data
由于大部分数据服从正态分布,进一步对数据进行方差齐性检验。方差齐性检验使用SPSS 26.0中的Levene检验,分组数据方差检验如表7所示。除了第15组,其余组数据的p值均大于0.05,满足方差齐性要求。

表7 分组数据方差检验Tab.7 Test of variance for grouped data
从正态检验和方差齐性检验的结果来看,第9、13、14组数据既符合正态分布也符合方差齐性检验,所以这3组数据可用参数检验,其他组数据两两比较时,如果2组均正态和方差齐性,则选择参数检验,否则,选择非参数检验。参数检验选择成对样本t检验,非参数检测选择双独立样本的Mann-Whitney U检验,在置信区间95%的条件下进行假设检验,假设检验结果如表8所示。若气流仪法检测结果落在聚类中心为15.91(第9组)聚类组中,则与OFDA法、激光扫描法有显著差异;第10组、第11组、第12组、第15组3种测试方法均无显著差异;OFDA法检测结果落在聚类中心为26.78(第13组)或30.33(第14组)的聚类组中与气流仪法、激光扫描法有显著差异;激光扫描法检测结果落在聚类中心为36.12(第16组)与气流仪法、OFDA法有显著差异,检测结果与图2显示基本一致。
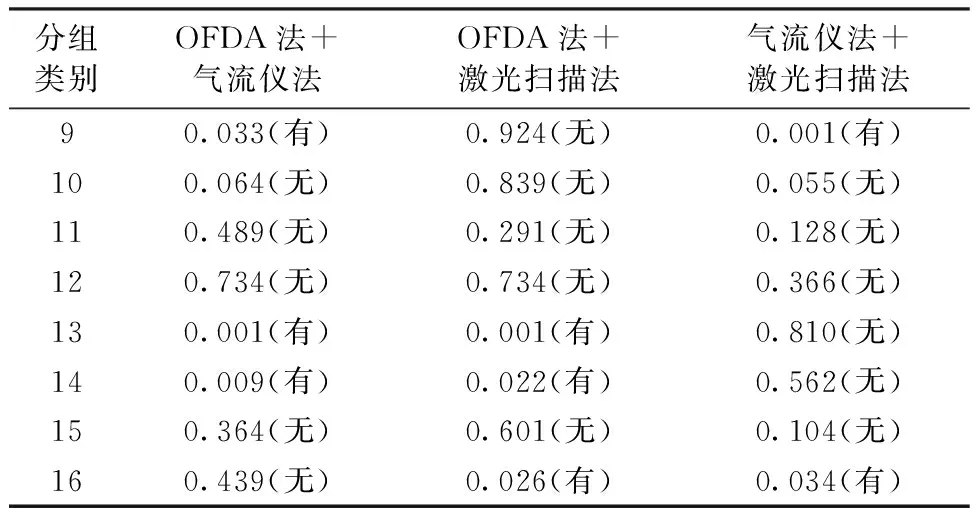
表8 假设检验结果Tab.8 Results of hypothesis testing
3种测试方法存在差异性的原因主要是测试原理不同,OFDA法是将毛条样品切成2.0mm左右长度的小段,均匀散布在载样片上,经透射光学显微镜放大后,扫描采集纤维显微图像,通过图像识别分析技术对直径进行测量;气流仪法是根据流动力学原理,一定质量的羊毛纤维比表面积与其纤维直径成反比,当一股气流通过装有羊毛样品的圆柱体时,气流流量和压力之比取决于纤维的总表面积,间接估计羊毛纤维平均直径;激光扫描法是将毛条样品切成2.0mm左右长度的片段,加入到一定的试剂中分散,然后通过安装在激光束中的测量元件,毛条使激光束的强度减弱,对减弱程度进行感应并转化为平均直径。由于测试原理不同,当样品的平均直径较小或较大时,3种方法测量产生的偏差可能会相对更大。
3.3.3 回归分析
由于第9、13、14、16组测量数据存在显著性差异且数据满足方差齐性,因此可对数据进行回归拟合,以有显著差异的测量方法组为因变量,其他2组测试方法分别为自变量,回归方程如表9所示。第9、13、14、16组数据回归方程的拟合度均较高,说明回归方程预测有效,3种测量方法之间可以相互预测。
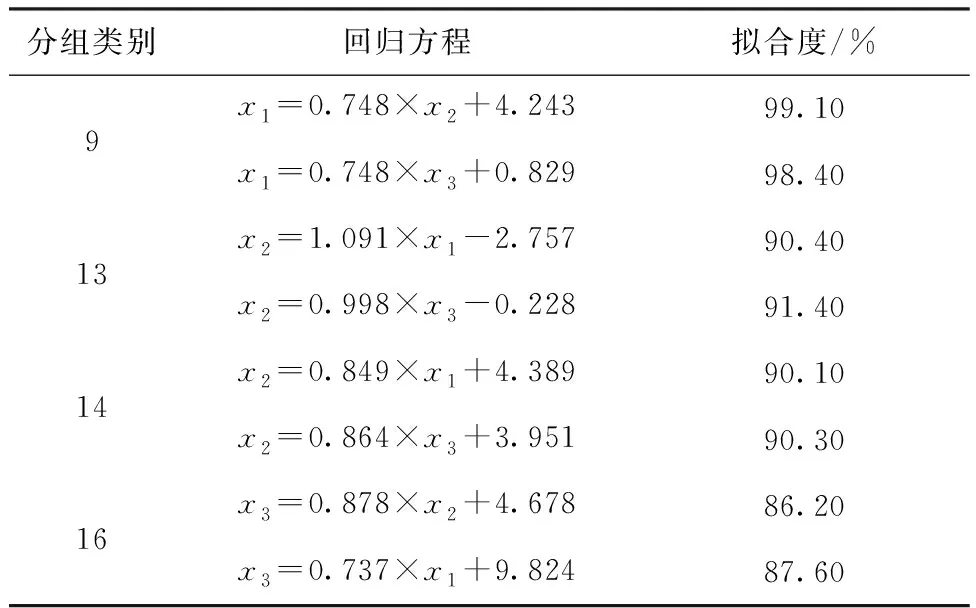
表9 回归方程Tab.9 Regression equations
4 结 论
本文通过Mann-Whitney U秩和检验法对由OFDA法、气流仪法和激光扫描法测量的羊毛纤维平均直径两两整体之间是否存在差异进行了假设检验,研究结果表明OFDA法、气流仪法和激光扫描法3种方法测量总体结果在显著性水平0.05的条件下是无差别的。
按大小排序后的部分直径区间范围内,数据可能存在微小差异,运用K-Means聚类算法将直径区间分8类进行聚类划分,在不同区间研究数据的差异性,结果表明3种检测方法在数据值较小和较大时会有1种方法和其他2种方法存在显著差异。对于有显著差异的组别,回归分析表明有差异的1组可以分别用其他2组的线性关系式表示且拟合度较高,说明当存在显著差异时,3种测量方法之间是可以相互预测的。
