基于SEIR模型的数字化技术在重大疫情应急预案中的应用*

杨利超,赵泽惠,胡梦之,张鹤立,伍丽群,庄诺亚,梁万年,5△,朱纪明,5△

(1.苏州大学苏州医学院公共卫生学院,江苏 苏州 215123;2.北京邮电大学;3.清华大学万科公共卫生与健康学院; 4.深圳市卫生健康发展研究和数据管理中心; 5.清华大学健康中国研究院)

新冠疫情的蔓延唤醒了人们对公共卫生安全的意识。在引发全社会对重大传染病疫情防控应急预案和应急响应机制关注[1]的同时,还创新了数字化技术在疫情预测、防控救治、资源调度、决策评估等方面的应用场景[2-4]。然而,公共卫生应急管理和疫情防控应急预案制定的信息化进展相对滞后,缺乏能够实现应急准备的系统理论和技术支持,限制了传统应急预案的可及性和实用性[5]。因此,在将设计更高效、更科学、更实用的重大疫情应急预案作为国家提升重大疫情应急管理能力建设重点[6]的同时,把数字化技术融入应急预案的制定也将成为重大疫情应急管理能力提升的关键途径。

应急预案起源于1974年英国卫生与安全委员会因弗利克斯巴勒化工厂爆炸事故而提出的应急计划,我国对于应急预案的研究兴起于2003年“非典”事件之后[7]。作为突发公共卫生事件防控中“预防为主”理念的重要体现之一[1],规范的应急预案应具备预见性、应急性、系统性和可操作性四个特点[5]。目前我国的预案制定与应用已形成包括总体预案、专项预案等在内的各层级各类别协调统一、各司其职的卫生应急预案体系,但相关体系在完善过程中仍然存在如预案质量和可操作性需要提升[8]、体系和风险变化衔接不到位[9];地方预案生硬照搬上级预案、预案内容过于简单或繁琐、不同级别预案缺乏有机联系[10]等问题。

针对上述问题,数字化技术应用于应急预案管理系统可以有效支撑并实现传统应急预案的动态管理,通过紧密关联应急预案、应急资源与突发事件信息,实现智能辅助决策支撑,提升预案的及时有效性[10]。其次,数字化技术具有灵活性、动态性等特征,能够根据疫情变化情况动态调整预案内容,提升预案多地区适配的可操作性。最后,以大数据为基础的预测模型,基于数字化技术可以更精确的模拟疫情传播图景,针对疫情在不同地域和严峻程度的差异,实现资源的高效配置。

从整体研究方向来看,国内外学术界对应急预案的研究集中在编制原则与方法、体系与作用逻辑、决策与质量评估等领域[11,12]。Matteo C, Jessica T. D等人应用全球集合种群流行病传播模型预测了2020年1月23日实施的国际旅行和隔离政策对全球疫情传播动态的影响,结果证实相关政策不仅将中国境内的疫情发展推迟了3至5天,相关国际旅行政策还显著减缓了病毒在全球的传播[13], 为出行相关防控政策的实施提供了科学证据。周燕等[14]通过分析一系列聚集性疫情的发生,对今后的疫情防控策略提出了建议。张婷等[15]基于对疾病的现有认识,针对不同情景分别使用传染病传播动力学模型和大流行理论静态模型进行医疗资源需求评估。Savoia E, Testa MA和Biddinger PD[16]通过大量桌面演练和问卷调查,对地方公共卫生机构应对大规模突发事件的应急能力进行了研究。但是,这些研究大部分集中在管理学公共政策层面的回顾性研究,并没有结合实际疫情传播轨迹搭建模型,给出相关政策建议。虽然,少部分也构建了流行病传播模型,但是忽略了与我国应急预案内容相对应,导致提出的政策建议缺乏普适性,无法及时指导多地区的疫情防控策略实施。因此,本文将应急预与流行病传播模型相融合,借助数字化技术动态生成应急预案,提升应急预案的灵活性、及时性、有效性。

为了使应急预案跨越时间、空间的限制,数字技术开始被广泛应用在自然灾害、事故灾难、社会安全等突发公共事件。陈超等[18]利用数字孪生技术和增强现实技术,研究灾害数字孪生体的构建方法,开发了一种新型应急预案演练系统。宁玉辉等[22]将Petri网引入系统建模,并进行了适应性修改,实现了智能化应急预案析出、应急资源调度策略生成等功能。然而,数字技术在公共卫生领域及重大传染病疫情方面的研究和应用有限[23],具备的自动化和智能化的数据挖掘、结果分析、科学调度等相关特点在疫情防控系统中并未得到广泛的应用[24]。

为了创新SEIR模型在疫情发展预测和应急决策中的应用场景,推动数字化技术在应急预案制定中的使用,本研究将改进SEIR模型中涉及的参数来源划分为三类。一是与流行病学特征相关联的参数,取自参考文献和权威资料;二是防控措施干预下的相关参数,抽象提取出多个干预函数;三是防控措施干预下的流行病学特征参数,采用多轮迭代拟合的方式。因此,本模型可根据疫情发展,更新拟合变量,获取相关流行病学特征参数,借助本研究所设计的干预函数即时生成的应急预案,为防控措施的实施提供具有时效性的参考依据。此外,本研究还为改进SEIR模型搭建了MATLAB实验环境,实验生成数字化应急预案,为我国防控政策的调整和医疗资源配置提供快速、有效的决策支持、理论依据和工程基础。

1 资料与方法

1.1 数据来源与假设

本文所采用的真实疫情数据部分来源于国家卫生健康委员会(http://www.nhc.gov.cn/)疫情通报数据,还有部分来自文献、权威资料等公开数据[25-31]。

(2)假设境外输入采取严格的闭环处理,不存在境外阳性患者溢出情况。

(3)假设不存在新冠治愈特效药。

迷走神经刺激可能有远期效果而被批准用于难治性的抑郁症患者。没有资料证实它有快速的效果，因此不能用于抑郁症的急性期治疗。迷走神经刺激可作为其他抗抑郁治疗的辅助措施。

(4)康复者会产生抗体,近期不会再被感染。

1.2 改进SEIR传染病动力学模型

SEIR模型是传染病研究的经典动力学模型,最早由Kermack W等[30]于1927年提出。模型简洁,参数较少,可被广泛地研究和使用。SEIR模型假设在一个复杂网络群体中所有个体可大致分为易感者(Susceptible,S)、暴露者(Exposed,E)、感染者(Infected,I)和康复者(Recovered,R)等若干种群组状态;随后,研究者可根据流行病发展和研究阶段的需要,将状态组合使用以表现不同状态之间的转换顺序和流行病所处的阶段。本文在传统SEIR模型的基础上,结合我国新冠肺炎疫情的防控政策,设置政策性状态群组。研究总结我国目前主要采取的疫情防控政策如下:境外入境人员的闭环管理;全民核酸定期筛查;集中隔离感染者的密接者;居家隔离感染者的次密接者;定点医院救治感染者;鼓励全民接种新冠疫苗等。具体的群组状态转化关系如图1所示,图中黑色箭头表示各个群组状态间的转化关系。

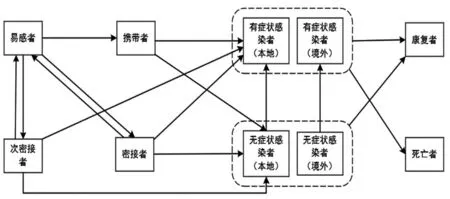
图1 改进SEIR传染病动力学模型

(1)本文引入了与全民核酸定期筛查相关的政策性状态群组携带者C。由于奥密克戎变异株在潜伏期内具有高传染性,传统的SEIR模型不再适用于由奥密克戎变异株引起的传播。于是,本研究引入携带者C代替了传统SEIR模型中暴露者E,并将该群组定义为已经携带奥密克戎病毒,但在被确诊为阳性前,一直隐匿在本地疫情传播链条中。

(3)2022年6月28日发布的《新型冠状病毒肺炎诊疗方案(试行第九版)》指出,我国对于密接者采取7日集中隔离和7日居家健康监测和次密接者采取7日居家健康监测政策。于是,本模型中新增群组密接者(Cc)和次密接者(Sa)。

改进SEIR动力学方程构建如下:

1.3 模型参数赋值和拟合检验

本文主要采用如下三种方式设置改进模型的相关参数R0、Rt、ρ、νc。第一种是新型冠状病毒流行病学特征可量化的固有参数,可从相关参考文献或搜集的数据资料中获得(如表1所示)。第二种是防控政策干预下的干预参数σ、ps、pc、χ、Γ、Δ、 Φ、Ω,可根据当时的防控政策设置干预函数(如表2所示)。第三种是防控政策干预下的流行病学特征参数w、τ、ε、∈,可通过最小二乘法估计获得(如表3所示),下文将给出详细说明。

表1 改进SEIR动力学模型赋值参数表

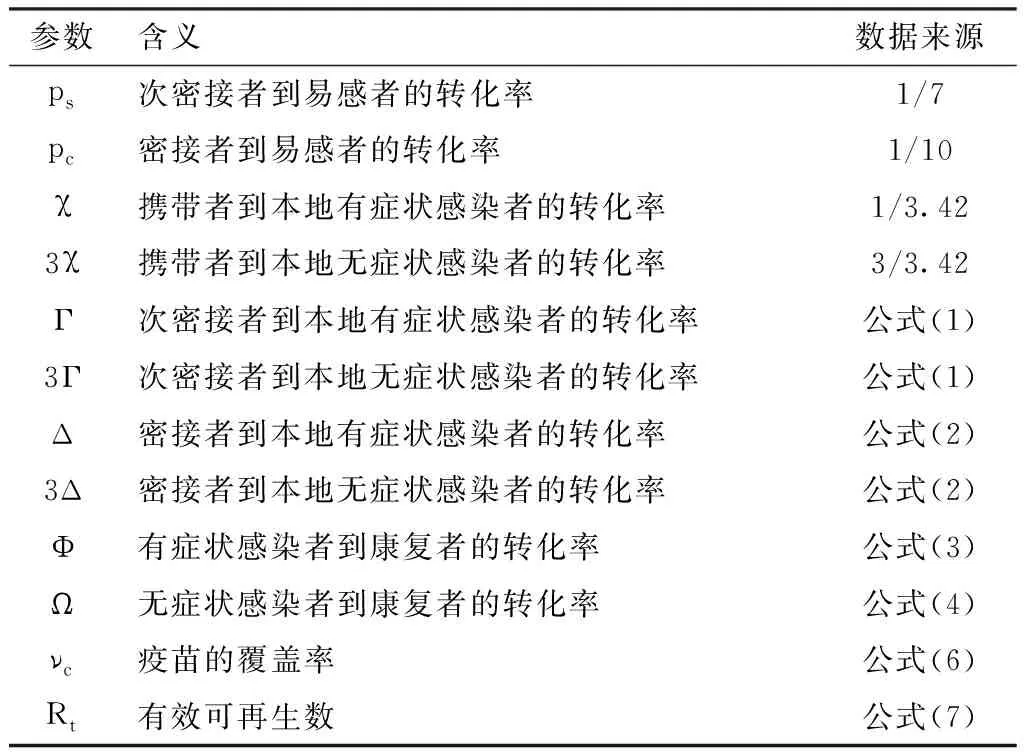
表2 改进SEIR动力学模型干预函数参数表

表3 改进SEIR动力学模型拟合参数表

为了使模型具有普适性,本文首先依据2022年6月28日发布的《新型冠状病毒肺炎诊疗方案(试行第九版)》的具体防控政策指导,对传统SEIR模型进行了相关改进。设置次密接者的居家健康监测时长为α天。设置密接者的集中隔离时长为β天,居家健康监测时长为γ天。设置有症状感染者的最低集中隔离时长为ϑ天和居家健康监测时长为π天。设置无症状感染者的最低集中隔离时长为κ天和居家健康监测时长为ξ天。已知群组状态到有症状感染者和无症状感染者的转化率均服从与时间相关的指数分布。

于是,本文的次密接者到本地有症状感染者的转化率公式(1),密接者到本地有症状感染者的转化率公式(2),有症状感染者到康复者的转化率公式(3)和无症状感染者到康复者的转化率公式(4)。

P(Γ=t)=α*e-αt

(1)

P(Δ=t)=(β+γ)*e-(β+γ)t

(2)

P(Φ=t)=(ϑ+π)*e-(ϑ+π)t

(3)

P(Ω=t)=(κ+ξ)*e(κ+ξ)t

(4)

文献研究表明[31],受奥密克戎毒株影响的次密接者到易感者的转化率可设定为ps=1/α。同理,设定密接者到易感者的转化率pc=1/(β+γ),设定携带者到本地有症状感染者的转化率χ=1/ρ。此外, 根据国家卫生健康委员会公布的数据,拟合得到基于奥密克戎的无症状感染者每日增速大约是有症状感染者增速的3倍,故设定携带者到本地无症状感染者的转化率3χ=3/ρ,同样适用于密接者到本地无症状的转化率3Δ和次密接者到本地无症状的转化率3Γ。

RMSE=RMSE1+RMSE2+RMSE3

(5)

最后,根据相关文献基础研究人工干预程度W、疫苗覆盖率[27]νc及疫苗接种率[28]σ与携带者之间的关系。首先初始拟合ε和得到权重参数w0和w1,其次研究疫苗接种率和人工干预程度对疫情发展趋势的影响,本文给出如下相应的数学逻辑关系:

(6)

(7)

(8)

(9)

为了检验改进模型与真实数据的拟合程度,本文采用国家卫生健康委员会公布的中国2022年8月1日-8月20日的密接者、次密接者及康复者等疫情数据进行拟合(如图2所示);2022年8月1日-8月20日有症状感染者和无症状感染者等疫情数据进行模型可靠性验证(如图3所示);进一步预测了2022年8月21日-8月25日的密接者、次密接者、康复者、有症状感染者和无症状感染者的变化情况(如图2和图3所示)。 通过图3预测数据与真实疫情数据对比表明,改进的SEIR动力学模型对疫情走势的评估与真实疫情数据的走势是基本一致的,可为利用MATLAB生成的数字化应急预案中的防控政策提供理论依据。

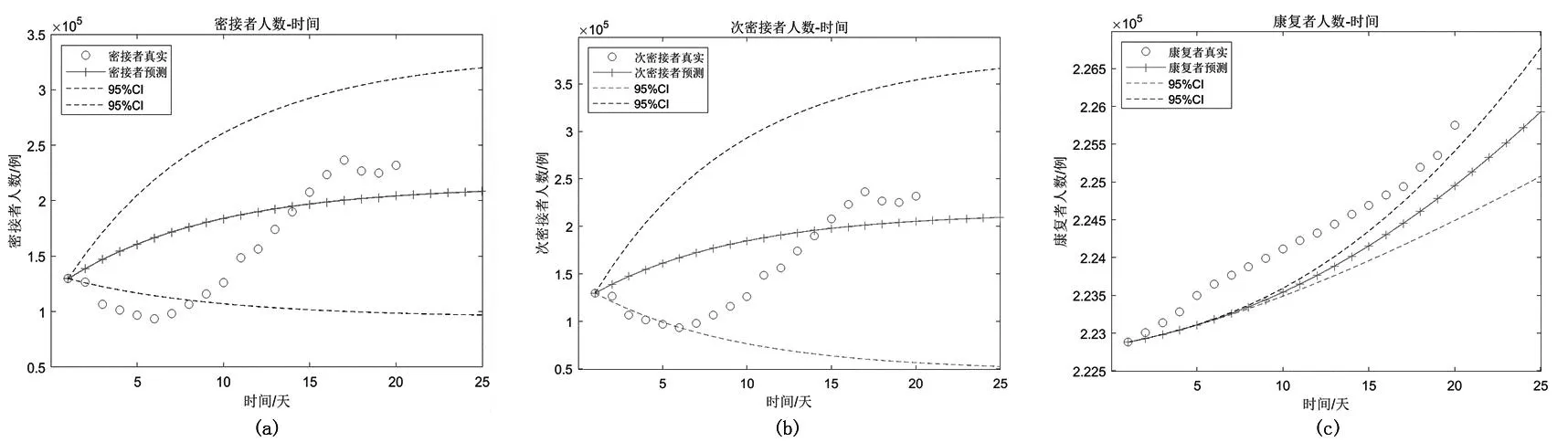
图2 次密接者(a)、密接者(b)以及康复者(c)随时间变化情况

图3 无症状感染者(a)和无症状感染者(b)随时间变化情况

2 结果

本文以我国真实疫情数据为基础,采用MATLAB2022a软件,搭建真实的数字化实验环境,生成应急预案的政策内容,分别为携带者、密接者、次密接者、本地有症状和本地无症状感染者提供防控政策建议和医疗资源配置优化方案。

2.1 携带者对核酸检测频率、疫苗接种率、人工干预强度的影响分析

图4(a)展示了携带者随时间的变化关系,图4(b)研究了疫苗接种率对携带者的影响。奥密克戎变种的平均潜伏期为3.4天,所以本研究将本地第n天的新增感染者设置为(n-3)天的携带者数量,并将其作为衡量疫情是否会大爆发的关键参考阈值。已知我国截止到2022年9月的两针疫苗接种率达89.7%[31],三针疫苗接种率达70.0%[28];根据群体免疫的疫苗覆盖率公式(6)可知,疫苗接种率至少要89.5%以上才能实现群体免疫;图4(b)显示疫苗接种率达到89.7%时,8月20日的本地隐匿传播携带者为1 215例,8月25日携带者数量达1 452例。这一方面表明此时疫情仍然处于爆发上升期,并未到达拐点,应继续加大核酸检测频率。另一方面,图4(b)与图4(a)对比可知,图4(a)显示8月20日携带者数量应达1 433例,大约比图4(b)预测值高218例,这是由于每个机体对疫苗的反应不同,导致部分易感者接种疫苗后并未产生抗体,从而使携带者预测数量偏低。此外,图4(b)表明我国截止2022年9月的实际疫苗接种率大约在85.0%到89.7%之间,因此,需要进一步采取激励机制提高疫苗接种率。若提高疫苗接种率达89.7%水平线,携带者数量可减少约15.7%。若采取相关激励措施提升疫苗接种率达到95.0%及以上,携带者数量最高可减少53.6%。

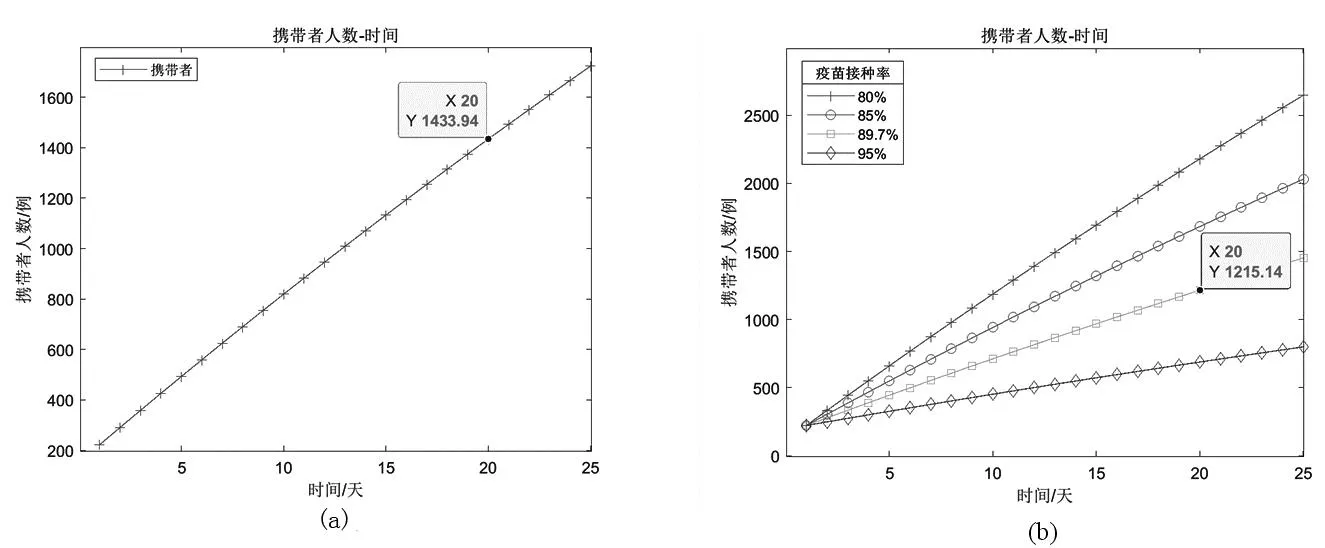
图4 携带者人数变化情况(a)和疫苗接种率分析(b)

图5量化了人工干预强度和携带者数量间的逻辑关系。在人工干预强度加倍的情况下,携带者数量最多可降至953例。若将人工干预强度减半,携带者数量将增至3263例。

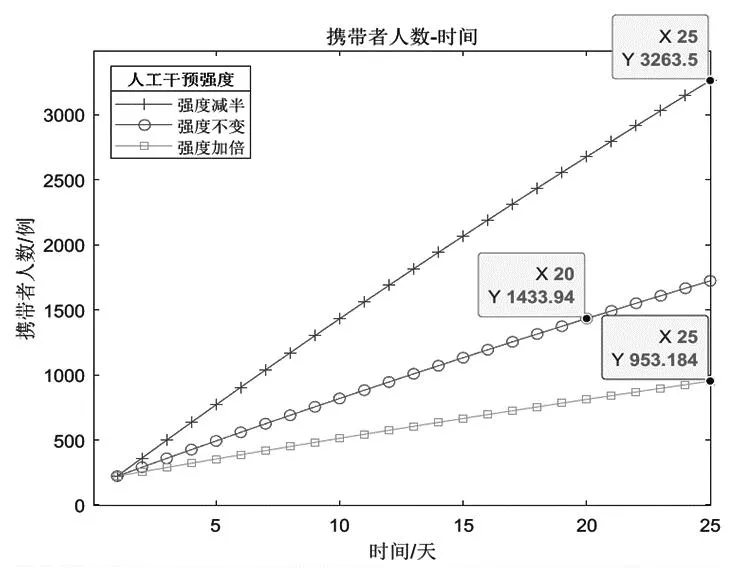
图5 人工干预强度分析

2.2 密接者/次密接者的隔离政策分析

图6(a)分析了密接者的隔离政策和隔离房间之间的定量关系。当对密接人员采取7日集中隔离+3日居家健康监测时,8月20日需配置约204 332间隔离房间,8月25日接近疫情发展的最高拐点时配置约208 403间隔离房间。如果将隔离政策调整为3日集中隔离+2日居家健康监测,8月25日将最多需要配置201 824间隔离房间。若将隔离政策调整为14日集中隔离+6日居家健康监测,8月25日将需最多配置211 831间隔离房间。图6(b)分析了针对次密接者的隔离政策与隔离房间的定量关系。当对次密接人员采取7日居家健康监测时,8月20日约现存205 306例次密接,8月25日接近疫情发展的最高拐点时约现存209 431例次密接。

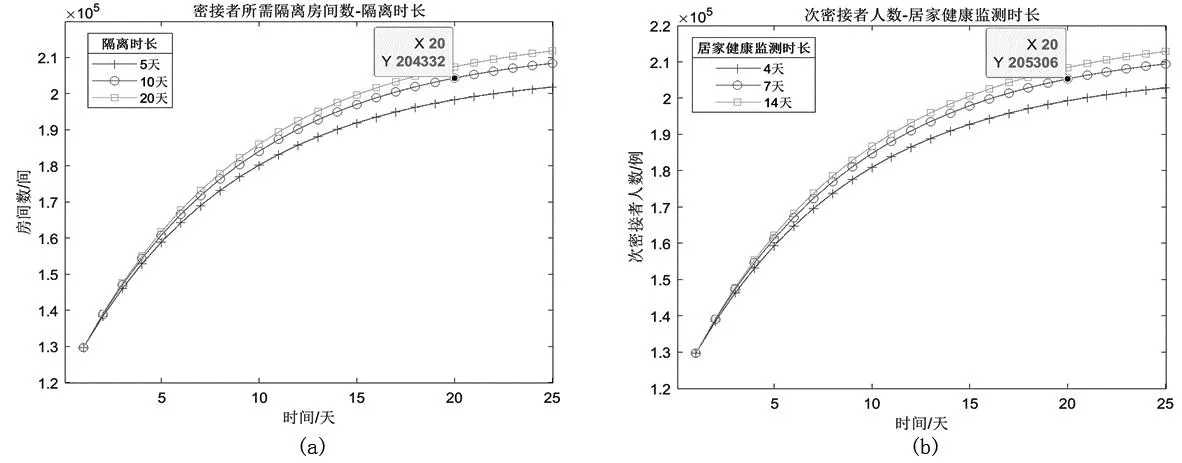
图6 隔离政策对隔离房间的需求分析(a)和对次密接者的影响分析(b)

若将隔离政策调整为4日居家健康监测,8月25日约现存202 822例次密接。若将隔离政策调整为14日居家健康监测,8月25日约现存212 874例次密接。综上可知,图6(a)可指导密接者的隔离房间、隔离方舱、志愿者、医护人员和医用物资等的提前配置;假若次密接者也采取集中隔离政策,图6(b)亦可指导其相应医疗资源的配置;若采取居家健康监测的政策,图6(b)也可引导社区提前做好次密接人员的安置工作。

图7展示了密接者与次密接者的隔离政策工作对疫情发展趋势的影响。在与现行的《新型冠状病毒肺炎诊疗方案(试行第九版)》中针对隔离要求的比对中发现,当对密接人群采取14日集中隔离+6日居家健康监测,次密接人群采取14日居家健康监测时,本地有症状感染者将最多下降60.0%,本地无症状感染者将最多下降55.0%,效果显著。

图7 隔离政策对本地无症状感染者(a)和本地有症状感染者(b)的影响分析

2.3 本地感染者的医院治疗政策分析

图8分析了本地感染者(本地有症状和无症状的统称)的医院床位数需求。8月20日,有症状和无症状感染者分别需要13 545和15 673张床位,随着疫情的发展,8月25日共需床位约35 354张。预测结果显示,既可根据预测结果提前5天内为有症状额外准备4 132张床位,还需要为无症状额外准备2 004张床位。

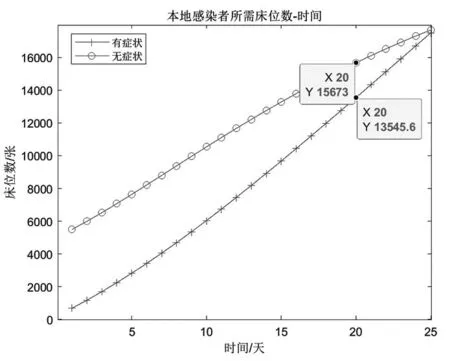
图8 本地感染者对医院床位数的需求分析

图9(a)分析了医院治疗政策对本地无症状感染者的床位数的影响,图9(b)分析了医院治疗政策对本地有症状感染者的床位数的影响。由图可见,对有症状感染者和无症状感染者采取14天或21天集中治疗的结果差别有限,因此,从节约医疗资源的角度分析,采取14天的集中救治更为合适。但是,若对无症状感染者和有症状感染者统一采取7天集中救治政策,相比于采取14天的集中救治,最多可分别节约5.8%和7.6%的床位数。考虑我国医院床位数较为紧张,众多其它疾病需要住院治疗,因此,研究建议采取最低时长的医院救治政策。

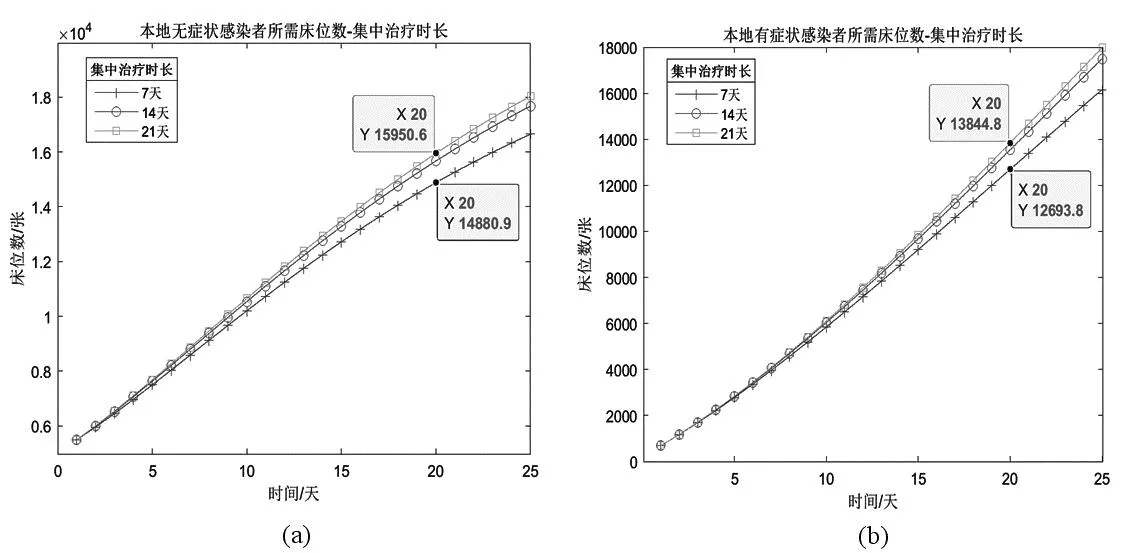
图9 医院治疗政策对本地无症状感染者床位数(a)和本地有症状感染者床位数(b)的需求分析

3 讨论

首先,本研究在对携带者对核酸检测频率、疫苗接种率、人工干预强度的影响分析中发现,作为抗击疫情较为有效的策略,疫苗接种率的提升不仅能降低疫情扩散的风险,还可节约大量核酸检测、隔离观察和医疗治疗等相关费用。该结论为国家自2022年下半年以来持续推动新冠疫苗接种这一举措提供了科学依据。与此同时,国家卫生健康委于2023年1月6日发布的《新型冠状病毒感染诊疗方案(试行第十版)》中提出,为方便感染者进行快速自我检测和自我隔离,方案在核酸检测的基础上增加抗原检测阳性作为诊断标准[33]。这一举措不仅节约了核酸检测的相关费用,也显著减少了隔离观察和就医治疗等公共资源的使用。其次,本研究通过量化密接者/次密接者的隔离政策和实际需求,如密接者的隔离房间、隔离方舱、志愿者、医护人员和医用物资等,证明了早期的隔离政策在控制感染人数上虽更为有效,但会导致疫情管控成本增加。对于需要住院治疗的感染者,建议采取最低时长的医院救治政策。这些结论和建议也在第十版方案中得到了较好的验证。

本文也存在一些不足之处。首先,动力学模型存在数学假设非常严格等固有缺陷,无法充分捕捉各种防控措施的动态细节变化。复杂的实际情况也导致数学模型对现实世界疫情的预测能力有一定的局限性。另外,拟合数据也有一定限制,如模型拟合时间太短所导致的相关参数不确定性和敏感性较高。未来,研究将会扩展时间广度更高的疫情数据,进一步探索更多拟合算法,降低局限性,提高模型预测精度。

4 结语

本文针对传统公共卫生(重大疫情)应急预案的制定受时效和使用场景限制等问题,探索了如何通过基于改进SEIR模型的数字化技术在应急预案制定中的应用,以突破传统应急预案制定的瓶颈。研究参考《新型冠状病毒肺炎诊疗方案(试行第九版)》的具体防控政策,对传统SEIR模型参数和使用场景进行了相关改进,针对核酸检测、疫苗接种、人工干预、隔离政策、医院救治政策等进行了普适性建模,搭建了基于MATLAB的数字化实验环境,验证了《新型冠状病毒肺炎诊疗方案(试行第九版)》预案中的防控政策可通过基于改进SEIR模型的数字化技术生成和更新。本文不仅为疫情防控政策提供了科学理论支撑,还搭建了应急预案的数字化生成平台,以提高重大疫情应急预案的实用性。