长江经济带农业绿色发展水平测度及联动效应研究

杨浩然

(西南政法大学,重庆 401120)

推动长江经济带发展是党中央作出的重大决策,是关系国家发展全局的重大战略。 党的十八大以来,习近平总书记多次赴长江沿线省市考察调研,强调“把修复长江生态环境摆在压倒性位置,共抓大保护,不搞大开发”①习近平:《在深入推动长江经济带发展座谈会上的讲话》,载《求是》2019 年第17 期,第4 页。。 随着《长江经济带发展规划纲要》的实施,长江经济带生态环境逐年改善,但同时也存在着渔业资源衰退、农业面源污染治理难度大等问题。②参见曹立、郭兆晖编著:《讲述生态文明的中国故事》,人民出版社2020 年版,第74-80 页。传统的农业生产是一把双刃剑,既是长江流域面源污染的重要来源之一③参见金书秦、张哲晰、胡钰、韩冬梅、杜志雄:《中国农业绿色转型的历史逻辑、理论阐释与实践探索》,载《农业经济问题》2023 年第8 期,第142 页;饶静、许翔宇、纪晓婷:《我国农业面源污染现状、发生机制和对策研究》,载《农业经济问题》2011 年第8 期, 第81-82 页。,也提供了重要的生态产品和服务。④See JunJie Wu & Bruce A. Babcock, Contract Design for the Purchase of Environmental Goods from Agriculture, 78 American journal of agricultural economics 935, 935-945(1996).因此,要修复长江经济带的生态环境,必须要转变农业生产方式,推动长江经济带农业生产整体向绿色转型。 这就需要在地区之间形成合力,协同推进长江经济带内不同地区的农业绿色发展。①参见成长春、徐长乐等:《推动长江经济带发展重大战略研究》,人民出版社2021 年版,第785-786 页。因此,如何从区域协同和联动的视角提高长江经济带农业绿色发展质量,就成为解决长江流域生态环境难题、实现长江经济带高质量发展的现实途径。

目前,长江经济带绿色发展的联动机制仍不健全。②参见何立峰:《扎实推动长江经济带高质量发展》,载《宏观经济管理》2019 年第10 期,第1-4 页。现有的研究虽然对如何推动农业绿色发展进行了深入的探索③参见李守伟、李光超、李备友:《农业污染背景下农业补贴政策的作用机理与效应分析》,载《中国人口·资源与环境》2019 年第2期,第98 页;马贤磊、车序超、李娜、唐亮:《耕地流转与规模经营改善了农业环境吗? ——基于耕地利用行为对农业环境效率的影响检验》,载《中国土地科学》2019 年第6 期,第63 页;夏秋、李丹、周宏:《农户兼业对农业面源污染的影响研究》,载《中国人口·资源与环境》2018 年第12 期,第132 页。,但仍存在两个方面的不足:一是对于农业绿色发展水平的衡量还不够合理;二是对于如何推动长江经济带不同地区间的农业绿色联动发展关注较少。 对此,本文在回顾现有研究中农业绿色发展水平衡量方法的基础上,重新构建了农业绿色发展水平的评价指标体系及其评价方法。 然后利用2003-2020 年间长江经济带的城市数据对地区间农业绿色发展水平的收敛和空间溢出效应进行测度。 分析结果,长江经济带总体的农业绿色发展水平在持续地提升,并且城市间的差距在不断缩小,城市间农业绿色发展水平的收敛趋势明显。 但随着各城市间农业绿色发展水平的趋同,城市农业绿色发展的空间溢出效应逐渐消失。 因此,在后期,长江经济带农业绿色发展的整体性更多依靠各城市自身的内生动力实现,而不是依靠空间溢出效应。

一、文献综述

农业绿色发展的理念在我国源远流长。 《吕氏春秋·审时》有谓:“夫稼,为之者人也,生之者地也,养之者天也。”也就是说,农业生产要遵循天地人三才之道,人作为主动的一方需要考量生态环境的承载能力,农业生产不应以破坏环境为代价。④参见秦晓:《论〈吕氏春秋〉的农学思想及其生态价值》,载《宝鸡文理学院学报(社会科学版)》2022 年第1 期,第40 页。因此,农业生产应以绿色为导向,实现人与自然之间关系的平衡。 党的十八大以来,我国高度重视绿色发展。 按照“绿水青山就是金山银山”这一发展理念,农业绿色发展可以被解释为是对于水土资源的保护,特别是水土资源质量的保护⑤参见于法稳:《新时代农业绿色发展动因、核心及对策研究》,载《中国农村经济》2018 年第5 期, 第19 页。,其路径不仅包括要素间的匹配这一横向系统,还包括不同产业间、农业生产各环节间的纵向衔接。⑥参见张林秀、白云丽、孙明星、徐湘博、何加林:《从系统科学视角探讨农业生产绿色转型》,载《农业经济问题》2021 年第10 期,第43 页。

目前,文献中存在两种衡量农业绿色发展水平的方法。 一种是通过构建农业绿色全要素生产率(GTFP)增长指数来衡量一个地区的农业绿色发展水平。 目前,测算农业GTFP 增长率主要采用的是以数据包络分析(DEA)为基础的非参数方法,如方向距离函数⑦参见杨骞、王珏、李超、刘鑫鹏:《中国农业绿色全要素生产率的空间分异及其驱动因素》,载《数量经济技术经济研究》2019 年第10 期,第28 页;郭海红、刘新民:《中国农业绿色全要素生产率的时空分异及收敛性》,载《数量经济技术经济研究》2021 年第10 期,第71页。、SBM(slack-based measure)模型①参见李谷成:《中国农业的绿色生产率革命:1978—2008 年》,载《经济学(季刊)》2014 年第2 期,第540 页。、Super-SBM 模型②参见孟祥海、周海川、杜丽永、沈贵银:《中国农业环境技术效率与绿色全要素生产率增长变迁——基于种养结合视角的再考察》,载《农业经济问题》2019 年第6 期,第12 页;刘亦文、欧阳莹、蔡宏宇:《中国农业绿色全要素生产率测度及时空演化特征研究》,载《数量经济技术经济研究》2021 年第5 期,第46 页。、EBM(epsilon-based measure)模型③参见金绍荣、任赞杰:《乡村数字化对农业绿色全要素生产率的影响》,载《改革》2022 年第12 期,第108 页;王菲、孙淑惠、刘天军:《数字经济发展推进了农业生产方式变革吗——来自黄河流域地级市的证据》,载《中国农村经济》2023 年第9 期,第125 页。。 在这些模型中,非期望产出是通过将投入的使用数量乘以一个系数得到的,也就是说,在非期望产出和投入之间存在一个物质平衡恒等式关系。④See Finn R. Førsund, Performance Measurement and Joint Production of Intended and Unintended Outputs, 55 Journal of Productivity Analysis 157, 157-175(2021).农业GTFP 增长率本质上衡量的是同时缩减非期望产出和投入的综合水平。 但不论是SBM 模型和EBM 模型,还是方向距离函数模型,在测算GTFP 增长率时都无法确保缩减的非期望产出和投入之间是满足物质平衡恒等式关系的。 因而可能会导致测算的农业GTFP 增长率不符合物质平衡恒等式。 采用GTFP 增长率来衡量农业绿色发展水平还存在另外一个缺陷,即增长率本身并不代表发展水平,除非是采用农业GTFP 的绝对水平,而不是增长率。 而上述几种方法只能根据Malmquist 指数法或者Malmquist-Luenberger 指数法来得到GTFP 的增长率。

另一种是构建一个衡量农业绿色发展的指标体系,然后根据熵权法得到一个农业绿色发展水平综合得分。 比如,可以从乡村振兴的角度采用产业兴旺、生态宜居等6 个方面的指标构建农业绿色发展水平测度指标体系⑤参见赵锐、卢弍林、毛尚熠:《共同富裕视域下我国老年群体收入差距的调节机制探析》,载《社会治理》2023 年第4 期,第107 页。,或可以从农业资源节约、农业环境治理、农业生产效益3 个维度来测算各地级市的农业绿色发展水平。⑥参见姚鹏、李慧昭:《农业水权交易能否推动农业绿色发展》,载《中国农村经济》2023 年第2 期,第22 页。采用综合指数法测算农业绿色发展水平的文献往往包含了过多的指标。 其中一些指标可能与农业绿色发展并无直接的关联,如农村居民人均住房面积、人均用电量等指标也被加入了农业绿色发展水平的衡量体系当中。⑦参见唐健飞、刘剑玲:《省域农业可持续发展水平评价及其耦合协调分析——以长江经济带11 省市为例》,载《经济地理》2022 年第12 期,第181 页。另一些指标可以被认为是对农业绿色发展有影响的变量,而不是表示农业绿色发展水平的变量,如城乡人均收入比、农村教育状况、农村医疗状况等指标。 这不仅使得农业绿色发展水平的衡量不够精确,也混淆了农业绿色发展和以上事实的因果关系。

测度农业绿色发展的研究很多,但鲜有关于农业绿色发展区域联动的研究,大多数研究主要关注的是农业生产的空间布局。 例如,采用外部性理论研究土地经济效益在空间上的分布。⑧参见王丹、黄季焜:《草原生态保护补助奖励政策对牧户非农就业生计的影响》,载《资源科学》2018 年第7 期,第1348 页。其中,土地经济效益的空间差异反映了农业生产在空间分布上的差异和相关性。 屠能圈是早期关于农业生产在空间上布局的理论。 根据农业空间布局理论,农业在空间上的分布不仅会影响水资源的利用效率和用水量⑨参见王秀鹃、胡继连:《中国农业空间布局与农业节水研究》,载《山东社会科学》2019 年第2 期,第133 页。,而且会影响农业提供的生态服务价值。⑩See Joshua J. Lawler, David J. Lewis, Erik Nelson, Andrew J. Plantinga, Stephen Polasky, John C. Withey, David P. Helmers,Sebastián Martinuzzi, Derric Pennington & Volker C. Radeloff, Projected land-use change impacts on ecosystem services in the United States, 111 PNAS 7492, 7492-7497(2014).因此,农业生产的空间布局会影响地区的生态系统,从而对于地区的总体绿色发展水平产生影响。 也就是说,农业绿色发展会呈现出区域内的联动性。 但目前,还没有研究对长江经济带农业绿色发展的空间联动性是否存在以及时空变化趋势进行探索。

通过对相关文献的梳理可以发现,目前对于农业绿色发展的测度仍需改进,相关研究更多的是停留在对农业绿色发展影响因素的探索,较少有研究从区域联动的视角探索农业绿色发展的推进路径。

二、研究方法及数据

(一)农业绿色发展水平的衡量

本文并不试图建立庞大而繁杂的指标体系,而是选择少数能够直接反映农业绿色发展水平的指标来构建一个衡量农业绿色发展水平的综合指数。 农业绿色发展不仅要降低农业生产中的环境污染物排放量,同时也需要提高农业生产效率。 在碳达峰碳中和的背景下,农业向环境排放的污染主要来自于农药、化肥以及农机使用的燃料油。①其他污染来源还应该包括塑料薄膜等,但由于数据可得性的限制,暂未将其他指标列入。各指标的定义及其选择依据参见表1。 需要注意的是,这里并没有使用各指标的绝对数量来衡量一个地区的农业绿色发展水平。 因为不同地区间的农业生产规模有较大的差异,如果只比较不同地区的农业产值、化肥农药等投入的绝对数量,并不能真正反映地区间的农业绿色发展水平差异。 因此,本文是从生产效率的角度来衡量农业绿色发展水平,即农业劳动生产率、机械生产率、农药化肥生产率等。

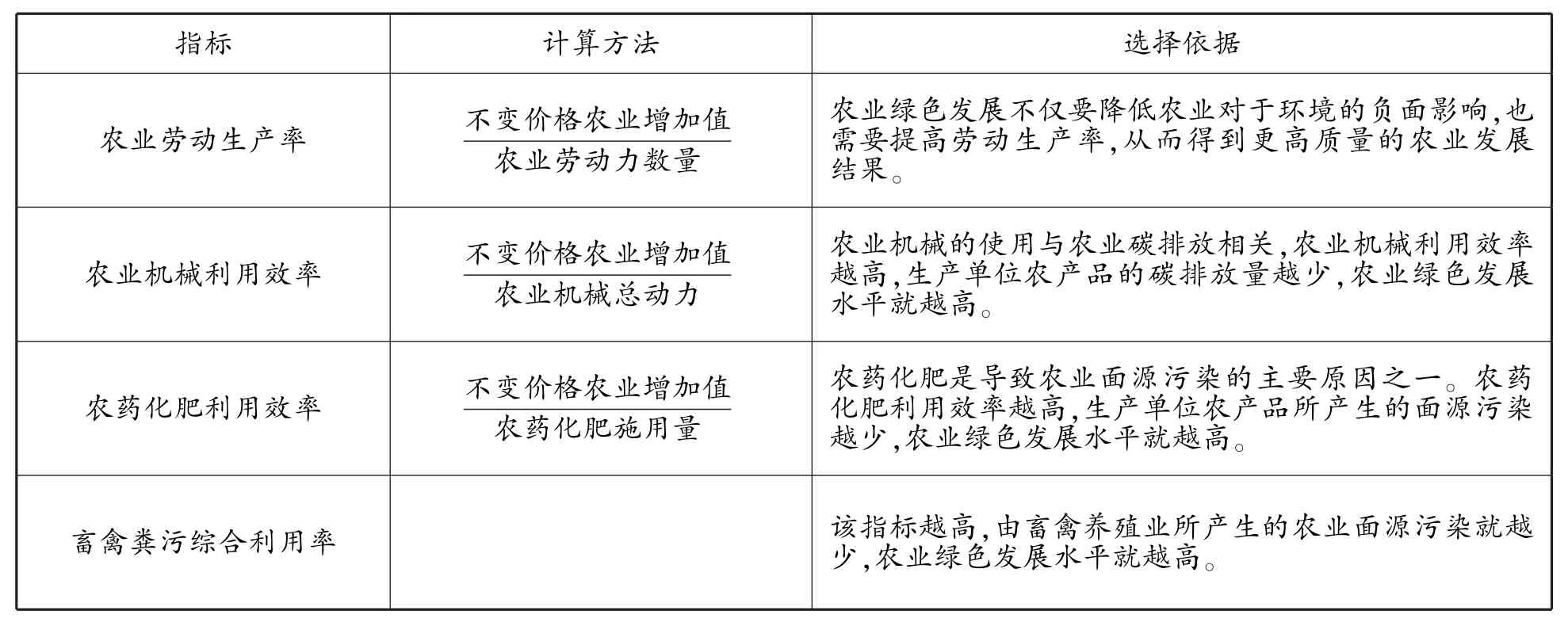
表1 农业绿色发展指标

对于其他指标,如对生活污水和生活垃圾进行处理的行政村占比、卫生厕所普及率、农村绿化率等,虽然可能与农业绿色发展水平相关,但这种关联更多是间接的影响,而不是直接表征农业绿色发展水平。 因此,本文并未将此类变量加入到衡量长江经济带农业绿色发展的指标体系当中。

(二)Dagum 基尼系数及分解

将长江经济带划分为上游、中游、下游三个区域。 利用Dagum 基尼系数测算长江经济带农业绿色发展的总体差异,然后再将其分解为区域内差异、区域间差异和区间超变密度贡献。①See Camilo Dagum, A New Approach to the Decomposition of the Gini Income Inequality Ratio, 22 Empirical Economics 515, 515-531(1997).

其中,G代表Dagum 基尼系数,M表示区域个数(M= 3,即长江经济带的上、中、下游三个区域),N代表长江经济带地级市个数,Ni和Nj分别表示区域i和区域j中地级市的个数。yik表示第i个区域中第k个地级市的农业绿色发展水平,代表长江经济带所有地级市的平均农业绿色发展水平。

G可以进一步分解为:

区域间基尼系数总贡献Ggb又可以分解为:

(三)空间相关性检验

本文采用全局Moran's I 指数和Moran 散点图对长江经济带中地级市的农业绿色发展水平的空间相关性进行初步分析。 全局Moran's I 指数可以对长江经济带中所有城市的农业绿色发展水平的空间相关性做出判断,Moran 散点图则关注长江经济带农业绿色发展水平在局部的空间相关性。判断空间相关性是模型设定的基础,如果存在空间相关性而没有在绝对收敛和相对收敛的回归模型中进行控制,就会导致模型设定偏误问题。①See Luc Anselin, Spatial Econometrics: Methods and Models,Springer,2013, p.16-17.

(四)农业绿色发展水平收敛性检验

协同推进长江经济带农业绿色发展取决于两个方面的因素。 第一个是农业绿色发展水平的收敛性,即农业绿色发展水平较低的地区是否能够不断地向农业绿色发展水平高的地区靠拢。 第二个是农业绿色发展的空间溢出效应。 空间溢出效应决定了农业绿色发展水平高的地区是否对邻近地区的农业绿色发展具有带动作用。

经济学中的收敛性分为绝对收敛和相对收敛。②参见彭国华:《中国地区收入差距、全要素生产率及其收敛分析》,载《经济研究》2005 年第9 期,第19-20 页。其中,绝对收敛是指地区间的农业绿色发展水平差异是否会“自动”消失。 绝对收敛的衡量方法可以分为两类,第一类是衡量横截面单位的农业绿色发展水平的分散程度是否会随时间的变化而缩小,该方法一般被称为“σ绝对收敛”,这是因为所构建的收敛指标主要依赖于目标变量的标准差。 常用的σ绝对收敛衡量指标包括标准差、变异系数等。 本文采用变异系数来衡量长江经济带不同城市之间的农业绿色发展水平的差异。 第二类方法则主要是衡量农业绿色发展水平较低的地区是否具有更快的农业绿色发展水平增长速度,检验方法是采用以下回归模型:

其中,yi,t表示城市i在年份t的农业绿色发展水平,α和β为待估参数,ε为随机误差项。 当β< 0 时,绝对收敛假说成立,也就是k个时期之后的农业绿色发展水平增长率和初始时期的农业绿色发展水平呈负相关关系。

模型(1)定义的收敛也被称为“β绝对收敛”。 其中k的选择对于β绝对收敛的估计十分重要。在实证研究中,以2003 年为基期,分别设定2010 年、2015 年、2020 年三个终点时期,以检验β的估计结果是否会受到k的选择的影响。

模型(1)本质上是一个横截面数据模型。 横截面数据模型的缺点在于无法控制个体效应。 在本文的实证研究中,控制长江经济带城市的个体效应十分有必要。 因为地级市的一些独有的特点(如长江上游地区和中下游地区的地理环境、自然条件有很大的差别)既可能会影响该地区的农业绿色发展水平,又可能会影响农业绿色发展水平增长率。 在截面数据模型中,无法处理这些个体效应导致的内生性问题。 因此必须为模型(1)寻找合适的工具变量才能得到关于β的一致估计结果。

使用面板数据可以部分解决遗漏变量导致的内生性问题。 对此,可以构建条件收敛假说模型:

在模型(2)中,Δlnyit表示农业绿色发展水平对数的组内一阶差分,lnyi,t-1表示农业绿色发展水平的组内一阶滞后,β是条件收敛系数。 对比模型(1)和模型(2)可以发现,条件收敛模型并非是绝对收敛模型从截面数据向面板数据的简单扩展,而是对模型设定做出了很大的调整。 在条件收敛模型中,β衡量的是t- 1 个时期的农业绿色发展水平对于t- 1 到t的农业绿色发展水平增长率的影响。 而在绝对收敛模型中,β衡量的是初始时期的农业绿色发展水平对于整个时间段的农业绿色发展水平增长率的影响。 因此,两个模型所衡量的农业绿色发展水平收敛的时间范畴是不同的。绝对收敛模型的参数β衡量的是整个时间段收敛程度的累积,而相对收敛模型的参数β衡量的是每单位时间跨度(每年)收敛程度的平均增量。 在对比绝对收敛模型和条件收敛模型的β估计值时,需注意到这种概念上的差异。ui衡量的是不可观测的个体效应,vit是不可观测的随机扰动。zit表示其他的控制变量,包括农村人均可支配收入、农业增加值占比、农村人均受教育水平、城乡收入差距、恩格尔系数、城镇化率、政府支出占GDP 比重等。γ为相应的待估参数向量。

(五)农业绿色发展的空间效应

如果农业绿色发展水平存在空间依赖,而没有在模型中表示出来,就会形成模型设定偏误。 以相对收敛模型为例,可以将一个一般化的空间面板数据模型表示为①See Federico Belotti, Gordon Hughes & Andrea Piano Mortari, Spatial Panel-Data Models Using Stata, 17 The Stata Journal 139, 139-180(2017).:

其中W为空间权重矩阵,本文采用的是地理距离矩阵,城市之间的距离采用经纬度计算得到。②参见王守坤:《空间计量模型中权重矩阵的类型与选择》,载《经济数学》2013 第3 期,第59 页。对回归模型(3)和(4)进行不同的设定,可以得到不同的空间效应模型。 如果令θ=0,λ=0,则变为空间滞后(Spatial autoregressive,SAR)模型;如果令θ= 0,则变为空间滞后加空间自相关(spatial autocorrelation,SAC)模型;如果令λ= 0,则变为空间杜宾模型(Spatial Durbin Model,SDM)。 虽然还有其他的空间计量模型,但本文只考虑这三种形式的变化。 对绝对收敛模型也采取相同的设定。

(六)数据来源

本文所用数据来自于长江经济带各省份以及地级市的统计年鉴。 在整理数据时,首先通过省级统计年鉴中分地区的数据来构建相关的变量。 如果省级年鉴的相关数据缺失,则通过对应地级市的统计年鉴进行查找。 最终获得长江经济带2003-2020 年间106 个城市的数据,其中包括上海和重庆两个直辖市和其他104 个地级市。

三、实证分析结果

(一)长江经济带城市农业绿色发展水平的评价

表2 中给出了2003-2020 年间长江经济带各城市的农业绿色发展水平测算结果分年度的描述性统计量。 可以发现,城市平均的农业绿色发展水平在逐年上升,反映了长江经济带农业绿色发展质量的改善。 从最大最小值的统计可以发现,样本中并没有极端值,也就是没有农业绿色发展水平过高或者过低的城市。 此外,2003-2020 年间农业绿色发展水平的最小值和最大值总体上均展现出增长的趋势,这反映了长江经济带农业绿色发展水平的提升是总体性的、全局性的,而不是只集中在少数地区。

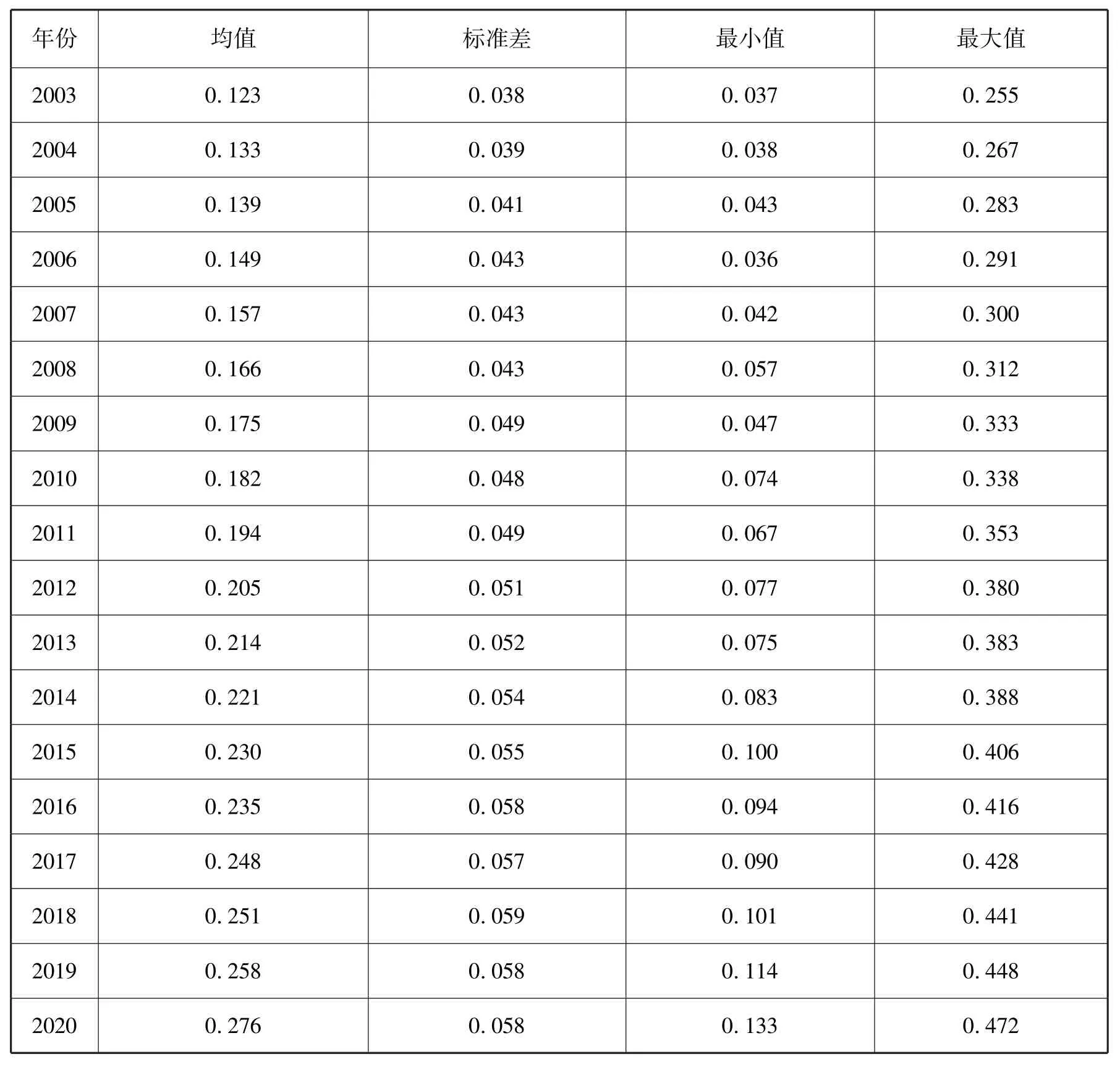
表2 长江经济带各地级市农业绿色发展水平的描述性统计(2003-2020)

(二)Dagum 基尼系数及分解

图1 给出的是用基尼系数衡量的长江经济带总体和分地区(上、中、下游三个地区)的农业绿色发展水平差异。 可以发现,从总体上看,长江经济带各城市间的农业绿色发展水平差异在不断地缩小。 但在不同的区域,Dagum 基尼系数的变化趋势不同。 其中,上游和下游地区Dagum 基尼系数下降趋势明显,表明在这两个区域城市间的农业绿色发展水平的差异在不断地下降。 而在中游地区,2003-2018 年间的Dagum 基尼系数基本保持稳定不变,而在2019 年和2020 年,Dagum 基尼系数有突然的升高。 对于长江经济带总体的Dagum 基尼系数,区域间差异和区域内差异的贡献占绝大多数,超变密度的贡献较少。 其中,除2019 和2020 年之外,区域间差异是长江经济带农业绿色发展水平差异的主要来源。 2019 和2020 年的变化可能主要是由于中游地区Dagum 基尼系数的突然上升所导致的。 可以发现,在这两年,三个区域的Dagum 基尼系数相差不大。 因此,长江经济带农业绿色发展水平的总体差异主要就体现为区域内差异,区域间的差异基本上消除了。

图1 长江经济带农业绿色发展水平Dagum 基尼系数及分解

(三)空间相关性和σ 绝对收敛

从图2 的可以发现,用变异系数衡量的长江经济带城市之间的农业绿色发展水平在不断收敛,城市间的农业绿色发展水平差异在不断缩小。 变异系数除了在2009 年(即全球金融危机之后的一年)有明显向上的跳跃之外,总体上呈现下降的趋势。 同时,Moran's I 指数显示,长江经济带中城市的农业绿色发展水平在空间上的关联也在逐渐减弱。 虽然Moran' s I 指数的波动要强于变异系数,但其下降的趋势也更加明显。 从2019 年开始,Moran's I 指数下降到小于0.1。 到2020 年,Moran' I指数已经降为0.07,虽然仍是显著的,但空间相关性已经非常弱了。 地区间差异的收敛和空间相关性减弱的同步性也出现在其他情况中。①See Sergio J. Rey & Brett D. Montouri, Us Regional Income Convergence: A Spatial Econometric Perspective, 33 Regional Studies 143,143-156(1999).长江经济带农业绿色发展水平空间相关性的减弱可以通过分析更详细的局部空间相关性来解释。

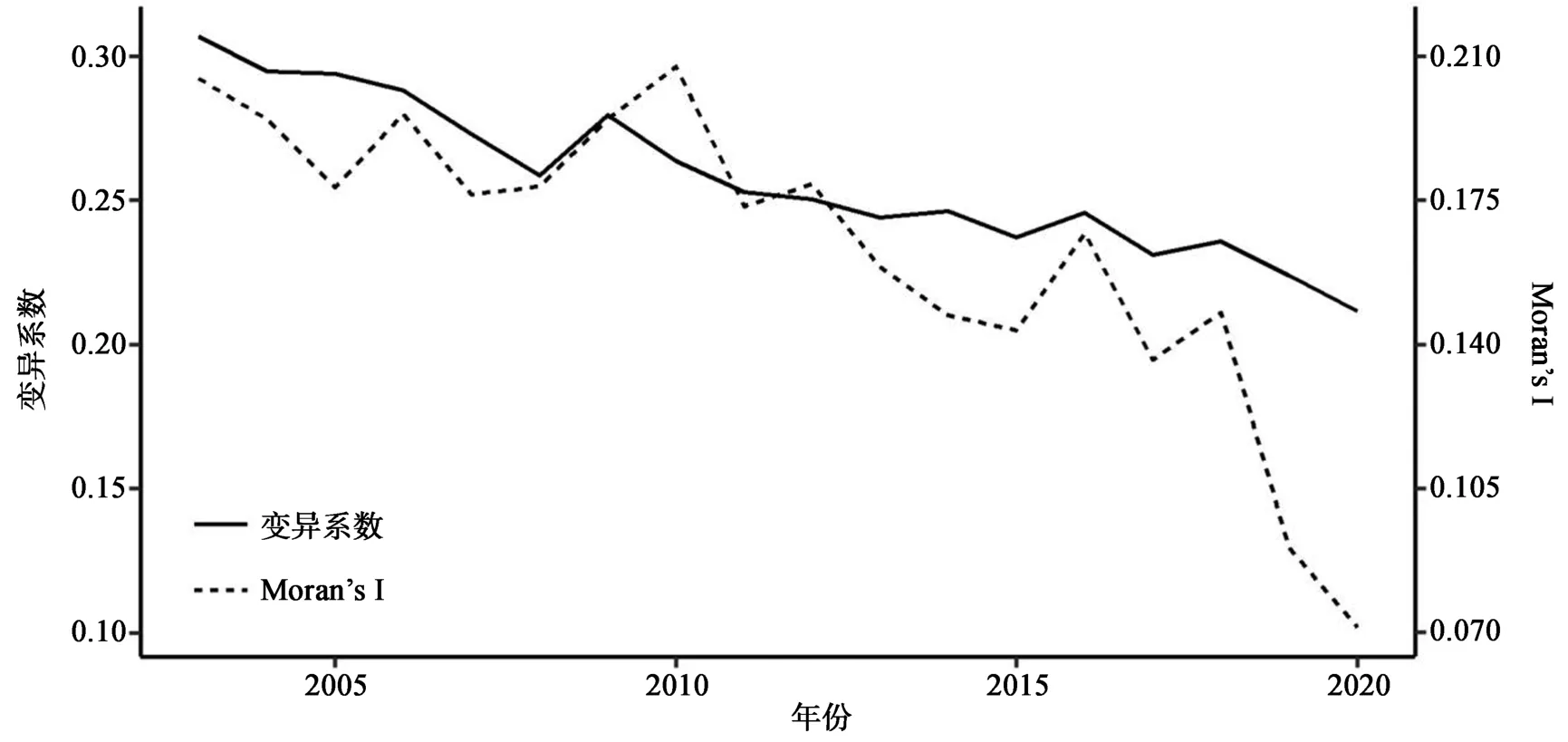
图2 长江经济带农业绿色发展水平的空间相关性和收敛情况(2003-2020)

图3和图4 分别给出了2003 年和2020 年长江经济带城市之间的农业绿色发展水平的Moran散点图,即城市农业绿色发展水平对其空间滞后的散点图。①See Luc Anselin, Spatial Econometrics: Methods and Models, Springer, 2013, p.1-3.其中,空间滞后农业绿色发展水平等于邻近地区农业绿色发展水平的加权平均值。 在所研究的时间段,初期(2003 年)和末期(2020 年)的Moran 散点图都呈现出正的空间自相关,也就是说农业绿色发展水平较高的城市倾向于集中在一起,而农业绿色发展水平较低的城市也倾向于集中在一起。 如果对比2003 年和2020 年的Moran散点图,可以发现2020 年的Moran 散点图呈现出更强的空间正相关性,因为在2020 年的Moran 散点图中,位于第二和第四象限的城市数量比2003 年减少了,且这些城市的散点更贴近所在象限的边缘,即存在向第一和第三象限靠拢的趋势。

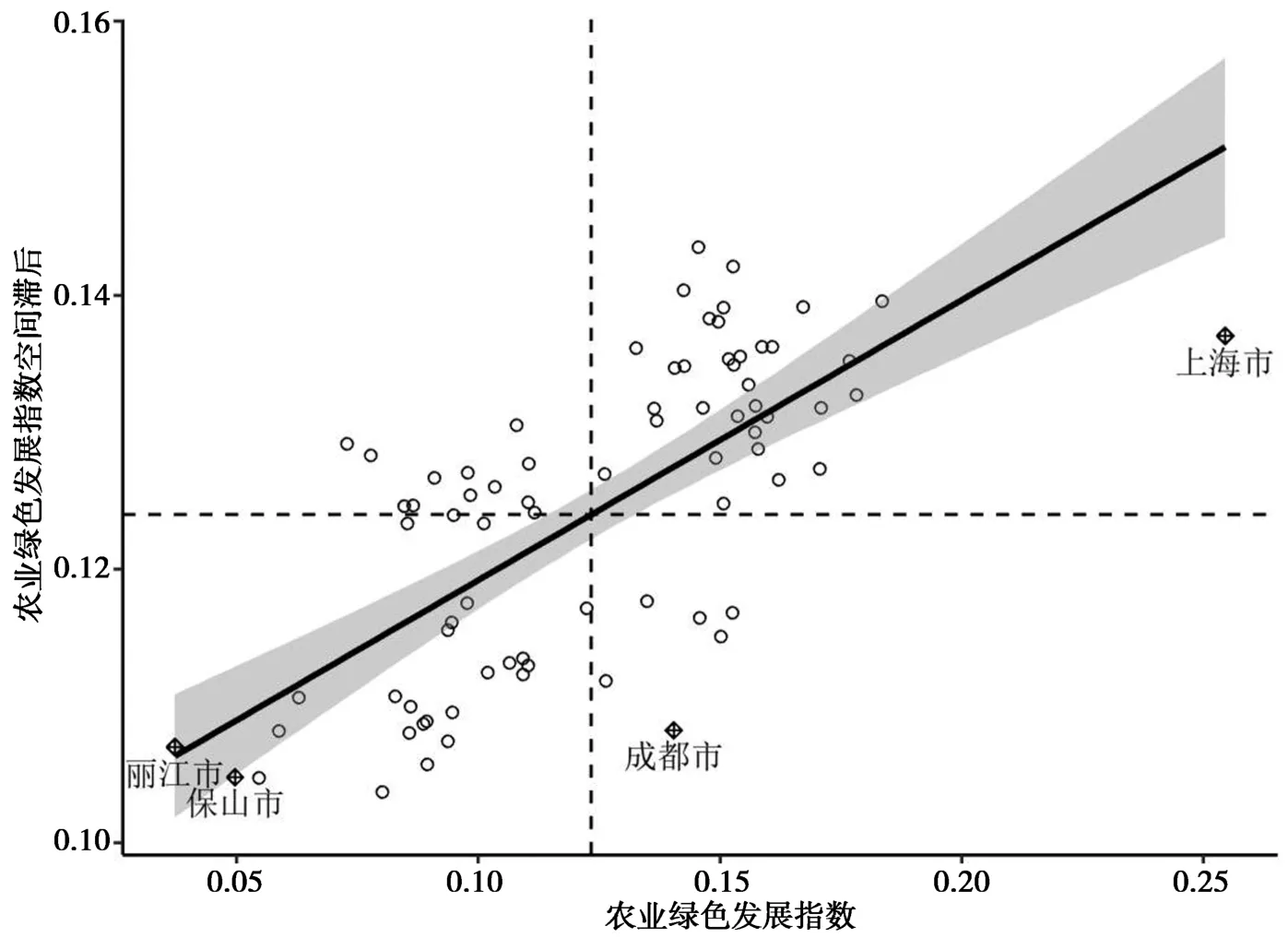
图3 长江经济带农业绿色发展指数Moran 散点图(2003 年)

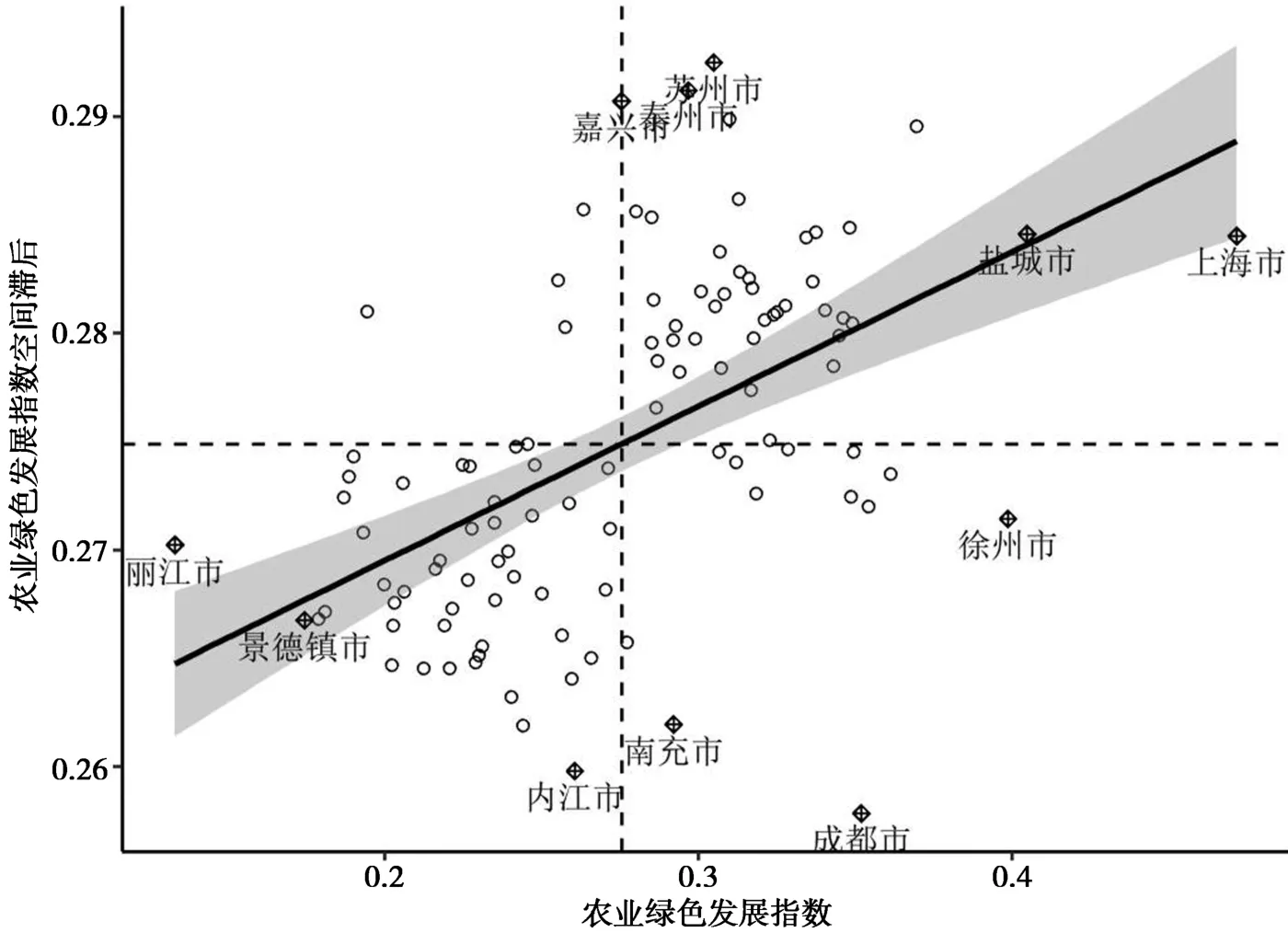
图4 长江经济带农业绿色发展指数Moran 散点图(2020 年)

图2 所反映的总体空间相关性的减弱和图3、图4 反映出的局部空间相关性增强之间并不矛盾。 也可以说,正是由于局部相关性的增强,在长江经济带形成了更多更小的聚类,从而使得总体的空间相关性减弱了。

(四) β 绝对收敛和空间相关性

从以上的分析中可以发现,在长江经济带中,城市之间的农业绿色发展水平存在着空间上的相关性。 采用变异系数来衡量长江经济带各城市的农业绿色发展水平是否收敛则无法考虑这种空间效应。

表3 中给出了β绝对收敛的检验结果。 在实证分析中,分别设定了2003-2010 年、2003-2015年和2003-2020 年三个不同的时间段,分析β绝对收敛随时间跨度的变化。 从各模型的回归结果来看,时间跨度越长,β绝对收敛系数的绝对值越大。 也就是说,在长江经济带,各城市农业绿色发展水平之间的收敛程度随着时间的推移在不断地强化,而没有减弱。

对比OLS 和不同的空间效应模型,可以发现加入不同的空间效应并不会对绝对收敛系数的显著性和符号产生影响。 如果时间跨度较短(2003-2010 年和2003-2015 年),SAR、SAC 和SDM 模型中的空间滞后项系数ρ均不显著。 只有在完整的时间跨度上(即2003-2020 年),ρ才是显著的,并且符号为正,表示存在正的空间溢出效应,这个结果和图3、图4 反映出的正向局部空间自相关是一致的。

(五) β 条件收敛和空间相关性

绝对收敛和条件收敛本质上是不同的模型。 除了条件收敛模型中需要加入更多的控制变量以外,绝对收敛和条件收敛模型的差别还在于前者使用的是一个截面数据,后者使用的是面板数据。利用面板数据可以更好地控制各地级市的个体效应。 同时在条件收敛模型中加入更多的解释变量也有助于更好的控制遗漏变量问题。

在条件收敛的实证分析中,除了对全样本进行回归之外,以10 年作为一个时间窗口,分别构建了8 个连续的子样本(具体参见表4-6 中的第一列)并分别进行回归。 这样可以更加清楚地审视长江经济带城市间农业绿色发展水平的收敛情况和空间相关性。

表4 分时间段的SAR 模型回归结果

表4-6 分别给出了分时间段的SAR、SAC 和SDM 模型估计结果,所有模型均采用了固定效应模型的设定,估计方法采用的是拟极大似然估计。①See Federico Belotti, Gordon Hughes & Andrea Piano Mortari, Spatial Panel-Data Models Using Stata, 17 The Stata Journal 139, 139-180(2017).根据AIC 和BIC 的检验结果,SAR 要优于SAC和SDM。 因此后续的分析主要是依赖于表5 的估计结果。

表5 分时间段的SAC 模型回归结果

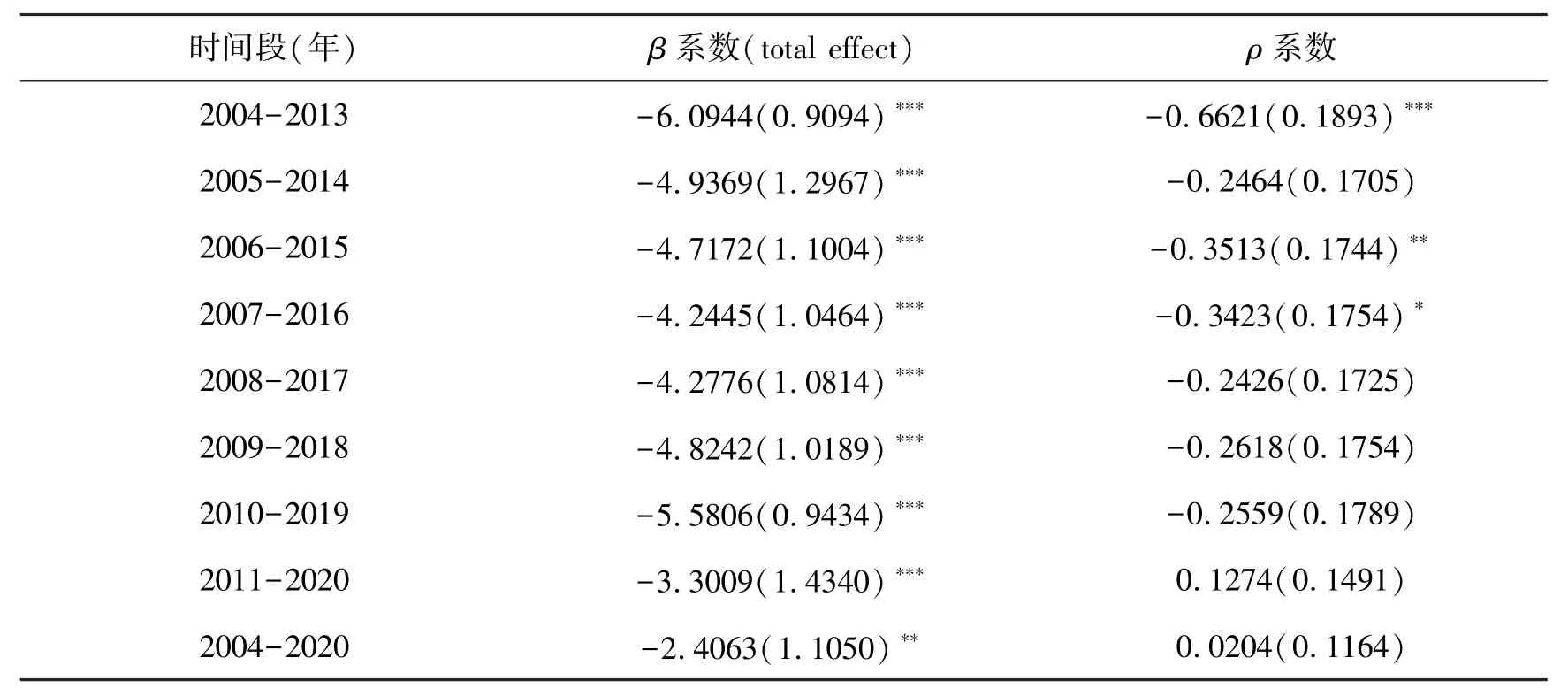
表6 分时间段的SDM 模型回归结果

可以发现,在不同的模型和不同的时间段,相对收敛系数都是显著的。 也就是说,即使在控制了固定效应和其他的解释变量之后,长江经济带中各城市农业绿色发展水平之间的收敛也是存在的。 空间相关系数ρ的估计值在不同的时间段有着较大的差异,但均是显著的。 这表明,长江经济带城市间的农业绿色发展水平所展现出的收敛性并不取决于起始时间,其结果是稳健的。

在条件收敛模型中,空间滞后效应的系数估计值和绝对收敛模型有显著的差别。 绝对收敛模型和Moran 散点图的分析结果都显示,长江经济带城市间的农业绿色发展水平存在着正的空间相关性,也就是正的空间滞后效应系数。 然而,在表3 中,却存在大量的空间滞后效应系数为负的情况,并且系数还是显著的。 从系数估计的结果来解释,负的ρ表示农业绿色发展水平高的地区被农业绿色发展水平低的地区所包围,反之亦然,农业绿色发展水平低的地区被农业绿色发展水平高的地区所包围。 但可以发现,随着时间的推移,ρ的绝对值在不断减小,并且从统计上来看越来越不显著了。 在全样本中空间滞后效应的系数也不显著。

四、讨论和结论

长江经济带要坚持“生态优先、绿色发展”,重中之重是在区域内协同推动农业绿色发展水平的不断提升。 本文重新构建了衡量农业绿色发展水平的指标体系和测算方法,利用2003-2020 年间的地级市数据对长江经济带农业绿色发展水平进行了测度,并分别利用Dagum 基尼系数、Moran' s I指数、Moran 散点图、绝对收敛和相对收敛回归模型等方法对长江经济带农业绿色发展水平的时空变化进行了全面的描述。

分析结果显示,长江经济带总体的农业绿色发展水平在不断提高,并且在初期农业绿色发展水平低的城市具有更快的增长速度,因此出现了城市间农业绿色发展水平的收敛。 将长江经济带划分为上游、中游和下游三个区域进行分析,可以发现区域间的农业绿色发展水平差异逐渐消失,区域内差异成为长江经济带农业绿色发展水平差异的主要来源。 同时,也可以发现,随着长江经济带农业绿色发展整体水平的不断提升,城市间农业绿色发展的相互影响在逐渐消失。 换言之,长江经济带中还未形成一个对全域农业绿色发展具有带动性的中心城市。 但在局部地区,部分城市农业绿色发展对其周边城市的农业绿色发展具有一定的拉动作用,这可能是由农业产业链条较短、空间辐射能力不强导致的。

随着长江经济带城市间的农业绿色发展水平差异逐渐缩小,且总体水平不断提升,农业绿色发展水平提升的速度将会不断下降。 因此,在未来,提升长江经济带农业绿色发展水平的难度将会变得更大。 要使长江经济带农业绿色水平进一步提升,一方面,需要增强城市自身的农业绿色发展动能,依靠内生动力提高本城市的农业绿色发展水平,从而对周围城市的农业绿色发展形成带动作用;另一方面,更需要加强小区域范围内城市间农业绿色发展的相互协作。