装配式建筑多空间的鲁棒性协同调度研究

汪和平,朱睿芳

(安徽工业大学 管理科学与工程学院,安徽 马鞍山 243000)

随着城镇化步伐的加快,建筑行业已成为国民经济建设的重要领域之一.近几年,在国家的政策扶持下,速度快、质量好、既节能又环保的装配式建设技术得到大力发展.2020 年,住建部等13个政府部门提出了《关于推动智能建造与建筑工业化协同发展的指导意见》,指出“要以大力发展装配式建筑为重点”[1].目前,装配式建筑施工过程基本可划分为生产、运输、现场装配环节,而这些空间的建设资源调度问题不仅具有异地域,非同步的特点,而且各个空间之间又相互制约,从而导致装配式建筑整体更易受到来自不同空间因素的影响[2],使得建筑项目普遍出现低收益、超时、超预算的局面[3].另外,各个空间具有工序复杂,资源种类、数量繁多,环境复杂等特点,使得项目的不确定性因素显著增加.因此,若能综合上述问题对装配式建筑多维空间进行合理的项目施工调度,则可以使得项目的进度计划不仅拥有工期短、成本低的优点,还能具有更强的抗干扰能力.

相比较单一的作业空间,多空间之间具有异质性,非同步性,异地域性以及空间之间相关联性的特点[3].因此,多空间的项目资源调度问题解决起来要比单一空间更加复杂.目前,国内外已经有很多学者就装配式建筑多维空间一体化的项目资源调度问题进行了深入研究.比如,Chen[4]等考虑了装配式建筑施工现场和场外制造空间的资源调度问题,以协同调度机制为重点,构建了多个构件厂与安装施工现场的静态调度模型和动态调度模型,并采用模拟退火算法(SA)解决了考虑风险延迟的调度优化问题.杨怡莹[5]将装配式建筑的多维空间划分为装配空间和生产运输空间,考虑生产运输空间对装配空间调度的影响,构建以装配空间最小成本为目标的双层规划模型,并采用嵌套式遗传算法进行求解.Yu[6]以装配式建筑的生产、运输和装配多环节的资源问题为研究对象,详细分析了装配式建筑各环节之间的约束条件,提出在建设项目资源调度优化中引入径向基函数(RBF)模糊逻辑神经网络算法来解决问题.于淼[7]等考虑了装配式建筑多空间协同调度,构建了在装配空间工期最短情况下,生产空间工期最短的多模式资源调度模型,并采用 CS 算法来解决问题.

目前大部分项目调度都是基于一个准确的时间而忽略了其他因素的影响.但在项目的实际执行过程中,会存在各种不确定性因素,比如,资源短缺,机器故障,气候变化等.此时,若继续按照原计划执行,就无法保障项目的稳定性[8].李雪[9]等考虑了不确定环境对多目标项目调度的影响,构建了以项目工期、成本最小化,鲁棒值最大化为目标的项目调度模型,并将模型划分成三个子模型,分析各目标的权衡关系,最后采用 NSGA-II 算法来解决该问题.Wang[10]等基于多模式资源限制的项目调度(MRCPSP)和鲁棒性调度理论对装配式建筑的施工进度进行优化,构建了具有最短工期、最大鲁棒值的多目标多模式资源约束项目调度模型,并且利用 NSGA-II 算法对问题进行求解.崔南方[11]等同时考虑了完工鲁棒性和计划鲁棒性构建了双目标鲁棒性项目调度模型,并对问题采用双阶段算法进行求解.Jing[12]引入了时间鲁棒性和容量鲁棒性的鲁棒指标来评估调度模型的稳定性,并提出了一种基于遗传算法和分布估计算法的多阶段鲁棒调度算法(robust hGMEDA)对活动完成时间不确定的调度问题进行求解.基于此,为了确保施工能够正常稳定地进行,管理者会更希望制定一个具有鲁棒性、抗干扰性强的进度计划.

鉴于以上分析,装配式建筑研究多集中在单一空间和确定环境下,而不确定性环境下的多空间协同调度的研究较少.因此,结合实际,本文考虑不确定因素对项目的影响,构建了以现场装配空间为主导,生产、运输空间协同的鲁棒性调度模型,为有效解决多空间协同调度的问题,使用带有精英策略的非支配排序遗传算法(NSGA-II)对模型进行求解,以此为装配式建筑安装施工方或者类似行业提供有价值的管理思路.

1 问题描述

在本文的研究中,将装配式建筑的建造过程简化为装配空间、运输空间、生产空间的联合,运用交货时间窗的方式[13]来构建调度模型.以装配式建筑的一个标准层为例,形成关键调度模型示意图,如图1所示,交货时间窗设为(ejk,ljk).

图1 关键调度模型示意图Figure 1 Schematic diagram of key scheduling model

在调度模型中,生产空间有i个项目,运输空间有j有个项目,装配空间有k道工序.以多维作业空间为y轴,以工作时间为x轴,建立了生产、运输空间与装配空间之间的约束关系坐标系.对于该问题,需要确定装配空间各个工序的开始时间,提前对生产、运输空间下达指令.在生产空间,生产单元按不同类型的构件分为i个项目;在运输空间,运输单元按不同类型的构件分为j个工作,在运输过程中,需要将生产空间的i类构件运输至施工现场进行装配,并让车辆返回.在装配空间,装配单元按照施工工艺划分为k道工序,i类构件抵达施工现场的时间应在交货时间窗(ejk,ljk)内,否则将会由于提前完成而产生存储成本.

2 鲁棒性指标

通常鲁棒性指标是指用来衡量项目进度计划抵抗干扰的能力.Vonder[14]等将项目调度鲁棒性分为两种:解鲁棒性,以项目的持续时间来判断;质鲁棒性,以计划与实际进度之间的偏差来衡量.而现有的资料介绍解鲁棒性的衡量方法主要有3种形式:基于活动时差的、基于活动开始时间偏差的以及活动参数不确定条件下的鲁棒性指标.就目前而言,由于基于活动时差的鲁棒性指标不需要考虑不确定因素的信息,以及不依赖于模拟仿真等优点,现成为衡量解鲁棒性的主要方式[15].该鲁棒性指标早期以自由时差之和的形式来表示解的鲁棒性,其中,鲁棒值越大,施工项目的稳定性就会越强.而在实际施工过程中,原自由时差之和的方式已不合适,张静文[16]等在研究中使用自由时差函数与紧后工作数量乘积的方式作为鲁棒性指标的评价标准,并用案例证明了其结果的合理性.而连静[17]在此基础上,考虑了工作性质的差异以及不同资源量的影响,提出以工序所占用各种资源的比例和来表示各工序对项目稳定性的影响系数,所描述的鲁棒性指标具体公式如下,其中,式(1)中的λig表示在i活动中,所有资源g占该类资源总数的比例之和;式(2)是对i活动自由时差的化简,Δi为i活动的自由时差,Li为i活动的工期,为保证式(3)中的a是整数,令自由时差与工期的比值向上取整;式(3)是鲁棒性指标的计算公式,S(i)为i活动紧后工序个数.

(1)

(2)

(3)

3 数学建模

本文参数符号如下:

参数参数含义i∈(1,2,…m)生产阶段的第j种构件j∈(1,2,…n)运输阶段的第j道工作k∈(1,2,…u)装配阶段的第k道工序Rg资源g的可用量rg资源g的消耗量λig第i类构件生产中资源g的占比之和λjg第j道运输工作中资源g的占比之和λkg第k道装配工序中资源g的占比之和Cg各个资源的单位成本

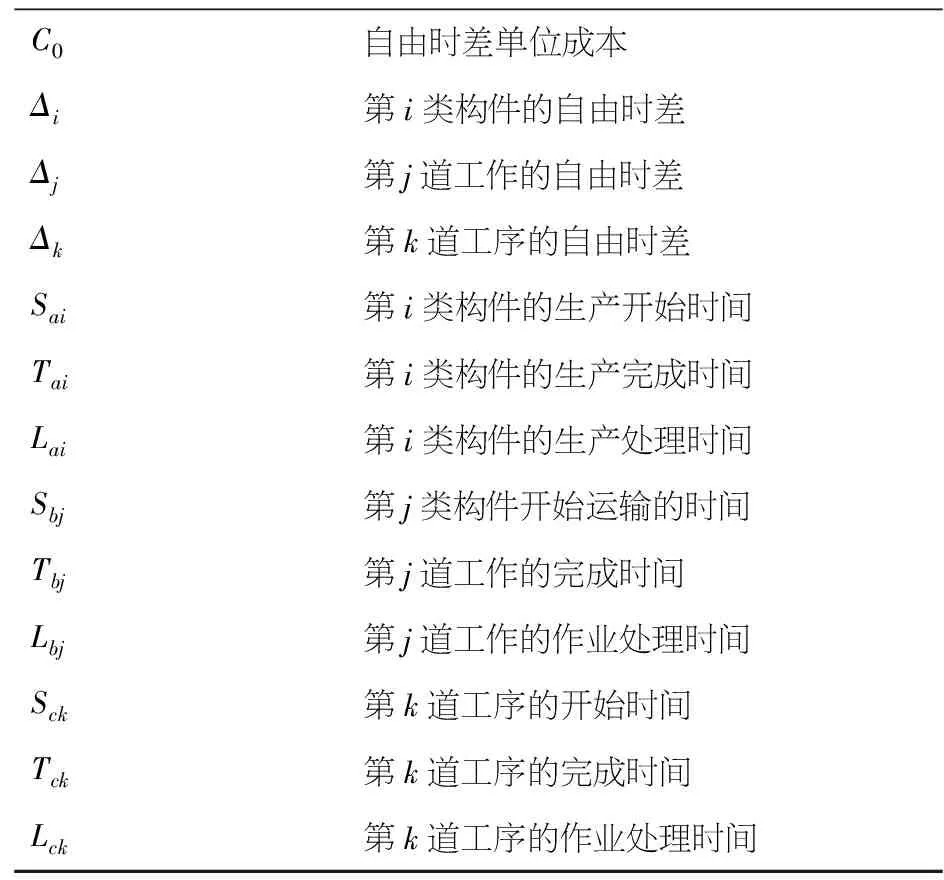
C0自由时差单位成本Δi第i类构件的自由时差Δj第j道工作的自由时差Δk第k道工序的自由时差Sai第i类构件的生产开始时间Tai第i类构件的生产完成时间Lai第i类构件的生产处理时间Sbj第j类构件开始运输的时间Tbj第j道工作的完成时间Lbj第j道工作的作业处理时间Sck第k道工序的开始时间Tck第k道工序的完成时间Lck第k道工序的作业处理时间

3.1 生产空间模型

第i类构件在生产空间进行生产,现以最小生产工期,最小生产资源及管理成本,以及最大鲁棒性作为目标进行优化,目标函数如下所示:

MinTi

(4)

(5)

MaxRM1

(6)

生产空间满足下列约束条件:

(7)

(8)

(9)

(10)

式(7)为资源约束,表示在生产空间所有正在进行的工作中,资源g的总消耗量在任何时间都不能超过资源g的可用量,其中At表示在任何t时刻正在进行作业的集合;式(8)表示生产空间自由时差的计算公式,其中succi为i工序的紧后所有工序集合,Sfi为i工序的紧后所有工序的开始时间;式(9)为模式约束;式(10)为决策变量约束.

3.2 运输空间模型

第i类构件生产结束后进行运输环节,现以最小运输工期,最小运输资源及管理成本,以及最大鲁棒性作为目标进行优化,目标函数如下:

MinTj

(11)

(12)

MaxRM2

(13)

运输空间满足下列约束条件:

Tai≤Sbj

(14)

(15)

(16)

式(14)为构件运输开始时间不能早于该类构件的生产完成时间;式(15)为运输空间的资源约束;式(16)运输空间自由时差的计算公式.

3.3 装配空间模型

第i类构件经运输抵达施工现场的时间要早于该类构件进行现场安装的时间,现以最小工期,最小装配资源及管理成本,以及最大现场装配空间鲁棒性作为目标进行优化.其中,α为构件提前到达所产生的单位储存成本,dj为第j个项目车辆返程及卸货所需的时间,具体目标函数如下:

MinTk

(17)

(18)

MaxRM3

(19)

装配空间满足下列约束条件:

(20)

Tbj-d≤Sck

(21)

(22)

Tk≤D

(23)

式(20)为装配空间的资源约束;式(21)表示第j个运输项目离开施工现场的时间要早于该类构件的装配时间,其中d为车辆返程的时间;式(22)同上;式(23)是项目的截止日期.

3.4 总目标函数

为方便计算分析,将上述三个空间的目标函数进行综合,形成以工期,资源及管理成本,鲁棒性为目标的多目标模型.

MinTk

(24)

MinP=P1+P2+P3

(25)

MaxQ=RM1+RM2+RM3

(26)

3.5 采用NSGA-II算法求解

Deb等[18]提出的NSGA-II算法是在NSGA的基础上加以完善的,他们提出在NSGA算法中增加快速非支配排序和精英策略,从而使得算法的收敛速度加快,更有利于处理多目标问题.

步骤1:初始化种群.本研究主要为了优化各空间各工序的开始时间,因而选择实数编码的方式作为个体染色体的基因编码,每条染色体中的每一位采用一定范围内的实数进行表示.

步骤2:适应度计算.采用目标函数值进行计算.

步骤3:快速非支配排序.对于多目标的优化问题,若假设Xi,Xj为任意的两个解,非支配关系应遵循以下原则:如果Xi的所有目标函数都比Xj更好,则Xj被支配,如果Xi的所有目标函数都比Xj更差,则Xj支配Xi.根据该原则,计算每个个体的非支配等级,寻找被支配个数为0的个体并放入到外部存档Archive集中,通过算法每次迭代所产生的非支配解,不断更新外部存档Archive集.

步骤4:拥挤度距离.现假定每个目标函数为fa(xb),a,b∈1,2,…,N.根据每个目标函数的结果,对个体按照从小到大排列,排在首位小及排在末位的个体,则将其拥挤度距离均定为无穷大,而其他所有非边界个体的拥挤度距离则根据式(27)进行运算:

(27)

其中:dab为第a个目标函数中的个体xa的拥挤度距离,fa(xb+1)为个体xb+1的第a个目标函数,famin、famax为目标函数a的极小值、极大值[19].为保证解的均匀性,本文在每个层次进行选择时,采用拥挤度距离进行计算,从计算的结果中优先淘汰掉排名最后的值,然后对剩余的解重新进行拥挤度的计算,以此类推淘汰掉较差的解.

步骤5:选择操作.根据个体的级别和拥挤度的大小,通过锦标赛选择法选取个体.先从种群中选出0.5N个个体,从中选取Pareto级别最低的个体,最后从其中选取拥挤度最大的个体.

步骤6:交叉操作.模拟二进制交叉方式,以交叉概率Pc=0.8从上个操作的新种群中选择出要参加交叉操作的父代,然后按照式(28)～(30)对每一对父代进行交叉操作,产生子代[20].

(28)

(29)

(30)

步骤7:变异操作.设变异概率Pm=0.01,从上个操作的新种群中选择参加变异操作的父代,然后按照式(31)～(32)对每一对父代进行变异操作,产生子代.

x1j(t)=x1j(t)+Δj

(31)

uj∈U(0,1),η=1

(32)

步骤8:改进精英保留策略.将Pareto等级相同的种群整个放入子代种群中,直到某个等级的个体不能全部放入.此时,按照原算法操作:对这个等级的个体,按照拥挤度,从大到小选取,直到子代种群放满为止,但是这会导致结果的分散性和随机性变强,也就是说前沿解的跳动会更加剧烈.基于此,删除拥挤度最小的点,重新计算拥挤度,如此循环,直到满足popsize.

步骤9:超过迭代次数算法终止.

3.6 多目标决策

根据上述算法进行求解,最后会得到一个Pareto最优解集.若想要获得Pareto最优解中的最优方案,则要根据决策者对多目标的偏好进行选择[21].在确定完指标体系和指标权重之后,对原始数据进行归一化处理和加权综合.其中,要提前判断原始数据是否具有同向性,若无同向性,需要对其先进行同向化处理再加权,从而使目标函数值具有可比性.计算如式(33):

(33)

(34)

4 实验设计与结果分析

本文现选择某装配式建筑的某一标准层进行装配式建筑施工.其中,每类构件在预制构件厂生产结束,通过运输到达装配现场.其中,生产空间包括12项生产项目,分别是对3种外墙,2种内墙,3种叠合板,2种叠合梁,2种异性构件(楼梯,阳台)的生产,并且基于资源投入量的不同将项目分为两种执行模式,生产空间的单代号网络图见图2,其中表1为各个空间的资源供应情况.活动名称及资源工期情况见表2;由于要对生产空间的12类构件进行配送,因此运输空间也被划分为12道,其各工序优先级关系可视为与生产空间一致,运输空间的名称及资源工期情况见表3;而装配空间主要包括18道工序,资源分为五类,分别为:吊装工,钢筋绑扎工,灌浆工,普工以及塔吊,其单代号网络图如图3所示,活动名称及资源工期情况见表4.

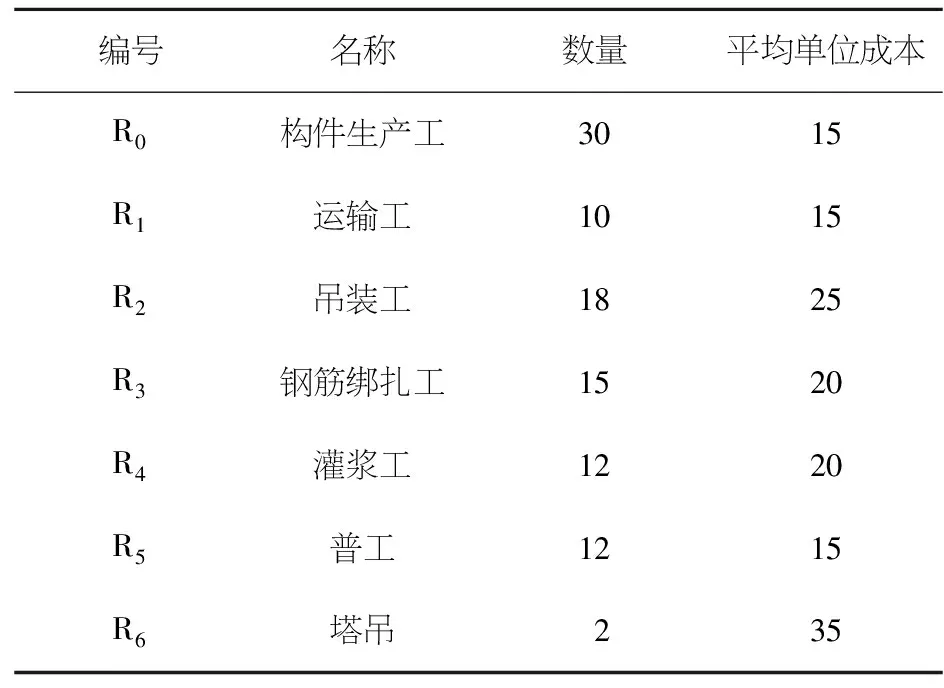
表1 资源供应Table 1 Resource supply

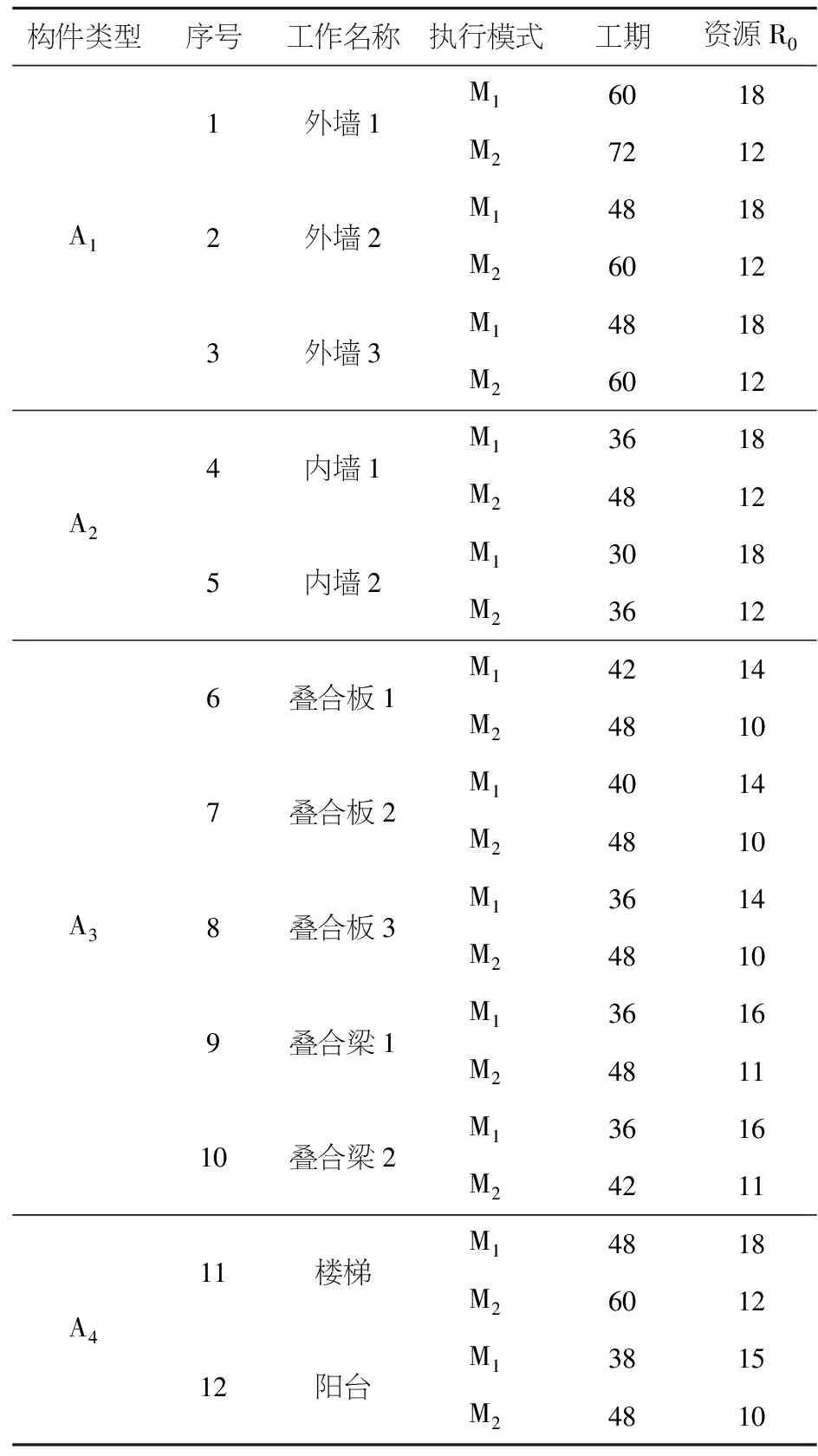
表2 生产空间资源与工期需求Table 2 Demand for production space resources and construction period

表3 运输空间资源与工期需求Table 3 Demand for transportation space resources and construction period

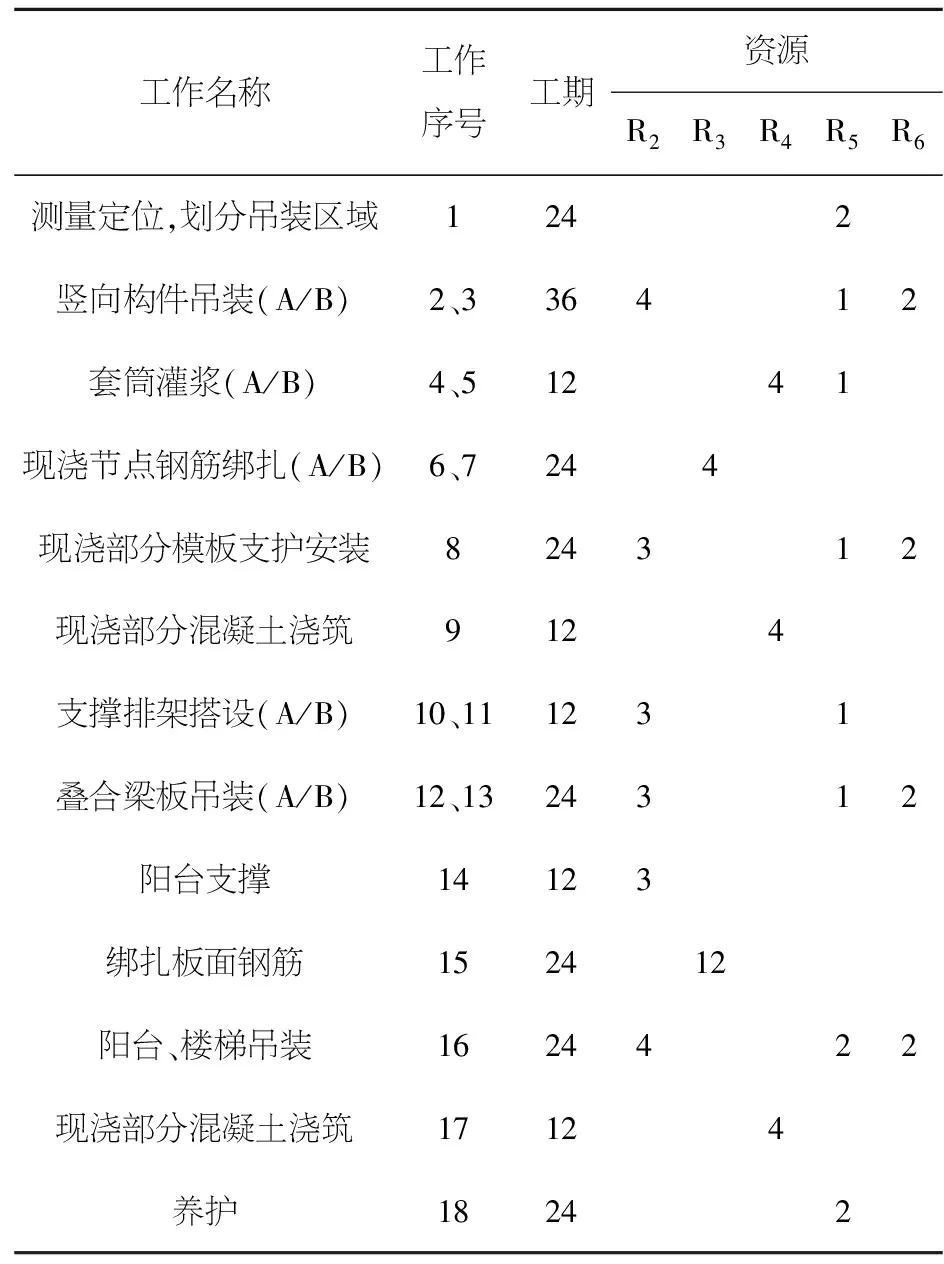
表4 装配空间资源与工期需求表Table 4 Requirements for assembly space resources and construction period

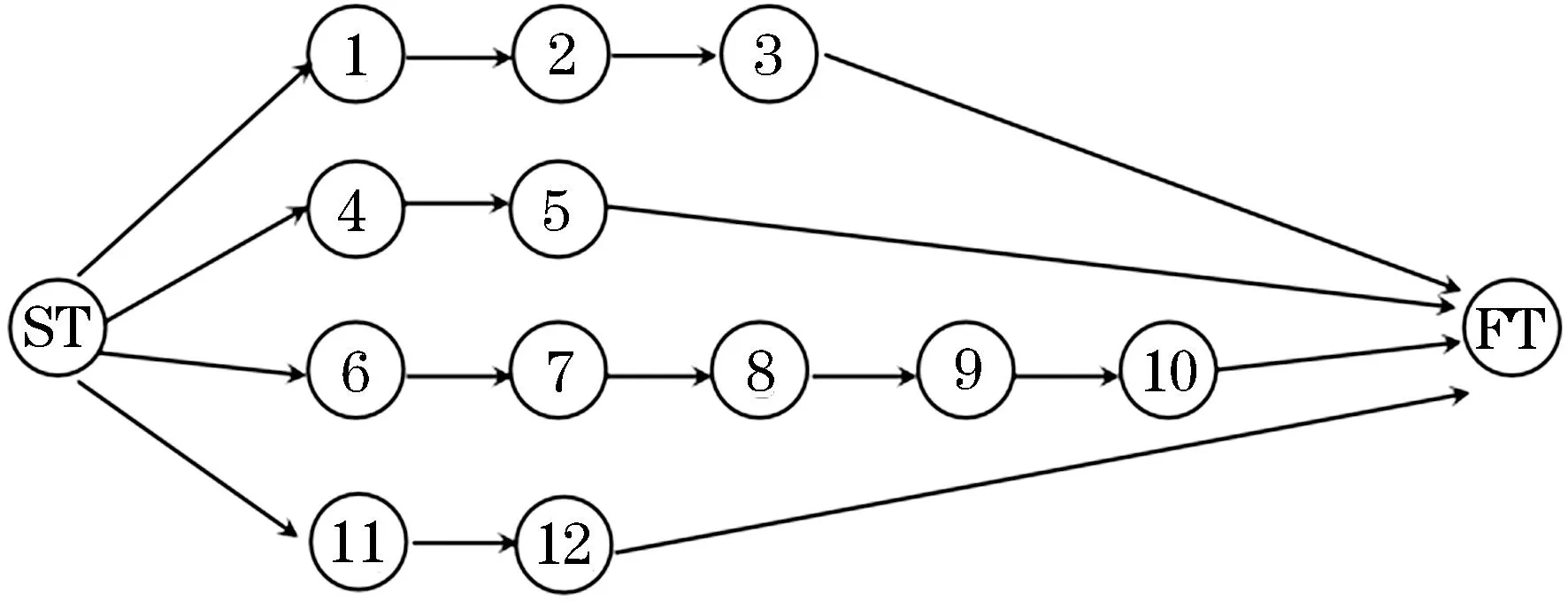
图2 生产、运输空间单代号网络图Figure 2 Production and transportation space single code network diagram

图3 装配空间单代号网络图Figure 3 Single code network diagram of installation space

根据实际情况,现规定构件装配空间的交货时间窗(ejk,ljk)所需的时间段为4,返程时间为4.提前到达所产生的单位库存成本为10,项目的截止日期设为70 d.

本文采用Matlab.R2018b对问题进行运算,设置种群个体为30,算法最大迭代次数为500.计算得到近似帕累托前沿如图4所示.从图4中可以发现,当总工期、总资源及管理成本较大时,总鲁棒值会相对较大,而当总工期、总资源及管理成本都较小时,总鲁棒值相对较小.

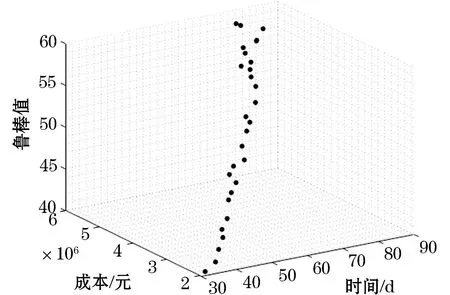
图4 近似帕累托前沿Figure 4 Approximate Pareto front

为求得令决策者满意的解,现对整体方案进行选择,由于总工期、总资源及管理成本都是越小越好,而总鲁棒值是越大越好,因此为了便于比较不同量纲的目标函数,首先对各指标进行同向化处理,并根据施工方的偏好,对各指标赋予权重.为重点体现项目的鲁棒性,现假设对总工期赋予权重w1为0.3,总资源及管理成本w2为0.3,总鲁棒值w3为0.4,根据式(32)、(33)进行计算,最终根据偏好选择出最合适的结果.见表5.

表5 方案选择

根据数据,选择综合指标最大的方案8,工期为1 017,总成本为2 354 045,总鲁棒值48.212 3.在该方案下,各个空间的最优调度结果如表6所示.此时生产空间最佳模式选择为(1,2,2,2,1,2,1,1,1,2,1,2),在该模式方案下,生产空间的最优资源调度计划如图5所示,其中(a,b,c)为(工作序号,工期,资源数量);运输空间的最优资源调度计划如图6所示,其中(a,b,c)为(工作序号,工期,资源数量);装配空间的最优资源调度计划如图7所示,其中(a,b,c)为(工作序号,工期,资源种类).可以看出,资源种类以及数量在整个工期下的分配计划,以此可为施工方寻求稳定的调度计划提供决策支持.

表6 各空间最优调度结果

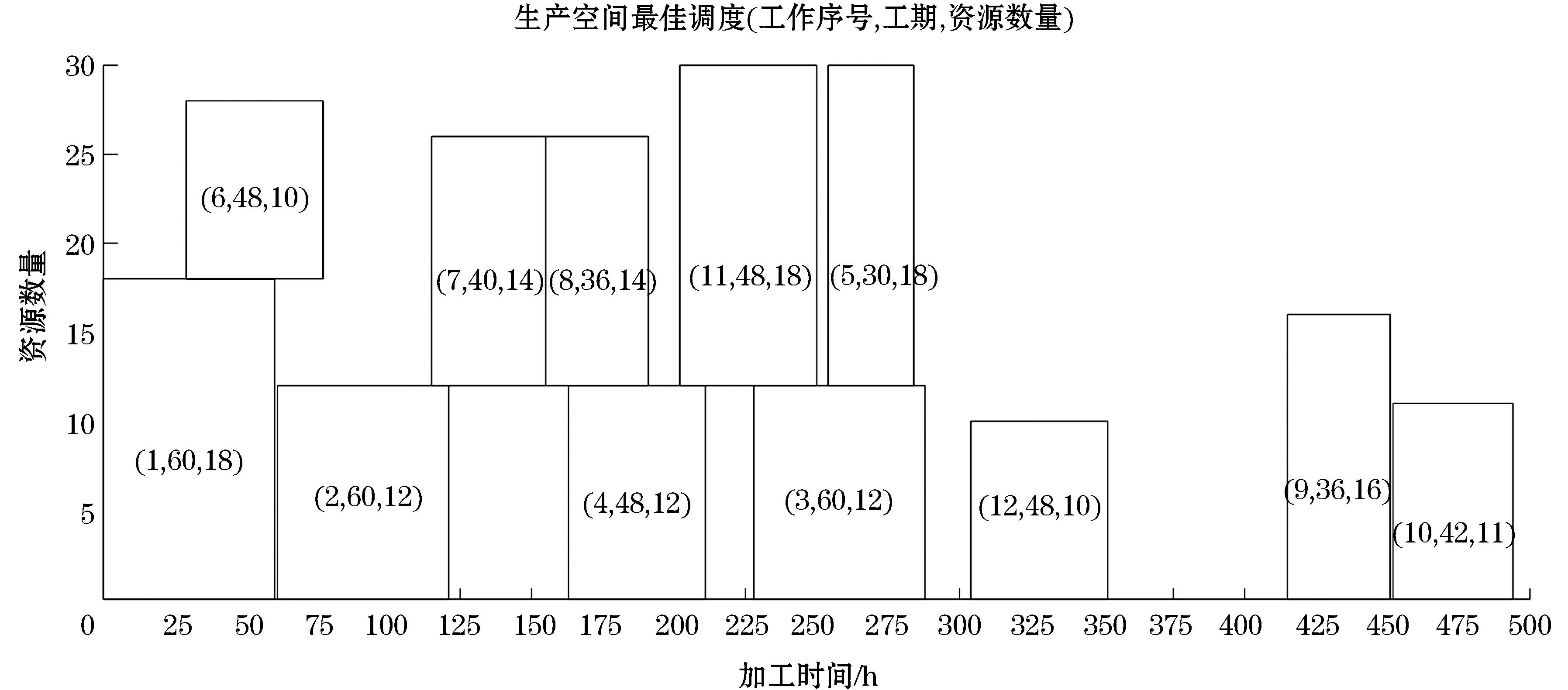
图5 生产空间最优资源调度计划图Figure 5 Production space optimal resource scheduling plan

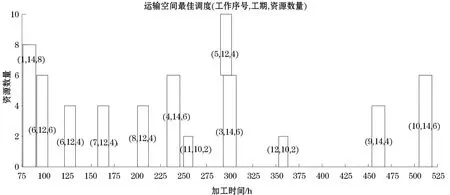
图6 运输空间最优资源调度计划图Figure 6 Transport spatial optimal resource scheduling plan

5 结 语

目前的装配式建筑协同调度研究中,往往考虑的是确定环境下的施工状态,而在实际施工过程中,不确定性因素以及资源限制会对整个项目造成不可忽视的影响.因此,本研究从装配式建筑实际出发,考虑多个空间的协同管理,构建了基于鲁棒性的装配式建筑多空间协同调度优化模型.采用带精英策略的快速非支配排序遗传算法对该模型进行求解.通过案例分析,获得了适合决策者偏好的多空间最优调度计划结果,有效解决多个空间在实际调度中面临不确定因素的问题,为装配式建筑多空间的协同调度问题提供决策帮助.