基于有限元分析的圆形深基坑开挖变形数值分析

康 健 军

(中铁十八局集团第四工程有限公司,天津 300000)

1 研究背景

圆形深基坑工程项目的变形发展及其破坏模式,与基坑在开挖过程中产生的应力场变化有着十分密切的联系.因此,为实现高质量工程施工,必须开展对圆形深基坑开挖过程中应力场、应力场演变规律等相关变形数据的研究,并借助相应数值模拟的形式实现.有限元分析方法是岩土工程领域当中常见的一种用于对数值进行分析的方法[1-3].有限元分析方法与传统设计计算方法相比,能够充分考虑到岩土工程中土体的本构模型以及土质与支护结构之间的各个应力和位移变化,从整体的角度对支护结构以及周围土体的应力进行动态模拟分析.但目前有限元分析方法并未应用到圆形深基坑开挖环节当中,因此没有相应的针对圆形深基坑开挖过程中变形数据的有限元分析方法,传统方法在实际应用过程中还会存在数值变化无法进行动态捕捉、结果与实际出入较大、具体实施困难等问题[4-6].

因此,针对上述问题,本文开展基于有限元分析的圆形深基坑开挖变形数值分析研究.

2 圆形深基坑开挖变形数值分析方法

2.1 圆形深基坑周围土体模型构建

在对圆形深基坑开挖变形数据进行分析前,首先需要构建与该基坑周围土体结构相同的模型.通常情况下,当应力的水平相对较低,或在进行圆形深基坑开挖过程中,初期阶段基坑周围的土体塑性区域相对较小.此时,根据分析需要,可忽略土体的塑性变形数值,认为土体本身具有一定的弹性性状即可[7].但在实际运行深基坑开挖时,随着开挖不断向周围和深部扩张,塑性区域也会逐渐扩张,并形成一整片塑性区域,此时需要将土体本身的塑性变形因素考虑.由于圆形深基坑周围软土结构在屈服后期抗剪强度以及摩擦角度仍然处于较小的情况,测量相对困难.因此,可将圆形深基坑周围土体看做理想塑性材料进行分析.在开挖过程中,可将开挖操作划分为多个不同开挖动作构成的活动[8-10].开挖过程中会造成在开挖线上各个点的应力得到释放,并产生相应的应力场变化和土体变形.因此,为了保证构建的模型能够更加准确地模拟具体开挖施工的工况,本文在设计模型时采用增量形式的构建关系.

引入弹塑性模型构建方法,将本文模型构建在考虑静力压力和屈服准则的基础上,得到该模型的屈服准则为:

(1)

其中:F(x,y)为屈服准则标准参数;α、k为屈服准则材料常数;x为土体在应力状态下的第一不变量;y为土体在应力状态下的偏应力张量第二不变量.按照水平方向上的应变条件,得到圆形深基坑开挖过程中土体的应变和变形条件,土体的应变可表示为:

(2)

其中:α为土体应变数值;θ为土体残余摩擦角.

土体的变形条件可表示为:

(3)

其中:k为土体变形条件数值;c为土体残余剪强度.

通过对模型进行反复的加载,土体模型最终会表现出一定的硬化,通过对该模型的硬化性质进行分析,为后续圆形深基坑开挖白晓宁数值分析提供依据.

2.2 圆形深基坑开挖接触面与支护结构模拟

在进行圆形深基坑开挖过程中,支护桩结构、地下连接墙结构等均会与土体相互接触,从而间接使土体具有特殊的变形性质.由于混凝土材料与土的变形模拟量之间的性质存在着较大的差异,因此各类结构物与土体的接触面上都需要额外进行模拟[11].综合上述分析,本文采用改进后的结构平面为单元的方法,利用该单元表示土体中与各类结构物相连接的部分.假设该单元的承受水平方向上的剪应力为γ,垂直方向上的法向应力为σ,则接触面的应力与变形关系之间对应的局部坐标(c,d)可以改写成:

(4)

其中:K为土体模型接触面单元上的刚度;Δuc为土体模型接触面单元两侧对应的相对水平方向位移;Δud为土体模型接触面单元两侧对应的相对垂直方向位移.

圆形深基坑支护结构中的桩和地下连续墙等结构均可通过引入剪切变形的梁单元进行模拟;支护结构中的锚杆或支撑等均可通过杆单元进行模拟[12].由于桩和地下连接墙结构已经是完整的结构,因此在对圆形深基坑开挖过程中的土体进行变形分析时,可将实际释放的荷载引入到桩单元和土体共同组成的组合结构模型当中.在圆形深基坑开挖时释放的荷载对土体连接的锚杆、桩等结构均起到一定的作用.圆形深基坑开挖是一个循序渐进的过程,因此需要利用本文上述构建的模型对开挖的全过程进行模拟,并充分考虑各结构之间的共同作用.

对于土体周围的支护排桩和锚杆应当根据实际需要,采用连续性的方式,将其转化为等效的抗弯刚度以及等效杆的抗拉刚度,从而方便对圆形深基坑开挖过程中周围受到影响的土体变形进行分析.

再从整体分析角度来看,开挖阶段锚杆的刚度并不是特定不变的数值,会随着平面位置的改变发生变化[13].因此,根据这一点,假设开挖结果会向锚结构和支撑结构周围同时施加单位应力,并对各结构的柔度进行计算,而刚度则可看作是柔性的倒数,即刚度T=1/δ.由于在进行圆形深基坑开挖工程时,框架周围的点会产生不同的位移,因此其刚度同样会发生不同的变化.根据刚度的变化特点,直线变长上的中间点位移越大,对应的刚度系数越小[14].因此,根据上述特点,为了方便后续分析,本文将对土体周围的支撑杆件单元考虑,结合材料力学分析方法,对其刚度系数进行计算,得出式(5):

(5)

其中:E为土体的弹性模量;A为圆形深基坑支护结构的横截面积;SL为土体的坍落度.通过式(5),完成对圆形深基坑开挖接触面与支护结构的模拟.

2.3 圆形深基坑开挖过程模拟计算

在实际圆形深基坑开挖过程中,开挖前土体的变形数值为0,将开挖的工作面作为应力自由面.在进行开挖工作前,其自由面上各点均处于相对平衡的状态.在开挖过程中,被挖去的土体单元作用力会逐渐消失,造成整个土体失去原有的平衡状态,进而造成圆形深基坑结构出现变形,并且伴随着应力场的改变[15].针对圆形深基坑开挖过程进行模拟,可采用对各阶段开挖荷载的计算方式实现.将圆形深基坑开挖过程模拟如下:

(6)

其中:F为圆形深基坑开挖过程中开挖边界上的应力大小;n为单元数;B为土体变形量;σ为土体单元的应力大小.

将式(6)计算得出的开挖边界上的应力作为土体的外力荷载,将其引入到本文上述模型和总的相应位置上,可以更加准确的模拟出圆形深基坑开挖过程中边界上的变形效果,并通过反转应力释放方法,根据其变现位移量,确定在开挖后基坑产生的变形位移量.

为进一步贴近真实开挖过程中的基坑的变化情况,在完成对土体的开挖后将基坑的体系刚度数值适当降低,本文采用控制单元的方式,将开挖后掉落的土体单元取一个极小的数值,例如10-6.进行最小值处理后,被挖去的土体单元中,结点会逐渐成为孤立结点,此时这些结点在后续有限元分析过程中不会对最终的变形结果造成影响,确保本文提出的变形数据分析方法的准确性.

2.4 基于有限元分析的开挖过程变形分析

图1为基坑内外破坏区域的大小及具体分布范围.产生这种现象的原因是与墙角相互连接的土体塑性区域内的土体受到了破坏作用力,出现松动现象,并且整体呈现出隆起的状态.同时,与土体单元相连接的破坏区域发生改变是圆形深基坑底部隆起失去稳定性的前兆特征.

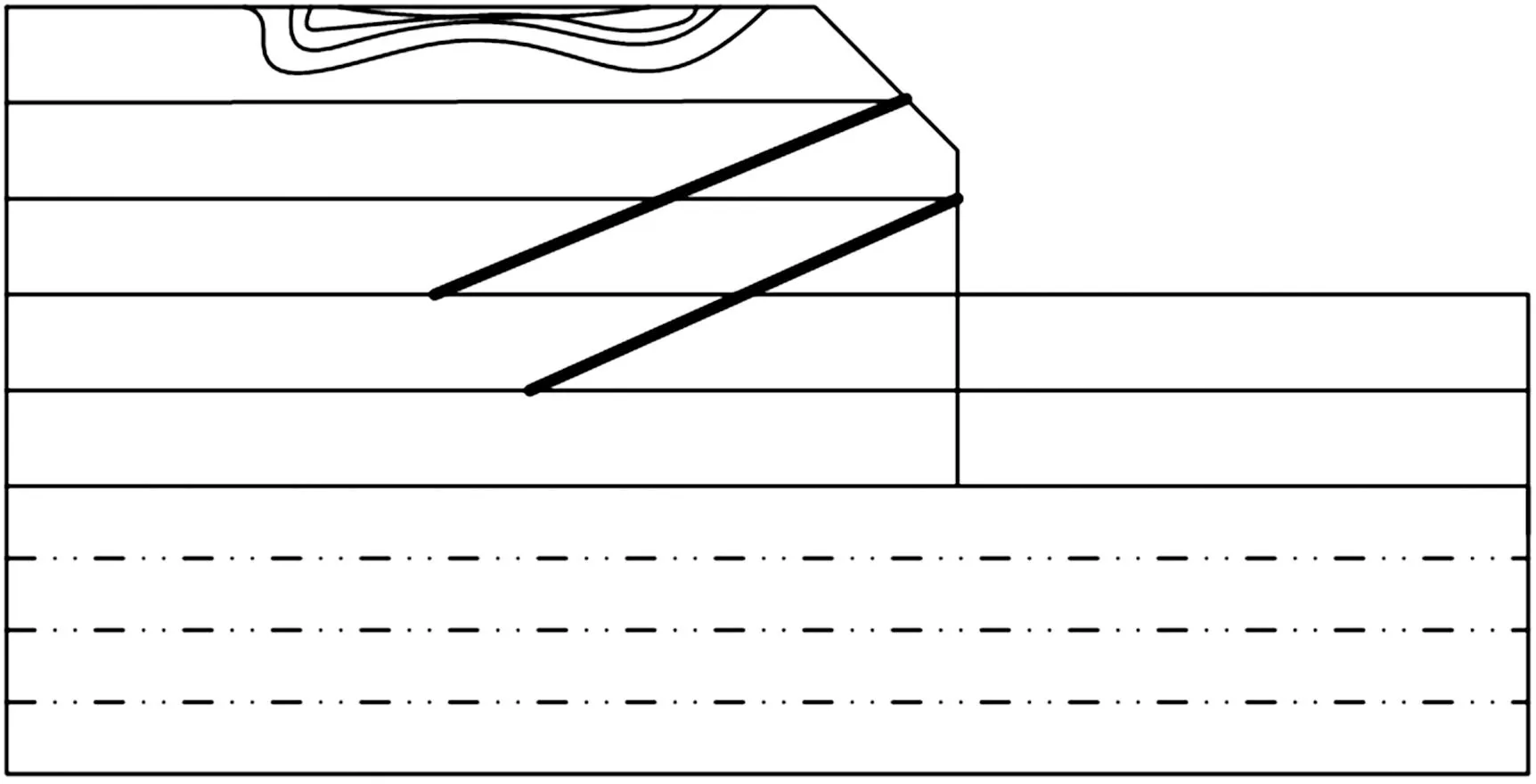
图1 基坑内外破坏区域的大小及具体分布范围Figure 1 Internal and external damage area and specific distribution range of foundation pit

结合有限元分析方法,对这一现象进行变化数值分析得出,在进行圆形深基坑开挖过程中,产生的直接结果是造成周围土体发生隆起,并产生基坑内部的土体单元受到支护结构的作用出现压力不平衡的问题,因此进一步造成支护结构向基坑内部的侧向变形达到全新的平衡状态[16-17].在这种平衡状态下,支护结构的外侧土压力会逐渐向着主动土压力的方向发展,而内侧的土压力会逐渐向着被动土压力的方向发展.由于基坑中的支护结构在不同位置上的变形程度均不相同,因此土压力的发展及分布不会按照规范的线性方式进行,以此完成对开挖过程变形数值分析.

3 实验论证分析

3.1 实验条件

本文选择某地区正在施工的圆形深基坑开挖建设项目作为实验背景,分别利用本文提出的基于有限元的数值分析方法与传统方法对该项目中的基坑开挖变形情况进行分析.该基坑结构的开挖深度为18.65 m,由于该地区地质条件较为复杂,因此在综合考虑其工程场地地质资料后,开展对实验对比.为方便对两种分析方法进行比较,本文采用基坑土体单元的水平方向和数值方向上的变形量作为对比数据,比较通过两种分析方法分析出的基坑开挖形变结果,并将其与该工程在完成后的实际基坑变化进行对比,验证两种方法的准确性.

3.2 实验结果与分析

根据上述实验条件,完成对比实验,分析结果见表1.

表1 两种分析方法实验结果对比Table 1 Comparison of experimental results of two analytical methods

表1中,(x,y)为圆形深基坑开挖过程中水平方向和竖直方向上的变形数值.由表1中的数据可以得出,本文分析方法得出基坑变形数据与传统分析方法得出的基坑变形数据相比,明显更加接近该工程项目中实际测量得到的数据.针对不同土质得到的数值精度不会产生差异.因此,通过实验证明,本文提出的基于有限元分析的圆形深基坑开挖变形数值分析方法得到的分析结果准确性更高,与真实数值更相符.将本文提出的分析方法应用于实际可以为施工企业提供更有利的数据支撑,并为后续基坑支护结构的建设与维护提供有力的依据.

4 结 语

本文针对圆形深基坑在进行开挖过程中其基坑结构发生变形的现象进行分析,并根据其施工需要和土体单元的具体变化特征,提出一种结合有限元分析的方法.在后续的研究中,还将利用本文提出的分析方法,对圆形深基坑开挖工程项目中涉及的应力场和塑性区域分布规律和变形机理进行深入研究,从而找出影响基坑变形的主要因素,为基坑建设施工项目提供有力的支持.