旅行商问题的DNA可视化计算模型
2023-12-20张彤彤殷志祥蒋天怿郑雅雯
张彤彤, 杨 静, 殷志祥, 蒋天怿, 郑雅雯
(1.安徽理工大学 数学与大数据学院, 安徽 淮南 232001; 2.上海工程技术大学 数理与统计学院, 上海 201620)
随着计算机技术的高速发展,在分子计算、纳米技术和生物医学等领域,传统的电子设备无法直接参与进程,而基于DNA分子的化学反应网络作为一种有效的编程语言可以在分子计算、纳米技术和生物医学等领域通过多种方式存储和处理信息[1].DNA折纸术作为化学反应网络的基本构建原理之一,目前广泛应用于生物计算、生物传感器、医药载体及信息安全等方面,取得了很大的发展[2-10].
2019年,Chao构建了一个单分子DNA导航系统,它可以对锚定在二维DNA折纸基地上的十顶点迷宫树上执行单分子平行深度优先搜索.通过单分子DNA导航器可以遍历的探索出迷宫的所有可能路径,从而找到迷宫的正确路径[11].同年,Zhang开发了DNA折纸加密技术,该技术利用M13mp18病毒支架折叠成纳米级的自组装盲文图案来进行安全通信,从而可以创建大小超过700位的密钥[12].2020年,Fan等人演示了基于可重构DNA折纸多米诺阵列的分子信息编码方式,当添加一组密钥(DNA链)时,图形数据可以在DNA折纸多米诺阵列中转换成可见的图案[13].2021年,Tang提出了构建基于DNA折纸基底的DNA分子逻辑电路的策略[14].跟传统的纳米自组装技术相对比而言,DNA折纸术具备设计简洁、操作简便易上手、组装效率高、反应速率快、实验成功率极高且实施过程并不复杂及纳米可寻址等优势,因而更容易构造出结构稳定、精度准确率高、复杂但可控的纳米结构.研究人员在分子生物技术的钻研历程中,对DNA折纸术的研究探索从一维结构晋升二维结构再深入到三维结构,意味着DNA折纸术的研究空间广阔,并且在NP完全问题的求解方面扮演着不可或缺的角色.
为降低NP-完全问题的复杂度,为旅行商问题提供更简明扼要的解决方案,本文利用DNA折纸术折出固定的长方形纳米结构作为折纸基底,将旅行商问题映射为折纸基底上的有向图,利用分子信标求得该问题的最优解.
1 旅行商问题的DNA计算模型
1.1 分子信标
分子信标(Molecular Beacon)是一种寡聚核苷酸探针,具有茎环结构和双荧光基团标记的发夹结构的分子探针,基于碱基互补配对原则(The principle of complementary base pairing)及荧光共振能量转移现象(Fluorescence Resonance Energy Transfer)设计构成[15].分子信标通常包括环状区、茎干区、荧光基团和猝灭基团四个组成部分.其作用原理为:没有靶分子时,分子信标的荧光基团和猝灭基团靠得很近,由于荧光共振能量转移原理荧光被吸收.当双链杂交体形成时,分子信标与序列完全互补的靶分子进行特异性结合,分开分子信标茎杆互补区,改变了空间构型,荧光基团和猝灭基团距离增大,荧光恢复.
1.2 杂交链式反应
早在2004年,著名学者Niles Pierce 和Robert Dirks运用DNA纳米结构实现了自组装,称为杂交链式反应(hybridization chain reaction,HCR)[16].该反应明确表示,在没有任何外部输入的前提下,DNA与底物的结合能够实现自主完成识别和信号放大的目的.杂交链式反应的反应物通常包含2个发夹DNA探针H1和H2以及引发链I.当溶液中不使用引发链I时,溶液中并未自发的发生杂交链式反应,而是2个发夹DNA探针H1和H2在溶液中稳定的共存.然而当引发链I添加进溶液时,引发链I会启动2个发夹DNA探针H1和H2触发杂交链式反应,在反应终止后一条长的双链DNA便会自组装形成.图1所示为杂交链式反应的原理图.引发链I识别方法是将第一个发夹DNA探针H1的黏性末端及其茎部(a-b部分)相结合,利用杂交链式反应,使得H1的茎环结构开启,且致使暴露出的单链H1(c-b*部分)展示出来,裸露在外;接着第二个发夹DNA探针的黏性末端及茎部(c-b*部分)被上一部分暴露外部的碱基识别并与第二个发夹DNA探针杂交,以至于第二个发夹DNA探针H2的茎环结构被其打开,从而致使暴露出的单链(a*-b*部分)又能够识辨且开启接下来的一个H1的茎部和黏性末端.
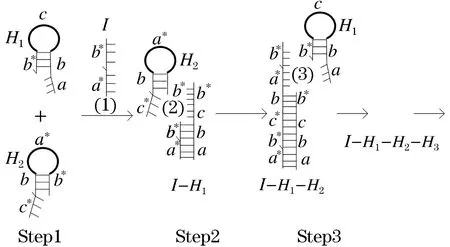
图1 杂交链式反应的原理图Figure 1 Schematic diagram of the hybrid chain reaction
上述杂交链式反应的原理可以用来说明其中的化学过程,科学研究显示杂交链式反应属于等温扩增技术,只要提供简单的控温仪器设备就可以完成该反应,大大降低了对于仪器复杂度的要求.不仅如此,还可以大幅度降低实验的成本,因为该反应不需要辅助酶的参与,具有良好的重现性.现阶段,利用该技术进行信号放大在生物医学领域得到了广泛的应用[17].
1.3 旅行商问题
旅行商问题(Traveling Salesman Problem,TSP)是一个典型的组合优化问题.TSP问题通常被描述为:一个商人要找一条通过n个城市的最短回路.即给定一系列点集V(|V|=n),在点集中从一点出发,寻找一条最短路径,该路径经过点集中的所有点,并且每个点只经过一次.对于该问题可以初步表示为:
(1)
(2)
(3)
xij∈{0,1}, ∀i,j∈V
(4)
其中:xi,j表示从节点i到节点j的路径,ci,j表示路径i→j的长度;第一个约束保证一个节点只出发一次,第二个约束保证一个节点值到达一次.由于旅行商问题可能的路径总数与城市数目n是呈指数型增长的,所以很难求得其最优解.生活中很多问题例如连锁店的货物配送路线等,都可以通过简化处理和数学建模变成TSP问题.因此对TSP问题求解方法的研究具有很重要的实际价值.
2 旅行商问题DNA算法生物实现
2.1 算法步骤
设有n个城市,一个商人从某城市出发,要经过其余的(n-1)个城市,最终回到出发的城市,共有m条可能的路线,利用DNA算法求解此商人经过的最短路径的步骤如下:
步骤1 利用DNA折纸术折叠出具有固定大小的长方形DNA纳米结构,即用其作为DNA折纸基底,也就是说二维矩形的折纸基底是大量订书钉链将环形噬菌体(M13mp18)折叠而成;
步骤2 任意两个城市之间的路径用一段亚稳态得到发夹结构的分子信标表示,在发夹结构的茎部固定猝灭基团和荧光基团,共有m条路径;
步骤3 每一座城市即顶点用分子信标表示,并且将分子信标固定在DNA折纸基底上,然后将路径映射为一个有向图,选择根节点最终将问题映射为有向树,将有向树锚定在折纸基底上;
步骤4 通过杂交链式反应,反映出经过每个点且长度最短的DNA长链,即为旅行商问题的最优解,同时可用荧光标记此链,实现该算法的可视化.
2.2 算法模型的实例分析
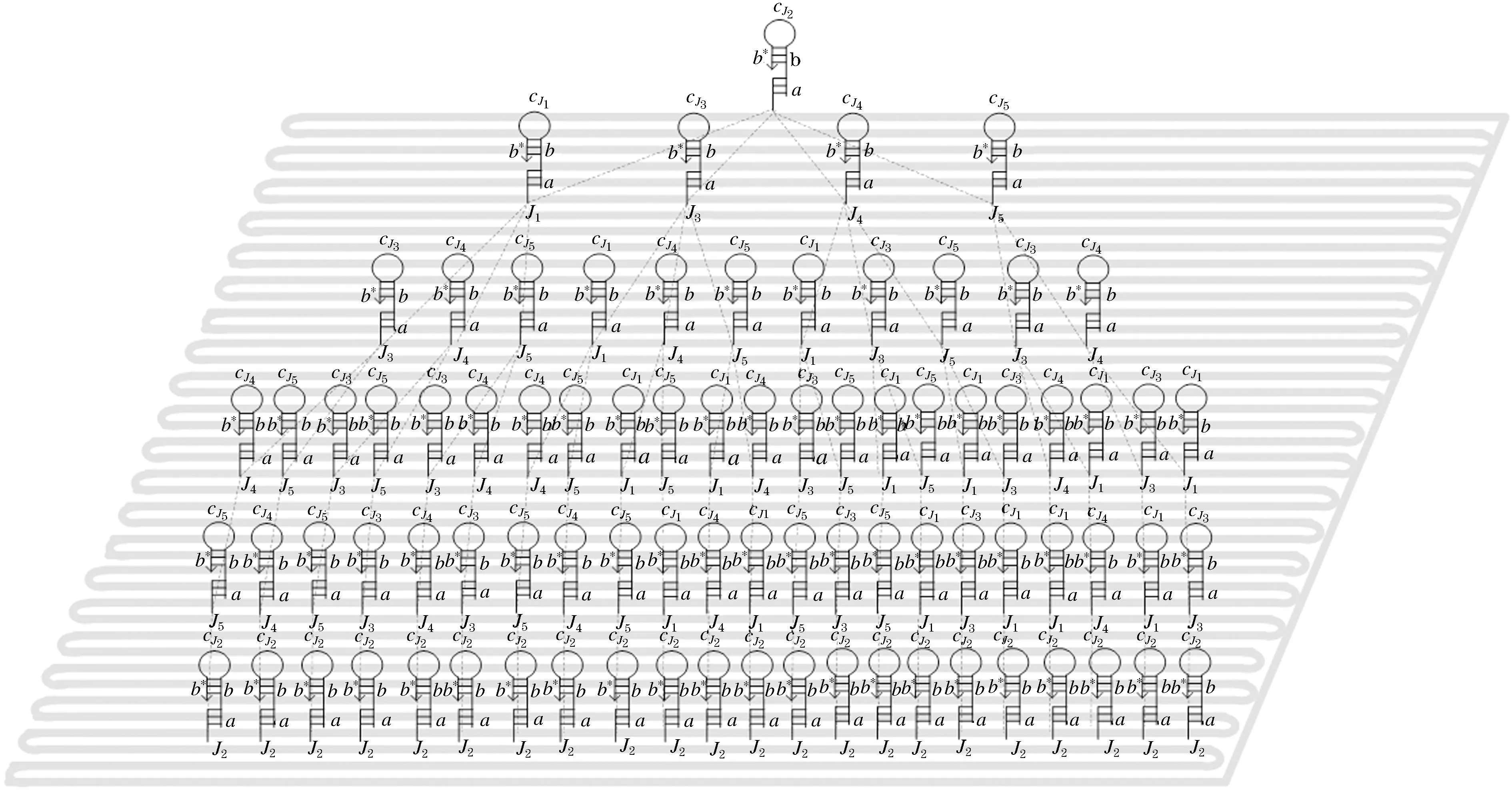
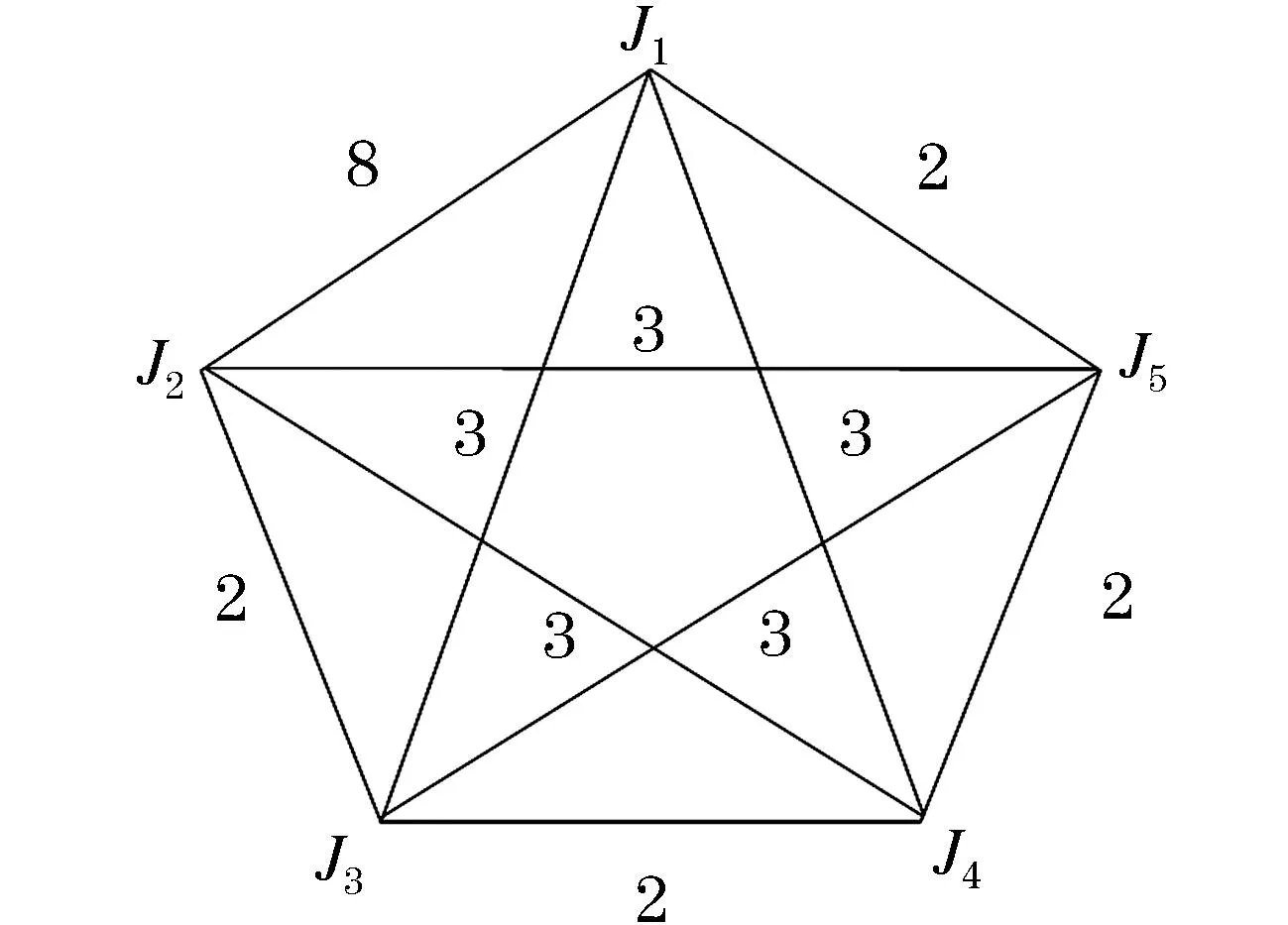
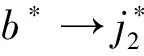
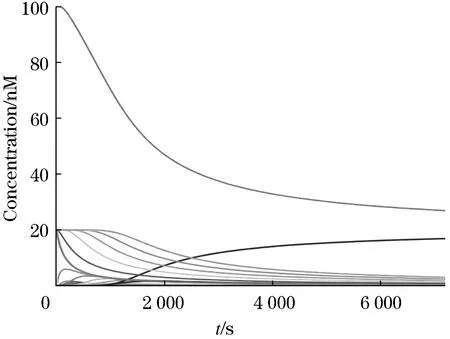
以5个城市的旅行商问题为例,每个城市分别用J1,J2,J3,J4,J5表示.每两个城市Ji和Jj间的距离用Jij表示,{Jij|i=1,2,…,5;j=1,2,…,5,i 图2 TSP问题的双向图Figure 2 Two-way diagram of the TSP problem 该模型是在矩形的二维DNA折纸基底上定义的,DNA折纸基底是通过用短链折叠环形噬菌体(M13mp18)形成(图3).在本文中,任意两个城市之间用亚稳态的发夹结构的分子信标表示,将猝灭基团和荧光基团固定在具有发夹结构DNA链的茎部的两端,并在带发夹结构的DNA链的5′端末尾设计编码,使其能够与DNA折纸基底上延伸出的订书钉链的黏性末端相互匹配(即互补配对),使得该结构能够被固定在DNA折纸基底上.在此算法中,代表任意两座城市之间距离的DNA链的权重(单位距离)可以通过分子信标来表示[18],分子信标个数即代表路径的长度. 为了达到求解旅行商问题的解的目的,第一步将问题的解空间映射成有向树T(如图4).如果此商人从J2出发,则下一个到达的城市就是J1,J3,J4,J5中的一座,依次类推进行下去.两个节点之间的长度表示了从城市Ji到城市Jj商人所需要行走的距离tij,即此树表示有向赋权树T.这样,在求解过程中,问题的解就变成了从每条根节点出发到叶片的路径中找到一条最有最小权值的路径.即为寻找权值最小的路.在此实例中,不妨假设J2作为树的根节点,则其解空间的映射如图4所示. 图4 解空间映射为树TFigure 4 The solution space is mapped to a tree T 2.2.1 DNA锚定链 研究发现,结构简单的分子信标拥有特异性强的优点,而且可荧光标记这一优势为实验提供了方便.因此在该实例中,制备DNA锚定链就可以选择具有上述描述特性的此类分子信标来进行.图5代表DNA折纸基底上对应的有向树,具体展开表示在DNA折纸基底上锚定且排列的等价形式,即为联结带有发夹结构的DNA链以及带有黏性末端的订书钉链,如图5所示.这些链囊括顶点Ji,采用分子信标代表整个顶点,能够更直观方便的观察反应.这些链包含顶点Ji(图5),从城市Ji至城市Jj距离(权值)tij用两个顶点之间的距离来代表.根据实例问题中的数值选取代表单位距离的权值,一个单位权值用对应的DNA锚定链代表.unit distance表示单位权值,它是依据4个寡聚核苷酸片段构成3′-b*-t-b-a-5′,在这里b和b*互补,在b*的末端标记上荧光基团,在b的末端标记上猝灭基团.所有这5座城市都由4个寡聚核苷酸片段组成,其中一个是根节点城市J2,J2是由4个寡聚核苷酸片段组成3′-b*-cJi-b-j2-5′,其余4座城市亦是由4个寡聚核苷酸片段构成3′-b*-cJi-b-a-5′,环部则用来代表不同的节点的区分.在图6中,延长部分表示订书钉链,a为黏性末端,可与订书钉链发生反应. 图5 5座城市对应的DNA链和表示单位权值带有荧光标记的DNA链Figure 5 The corresponding DNA strands for 5 cities and DNA strands with fluorescent markers representing unit weights 图6 折纸基底上对应的有向树Figure 6 The corresponding directed tree on the origami base 2.2.2 辅助链 参考模型求出TSP问题的答案的理论原理是:根据节点数量和权重建立求解模型,并将问题转换为有向树的形式.然后,可以利用订书钉链将锚定链按有向树的结构固定在DNA折纸基底上[19].起初,整个模型大量稳定共存于试管中,并未发生任何响应.然而当加入足量的启动链I时(如图7所示)就会发生反应,有向反应发生在哪条路径上是随机的.在这些所有可能的解中,只要找到分子信标个数最小的就是旅行商问题的最优解. 图7 启动链和辅助链Figure 7 Startup and secondary chains 假设这五座城市在DNA折纸基底上的分布呈五边形,各个边距离如图8所示. 图8 旅行商实例图Figure 8 Example diagram of traveling salesmen 商人从J2出发,到达J1,J3,J4,J5的距离分别为2、3、3、2,在DNA折纸基底上的权值表示见图9. 图9 折纸基底上J2→J1权值的表示Figure 9 Representation of J2 to J1 weights on an origami substrate 模拟DNA杂交链式反应过程的仿真软件主要为Visual DSD.主要可划分为三个模块:编码区、设置区和显示区[20].其中,设置所要进行的反应的DNA序列构成,反应的浓度和时间均在编码区实现;设置区可以选择把实验的操作模式设定为语法模式或者仿真模式; DNA序列随反应继续进行而生成的反应曲线及产物结构等方面在显示区表明.启动链记为input,DNA折纸基底记为origami,辅助链和其余辅助链的浓度各自设定为20 nM,20 nM,100 nM,20 nM,反应时间设定是7 000 s.伴随着启动链input的加入,杂交反应被诱导出现,其中辅助链率先参与启动链input反应,仔细观察图12发现,AJ2对比其他辅助链的浓度而言开始呈下降趋势.辅助链的消耗次序亦是以J2→J1→J3→J4→J5→J2此顺序逐步降低.反应进一步开展,导致中间产物的浓度先逐步上升,达到最高点后逐渐下降、最终趋于0,最终产物sp26的浓度生成速率也逐渐平稳.从根节点至子节点的有向路径是由上述产生的中间产物所对应描述的,因此在终止反应时,即从根节点到叶的有向路生成的时候,中间产物的浓度接近于0.图11表明,当启动链添加后,中间产物sp9的浓度率先抵达峰值,即6.1nM,中间产物实际为启动链I与根节点AJ2反应的生成物,在反应继续的同时,它也逐渐消失即浓度也最终接近0.最终产物sp26显示的J2→J1→J3→J4→J5→J2有向路,在反应不断进行的同时,最终产物的浓度也在相应的升高,等到反应完全结束即反应充分且终止后,生成物的浓度趋于平稳. 图12 解J2→J1→J3→J4→J5→J2的模拟结果Figure 12 Solve the simulation results of J2 to J1 to J3 to J4 to J5 to J2 本文针对J2→J1→J3→J4→J5→J2路径进行了仿真,其他路径的仿真也类似.最终,通过各路径上荧光个数就能够直观的得出旅行商问题最优解J2→J3→J4→J5→J1→J2和J2→J1→J3→J4→J5→J2. 使用此模型解决TSP问题,求解TSP问题的复杂程度极大地降低.Yuriy Brun在文献[21-22]中提出了自组装模型的复杂度计算理论,因此此模型的复杂度应该从以下两方面考虑:计算的时间复杂度和该模型所需参与计算的分子结构的种类复杂度.该模型的理论原理是利用杂交链式反应把整体的求解过程映射到DNA折纸基底上,从而直观的发生反应求解.那么通过引理可知,该模型的自组装时间和反应(树)的深度有联系,即Tim(T)=Θ(depth(T)).当前所参与杂交自组装的分子结构可大致划分为n种描述城市即顶点的分子信标,1种描述单位权值的分子信标,(n+1)种描述辅助链的分子信标以及1种启动链,综合来看利用此模型求解时所需的分子结构的种类为Num(T)=n+n+1+1=Θ(n).合理运用自组装反应的天然优势,再进一步对接该模型的实际操作过程,自然而然推出该模型的复杂度为Tim(T)+Num(T)=Θ(depth(T))+Θ(n). 本文针对旅行商问题建立了一种依据DNA折纸术和杂交链式反应的模型求解方法.将旅行商问题具体映射为有向树,将城市映射为节点,选出合适的城市即节点设为根节点.接着将有向树锚定在矩形的DNA折纸基底上,利用杂交链式反应得到所有可行解,最终求得最优解.此模型在试管中进行,加入启动链后开始反应,发夹结构打开后,反应不可逆.所以最终生成的路径均是以根节点作为首,以叶子为末的.要格外注意的是,此模型中使用分子信标的发夹结构,所以只需要在发夹结构的环部区分即可,使得设计更加便捷.最终用分子信标的个数来标定每条有向路径的权值,进一步寻找最短路径即最优解.相比较之前的求解模型而言,前者所用方法较为传统复杂,而利用生物分子计算把问题的解答步骤用生化反应的过程完全呈现,直观简单且容易操作,误差较小复杂度也能够计算,实现了该模型的可视化.在下一步的研究中,是否可以尝试运用纳米金颗粒取代分子信标更加直观的解决旅行商问题及其变体成为我们研究的重中之重.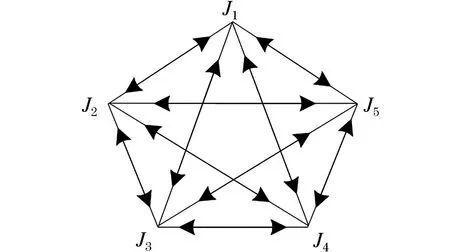


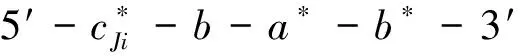
3 模型的求解


4 实例仿真
5 结 语
