路因子临界覆盖图存在的若干充分条件

袁 园

(海南大学数学与统计学院,海南 海口 570228)

在这篇文章中,我们主要考虑简单图. 本文未定义的概念和术语,读者可以参考文献[1].

设G是一个图,其中顶点集是V(G),边集是E(G).对于图G的任一点v,用符号dG(v) 表示点v的度数.给定顶点子集S⊆V(G),G[S] 表示由S诱导的图G的子图.记G-S=G[V(G)S]且κ(G) 为图G的连通度.通常,用ω(G) 和i(G) 分别表示图G的连通分支和孤立点的个数.图G的联结数定义为:

记Pn为具有n个顶点的路.图G的路因子是一个生成子图,其中每个分支是阶数至少为2的路.P≥t-因子是每个分支的阶数t≥2 的路因子.设H是一个因子临界图,如果图G=K1,或G=K2,或将图H中的每个顶点u增加一个新的顶点v作成一条新的边,那么称图G是一个太阳(sun). 具有至少6个顶点的太阳称为大太阳(big sun).用符号 sun(G) 表示图G的太阳分支的数目.如果对于图G的任意一条边e,都存在一个P≥t-因子包含边e,则称G是P≥t-因子覆盖的.文献[2]给出了 (P≥t,k)-因子临界覆盖图的概念:对于图G的任意子集S,|S|=k,如果G-S是P≥t-因子覆盖的,则称图G是 (P≥t,k)-因子临界覆盖的.

我们列出一些关于P≥t-因子的已知结果.文献[3]给出了P≥2-因子存在的充分必要条件.文献[4]刻画了具有P≥3-因子的图类.文献[5]刻画了P≥2-因子和P≥3-因子覆盖图.文献[2]给出了 (P≥2,k)-因子临界覆盖图和(P≥3,k)-因子临界覆盖图存在的充分条件.关于因子的更多结果可参考文献[6-9].

定理1[2]k≥0 是一个整数,图G满足κ(G)≥k+1.若 bind(G)>k+1,则G是 (P≥2,k)-因子临界覆盖图.

定理2[2]k≥1是一个整数,图G满足κ(G)≥k+1,|V(G)|≥k+3.若bind(G)>k+2,则G是(P≥3,k)-因子临界覆盖图.

图G称为P≥k-因子一致图,如果对任意边e1,e2∈E(G),G中存在P≥k-因子覆盖e1且避开e2.最近,文献[10]借助联结数刻画了P≥3-因子一致图.受这些结果的启发,一个自然且有趣的想法是给出(P≥2,k)-因子临界覆盖图和(P≥3,k)-因子临界覆盖图的刻画.我们的主要结果是借助连通度和联结数给出这两类图存在的充分条件,从而推广了文献[2]中的结果.

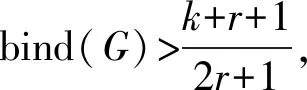
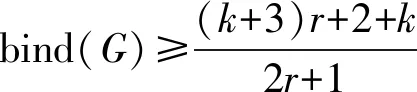
1 预备知识

在本节,为了给出主要结果的证明,需要用到下面的两个引理.第一个引理得到了P≥2-因子覆盖图存在的充分必要条件.

引理1[5]连通图G是P≥2-因子覆盖的当且仅当对于任意顶点子集X,成立

i(G-X)≤2|X|-ε1(X),

其中,ε1(X)定义为

下面的引理给出了图中存在P≥3-因子覆盖图的充分必要条件.

引理2[2]连通图G是P≥3-因子覆盖的当且仅当对于任意顶点子集X成立

sun(G-X)≤2|X|-ε2(X),

其中,ε2(X)定义为

2 定理3的证明

在本节,我们通过联结数和连通度给出了P≥2-因子覆盖图存在的条件.

如果r=0,由定理1可知定理3是成立的.接下来我们考虑r≥1.对任意子集S⊂V(G),|S|=k,令L=G-S.为了证明定理3,我们只需证明L是P≥2-因子覆盖的.用反证法,假设L不是P≥2-因子覆盖的.根据引理1,下面的式子成立

i(L-X)≥2|X|-ε1(X)+1.

(1)

接下来根据 |X| 的值进行分类讨论.

情形1|X|=0.

显然,ε1(X)=0.根据不等式(1),我们可以得到

i(H-X)=i(H)≥1.

(2)

因为κ(G)≥k+r+1,所以i(L)=0,这与不等式(2)相矛盾.

情形21≤|X|≤r.

显然地,ε1(X)≤|X|.根据不等式(1),我们可以得到

i(L-X)≥2|X|-ε1(X)+1≥|X|+1≥2.

(3)

因为κ(G)≥k+r+1,所以i(L-X)=0,这与不等式(3)相矛盾.

情形3|X|≥r+1.

注意到ε1(X)≤2,由不等式(1)可得

i(L-X)≥2|X|-1.

(4)

令E={x:dL-X(x)=0,x∈V(L)},由不等式(4)可得E≠φ且 |NG(E)|≤|S|+|X|=k+|X|.再根据不等式(4)和联结数的定义可得

(5)

这显然是一个矛盾.结论成立.

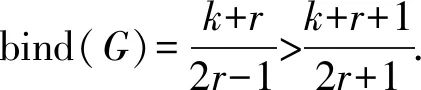
对任意S⊂V(Kk+r),|S|=k,令L=G-S.选择X=V(Kk+r)S⊂V(L),因为X不是独立集,所以ε1(X)=2.从而,i(L-X)=2r-1>2r-2.根据引理1,L不是P≥2-因子覆盖的,因此,G不是(P≥2,k)-因子临界覆盖的.

3 定理4的证明

当r=0,根据定理2,可知G是 (P≥3,k)-因子临界覆盖的.因此,我们只需要考虑r≥1 的情形.

对任意S⊂V(G),|S|=k,令L=G-S.为了证明定理4,接下来证明L是P≥3-因子覆盖的.用反证法.假设L不是P≥3-因子覆盖的.根据引理2,可以得到

sun(H-X)≥2|X|-ε2(X)+1

(6)

对某个子集X⊆V(G) 成立.现在我们考虑下面的4种情形.

情形1|X|=0.

在这种情形下,ε2(X)=0.借助不等式(6),下面的式子成立

1≤sun(L-X)=sun(L)≤ω(L)=1,

这意味着 sun(L)=ω(L)=1.

论断L是一个大太阳.

否则,L=K1或L=K2.从而|V(G)|=|S|+|V(L)|≤2+k,这与 |V(G)|≥k+3 相矛盾.

根据上面的论断,记F是L的因子临界图,则有 |V(L)V(F)|=|V(F)|≥3,从而可以得到

情形21≤|X|≤r.

显然,ε2(X)≤|X|.根据不等式(6),我们可以得到

1=ω(L-X)≥sun(L-X)≥2|X|-ε2(X)+1≥2,

产生矛盾.

情形3|X|=r+1.

在这种情形下,ε2(X)≤2.根据不等式(6),可以得到

sun(L-X)≥2|X|-ε2(X)+1≥2r+1.

(7)

子情形3.1L-X有一个非太阳的分支Y.

子情形3.1.1a≥1.

令W=V(Y)∪V(aK1)∪V(bK2)∪V(T1)∪…∪V(Tc),其中a,b,c分别表示孤立点、K2和大太阳分支的个数,从而

且

根据联结数的定义,我们可以得到

子情形3.1.2a=0.

令M=V(Y)∪V(bK2)∪V(T1)∪…∪V(Tc),其中a,b,c分别表示孤立点、K2和大太阳分支的个数,则存在点x,y∈V(M) 满足dM(x)=1,xy∈E(M).

因为

和

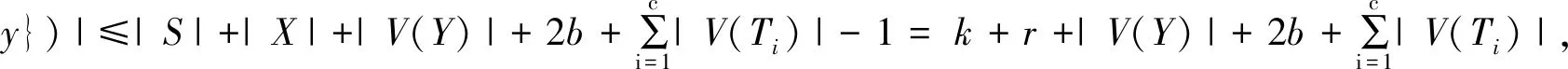
所以

子情形3.2L-X没有非太阳分支.

在这种情形下,我们可以得到

sun(L-X)=a+b+c≥2|X|-ε2(X)+1≥2r+1.

子情形3.2.1a≥1.

令P=ak1∪bK2∪T1∪T2∪…∪Tc,其中a,b,c分别表示孤立点、K2以及大太阳分支的数目.结合联结数的定义,可以得到

子情形3.2.2a=0.

从而得到

这与条件

(kr+r+k+1)(4r+1)-(2r+1)(k+r+1)=2r2+2kr+4kr2+2r>0相矛盾.

情形4|X|≥r+2.

显然地,ε2(X)≤2.借助不等式(6),我们可以得到

sun(L-X)=a+b+c≥2|X|-ε2(X)+1≥2|X|-1.

(8)

令a,b,c分别表示孤立点、K2以及大太阳分支的数目.

子情形4.1b+c=0.

在这种情形下,容易得到a≥2|X|-1.根据联结数的定义,可以得到

子情形4.2b+c≥1.

令P=(bK2)∪V(T1)∪…∪V(Tc).则存在两个顶点x,y∈V(P) 满足dP(x)=1,xy∈E(P).

根据联结数的定义,下面的式子成立

注3条件κ(G)≥k+r+1 不能用κ(G)≥k+r替换.

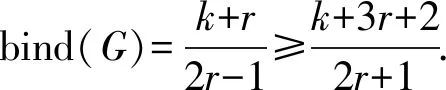
sun(L-X)=2r-1>2|X|-ε2(X)=2r-2.

通过引理2,L不是P≥3-因子覆盖的.因此G不是 (P≥3,k)-因子临界覆盖的.