基于特征选择和组合预测模型的负荷短期预测方法
2023-12-19陆嘉华华昊辰
陆嘉华,梅 飞,杨 赛,唐 瑜,华昊辰
(河海大学能源与电气学院,江苏 南京 211100)
构建新型的电力系统是实现“双碳”目标的重要途径,进行准确高效的短期负荷预测是实现电力系统安全稳定经济运行的重要条件[1]. 由于大量分布式电源在负荷侧并网数目增加,气象、日期等外部因素的影响进一步增加了负荷不确定性[2]. 为了提高配电网运行的稳定性和运行效率,对负荷影响因素进行特征优选,进而构建合理的负荷预测模型是实现这一目标的重要措施.
短期负荷预测是指预测未来数小时至数天的负荷大小,对电力系统运行、控制、调节等具有重要意义[3]. 目前针对负荷短期预测问题已有许多研究. 短期负荷预测方法可分为数学统计方法、机器学习方法和深度学习方法[4],预测形式可分为确定性预测[5]和不确定性预测[6].
在构建负荷预测模型时,选择适当的气象特征对模型性能的研究至关重要[7]. 通常采用经验法[8]和相关性分析[9]来选择这些特征,这些方法具有高效性且应用广泛. 此外,过滤法使用互信息(mutual information,MI)或皮尔逊相关系数来构建特征子集,以修正特征输入[10-11]. 然而,这可能导致特征之间的冗余性. 部分研究结合过滤法和包装法以提高准确性,同时也增加了模型训练时间[12]. 为了解决特征选择和冗余性问题,一些研究使用正则化方法,通过模型权重来约束不重要的特征,使它们的权重趋近于零[13],从而提高了模型的泛化性能.
在时间序列预测中,深度学习方法相对于传统方法更能挖掘负荷的非线性特征. 循环神经网络及其改进算法被广泛用于提取时序特征. 时域卷积神经网络(temporal convolution network,TCN)[14]能够提取短时特征,而WaveNet模型则处理长负荷时间序列[15]. 有些研究将卷积神经网络(convolutional neural networks,CNN)与长短期记忆(long short-term memory,LSTM)神经网络相结合以提取不同时间尺度的特征[16],或将CNN与门控循环单元(gated recurrent unit,GRU)结合,以提高运算效率[17]. 组合预测模型是提高模型泛化性能的一种方法. 分解算法和优化算法分别用于构建时序特征和调整超参数,显著提高了模型性能[18],或采用分层预测模型或通过分解算法构建不同分量的预测模型,最后将它们的预测结果相加以获得最终结果[19-21].
本文针对配电网负荷短期预测问题构建了BP回归模型与CNN结合双向门控循环单元(Bi-directional gated recurrent unit,BiGRU)时间序列模型的组合预测模型. 首先针对多维气象特征的选择问题提出了一种特征选择流程,基于特征选择结果分别构建回归和时序预测模型的气象特征输入. 该组合预测模型第一部分通过BP回归模型学习日期特征和实时气象特征来拟合实际负荷值;第二部分构建时间序列模型,将历史气象和历史负荷时序特征作为时序模型输入特征,输出负荷预测值;第三部分构建负荷短期预测模型,以前两部分模型负荷预测结果作为模型输入,同时考虑日类型特征,基于BP神经网络输出最终负荷预测值. 通过对某地配电网10 kV母线预测算例分析,本文特征选择方法提高了预测的准确性,组合预测模型相较于单一回归或时间序列模型具有更低的预测误差,对负荷变化趋势较大的非工作日预测效果有明显改善.
1 气象特征选择
作为模型的特征输入集合需要考虑特征与负荷之间的相关性、特征之间的相关性大小即冗余性和多个特征的协同作用[22],通过综合考虑特征三部分作用计算特征增益大小来选择特征加入最优特征子集中,使用最优特征子集构建模型可以提高模型预测准确性.
1.1 最优特征集增益
考虑单个特征与负荷相关性,使用MI计算单个特征与负荷相关性以及特征之间的冗余性大小. 针对连续特征变量,互信息基于信息理论计算相关性,能够很好的描述变量之间线性及非线性关系大小. 互信息的值越大变量之间的相关性越高,互信息为0时说明变量之间相互独立. 两个连续随机变量之间互信息计算公式如式(1):
(1)
式中,X1、X2为两个连续随机变量,p(x1)为变量X1的概率密度函数,p(x2)为变量X2的概率密度函数,p(x1,x2)为两个随机变量联合概率密度函数.
(1)相关性计算.单个气象特征与负荷互信息大小计算公式为:
Ci=MI(Xi,Y),Xi∈RF,
(2)
式中,Xi为原始特征集RF中第i个特征,Ci记作第i个气象特征与负荷的互信息大小.Ci越大说明该气象特征与负荷相关性越强.
(2)冗余性计算.最优特征集记作OF.使用Ri评价原始特征集中的单个特征Xi加入最优特征集后的特征冗余性,计算公式为:
OF={X1,X2,…,Xm},
(3)
(4)
式中,Xj为最优特征集中第j个特征,原始特征集合选择的单个特征Xi与最优特征子集的冗余性,选择具有较小的冗余性特征,避免了最优特征集中同时选择多个相似特征.
(3)协同作用计算.协同作用指多个气象特征变量同时对负荷变量的作用,用复相关系数度量,复相关系数越大,相关性越强.复相关系数用于描述最优特征集对标签的作用大小,基于多元线性回归模型求得,计算公式为:
(5)
式中,yt为真实标签值,对应实际负荷值;ya为真实标签值的平均值,yr为多元线性回归的回归值.考虑原始特征集的单个特征Xi加入最优特征集,多元线性回归值的计算参考式(6),进一步计算协同作用大小Si,如式(7)所示:
yi=mlr({Xi}∪OF,y),
(6)
Si=r(yi,y),
(7)
式中,mlr表示多元线性回归模型,自变量为最优特征集和原始特征集中第i个特征的并集,y为回归方程因变量即负荷真实值,yi对应回归方程回归值.
(4)特征集增益计算.若考虑将原始特征集中单个特征Xi加入最优特征集中,此时的最优特征集增益可写作Gi,计算公式如下:
Gi(α,β,Xi)=Ci-αRi+βSi,
(8)
式中,Ci为原始特征集中气象特征Xi与负荷相关性大小,Ri为气象特征Xi加入最优特征集中的冗余性大小,Si为气象特征加入最优特征集后的协同作用大小,α和β分别为控制冗余性和协同作用的权重系数.通过权重系数来控制单个气象特征Xi加入最优特征集时的增益正负.当Ci大于0时特征集增益为正,反之为负.
1.2 特征选择流程
原始气象特征集由两部分构成,一部分是气象站采集的气象数据中包含的各个气象特征,另一部分包括考虑气象耦合作用的综合气象因素影响,耦合气象因素包括热指数、温湿指数、风寒指数和人体舒适度指数[23],特征集中各气象特征符号及其含义如表1所示.

表1 气象特征符号及含义
将原始特征集合记为RF,写作:
RF={GHI,UVI,T2M,T2MD,T2MW,QV2M,RH2M,PP,PS,WS10M,WD10M,HI,THI,WCI,CIHB}
(9)
基于原始特征集中单个特征加入最优特征集中的特征集增益正负,为正时将该特征加入最优特征集,同时从原始特征集中去除;增益为负时则将该特征直接从原始特征集中去除;再进行下一步迭代,直到原始特征集合为空集结束,输出的结果为最优特征集,记作OF.特征选择流程如图1所示,特征选择流程如下所述.

图1 特征选择流程图
第一步:输入初始数据原始特征集RF、最优特征集OF、权重系数α和β;
第二步:从原始特征集中选择具有最大相关性的特征作为最优特征集的初始特征;
第三步:从原始特征集中选择具有最大相关性的特征,计算最优特征集增益,若增益大于0,则将该特征加入最优特征集,同时从原始特征剔除该特征,反之则直接从原始特征剔除该特征;
第四步:判断原始特征集是否为空,满足条件时结束程序,输出最优特征集,反之则跳转至第三步.
将选择流程中冗余性和协同作用权重系数α和β视为预测模型超参数,通过粒子群优化方法(particle swarm optimization,PSO)确定权重系数α和β,分别为0.212和0.017,得到最优特征集OF为紫外线指数、地表2 m处干球温度和相对湿度,写作:

表2 时间日期特征符号及含义
OF={UVI,T2M,RH2M},
(10)
2 负荷组合预测模型
2.1 组合预测模型
组合预测模型包含三个部分,其结构如图2所示:第一部分为BP回归预测模型,第二部分为CNN-BiGRU时间序列预测模型,第三部分为组合预测模型. BP回归预测模型对影响负荷的日期时间特征和未来气象特征进行解释,而CNN-BiGRU学习历史负荷和累积气象因素时间序列中的时序信息.

图2 负荷组合预测模型
BP回归模型能够较好的拟合非线性特征,但对于历史负荷中时序特征提取不足,也没能考虑气象因素累积效应,因此本文负荷预测模型采用时间序列预测模型与BP回归预测模型结合构建的组合预测模型,以增强预测模型对不同时序特征学习能力.
2.2 回归预测模型
针对负荷预测的实时特征量,如已知天气预报值和预测点的日期、时间、特殊日特征,可以利用BP神经网络较强的非线性拟合能力,建立多元回归模型,学习不同特征波动在某个时刻值对负荷大小的影响. 回归模型的气象特征输入为特征选择后的最优特征集OF,考虑负荷具有非常强的时间周期性特点,据此建立回归模型的时间输入特征如表2所示.
动态气象特征赋权结构将日期时间变量通过编码层输出气象特征权重矩阵,用模型气象特征输入乘该权重矩阵,用于控制气象特征在不同日期时间下输入大小[10]. 如图2第一部分所示,将加权后的气象特征向量与时间日期特征融合作为回归预测模型的特征输入,最后输出预测结果.
加权结构编码层由多层神经网络全连接层组成,如图3所示. 输出时变特征权重矩阵[ω1,ω2,…,ωm],将气象特征矩阵[X1,X2,…,Xm]加权.
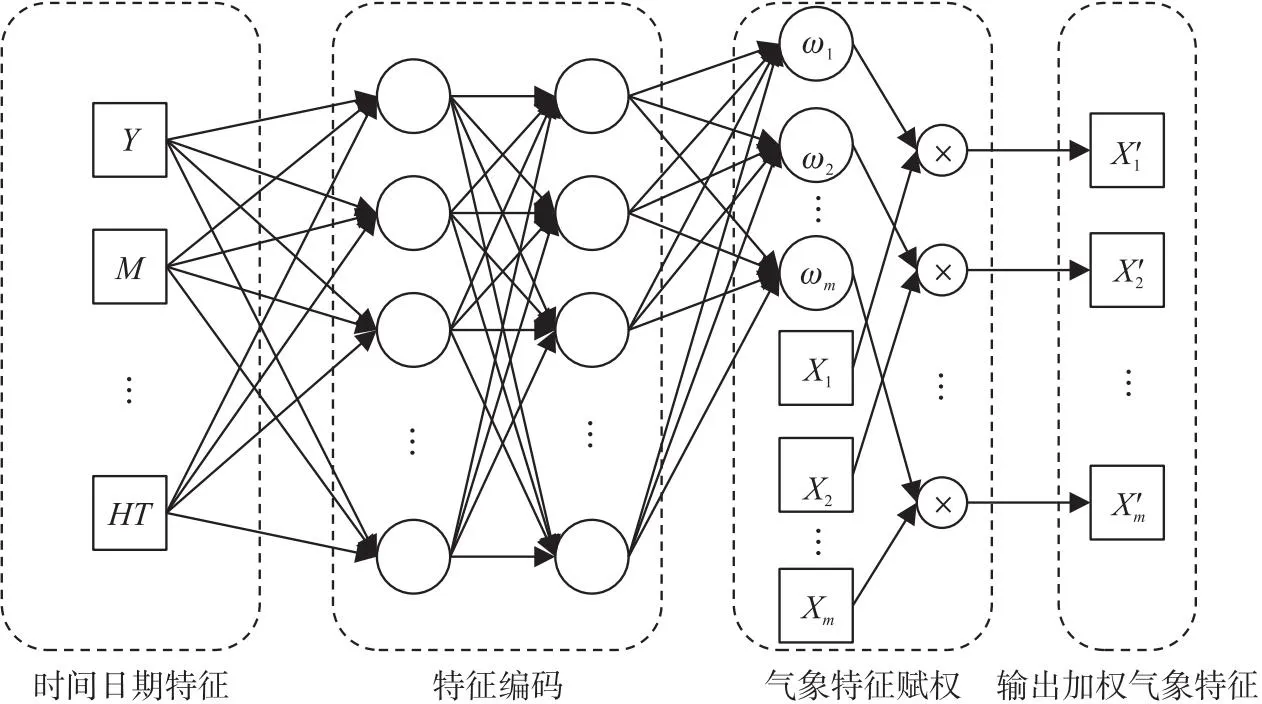
图3 气象特征动态加权结构
记日期时间特征集为DF,将特征输入记为XDF,考虑仅一层隐含层编码结构,动态气象特征赋权过程可写作:
[ω1,ω2,…,ωm]=φ(XDFW+b),
(11)
[X′1,X′2,…,X′m]=[ω1,ω2,…,ωm]⊙XOF,
(12)
式(11)中,XDF为日期时间输入向量,W为编码层权重系数矩阵,b为编码层的偏置项向量,φ为激活函数,ω为动态特征权重.式(12)为特征赋权过程,m为OF中元素个数,对两向量进行哈达玛积运算,结果即为加权气象特征向量.
将加权后的气象特征与时间日期特征分别由各自的编码层进行编码,得到两个相同维度的编码特征向量,通过向量拼接来实现两部分特征融合,其计算过程如式(13):
X=[X′OFW′OF+b′OF,XDFWDF+bDF],
(13)
式中,X为两部分特征融合后的特征向量,即BP神经网络的输入;X′OF为加权气象特征,W′OF与b′OF分别对应其编码层的权重系数矩阵与偏置项向量;相应的,WDF与bDF分别对应时间日期特征输入编码层的权重系数矩阵与偏置项向量.
2.3 时间序列预测模型
GRU简化了LSTM模型的输入结构,降低了模型复杂度,同时采用双向结构来增强时序特征前后时序信息联系. 一维CNN与循环神经网络结合模型用于学习长时间序列信息,且在负荷预测中取得了较好的效果[24],一维CNN计算定义如式(14):
(14)
式中,Ti为输入时序特征,⊗为卷积运算,Ki为第i个滤波器的卷积核函数,b为偏置项,φ为激活函数.
时序预测模型中GRU结构的每个时间步长状态参数计算如公式(15)-(18):
(15)
(16)
(17)
h=z*h′+(1-z)*g,
(18)
式中,z为更新门,r为重置门;g为先前状态门控制器,h为当前时间步的激活状态,h′为上一时间步激活状态,x为当前时间步输入特征向量;Wz、Wr、Wg分别为对应门控制器权重矩阵,bz、br、bg分别为对应门控制器的偏置项.
BiGRU以GRU为基础加入双向循环神经网络结构,学习时序特征时包含前向和反向两个传播方向,加强了GRU模型对时序特征的提取能力. 参考图4中BiGRU结构,计算公式如式(19)-(21)所示:
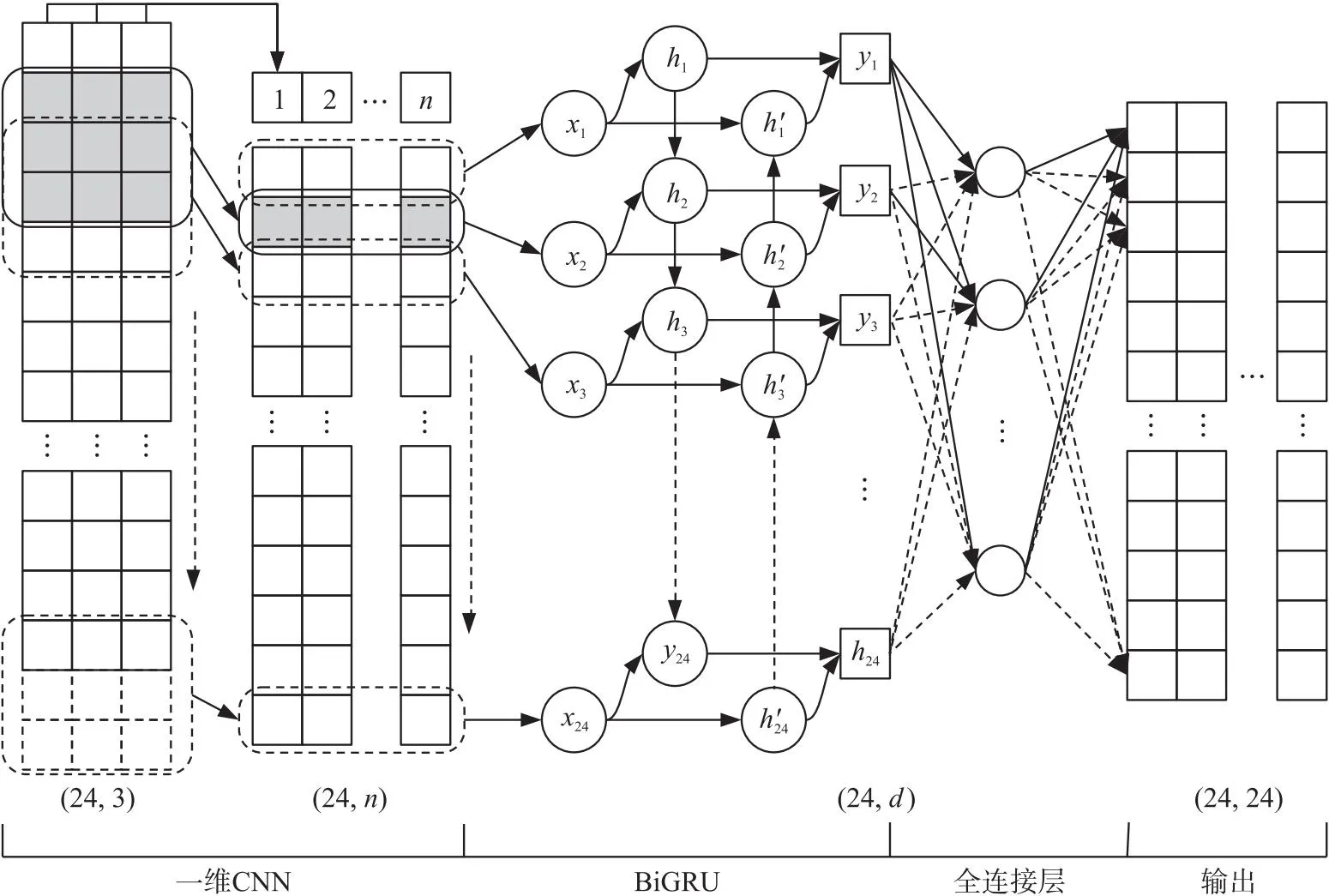
图4 CNN-BiGRU模型结构
yt=φ1(W1ht+W′1h′t),
(19)
ht=φ2(W2xt+W3ht-1),
(20)
h′t=φ2(W′2xt+W′3h′t-1),
(21)
式中,xt和yt分别为第t时间步输入和输出,ht、ht′分别为第t时间步的前向层和反向层的输出状态量;W1和W1′分别为前向和反向状态量映射至输出层权重矩阵;W2和W2′分别为输入量映射至前向和反向状态量的权重矩阵;W3和W3′分别为第t-1时间步前向和反向状态量映射至第t时间步状态量的权重矩阵;φ1和φ2分别为前向和反向两个方向的激活函数.
3 算例分析
3.1 预测评价指标
本文使用的误差评价指标采用平均绝对百分比误差(mean absolute percentage error,MAPE)、平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE),用于评价不同预测模型的预测准确性,同时采用确定性系数(coefficient of determination,R2)评价模型回归预测能力,即预测变化趋势.
3.2 实验数据集
本文实验数据集采用江苏省宿迁市某配电网10 kV母线负荷数据,数据包含工业负荷、部分商业负荷和居民负荷;负荷数据采集时间为2019年1月1日至2021年12月31日,分辨率为15 min. 负荷所在地的气象数据来源于NASA公开气象数据网站,数据时间跨度与负荷数据保持一致,分辨率为1 h,各个特征类型及含义见表1. 对负荷数据进行降采样,使负荷采集间隔与气象数据保持一致.
数据中连续缺失值采用相邻两日同一时刻的数值的平均值进行填充,对不同量纲数据进行最小最大归一化处理.
3.3 模型参数设置
本文实验特征选择方法基于Skit-learn框架构建,负荷回归预测模型和时间序列模型均基于Keras和Tensorflow平台搭建. 实验提取数据集最后31天用于测试集,剩余数据按7∶3划分为训练集和验证集. 预测方式为短期预测中的日前预测,其预测间隔为1 h,共有24个时间点负荷值. 实验通过实际日负荷数据更新预测,对最后一个月31天的负荷值进行预测. 各模型参数设置如表3所示.

表3 模型主要参数
模型中间层由多层神经网络叠加,回归模型和组合模型的实际堆叠层数为3层,每层单元个数分别为200、100和50,激活函数采用LeakyReLU,其计算公式如式(22)所示:
(22)
式中,x为激活函数输入变量,λ为斜率系数,λ>0,本文模型中λ取0.01.
模型训练学习率均采用指数调度形式,优化方式采用Adam算法. 对比模型的参数设置与本文模型参数设置基本一致. 时间序列模型中间层堆叠层数为4层,激活函数采用tanh,模型数据结构变化如图5所示,Bs为Batch size大小.

图5 模型各层数据结构变化图
为验证本文方法的有效性,首先针对不同特征选择方法对模型性能的影响进行分析,分别采用Pearson、MIC、随机森林回归(random forest regressor,RFR)特征排序方法和本文特征选择方法结合回归预测模型进行预测性能对比,再将本文组合预测模型分别与文献中常用时序模型进行对比,包括LSTM、GRU以及CNN-GRU、CNN-BiLSTM、CNN-BiGRU,分别简化为CGRU、CBiLSTM、CBiGRU.
3.4 特征选择
通过本文特征选择方法对原始特征集中特征进行选择得到最优特征子集,特征选择方法中超参数α和β由PSO参数优化方法基于训练集和验证集确定,种群大小为20,迭代次数为150,随机化粒子初始位置,最大速度为0.01,目标函数为模型预测误差.
为对本文特征选择方法的有效性进行检验,对比特征选择方法采用Pearson相关系数、MIC相关性和RFR对特征重要程度进行排序,用相关性大小阈值或特征重要程度阈值得到特征选择结果,结合BP回归预测模型进行负荷预测,计算误差进行对比分析.
Pearson相关系数和MIC特征选择的结果相同. 从表4中不同特征选择方法的预测结果可以看出,本文提出的特征选择方法具有最小的预测误差,同时对负荷的变化趋势拟合效果也具有一定的提升效果.

表4 各特征选择方法预测性能
从表4的结果可以看出,基于相关性大小的Pearson和MIC特征选择方法和RFR方法无法对特征的冗余性进行限制,故同时选择了辐照度和紫外线指数两个特征. 本文的特征选择方法同时考虑了特征多个因素,本文特征选择流程提高了模型的预测准确度.
由图6中整体预测效果可以知道回归模型相较于时序预测模型效果较差,在12月1日至4日输入特征变化仅在日特征、时特征和气象特征,故预测结果也较为平稳,5日回归模型输入中含有节假日和日类型信息,在负荷水平显著降低时实现了较好的拟合效果.
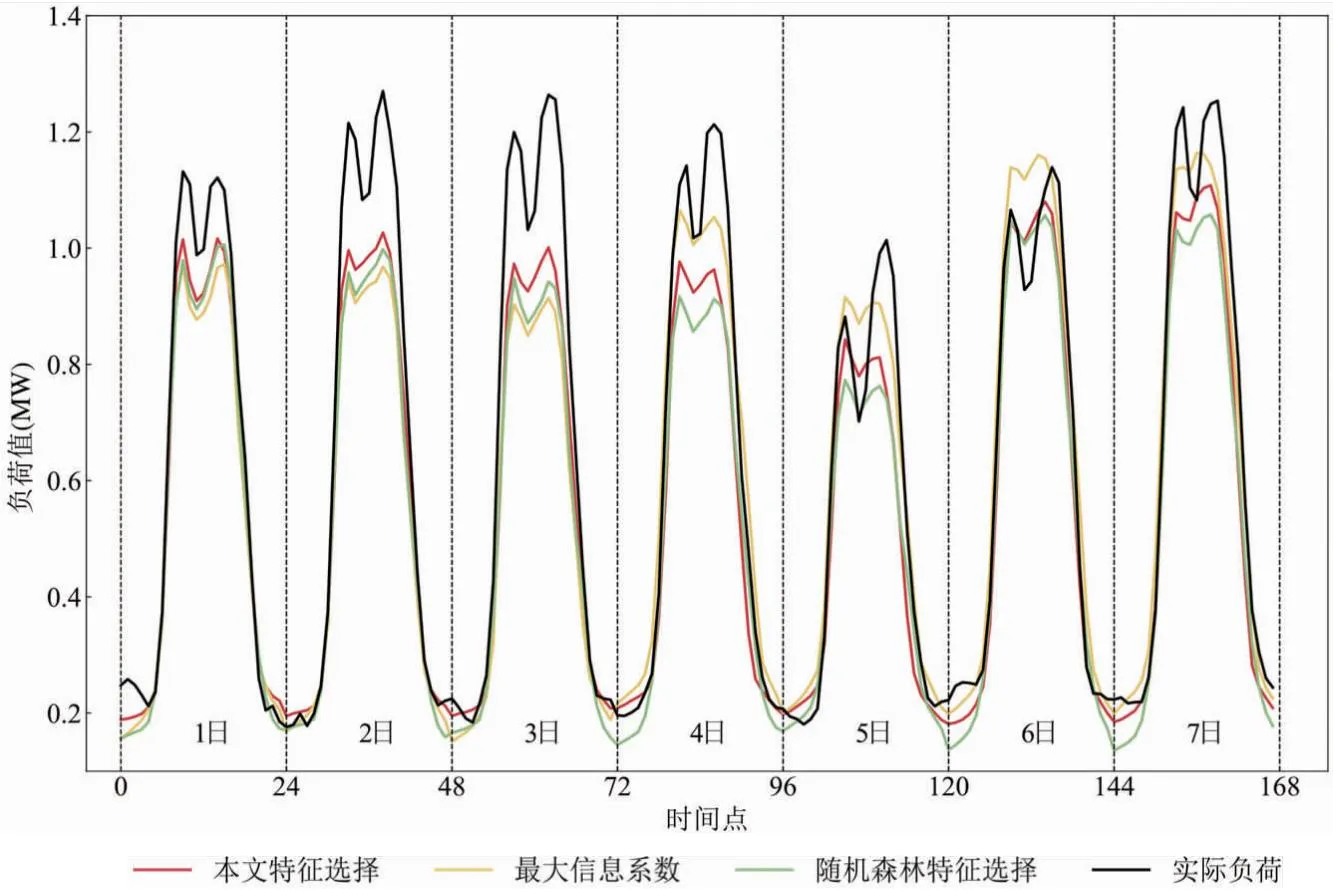
图6 各特征选择方法1至7日回归预测曲线
3.5 组合预测模型
对于本文所提出的组合预测方法,对比模型选择负荷预测中应用广泛的时间序列模型,预测结果统计如表5所示.
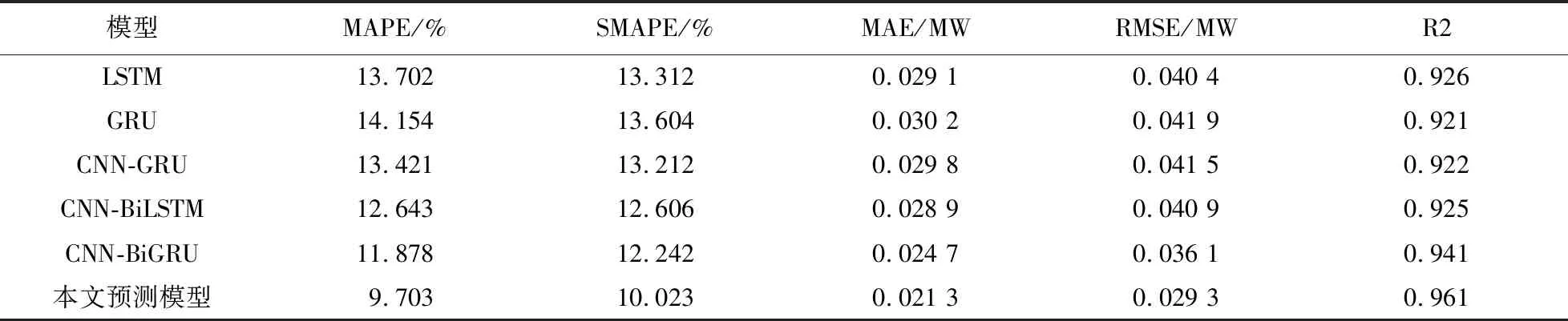
表5 各模型负荷预测性能
根据各个模型总体预测性能结果,本文预测模型在各性能评价指标上都好于其它传统预测模型及其改进模型,验证了本文方法对准确性的提升作用. 传统时序预测模型中加入卷积层对模型的预测准确度具有一定的提升作用,且具有双向结构的模型相较于没有双向结构的模型的预测准确性提升较为显著. 相同模型结构和参数下,使用BiGRU算法改善了传统双向循环神经网络的预测效果.
通过分析预测结果中12月1日至7日,这段时间包括4个工作日和2个周末日,如图7所示. 对比图6 所示回归模型预测结果,时序预测模型在负荷日内的预测趋势表现良好,表明时序模型具有出色的预测性能.
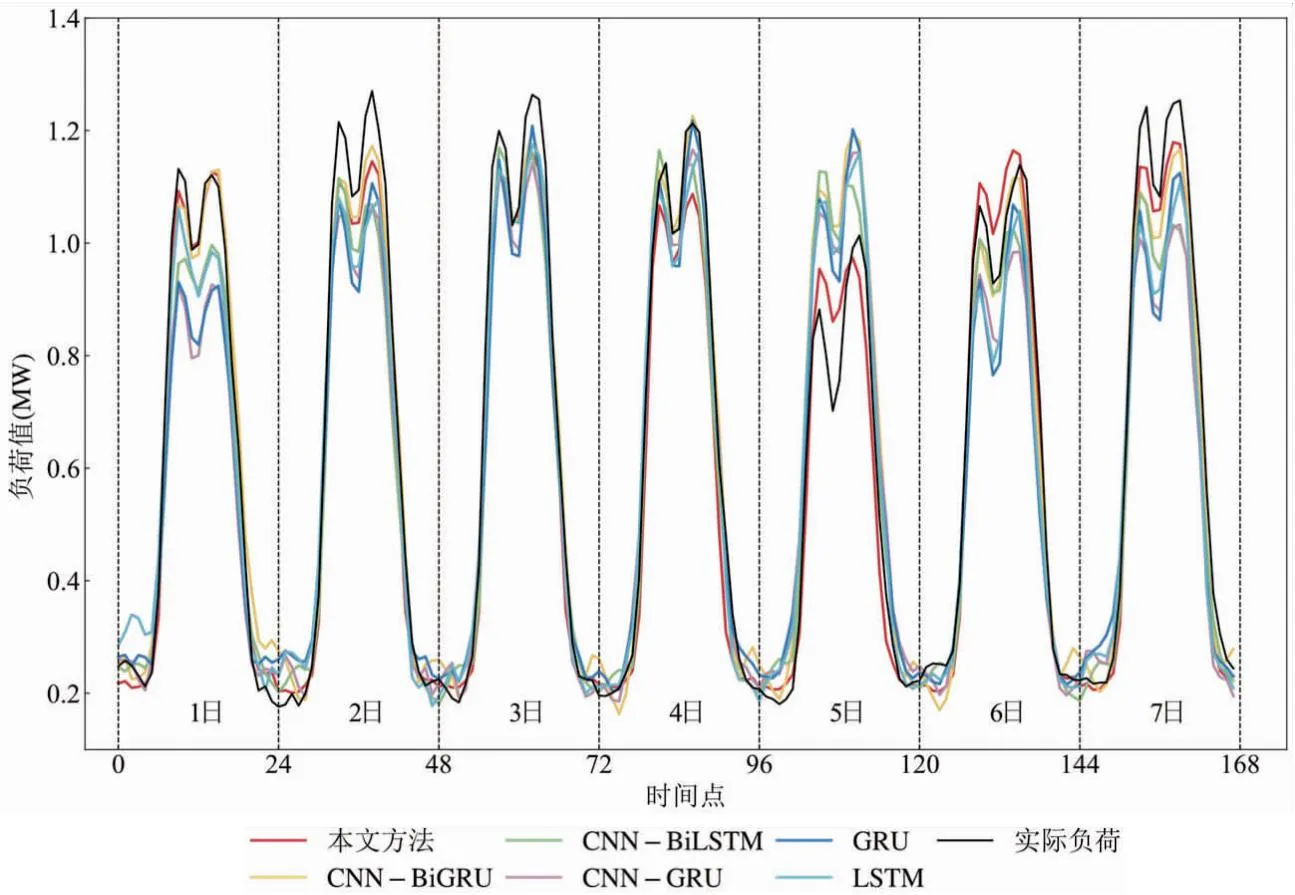
图7 各模型1日至7日预测曲线
从图8中可以观察到,不同模型在12月1日、2日和5日的预测误差存在明显差异. 特别是加入卷积层的CGRU模型在负荷谷值处的预测效果优于GRU模型,而加入双向结构的CBiGRU模型在峰值处的拟合效果明显提高. 根据实际负荷曲线可以看出12月4日的负荷相对于前一天的变化较小,而从4日到5日的实际负荷有明显下降趋势. 时序模型的预测受到前一天负荷大小的影响,导致5日负荷峰值处的预测结果偏高.

图8 各模型1至7日每日预测MAPE
回归预测结果和表6中的性能对比表明,本文方法利用组合模型中的回归模型学习时间日期和节假日的特征,较好地捕捉了周末负荷变化趋势,从而提高了对周末负荷的预测性能.
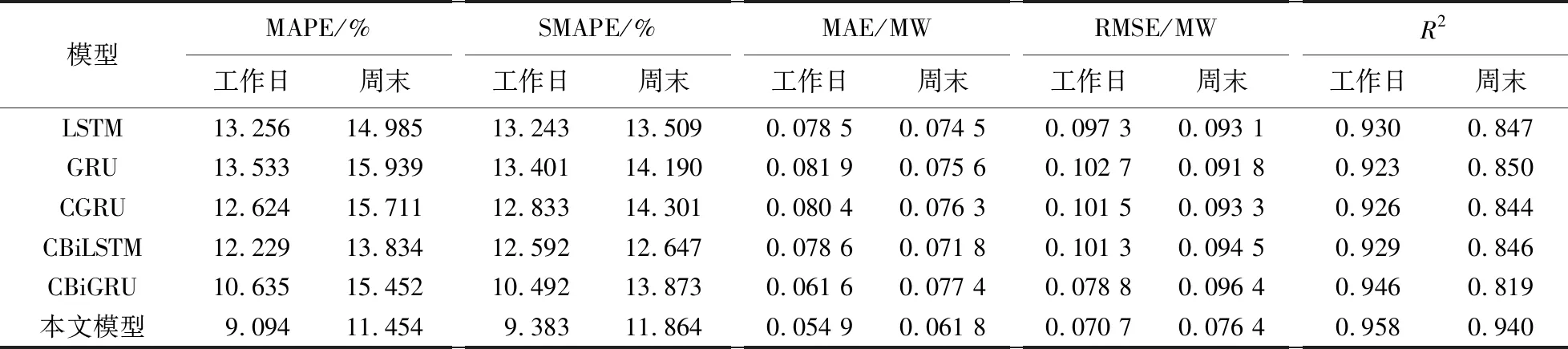
表6 各模型不同日类型平均预测性能
4 结论
本文提出了基于组合预测模型解决配电网母线短期预测问题,构建特征选择方法对影响负荷的多个气象特征进行优选,通过在配电网10 kV母线负荷进行预测分析得到以下结论:
(1)本特征选择方法能够从多个气象特征中选出与负荷相关性最大、特征之间冗余性最小和具有最大协同作用的最优特征集,相较于传统相关性特征选择方法降低了模型预测误差;
(2)加入卷积神经网络和双向循环神经结构的时序模型能提升模型时序预测能力;
(3)本文方法利用回归与时序模型结合的组合预测模型对影响负荷特征进行不同时间维度的学习,总体预测结果相比于最优卷积时序模型的MAPE降低了18.31%,且对于变化趋势较大的周末负荷预测MAPE的误差降低了17.20%.
