带非线性扩散的趋化-趋触模型解的大时间行为
2023-12-19刘锦涛
刘锦涛,贾 哲
(临沂大学数学与统计学院,山东 临沂 276005)
本文研究如下带非线性扩散的趋化-趋触模型
(1)
解的大时间行为.其中Ω⊂R3是带光滑边界的有界域,u,v,w分别代表癌细胞密度、基质降解酶浓度和细胞外基质浓度.H(u),S(u)分别代表趋化敏感项和趋触敏感项.在本文中假设H,S满足如下条件:
H(s)≤χs(s+1)-α,其中s≥0且H(0)=0,
(2)
S(s)≤ξs(s+1)-β,其中s≥0且S(0)=0,
(3)
式中,χ,ξ,α,β>0.另外,假设初值满足

(4)
2016年,Chaplain等[1]提出肿瘤细胞的运动依赖于随机扩散、趋触运动和基质降解酶的扩散梯度,并引入了趋化-趋触模型.之后该方程被广泛关注(参见文献[2-10]).当m=1,H(u)=S(u)=u时,Zheng等[2]研究了解的整体存在性和大时间行为.另外,当0 本文主要研究模型(1)弱解的大时间行为,主要结果如下: 首先回顾模型(1)弱解的整体存在性和有界性结果: 式中,C是与μ无关的常数. 下面介绍在定理1的证明中起到重要作用的两个引理: 引理2[2-3]假设0 引理3[6]假设h(t)∈L1(T,∞),其中T>0,h≥0.如果存在常数C>0使得 h(t)-h(s)≤C(t-s),其中t>s>T或h(t)-h(s)≥-C(t-s),其中t>s>T, 受文献[2-3,7]启发,定义下面的能量泛函: 则F(t)满足下面的引理: 证明经计算得 这意味着 再通过模型(1)的第三个式子,然后结合引理1和引理2我们得到 以及 因此,我们得到 (5) 对该式关于时间t在(1,+∞)上积分,得到 上式用到结论-Δw(x,t)≤‖w0‖L∞(Ω)v(x,t)+D,(x,t)∈Ω×(0,Tmax),其中D是正常数(见文献[8]).结合引理1得 进而由引理3和4得当t→∞时, 再利用Hölder不等式得对任意的p≥2,有 另外,结合模型(1)的第二个式子和引理 1得 利用引理3和4,同样得到当t→∞时, 再通过Gagliardo-Nirenberg不等式得当t→∞时, 证毕.
1 预备知识

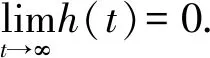
2 定理1的证明



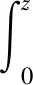

3 结论

