基于复数FastICA的双极化干扰对消算法研究
2023-12-18潘帅帅孙中传
潘帅帅,武 铮,王 烁,孙中传
(1.中国电子科技集团公司第三十八研究所,安徽合肥 230088;2.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001)
0 引 言
现如今卫星通信技术愈加成熟,卫星通信相关业务已经广泛地渗入到人们的日常生活中,如卫星电视、卫星导航、卫星遥感数据监测等。在技术层面上,为了更好满足人们对网络数据的需求量,同时在不增加频谱等相关资源的利用率且提高数据传输速率的情形下,相关技术人员在卫星通信信号收发的过程中利用电磁波的极化这一特性,采用极化复用技术来传输信号[1-3]。但在实际工程实践中,由于雨衰、极端天气、天线隔离度设计等因素使得传输信道变得非理想,不论是线极化还是圆极化,都会使得接收端在接收信号时,发生“交叉极化干扰”情况,即接收到的一个极化信号中混杂其他极化信号,这使得原先的一个极化信号所携带的信息可能会出错,进而影响传输性能。
为解决交叉极化干扰问题,目前已有研究人员提出了相应的解决办法。文献[4]提出了跟踪信道性能变化的NIRLS-XPIC 算法,在基带实现交叉极化干扰对消,采用均衡和抵消并行的结构,收敛速度快但需要增加一定的计算复杂度。文献[5-6]从双极化MIMO 角度来研究交叉极化并做出了分析和仿真,验证了单星系统通过双极化MIMO传输可改善交叉极化的影响并提升系统传输性能。文献[7]提出了一种从多个维度进行搜索的极化对消算法并进行了仿真,该方法在实际应用时能提高极化对消处理过程中对路径延迟和频差等因素的适应性,但搜索维度大使得硬件实现困难。文献[8]提出了采用基于LMS 的检后盲自适应的XPIC 算法并进行理论分析和仿真,对工程实践具有指导意义。文献[9]提出一种高速数传解调器中的基于自适应滤波器交叉极化干扰对消方案,仿真验证了该对消方法适用于多载波多调制信号间的交叉极化干扰,但在硬件资源上需要额外开支。文献[10]提出了基于相关函数的极化对消算法,并在中频和基带上进行了性能的比较,得出在基带实施算法具有优势的结论,但基带的相位偏差会导致相关函数估计不准确而影响对消性能。
目前解决交叉极化干扰问题,大部分文献是基于自适应算法或均衡理论来完成对消的。本文提出了基于复数的FastICA 方法来解决交叉极化干扰对消问题,该方法不需要掌握信号的先验知识,在基带解调前就可以实现对交叉极化干扰信号进行分离,仿真实验验证了该方法的有效性。
1 系统模型
在卫星通信系统中,为了提高传输速率同时不增加带宽,工程上较多使用极化复用技术。本文中使用线极化方式(水平极化和垂直极化两种)。将传输的基带信号经调制以后,分别送到两个极化天线上进行传输,此时发送端的两个信号分别记为sn和gn,彼此互不相关,整个系统传输模型如图1所示。
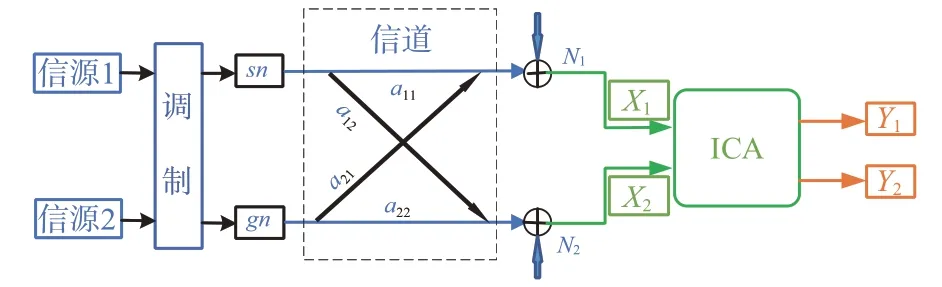
图1 系统传输模型
接收端的N1,N2为高斯白噪声,由此可以得到系统传输模型
2 复数FastICA干扰对消算法
2.1 复数FastICA算法
工程实际中,混合矩阵A的元素是未知的,可以处理的数据只有X,这类似于盲源分离问题。盲源分离的主要任务是从观测数据中恢复出感兴趣的信号,这与本论文所讨论的交叉极化干扰对消问题极为相似,所以按这个思路来解决交叉极化干扰问题。盲源分离一般模型如图2所示,在本文中白化这一过程是必要的,这是对数据的预处理环节。
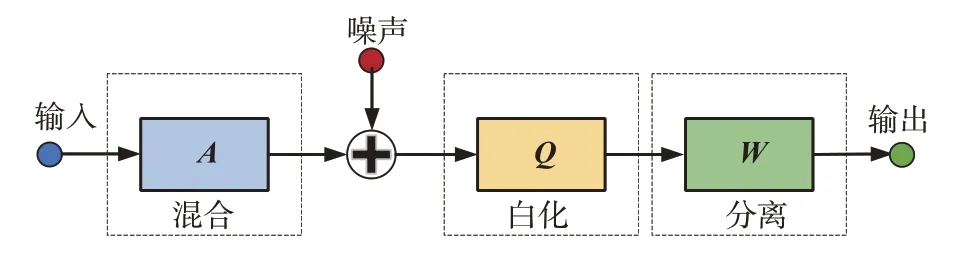
图2 盲源分离一般模型
盲源分离是依据一定的先验信息或相关理论构造目标函数的无监督学习方法,本文所使用的复数FastICA 方法就是其中一种。根据中心极限定理,基于ICA的盲源分离算法的独立性判据可以用非高斯性来度量。常用的非高斯性度量有峰度和负熵,本文使用负熵作为非高斯性度量。文献[11]基于负熵理论提出了一种稳健的、速度更快的方法来分离复信号:
w是一个n维复权向量且满足为非线性函数,X为白化后的信号且满足代表的是对一个独立成分的估计。只有当目标函数值是实数时,目标函数才能找到极值。将n个目标函数的和最大化并考虑不相关的约束条件,可以得到
式中,*为复共轭运算符。通常来说,函数G的选择对复数FastICA 算法的稳定性有着重要的影响,在这里本文选择修正的Tukey 函数为非线性函数[12],其函数表达式为
式中,a取值为分别为的一、二阶导数。之后,指定在的约束下计算复数FastICA 目标函数的最大值。这可以使用拉格朗日乘子法来求解,β为拉格朗日乘子,即
采用牛顿迭代算法对式(7)进行求解,得到关于w的迭代公式
两边同时乘以分式的分母,进一步可以得到w的迭代公式
此外,在每次迭代完成后还需要对w进行归一化处理即
2.2 算法步骤及改进
在仿真过程中需要对数据进行白化预处理。首先对采样得到的数据X先进行中心化处理,结果满足E(X)=0;然后再对数据作相关运算得到协方差矩阵R。对于白化矩阵Q,通常由混合信号相关矩阵的特征值分解来得到。混合信号X的相关矩阵R其特征值分解为
式中Λ为对角矩阵,其元素为相关矩阵的特征值,正交矩阵V的列向量为相应特征值对应的标准正交矢量。因而可以得到白化矩阵
令Z=QX,则有
即经过白化处理后的信号Z的各成分之间不相关。算法输入为白化矩阵Z=(z1,z2,…,zn),输出为独立成分Y=(y1,y2,…,yn)。算法具体步骤如下:
步骤1:迭代变量k=0,初始化权值向量w0;
步骤2:k=k+ 1;
步骤3:对w进行迭代调整
步骤5:如果算法没有收敛,则转到步骤3 重新迭代。若满足,则算法收敛;
结合本文中信道的对称特性,求出的w1满足在求w2时,在两个条件的约束下可得出的w2取值,无需重新迭代计算求解。所以使用复数FastICA 算法估计出的一个w就可以作为最终的W取值的参考,而无需迭代求解第二个权向量w,从这一角度看简化了算法运算量。
3 仿真分析
3.1 仿真参数设定
仿真中,随机生成两组符号数为5 000 的源信号,调制方式为QPSK。在混合矩阵A的设定上,α分别取10-5/20,10-10/20,10-15/20,β设定为,相应XPD 的取值则为5,10 和15 dB。根据源信号的功率,接收端对交叉极化后的信号添加高斯白噪声,算法收敛参数ε设定为10-9。
3.2 相关指标
SINR 为信干噪比,表示信号功率与干扰和噪声功率的比值。EVM 为误差向量幅度,定义为平均误差矢量信号功率与平均参考信号功率之比的均方根值,是衡量调制精度的指标[13]。PI 为性能指数,是从盲源分离的角度来分析分离前后的性能。PI 是一个用分离矩阵WHQ和混合矩阵A的乘积G与排列矩阵之间的差别来描述算法分离效果的指标。G又称为全局传输矩阵[14]。
PI值越趋于0,表明分离效果越好。在实际分离效果计算中,当PI 值达到10-2数量级时,认为已经获得了比较理想的分离效果[14]。
3.3 仿真结果
第1 组仿真XPD 取5,10 和15 dB,接收端SNR设定为10~20 dB,步长为0.5 dB,EVM 值在仿真过程中用dB表示,变化前后都为负值,仿真结果如图3 所示。图3 中,EVM 分离后要比分离前更小,随着接收端SNR 的增加EVM 值改善明显,在SNR 为15 dB 时,3 种极化隔离度下的EVM 有6.2,5.0 和2.7 dB 的改善;图4中,XPD 在分离后大都处在35~45 dB 左右,相较分离前都有20 dB 以上的提升空间。图5 中,SNR 为20 dB,XPD 取5,10 和15 dB 的情况下,分离前后的SINR 为4.9 和14.1 dB,9.5 和18.4 dB,13.7 和19.5 dB,也可以从图中看出,XPD在取值较小时算法的分离性能受SNR 影响较大。图6 中的PI 值随着SNR 的增大而趋于0.01 性能边界,说明该方法分离效果较好。
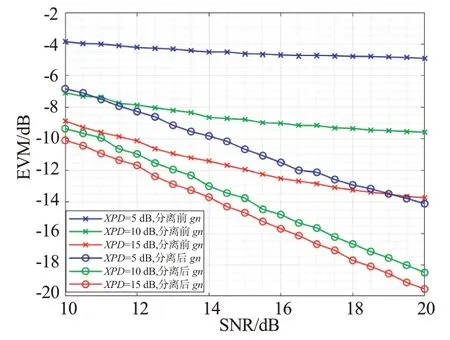
图3 分离前后信号EVM的变化
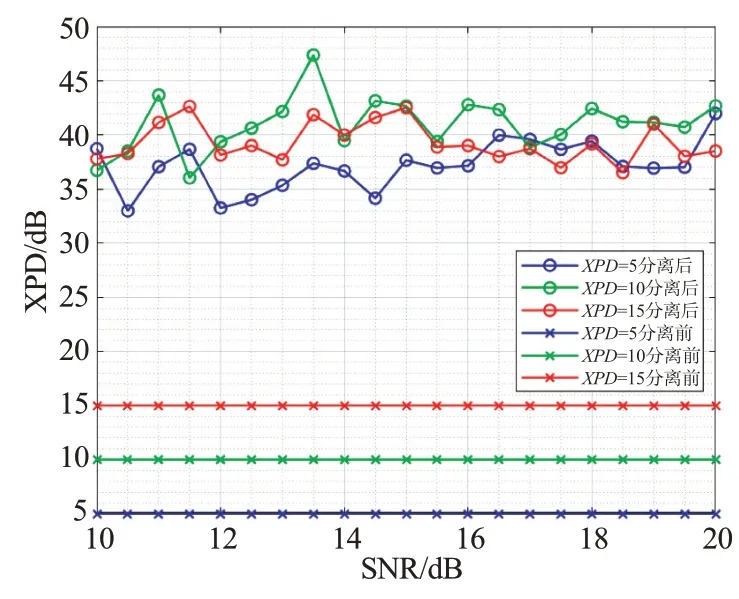
图4 分离前后信号XPD的改善
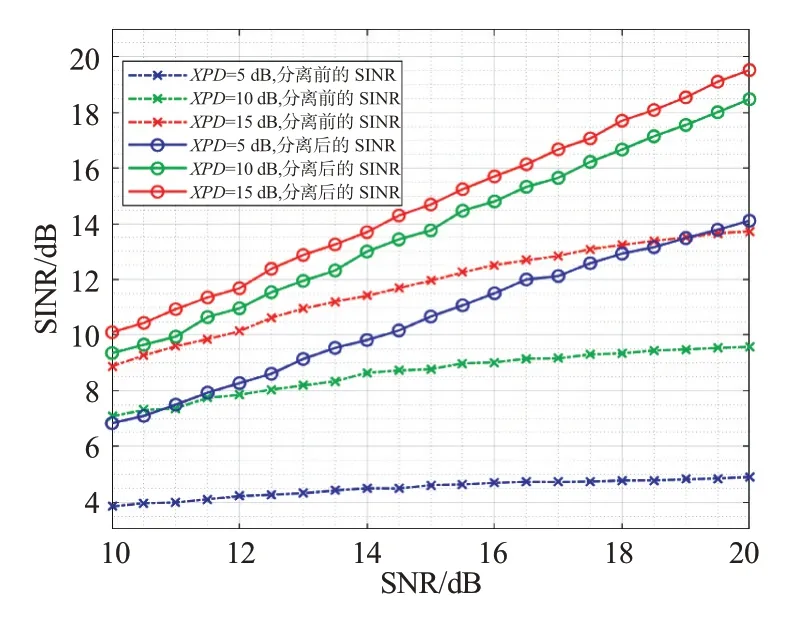
图5 分离前后信号SINR值的变化
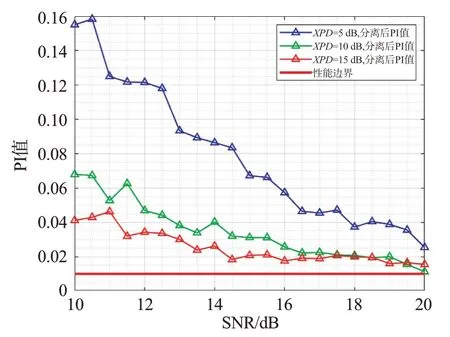
图6 信号分离后PI值渐进情况
第2组仿真是在SNR为12 dB,XPD为5,10 dB条件下,观察分离前后的星座图变化情况,如图7和图8所示,分离后星座图上的点较分离前更加集中收缩,图7分离前SINR为4.2 dB,分离后为8.2 dB,提升了4 dB;图8分离前SINR为7.8 dB,分离后为10.9 dB,提升了3.1 dB。
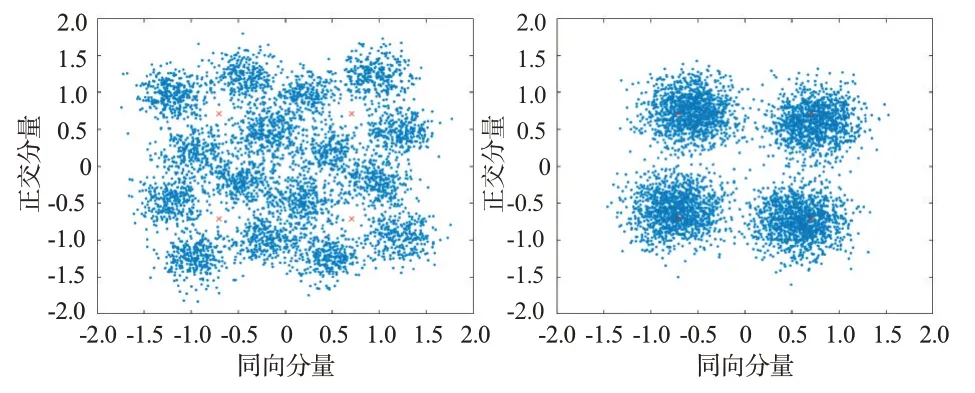
图7 XPD为5 dB时信号分离前后星座图
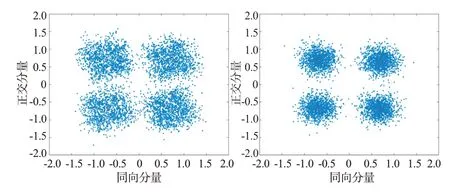
图8 XPD为10 dB时信号分离前后星座图
第3 组仿真取109个符号,信噪比取0~20 dB(步进1 dB),XPD 取5,10,15 dB 时画出的分离前后的误码性能曲线图如图9 所示。从图中可以看到,误码率达到10-4情况下,XPD 为10 dB 对消前需要的信噪比为15.4 dB,对消后为12.9 dB,算法可使得性能有2.5 dB 的提升;XPD 为15 dB 对消前需要的信噪比为13.2 dB,而对消后为12.1 dB,算法可使得性能有1.1 dB的提升。
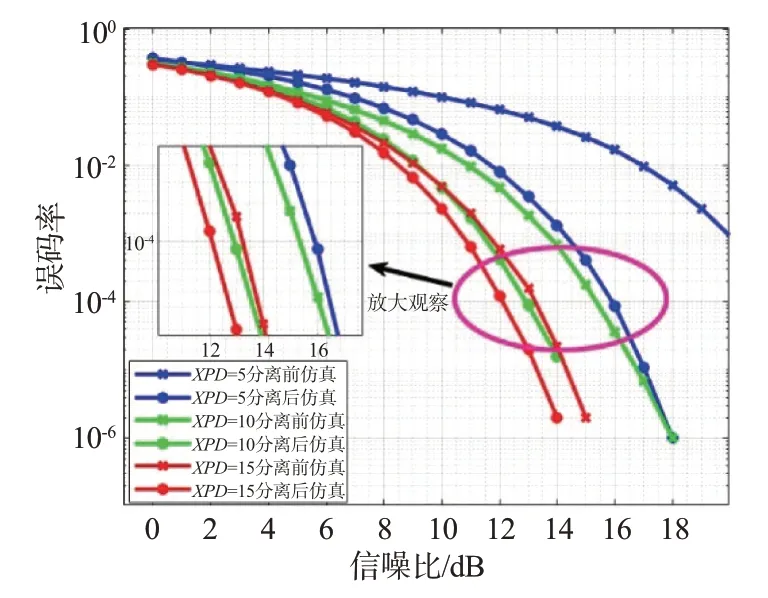
图9 QPSK误码性能分析
综合3 组仿真结果,可以验证基于复数Fast-ICA 方法能够较好解决交叉极化干扰问题,在EVM,XPD,SINR 和PI 这4 个指标上分离前后有明显提升,星座图和误码率曲线也作了补充验证。另外也可以发现,基于复数FastICA 方法在低信噪比情况下也可实现交叉极化干扰对消。
4 结束语
本文提出了可以对复信号分离的FastICA 方法来解决卫星通信中极化复用技术而导致的交叉极化干扰问题,该方法能够在不掌握信号先验信息的情况下实现交叉极化干扰的消除。根据传输信道对称的特性,简化了复数FastICA 算法来实现对QPSK 调制信号混合后的分离。从EVM,SINR,XPD,PI 和星座图这几个角度进行仿真分析,结果显示XPD 有20 dB以上的提升,PI指标趋近于理想情况,验证了该方法适用于解决交叉极化干扰问题。考虑到FastICA 算法迭代速度快但对初始权值矢量敏感这一问题,下一步我们将考虑改进算法迭代,解决鲁棒性这一问题。
