基于粒子群变权的公安智能化发展水平评价方法＊

2023-12-18王昊鹏王鹏周业勤王慧

警察技术 2023年6期

王昊鹏王鹏周业勤王慧

1.山东警察学院山东省网络空间安全大数据发展创新实验室 2.山东省滨州市公安局 3.山东省济南市公安局历下区分局

引言

党的十八届三中全会首次提出“推进国家治理体系和治理能力现代化”[1]，在数字时代，基于数据的智慧治理上升为国家战略，各级政府和各行各业都开展了数据智能化建设和应用。2019年5月7日，习近平总书记在全国公安工作会议上指出“要把大数据作为推动公安工作创新发展的大引擎、培育战斗力生成新的增长点”。各级各地公安机关围绕智慧公安建设，在顶层设计、资金投入、资源整合、信息共享、业务协同等方面做了大量工作，取得了一定的成绩[2～5]。然而各地公安智能化建设发展水平参差不齐，为提高智能化建设的针对性和有效性，对公安智能化发展水平进行评估成为亟待解决的问题。

目前对公安智能化发展水平评价的研究取得了一定的成果，2017年公安部发布了《公安基础信息化建设评价指南》[6]，构建了包含6项一级指标、21项二级指标和51项评价要素的指标体系，并为每个一、二级指标分配了固定的权重。吴新娣[7]以内蒙古公安智能化建设为对象，设计了包含8个一级指标、21个二级指标和75个三级指标的指标体系，利用熵权法为各指客观的标赋予了权重。与公安部制定的指标体系相比，该指标体系增加了服务民生和新媒体建设管理两个一级指标，丰富了对智能化建设领域的评价。张苗苗[8,9]设计了包含3个一级指标、7个二级指标和21个三级指标的指标体系，使用专家主观赋值的方法为每一个指标赋予了权重。与公安部和吴新娣团队的指标体系不同的是，该指标体系只针对公安信息化应用水平进行评价，因此不包含基础建设、数据汇聚、组织管理等方面的内容。这些研究大多注重指标体系的构建，对各指标的赋权基本采用比较简单的主观或客观赋权方法，这些方法评价结果主观性较大、适用性有限[10]。针对这些问题，本文设计了一种基于粒子群变权（Variable Weight Group Evaluation-Particle Swarm Optimization Algorithm）的评价算法，以所有评价者对所有评价指标的权重为种群，以评价结果的时空相似性为判断依据，自适应调整评价者权重，兼顾主观和客观赋权优点的同时，也避免了单独使用一种赋权方法的缺陷，提高了评价结果的准确性和稳定性。

一、公安智能化发展水平评价指标体系构建

公安部《公安基础信息化建设评价指南》是目前正在使用的标准。该指南评价对象是公安的信息化建设而不是智能化建设，虽然智能化起源于信息化，但智能化建设比信息化建设层次更深、范围更广，更注重应用的成效，因此不能直接将信息化建设评价套用在智能化建设评价中。在坚持系统性、导向性、针对性、动态性和可操作性的基础上，结合现有公安信息化建设应用水平评价指标体系，构建公安智能化发展水平评价指标体系。

该指标体系包含基础建设、数据资源、安全防护、组织管理、应用成效和科技创新等6项一级指标、基础网络建设等41项二级指标和146项评价要素（受篇幅限制不再罗列）。指标体系中既有定量指标，也有定性指标。在为指标赋值时，对定量指标，直接根据指标的实际值赋值；对定性指标采取间接赋值法[11]赋值，即先列出定性指标所有可能的取值集合，采用某种标准对“定性变量取值集合”中的元素进行赋值。本文对所有定性指标进行五等级赋值。为方便后续的评价，还应对指标进行归一化处理，即将所有指标的取值归一化到[0，1]内。

二、基于粒子群变权的评价模型

（一）评价者权重设置方法

综合评价的结果取决于被评价对象的认识。为了使评价结果更客观公正，往往以多个评价者的共同评价结论作为最终评价结果。为避免评价者之间互相干扰，每个评价者都独立评价并形成各自的评价意见，将所有评价者的评价意见通过某种规则加权汇总为最终评价结果。该结果是否客观公正取决于多个评价者的权重分配是否合理[12]。

综合评价的本质是评价者与评价对象之间随时空变化的互相交互、互相认知的过程。从评价值取得的时间上来看，一方面评价对象会随着时间的推移不断变化发展，评价者对评价对象的认识也会随着时间和评价对象的发展产生变化，而且这种变化往往滞后于评价对象的变化，用固定的评价者权重衡量发展变化的评价对象必然会影响评价结果的准确性；另一方面同一评价者对多个评价对象评价时，在时间上必然有一个先后顺序，评价尺度受评价者自身认知、心理状态和外界干扰的变化影响很难保持完全一致，固定的评价者权重会影响评价结果的一致性。从评价对象的评价值空间上来看，不同评价者对同一评价对象的评价结果应该是相似的，如果某一个评价者的评价结果与评价者群体评价结果差异过大，说明该评价者的评价结果不够客观，应适当减小其评价权重。当然，很多情况下评价指标体系覆盖多知识领域，例如公安智能化发展水平评价指标体系涵盖了公安学、管理学、计算机技术、通信技术、安全技术等多学科知识，很难找到一个具备所有学科知识的评价者，这时就不能以整个指标体系评价结果的相似性作为调整评价者权重的依据，而是将评价者权重以各级指标为单位进行拆分，然后根据各级指标评价结果的相似性作为调整评价者各级指标权重的依据。

（二）基于粒子群算法的评价者权重群

根据上述分析，可对评价者、评价对象、评价权重、评价值做如下定义：假设m位评价者组成评价者群组G={gi}，i=1,2,…,m；n个待评价对象组成评价对象群组O={oi}，j=1,2,…,n，其中第j个评价对象表示其在整个评价对象群组中是第j个被评价的；评价指标体系包含L级，每一级K个评价指标，则W(gi,l,k)表示为第i个评价者对评价指标体系中第l级第k个指标的评价权重；Y(gi,oj,l,k)表示为第i个评价者对第j个评价对象的第l级第k个指标的评价值。

本文将评价者对评价对象的所有层次化评价指标权重作为一个粒子群，评价开始前为每一个层次内的所有指标赋予平均权重，然后以评价者对所有评价对象的评价值的时空特征为依据，更新评价者权重，如此迭代，直至得到最优评价值或达到最大迭代次数。

（三）基于评价值时空特征的评价者权重调节

根据前文分析，评价者打分时受主客观影响，评价值表现出一定的时空特征。本文以这些时空特征为依据调整评价者权重。

以评价者对所有评价对象的评价顺序作为时间轴，同一个评价者对所有评价对象的同一个指标的评价尺度（或打分标准）应该是稳定的，不同评价对象的同一个评价指标如果完成情况相同或相似，其评价值也应该是相同或相似的，不能受评价顺序的影响，评价值越评越高或越评越低或忽高忽低。如果评价者对某一评价指标的评价值体现出了评价尺度前后不一的情况，应适当减小其在该指标上的评价权重。评价值时间特征可用指标完成情况与其评价值之间的欧式距离Qzy表示：

公式（1）中，Z(oj,l,k)为第j个评价对象第l级第k个指标的完成情况，为方便计算，Z(oj,l,k)和Y(gi,oj,l,k)都要事先归一化处理。

以所有评价对象作为空间轴，所有评价者对同一个评价对象的评价值应该是相同或者相似的，在实际评价中，评价者受自身知识结构、偏好等主客观因素影响，无法做到相同或相似。为了减小这种影响，很多研究基于单一评价者与整个评价者群体的“评价结果相似性”调整评价者权重，而对“评价结果相似性”的定义有的用平均值、有的用方差等。这些方法确实取得了较好的效果，但其只从评价结果这个表面现象上消除了不一致，没有从评价者自身知识结构、偏好上消除产生不一致的根源。同时，由于将评价者的权重作为一个整体，调整权重时还牺牲了一部分客观性。

为此本文将评价者权重按照评价指标体系，在空间上进行层次化打散。对评价对象的总体评价目标、一级指标、二级指标分别设置评价者权值，依据其所对应的总体评价目标、一级指标、二级指标评价结果的相似性分别调整。

对评价者群组G={gi} 中的任意评价者gi对第l级指标评价值可表示为：

任意两个评价者ge和gh对第l级指标评价值的余弦相似度表示为：

则评价值空间特征可用评价者群组G={gi}的评价相似性表示：

综合公式（1）和（4），粒子群的目标函数可表示为：

（四）基于可变滑动窗口的陷入局部最优判断

粒子群算法在处理多峰复杂问题时容易将局部小峰值误认为全局最优峰值而停止迭代，为避免陷入局部最优，本文设计一种基于可变滑动窗口的陷入局部最优判断方法。粒子群算法初始迭代前设置一个窗口尺寸为1、起始位置也为1的滑动窗口，经过一次迭代后，计算相邻两代的评价意见的相似性，若相似性较小则滑动窗口起始位置更新为当前代，同时窗口尺寸减为1；若相似性较大则首先判断滑动窗口尺寸，若小于3则滑动窗口位置不变，尺寸加1，若大于等于3则认为陷入局部最优，同时将滑动窗口起始位置更新为当前代，并将尺寸减为1。具体流程如图1所示。

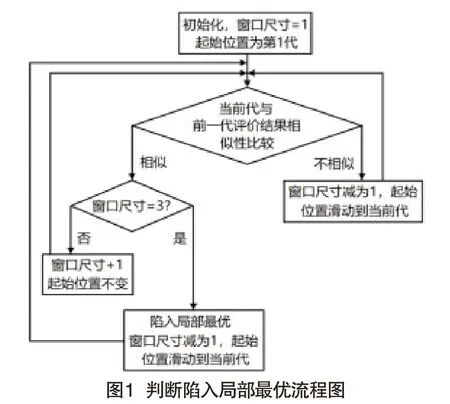
混沌算法具有在其取值范围内不重复遍历的特征，因此常被用于跳出局部最优。本文使用混沌算法跳出局部最优，当判断算法陷入局部最优后，在下次迭代时使用混沌算法的Logistic映射重新构造粒子种群。

（五）基于评价者权重波动的惯性系数更新

粒子群算法中的惯性系数ω用于表示粒子维持自身速度不变的趋势，一般设定在0.4～0.9之间，既可以是固定值，也可以是变化值，ω越大代表全局搜索能力越强，ω越小代表局部搜索能力越强。在算法初始阶段为了快速找到最优解的大体位置，可以设置较大的ω值，在算法迭代后期，为了进行精确的局部搜索，可以设置较小的ω值。

对群组评价，由于评价初始阶段各评价者评价意见差异较大，为得到一致性较高的评价意见，评价者权重会产生较大变化，随着迭代次数的增加，评价意见趋于一致，评价者权重的调整幅度也会减小。这个规律正好符合惯性系数ω变化规律，因此，可用评价者权重波动表示惯性系数。假设当前迭代次数为t+1，则所有评价者对各级指标总的权重波动可表示为：

根据公式（6）可知权重波动范围区间是[0,1]，将其映射到惯性系数ω的[0.4,0.9]取值范围，则惯性系数可表示为：

（六）改进算法描述

综合第二章（一）～（四）部分内容，可将本文提出的基于粒子群变权评价算法（VPSO）步骤描述如下：

1.初始化

对粒子群算法进行初始化，评价者初始权重赋平均值，设置算法最大进化代数M，惯性系数ω，加速系数c1和c2。

2.更新

使用公式（6）计算权重波动，使用公式（7）计算权重系数。

3.评价

使用公式（5）对评价结果相似性进行评价，记录粒子的历史最优位置和种群的历史最优位置。使用滑动可变窗口算法判断是否陷入局部最优。若陷入局部最优则继续执行本步骤，否则转到下一步骤。

4.跳出局部最优

使用混沌算法，重新构造种群并转到第2步骤。

5.结束

判断是否达到最大进化代数或满足结束条件，若满足则算法结束，否则转到第2个步骤。

三、算法验证

（一）实验数据

自2021年9月开始，对我国东部沿海A省的15个地级市进行了历时9个月的调研及数据采集。以该数据为依据，邀请公安智能化系统设计人员、公安机关信通部门管理人员、公安机关各类智能化系统使用人员和高校及科研院所公安智能化应用研究人员等四类共20人进行评价，使用评价结果对本文设计的算法进行验证。

（二）实例验证

为验证本文提出的算法，分别使用标准AHP法（文献8使用的方法）、标准熵权法（Entropy Method，文献7使用的方法）、标准粒子群算法（PSO）和本文提出的算法（VPSO）对本文设计的指标体系和第三章（一）部分中的数据进行指标赋权及评价打分，41个二级指标，每个二级指标满分10分。

使用标准AHP法时，首先请20位评价者分别根据指标体系对各一级、二级指标赋权并根据第三章（一）部分的数据对各指标打分，然后对20位评价者的赋权进行算数平均，用平均权值分别与20位评价者的评价值计算各评价对象总评价值，最后计算20个总评价值的算数平均值，作为最终评价结果。

使用标准熵权法时，首先根据本文的指标体系和第三章（一）部分的数据，用熵权计算公式计算各一级、二级指标权重，然后用熵权权重分别与20位评价者的评价值计算各评价对象总评价值，最后计算20个总评价值的算数平均值，作为最终评价结果。

使用粒子群算法时，算法各参数设置如下：将每一位评价者对指标体系中每一个一级、二级指标的评价权重视为一个粒子，最大进化代数T=200，使用公式（5）作为目标函数，r1和r2设为[0,1]之间的随机数，加速系数c1和c2用于平衡粒子自身最优和种群整体最优，表示形式为：

式中，cmax和cmin分别取2.0和0.5，t和tmax为当前迭代次数和最大迭代次数。

标准粒子群算法种群规模N=20，使用固定惯性系数，不判定是否陷入局部最优；本文算法种群规模N=980，使用公式（7）确定的可变惯性系数，使用可变滑动窗口思想判定是否陷入局部最优并使用混沌算法跳出局部最优。

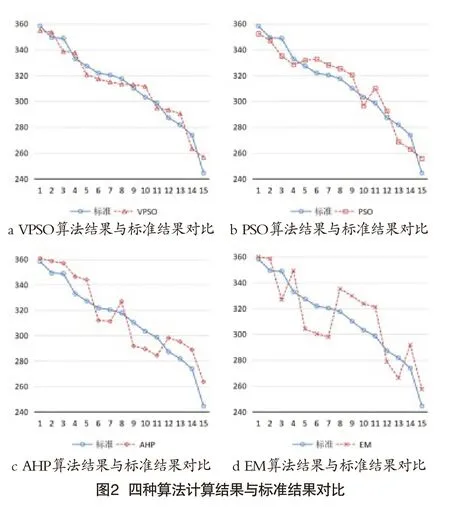
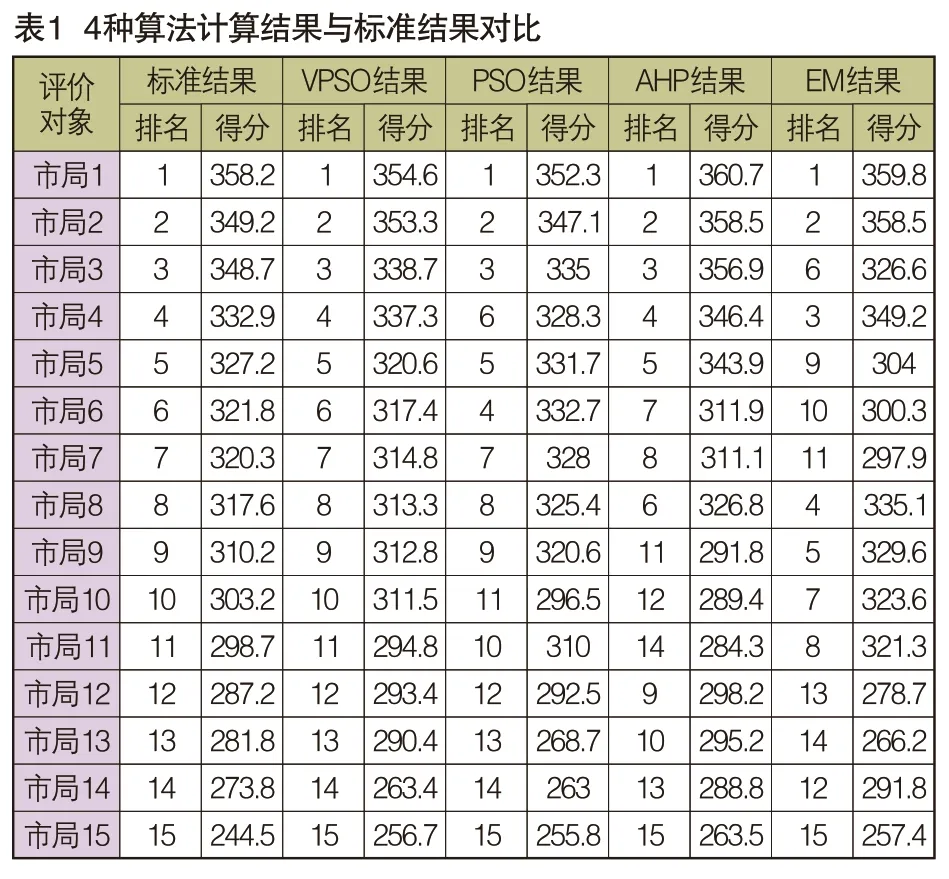
各算法计算结果与标准结果（该标准结果为2021年A省15个地市公安智能化发展水平评价官方公布结果）对比如图2、表1所示。

使用得分相似度和排名相似度来衡量各算法评价结果的准确性，可分别表示为：

式中，Simscore和 Simrank分别表示得分相似度和排名相似度，分别表示不同算法计算的总分、标准总分、不同算法计算的排名和标准排名。根据表1计算得到各相似性结果详见表2。

表2 各算法得分相似度和排名相似度

从表1、表2和图2可以看出，VPSO算法得到的排名与标准排名完全一致，PSO算法、AHP算法和EM算法得到的排名与标准排名分别有4个、9个和12个评价对象顺序不同，四种算法排名相似度分别为100%、73.33%、40%和40%，得分相似度分别为97.89%、97.23%、95.94%和94.57%。虽然VPSO算法得到的各评价对象的评价值与标准结果不完全一样，但基本与标准结果曲线重合，说明VPSO算法的各评价值与标准结果基本一致，而其他三种的评价值与标准结果差异较大。

VPSO算法得到的各一级指标排名与各一级指标的标准排名完全一致，说明VPSO算法对同一个评价者评价不同指标赋予不同权重，既保证了总结果的准确性，也保证了各指标评价结果的准确性。PSO算法、AHP算法和EM算法对各一级指标评价结果与标准结果差异很大，这是由于三种算法对同一个评价者评价不同指标赋予相同权重，无法保证各指标评价的准确性。综上所述，本文提出的VPSO算法可同时对公安智能化总的发展水平和各指标的发展水平进行精确有效的评价。