面向机器视觉任务的多尺度图像特征压缩算法
2023-12-18张云飞贺丽君王子溪李凡
张云飞, 贺丽君, 王子溪, 李凡
(西安交通大学电子与信息学部, 710049, 西安)
近年来,随着深度神经网络(deep neural networks, DNN)的发展,庞大的计算量和显存开销等问题日益凸显。当前边缘设备应用DNN的常见算法是将数据传输到云端执行视觉任务,但纯云端的数据传输方式延时大,通信开销高。Kang等[1]提出了协作智能(collaborative intelligence, CI)框架,将DNN的前半段放在边缘端,传输中间特征到云端完成推理任务,实现了边缘设备和云端的负载均衡[2]。由于中间特征扩展了图像的维度,造成数据量较大,因此,特征的压缩传输效率是影响CI框架性能的关键因素。机器视觉编码(video coding for machine, VCM)[3]技术应运而生,该编码技术致力于弥合视觉特征压缩与经典视频编码之间的鸿沟,将视觉特征作为桥梁,以可扩展方式连接信号级和任务级的紧凑表示[4]。由于难点在于现有的编码器主要面向图像、视频设计,因此,将其应用于中间特征编码并不高效。此外,由于中间特征具有稀疏的数据分布,增强中间特征的紧凑性也是提高应用效率的关键。
目前,已有的特征压缩算法可分为编码压缩、空间压缩、特征优化和多尺度特征压缩4类。编码压缩利用传统或非传统的编码器将特征量化,消除统计冗余后编码为二进制码流。元辉等[5]提出基于局部亮度补偿的视频编码算法,提高了视频的编码效率。类比可知,特征也能去除冗余信息,从而进行压缩传输。汪维等[6]对残差网络(ResNet)[7]各层输出开展了有损编码与无损编码的对比实验,证明无损压缩效率较低。Choi等[8]研究了基于高效视频编码(HEVC)[9]的特征编解码方案,对每个通道的特征图进行量化处理,使用HEVC编码器将特征编码进行传输。Suzuki等[10]研究了中间特征各通道之间的伪时间关联性,通过对特征进行时空排列,使用视频编码器完成了编码传输。然而,上述研究仅通过量化编码去除统计冗余,并没有考虑特征的空间冗余。
空间压缩从特征本身的稀疏性出发,通过调整特征的空间尺寸进一步压缩特征数据量。Eshratifar等[11]提出了一种名为瓶颈单元的可学习压缩单元和有损压缩感知训练算法,分别在ResNet-50和VGG-19[12]网络上实现了特征压缩。Ikusan等[13]考虑特征之间的相似性,设计了分层聚类特征选择策略。由于上述算法依然采用传统编码器对紧凑特征编码进行传输,码流中仍存在较多的统计冗余。
通过可训练的编码模块,特征优化能够将特征压缩与参考网络联合优化。宋蓓蓓等[14]提出了结合码率预测和率失真优化的码率控制算法,实现了对图像码率的高精度控制。Alvar等[15]设计了一个损失函数衡量特征的压缩特性,用来约束模型的训练过程。Chamain等[16]利用压缩模块和任务算法组成链路,联合微调编解码器和任务网络显著提高了任务精度。然而,端到端的训练令压缩传输的特征与任务强相关,限制了特征的泛化能力。
多尺度特征压缩是适用于复杂网络的特征压缩算法。为了保证对多尺寸目标的检测效果,主流的检测、分割网络如Faster RCNN[17]、YOLO[18]、Mask RCNN[19]等,需要在主干网络中引出多条支路分别完成推理任务。Liu等[20]提出将图像转换为多个子带的金字塔,通过对变换模块进行训练,发现特征对多种机器视觉任务有用。Zhang等[21]提出了一种端到端的多尺度特征压缩框架,将多尺度特征融合为单尺度特征进行编码传输。但是,以上这些算法既没有探索不同尺度特征之间的关联,也没有针对中间特征进行编码优化。
为了实现多尺度特征的高效压缩传输,本文对比了不同尺度特征的轮廓和细节,发现多尺度特征之间存在着强相关性,可以通过残差变换去除相关性,然后使用预测重建的方式恢复特征,消除传输过程的空间冗余,同时采用自编码器消除传输过程的统计冗余。在此基础上,提出了一种基于残差变换模块、自编码器和预测重建模块联合优化的多尺度特征压缩算法。首先,设计了预测重建模块,将多尺度特征逐层作差压缩为紧凑特征;其次,采用面向特征的自编码器,将紧凑特征编码传输;然后,设计预测重建模块,将预测特征和重建的残差特征相结合,实现了多尺度特征的精确重建,并采用3个可训练的算法模块,使用码流与保真度构建损失函数进行联合优化;最后,通过仿真实验对比了多个特征压缩算法码率-精度的性能,证明了本文算法的优越性。
1 多尺度特征联合压缩算法
1.1 算法总述
本文以Faster RCNN作为骨干网络,提出了一种多尺度特征联合压缩算法,算法总览如图1所示。该算法由残差变换模块、面向特征的自编解码器和预测重建模块3部分组成,通过3个模块的联合优化,不仅实现了多尺度特征的融合压缩编码,还降低了VCM算法的传输延时与能耗,提高了协作智能的应用效率。
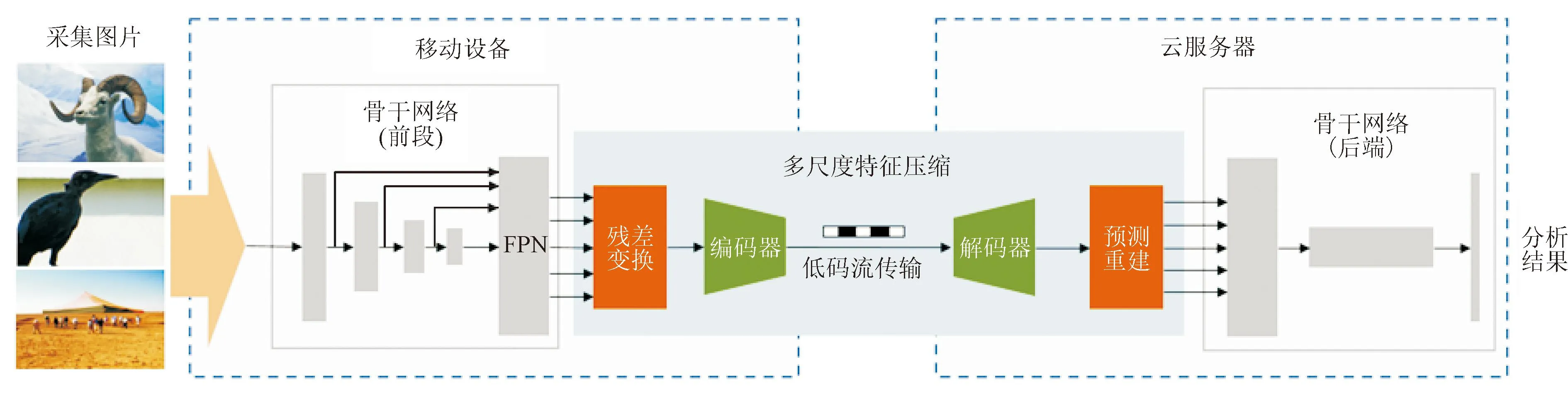
图1 面向多尺度特征的联合压缩算法总览
残差变换模块和自编码器部署在边缘设备,解码器和预测重建模块部署在云端。在边缘端使用骨干网络的前端提取多尺度特征,采用残差变换模块消除多尺度特征的相关性,并转化为统一尺寸的规范特征,然后使用自编码器编码为比特流上传到云服务器。解码器对接收到的数据进行解码处理,经过预测重建模块完成多尺度特征的高质量恢复,最后通过骨干网络的后端完成推理任务。
1.2 残差变换模块
在设计多尺度特征压缩模块之前,先探索了不同尺度特征之间的关联性。提取Faster RCNN网络模型中特征金字塔(feature pyramid network, FPN)的不同尺寸特征p2、p3、p4、p5、p6,其中p6由p5通过池化操作获得,由于不包含p5以外的信息,所以在进行特征压缩研究时不予考虑。图2给出了经过伪彩图处理的p2、p3、p4、p5层特征的可视化结果。
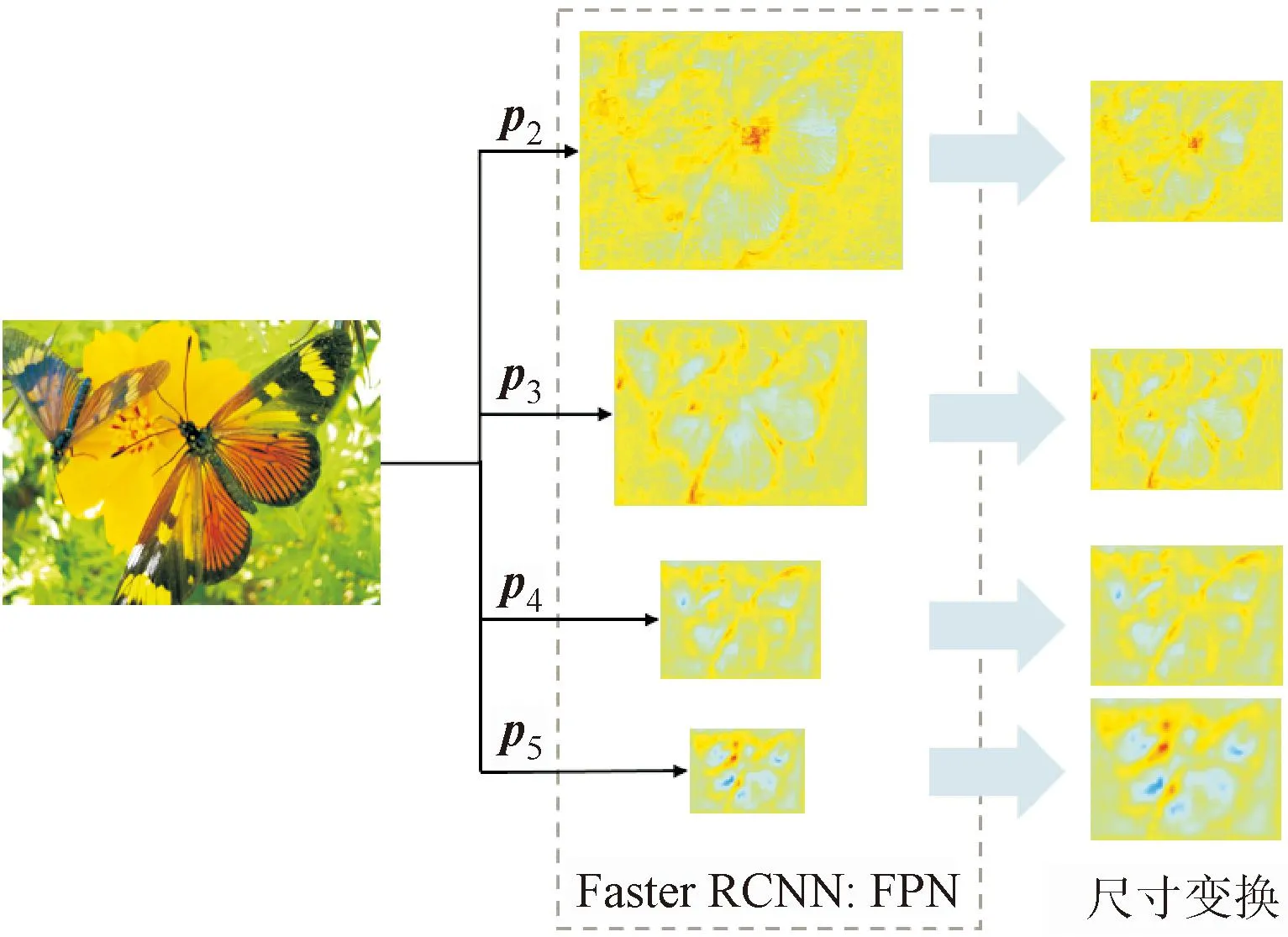
图2 Faster RCNN网络模型中多尺度特征可视化结果
统一尺寸后发现,不同层的特征具有相似的轮廓,即多尺度特征之间存在明显的相关性。若将这种相关性应用于特征压缩中,可以极大地节省中间特征压缩传输的数据量。但是,不同尺度特征之间的细节差异也不能忽略,因为这些细节信息赋予了DNN网络对多尺度物体的辨识能力。因此,本文设计了针对多尺度特征的差异信息进行压缩编码的残差变换模块,在保留不同特征差异信息的同时,通过残差处理高效压缩多尺度特征。
多尺度特征在空间上呈现为金字塔结构,可通过逐层作差的方式消除层级相关性。文献 [21]的实验结果表明,p5层对冻结模型推理的影响程度最大。因此在进行残差计算时,以p5层作为基本特征,后续处理只进行数值变换。值得注意的是,不同特征的空间尺寸、数据分布都不相同,不能直接进行残差计算,而是需要加入反卷积层[22]充当空间变换的桥梁,从而扩展低级特征的尺寸。残差变换模块的具体网络结构见图3,其中f2、f3、f4、f5分别表示被压缩的p2、p3、p4、p5层的残差特征,f表示残差变换模块输出的统一格式的单尺度特征,k、s、c分别表示卷积层和反卷积层的尺寸、步长和输出通道数。

图3 残差变换模块的网络结构
该模块由卷积层、残差块、反卷积层和通道拼接操作组成,根据多尺度特征的金字塔特性,逐层作差消除不同尺寸特征的相关信息,然后对残差特征进行空间变换,与p5的尺寸保持一致。与此同时,对p5特征采用尺寸为3×3的卷积进行数值变换,尽量消除与残差特征数值分布上的差异。最后对所有特征按通道进行拼接,经过卷积层与残差块的处理,输出具有统一格式的单尺度特征。压缩过程可表示为
f5=trans(p5)
(1)
f4=trans(p4-sizeAlign(p5,p4))
(2)
f3=trans(p3-sizeAlign(p4,p3))
(3)
f2=trans(p2-sizeAlign(p3,p2))
(4)
f=trans(concat(f5,f4,f3,f2)
(5)
式中:trans(·)操作为对残差特征进行尺寸变换和数值变换;sizeAlign(a,b)操作为将张量a的空间尺寸变换到和张量b一致;concat(·)操作为将特征按照通道进行拼接。
残差块是由主分支和快捷连接组成的双分支结构,输入输出均为特征图。主分支由两个尺寸为3×3的卷积和广义分裂归一化(GDN)层[23]构成,第一个卷积步长设置为2,在完成输入特征空间尺寸的变换后,采用GDN层代替批归一化(BN)层,以便后续多尺度特征的重建。快捷连接限制输入特征的内容损失,使用尺寸为1×1的卷积实现两条支路输出特征空间尺寸的匹配。上述具体结构见图4,其中,C为输入特征图的通道数目,H为特征高度,W为特征宽度。
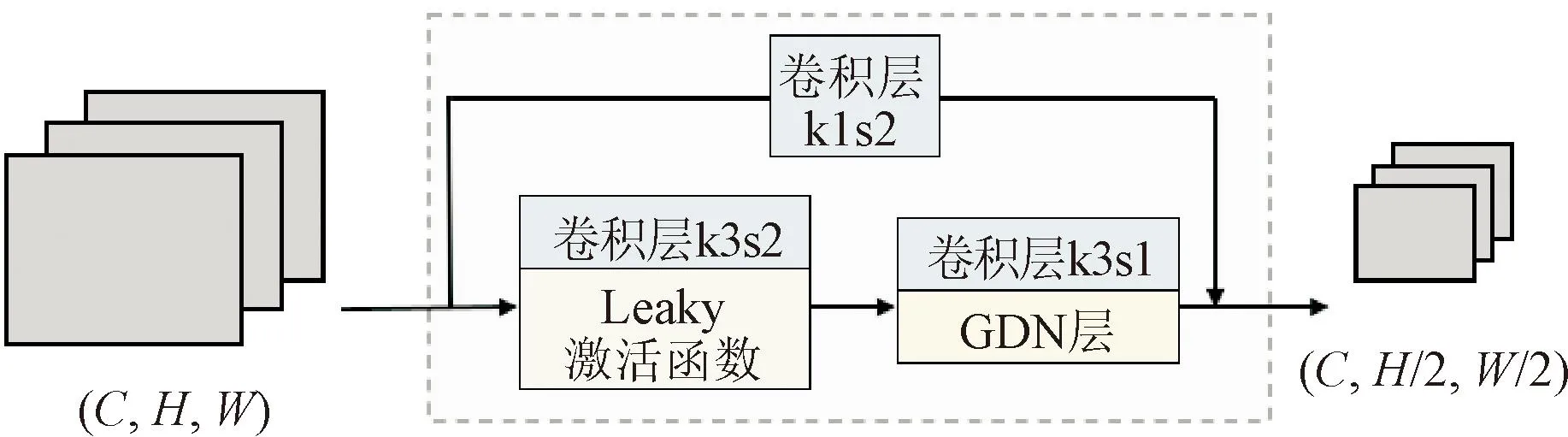
图4 残差块的基本结构
综上所述,残差变换模块通过消除多尺度特征之间的空间冗余,实现了对多尺度特征的高效压缩。将残差块与卷积层相组合进行特征变换,在实现残差特征压缩的同时,保留了中间特征的表达能力,让压缩后的特征在后期能够得到高质量的恢复。
1.3 面向特征的自编码器
近年来,深度图像编码算法得到深入发展。与HEVC算法相比,在相同的码率下,最新的Cheng2020算法[24]获得的图片重建性能更高。此算法通过深度编码器扩展图片特征空间,经过量化编码传输,采用对称的孪生网络重建图片,其本质为特征的压缩传输。残差变换模块输出的特征已经过压缩处理,能够较方便地进行编码传输,之后再通过对称的解码结构生成重建特征。自编码器的网格结构见图5,其中,f表示残差变换模块输出的压缩特征,f′表示自编码器的重建特征。
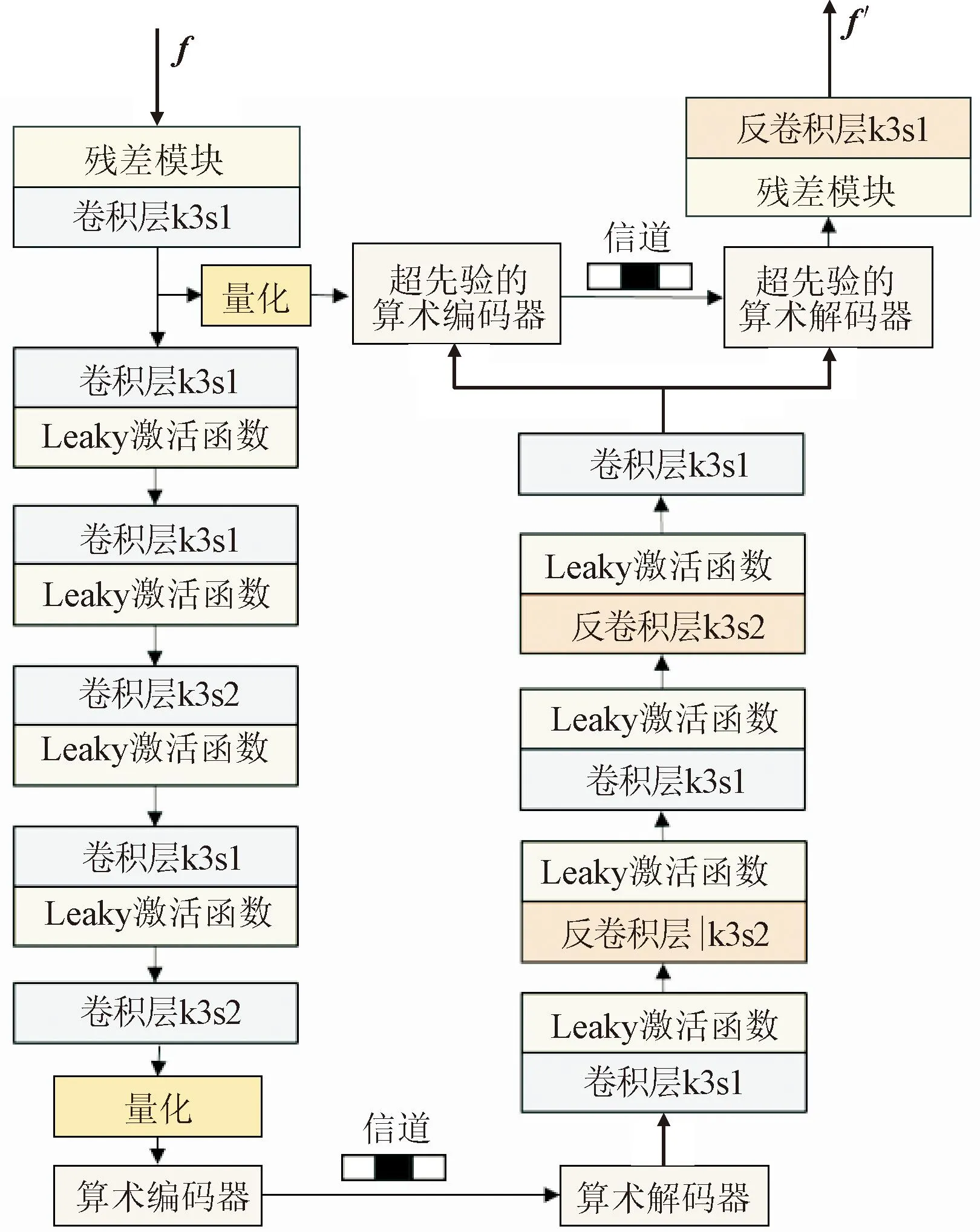
图5 面向特征的自编码器网络结构
由骨干网络前端提取到的该模块输入的中间特征,经过残差变换模块的压缩已经能满足紧凑性的要求,不需要进一步再压缩。对于超先验编码器,该模块输入的压缩特征尺寸较小,最多能进行两次下采样,否则包含的信息不足以指导算术编码器。解码器的目标是最大程度地还原压缩信息,所以采用对称设计。此时,使用逆函数iGDN层替代解码器的GDN层,将下采样的卷积层改为上采样的反卷积层,并对称设计输入、输出的通道数。
采用面向特征的自编码器去除编码冗余,可实现特征的高效编码。该模块是可训练的,与残差变换模块进行联合优化,能够实现传输码率与表现力的最佳权衡。
1.4 预测重建模块
根据多尺度特征之间的相关性,该模块采用逐层预测方式,精确重建多尺度中间特征p′2、p′3、p′4、p′5、p′6。残差变换模块底层特征p5压缩程度最小,信息保存最为完整,因此首先完成恢复。通过split(·)操作将f′按通道分割为f′5、f′4、f′3、f′2,通过f′5精确重建p′5、p′6。与此同时,p′5采用sizeAlign(·)函数预测p4的特征值,再与残差特征结合,精确恢复p4的特征p′4。每层特征的重建可表示为
(f′5,f′4,f′3,f′2)=split(trans(f′))
(6)
p′5=trans(f′5)
(7)
p′6=pooling(p′5)
(8)
p′4=trans(f′4)+sizeAlign(p′5,p4)
(9)
p′3=trans(f′3)+sizeAlign(p′4,p3)
(10)
p′2=trans(f′2)+sizeAlign(p′3,p2)
(11)
式中:split(·)操作表示将特征按照原来的通道数进行分割;pooling(·)操作表示对特征做池化处理以恢复最小层特征。
采用与残差变换模块对称的设计方式进行模块搭建,首先,通过残差层与卷积层的组合完成解码特征数值变换,便于后续特征分割;然后,对f′5进行数值变换,作为基本重建结果p′5开展逐级预测;接着,对于分割出的残差特征,使用残差块变换空间尺寸,卷积层扩展特征通道;最后,将预测特征与残差特征分别结合,以实现多尺度特征的高质量重建。该模块也使用了残差块实现中间特征空间尺寸的扩展,将第一层卷积替换为反卷积层,同时用iGDN层替换GDN层,以增强特征的重建效果。
预测重建模块是生成模型,经过与残差变换模块的对称设计,可以实现极低码率场景中对多尺度特征的恢复。下文将开展实验对此结论进行验证。
1.5 损失函数设计
完成残差变换模块、自编码器和预测重建模块的设计后,再通过联合优化的方式调整网络参数,旨在消除统计冗余。联合优化的损失函数L可以表示为
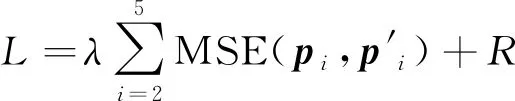
(12)
式中:MSE(pi,p′i)操作为计算pi和p′i的均方差,用于定量描述特征的压缩重建效果;R为传输比特率;λ为引入的权重参数。
由于量化编码过程不可微,不能用在训练流程中,但可进行加性高斯噪声模拟量化操作,再通过信息熵估计编码比特率R。使用比特率R消除统计冗余,会让多尺度特征变为更紧凑的表达形式,但也不可避免地导致特征表达能力的损失。此时,在损失函数中引入权重参数λ,就能实现传输码率和特征表现力的权衡。
2 仿真实验
本文在型号为NVIDIA GTX 3090 GPU、Intel(R) Xeon(R) Silver 4316 CPU 2.30 GHz的工作站上开展了仿真实验,基于深度学习框架Pytorch构建了算法模型,通过实验验证了算法的优异性能,设计消融实验证明了模块的有效性,最后将算法用于Mask RCNN网络模型的特征编解码,完成了泛用性验证。
2.1 实验设置
采用Faster RCNN为骨干网络,基于COCO预训练模型,提取FPN输出的中间特征作为压缩算法的输入,采用式(12)对残差变换模块、自编码器和预测重建模块进行联合优化。训练过程使用2个Adam优化器分别优化熵编码部分和压缩模型的其他参数,其中熵编码器的学习率固定为1×10-3,另一优化器的初始学习率设置为1×10-4,然后呈指数衰减,数据集每完整训练10次,学习率衰减为原来的1/2, 2个优化器同步进行优化,训练批次设置为16。为了获得不同压缩比的模型,权重参数λ取不同的数值。
2.2 数据集
实验使用COCO数据集[25]训练,在OpenImage数据集[26]上进行性能评估。COCO数据集是图像检测领域的经典数据集,OpenImage数据集是可商用的、规模较大且标注精确的图像检测分割数据集。
2.2.1 COCO数据集
此数据集主要从复杂场景中截取,图像中的目标通过精确分割进行位置标定。面向检测任务,训练集中有118 287张图片,测试集中有5 000张图片,各划分为80个类别。实验中,将COCO数据集中的图片输入到冻结DNN网络的前端以获取多尺度特征,用于特征压缩算法的训练优化。
2.2.2 OpenImage数据集
此数据集包含900万张训练图片、41 620张验证图片和125 456张测试图片,能够提供图像层标签以及分割掩码,可用于目标检测和语义分割任务的训练及测试。
2.3 测试流程和评估指标
通过Detection2中的检测模型Faster RCNN和分割模型Mask RCNN,对OpenImage数据集的子集进行测试。对于原始图像,使用图像编码算法(VVC)进行压缩传输,重建图像后转换成特定格式送入神经网络,得到不同机器视觉任务的推理结果。对于Faster RCNN网络模型中FPN输出的多尺度特征,采用VVC算法进行压缩传输,重建特征以完成后续机器视觉任务,得到不同任务的推理结果。最终比较时,以VVC算法压缩传输的原始图像和多尺度特征作为参考,通过码率-精度曲线证明本文算法的优越性。
对于目标检测和语义分割任务,使用传输码率和DNN网络推理精度对提出的特征编码算法进行评估。对于图像数据集,传输码率R定义为压缩码流比特数与原始图片像素数之比,以每个像素占用的比特数(bit·像素-1)作为衡量单位。
对于目标检测和语义分割,采用平均精度(mean average precision, mAP)来衡量DNN网络的性能。其中,给定阈值的召回率定义为该阈值对应的所有真正样本与假负样本中所有真正样本的比例,推理精度定义为来自所有正例与所有真正例的比例。实验中测试mAP时,阈值设置为0.5。
2.4 实验结果评估
2.4.1 特征融合与空间性能评估
对残差变换模块进行特征融合,需要完成空间压缩。因此,首先验证经过空间压缩的特征能否被精确恢复。为了进行比较,分别采用MSFC算法、Cheng2020算法和本文算法测试了特征压缩的推理精度。由于残差变换模块没有编码压缩能力,因而仅计算原始码率。
原始图像的宽、高、通道数分别定义为w、h、c,由于图像处于像素空间,c取3,因此原始图像的空间信息可以表示为(3,h,w)。由于每个元素都是uint8的非负整数,数值深度为8 bit,可知原始图像的每像素比特为24,下面分别说明各算法的空间压缩效率。对于Cheng2020算法,在骨干网络前端对图像提取特征的基础上,将输入张量的通道数与特征通道数保持一致,对特征逐个进行压缩编码,其中p2空间尺寸过大,采用采样算法将空间尺寸变为原来的一半,p2、p3、p4、p5压缩后的空间信息分别为(256,h/32,w/32)、(256,h/32,w/32)、(256,h/64,w/64)、(256,h/128,w/128)。
对于MSFC算法,多尺度特征进行了融合压缩,压缩后的融合特征表示为(64,h/32,w/32)。对于本文算法,多尺度特征进行残差处理再经过融合压缩,可表示为(192,h/64,w/64)。特征图元素均为Float32浮点数,数值深度为32 bit,计算每种算法的码率并测试DNN网络的推理精度,结果见表1。其中,特征压缩率定义为每种算法的码流与多尺度特征码率之比,用以说明各算法空间压缩的效果。

表1 不同压缩传输方法空间压缩性能对比(未编码)
从表1可以看出,DNN网络对特征的提取扩展了图片的表达空间,多尺度特征的数据量最大。3种特征压缩算法中,Cheng2020由于面向图像编解码设计,特征信息损失最多。本文算法的特征压缩比最大,但DNN网络的推理效果最好,表明本文算法重建的多尺度特征表达能力最完整。
2.4.2 特征压缩算法性能评估
本文通过计算码率-精度(rate-accuracy, RA)性能评估特征的传输效率,分别测试了VVC传输图片、VVC传输多尺度特征、Cheng2020编码、MSFC编码及本文算法编码的传输特征。对于传统编解码算法,通过调整量化参数实现对码率的控制;对于深度学习算法,可通过调整损失函数中的权重参数实现对码率的约束;对于本文算法,通过设置不同的权重参数λ={15,25,50,100,1 000,5 000},得到不同的传输码率。采用不同压缩传输算法得到的RA曲线如图6所示。
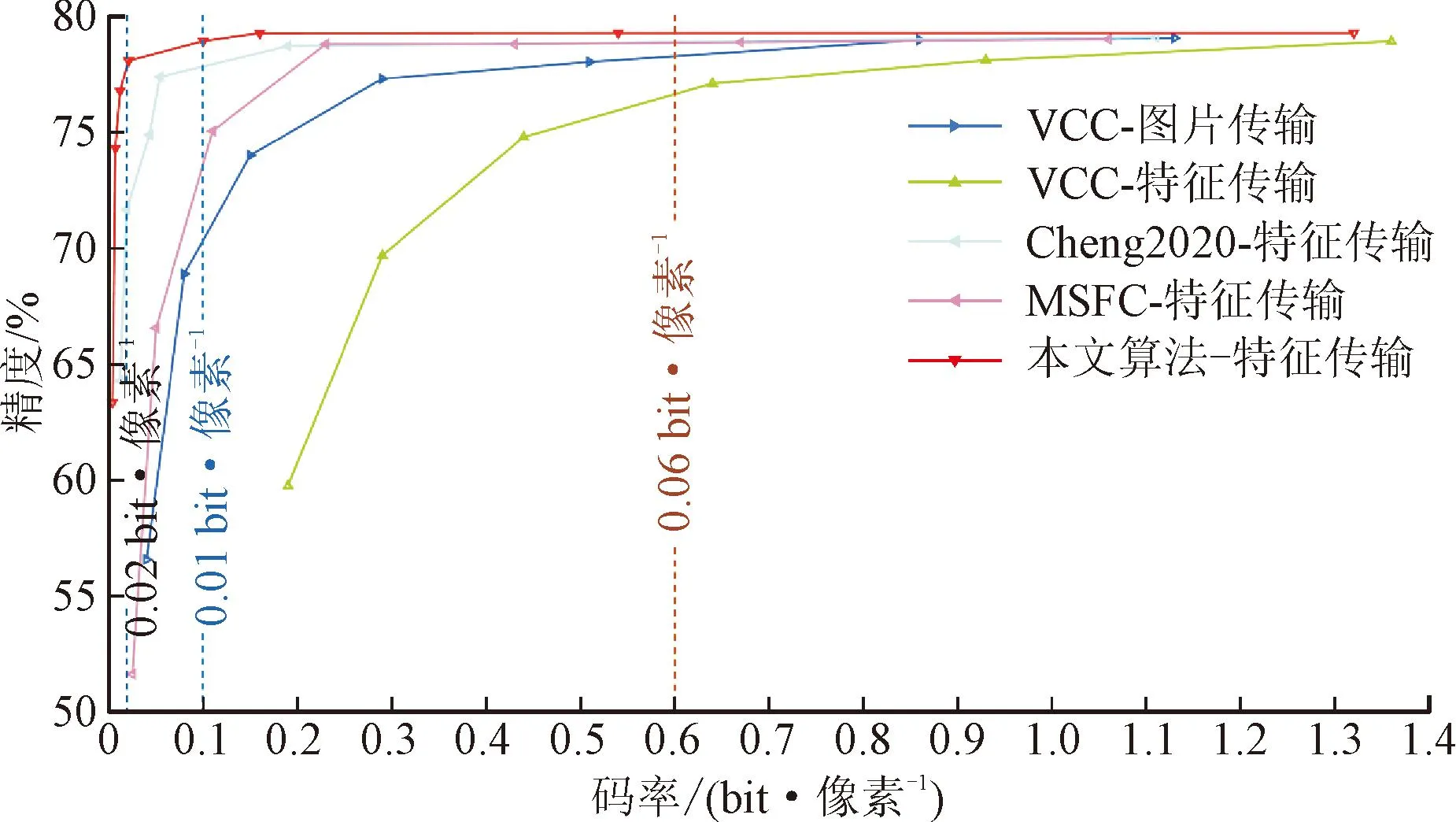
图6 不同压缩传输算法码率-精度性能对比(已编码)
由图可见,本文算法的特征压缩效果最优。在传输码率小于0.1 bit·像素-1的极低码率环境下,各种压缩传输算法均不能维持特征信息的完整性,导致推理精度急剧下降。然而,随着传输码率的降低,本文算法退化最慢,可以在极低码率下获得最优的推理性能。在传输码率约为0.02 bit·像素-1时,DNN网络的推理精度损失不超过2%,在码率为0.004 bit·像素-1时,本文算法依然能够维持63.30%的推理精度。上述结果表明,本文算法的压缩特征是有效的,能够提高VCM框架的传输效率。
为了直观地比较各种压缩传输算法的差异,将压缩特征重建并可视化。由于码率为0.1 bit·像素-1时,各算法重建特征差异最大,因而给出此码率下可视化p2层的特征,如图7所示。可以看出,VVC-图片传输和本文算法更多地保留了原始特征的轮廓信息。但VVC算法在低码率传输图片时,由于图片信息丢失,导致中间特征的数值分布和原始图像特征存在较大差异,推理效果并不理想。而本文算法在保留特征轮廓信息的同时,以MSE函数作为约束,尽可能在细节上与原始特征保持一致,因此特征重建效果最好。

(a)原始特征
2.5 消融实验
为了证明本文算法的有效性,将残差变换模块替换为直接下采样开展对比实验。多尺度特征可以压缩为单尺度特征进行编码传输,其中最简单的方式就是用双线性插值下采样将多尺度特征尺寸规范化,然后按通道拼接,再做编码传输。
为了便于对比,将残差变换模块直接替换成双线性插值下采样,用双线性插值上采样代替对应的预测重建模块,算法的其他部分保持不变,计算得到的结果见表2。可以看到,在传输码率基本一致时,残差变换模块的加入令CI框架表现出更强的检测能力。
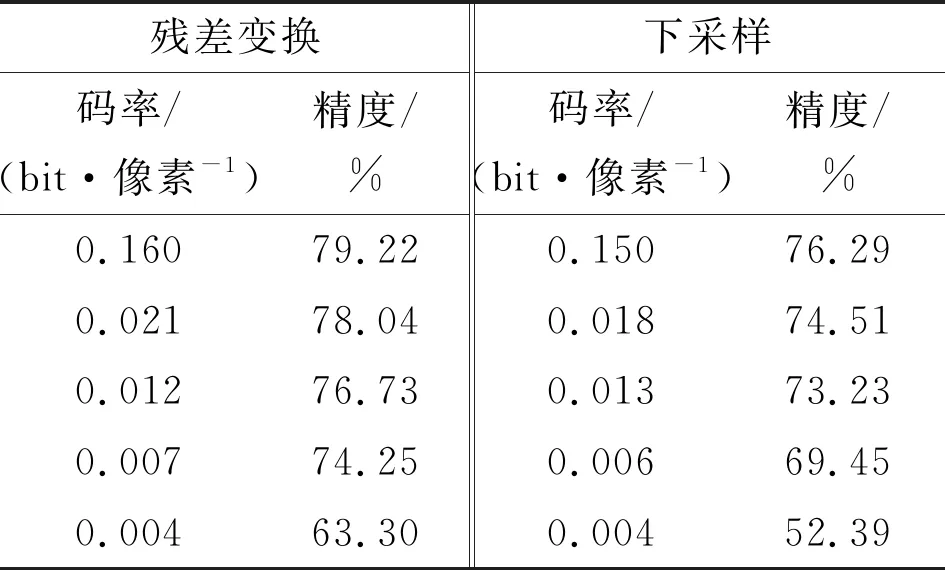
表2 直接下采样与残差变换模块特征压缩效果对比
接着,开展消融实验进行复杂度分析,分别测试了CI框架的推理时间和运算量,结果见表3。虽然在CI框架中插入残差变换模块导致整体计算量有所增加,但在相似的码率下,残差变换模块对协作推理性能的提升超过了3%。因此,相比于压缩性能的提升,残差变换模块带来的额外计算量可以接受。

表3 插入下采样与残差变换模块CI框架复杂度对比
2.6 泛用性验证
本文算法针对中间特征进行编码传输,可以移植到各种多任务网络,根据压缩前后的多尺度特征差异进行联合优化,具有泛用性。因此,将其应用于广泛使用的多任务网络模型Mask RCNN,分别开展目标检测和语义分割性能测试,完成泛用性验证。
实验设置与Faster RCNN网络模型相同,为了观察多任务网络经过特征压缩后推理能力的衰减情况,定义预测误差为未压缩预测结果和压缩预测结果的平均精度之差,得到的结果如图8所示。
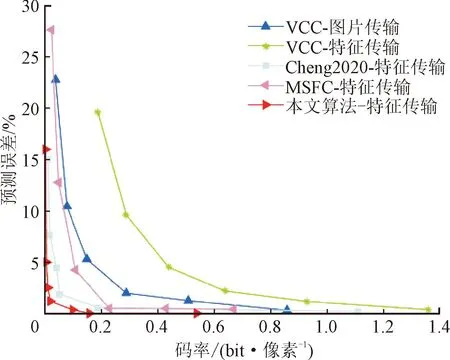
(a)目标检测任务的预测误差
以上实验结果表明,本文算法可以用于多任务网络,在多个任务上都具备良好的压缩性能。在低码率场景下,本文算法的信息损失更慢,表明其在多任务网络中也可以进行特征压缩。
3 结 论
针对协作智能框架复杂网络中间特征数据量大、难以高效传输的问题,提出了一种面向机器视觉任务的多尺度图像特征压缩算法,将残差变换模块与自编码器的联合压缩优化,实现了对多尺度中间特征的高效压缩。通过仿真实验,得到以下结论。
(1)在相同的特征压缩比下,本文算法重建的多尺度特征表达能力最完整。当压缩中间特征的数据量为原始特征数据量的0.91%时,依然能够正常完成DNN网络的推理任务。
(2)相较于已有的传统图像编码和深度特征编码算法,当传输码率为0.02 bit·像素-1时, 本文算法DNN网络的推理精度损失不超过2%;当码率为0.1 bit·像素-1时,不同压缩算法下特征可视化重建的对比结果表明,本文算法在细节上能与原始特征保持一致,重建效果最好。
在云边协作智能框架中,对中间特征的高效压缩和传输是提高框架效率的核心问题,本文算法具有良好的特征压缩和编码传输性能,能够提高云边协作智能框架的应用效率。此外,开展的泛化性实验表明,本文算法解码特征具有一定的泛化能力。
