基于RUN 优化算法的波前校正系统
2023-12-18杨慧珍臧祥栋张之光刘金龙
杨慧珍,臧祥栋,张之光,刘金龙
(1 江苏海洋大学 电子工程学院,连云港 222005)
(2 金陵科技学院 网络与通信工程学院,南京 211169)
0 引言
光透过畸变介质或者不完备的成像系统后会产生静态或动态畸变,严重影响光学系统的成像性能。自适应光学(Adaptive Optics,AO)[1-3]技术是校正波前像差的重要技术手段,已用于多个领域,如显微成像[4]、人眼视网膜成像[5]、内窥镜[6]、光束整形[7]及天文成像[8]等。自适应光学系统按照原理可以分为两大类,即常规自适应光学系统和无波前探测自适应光学系统。常规自适应光学系统因为存在波前传感器,使得自适应光学系统成本高,结构复杂。对于要求结构小型化的领域,常规自适应光学系统已不能满足应用需求。无波前探测自适应光学系统由于不需要波前探测环节,系统结构简单,便于实现,且可应用于常规自适应光学系统无法工作的应用环境,近几年得到了广泛研究。系统控制算法是决定无波前探测自适应光学系统校正性能的关键因素。
现有无波前探测自适应光学系统控制算法大致可分为三类:基于种群优化的元启发类,如遗传算法(Genetic Algorithm,GA)[9-10]、粒子群优化算法(Particle Swarm Optimization,PSO)[11-12]和差分进化算法(Differential Evolution Algorithm,DEA)[13]等;基于数学原理的梯度下降类,如随机并行梯度下降(Stochastic Parallel Gradient Descent,SPGD)算法[14]及其各种变形[15-17];基于物理原理的模型式[18]及其改进算法[19-21]。三大类方法在自适应光学系统控制中均有所应用,各有其优劣势,比如元启发式算法收敛速度相对慢,但全局收敛性好;SPGD 方法收敛速度相对快,但全局寻优能力差;模型类算法收敛速度最快,但是需要大量预处理。
太阳已经升起来,殷明站在大街上,透过手掌抬头望着这个迟迟不肯升起的火球,发出耀眼刺目的光线,光线穿过指缝映在苍白的脸上暖暖的、柔柔的、轻轻的。这光线像是一根燃起的火柴,点亮了心底死寂枯萎的心房,闪现着微弱、黯淡、忽隐忽现的光亮。
AHMADIANFAR I 等于2021 年提出龙格-库塔优化器(RUNge Kutta Optimizer,RUN)[22]。作为一种新兴的元启发式算法,RUN 算法是一种无隐喻的种群优化方法,运用四阶龙格-库塔(Runge Kutta,RK)数学方法计算梯度进行种群的优化[23]。以该方法作为全局搜索逻辑,能够有效地探索和搜索空间中的目标区域。RUN 优化算法能处理各种优化问题,目前,已经成功运用到热力学[24]和电力工程[25]等工程领域。本文提出将基于种群优化的RUN 优化算法用于自适应光学系统控制,考察基于RUN 的自适应光学系统波前校正性能。
以61 单元变形镜作为波前校正器件,不同湍流强度下的畸变波前作为校正对象,建立基于RUN 优化算法的自适应光学系统模型。通过点目标成像模拟实验,对比分析基于RUN、PSO、DEA 和GA 的波前校正系统在不同湍流强度下的校正效果和校正速度,以及陷入局部极值的情况。
当算法满足校正要求或者预先设置迭代条件时,可得到全局最优控制信号。将该信号经过数模转换、放大施加到波前校正器,完成波前畸变校正。算法不满足终止条件时,继续执行优化算法,进行下一次迭代。基于RUN 的AO 系统控制方法流程如图1。
1 基于RUN 的AO 系统控制方法
以波前校正器的驱动电压作为控制信号时,粒子位置代表校正器的驱动电压。算法迭代过程中,种群粒子在搜索空间中探索和开发。假设波前校正器的驱动器单元数为M,则驱动器电压的求解转化为一个M维优化问题,基于RUN 的AO 系统控制方法包括以下三个阶段。
初始化阶段。设置种群大小为N,每一个个体都是M维的粒子,粒子的初始位置Xj,M(j=1,2,…,N)通过式(1)确定。
根据DM 补偿原理,补偿相位由DM 各驱动器的影响函数线性组合而成,可表示为
位置更新阶段。当R≥0.5(R为[0,1]之间的随机数),粒子根据开发结果产生新位置;否则粒子根据探索结果产生新位置。为了保证解的质量,经过解质量增强(Enhanced Solution Quality,ESQ) 环节,避免每次迭代中陷入局部最优,从而进一步寻优。为实现适当的全局和局部搜索,使用四阶RK 方法作为探索和开发的主要搜索机制。设目标函数为y(x),x是M维粒子,即粒子的位置,对应波前校正器驱动电压向量。四阶RK 公式基于四个系数的加权平均值,表示为
式中,k1、k2、k3、k4四个系数因子分别为
用反映光斑弥散程度的性能指标-平均半径(Mean Radius,MR)作为优化算法目标函数,MR 表达式为
以往的临床医学检验中,在对标本进行尿液白细胞检验的时候,往往都会采用尿液干化学法来进行检验,采取尿液标本,并将检测试纸放入尿液标本中,尿液化学成分会使试纸内的发色模块产生反应,然后再采用尿液分析仪器来对试纸的检验结果进行分析,从而得出准确的尿液白细胞检验结果。在对泌尿系统疾病患者进行医学检验的时候,通常都会采用该检测方式,但是在实际检测的过程中,很容易受到各种因素的影响,从而导致检验结果的准确性下降,进一步影响医护人员对患者病情的判断,很容易导致误诊、漏诊现象的发生,非常不利于患者病情的康复,严重的甚至会导致医患纠纷的发生。
2、缺乏自信心,意志不坚定。中职生在以前的初中已经被冠以“差生”头衔,很少得到老师的表扬和同学的尊重以及肯定,认为自己不行,在严重缺乏自信的情况下使他们越来越不愿意学习,甚至害怕学习,这样的心态,何谈学习积极性。

图1 基于RUN 的AO 系统控制方法流程Fig.1 The flow of RUN optimization algorithm
2 基于RUN 优化算法的波前校正系统
基于RUN 优化算法的波前校正系统如图2,以61 单元变形镜(Deformable Mirror,DM)作为波前校正器,以电耦合元件(Charge Couple Device,CCD)作为图像传感器。系统主要由DM、CCD、透镜、控制模块、图像采集卡、数模转换器、高压放大器组成。当光波通过随机介质时,入射光波发生畸变,畸变后的入射光经过变形镜反射,通过聚焦透镜到达CCD 相机成像。基于RUN 的AO 系统控制方法利用图像采集卡采集的图像数据计算DM 的控制信号。数模转换器将数字控制信号转换为模拟信号,再由高压放大器将控制信号放大后施加到变形镜,完成一次闭环校正。其中61 单元DM 驱动器排布位置如图3,驱动器之间呈三角形分布。
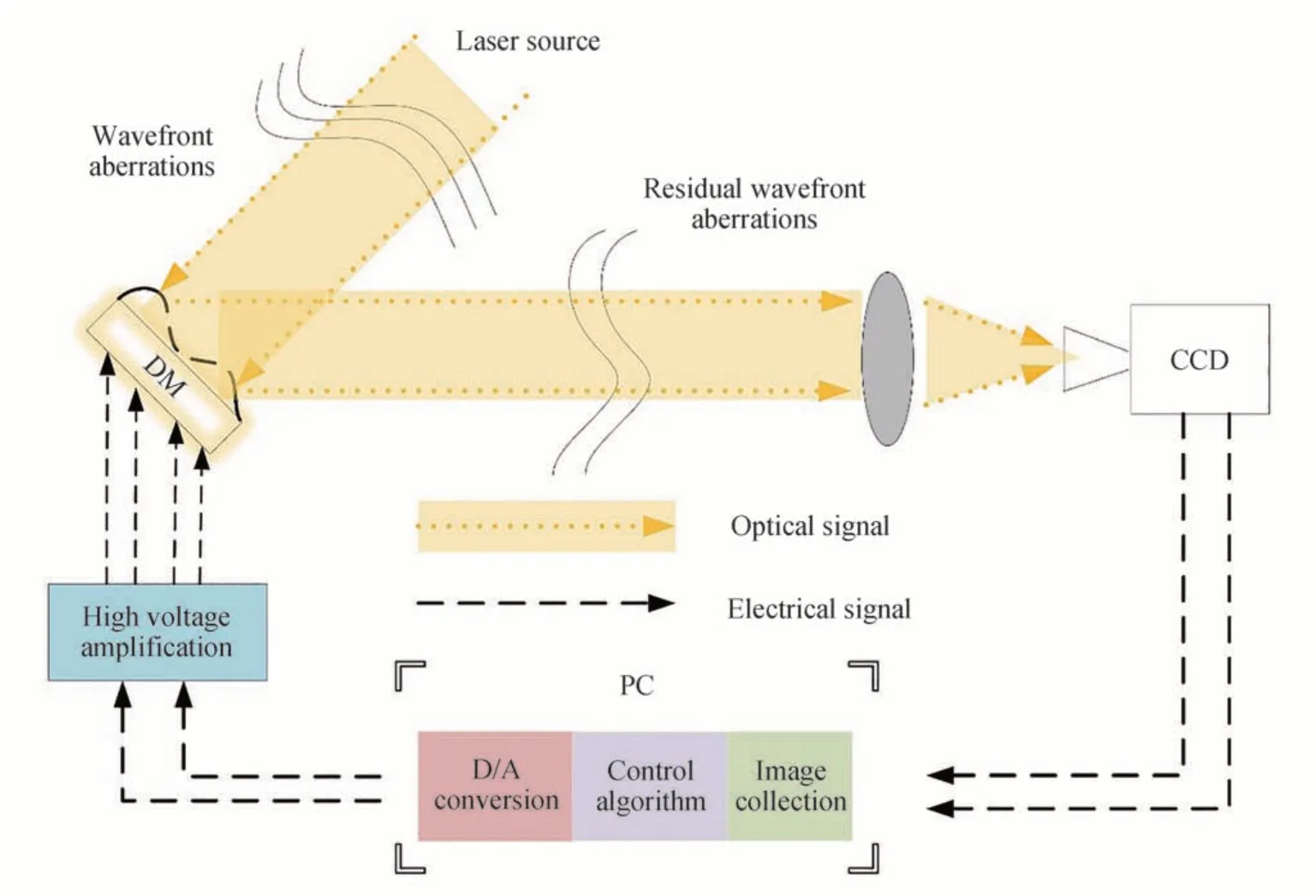
图2 无波前探测自适应光学系统Fig.2 Wavefront sensorless adaptive optics system

图3 61 单元变形镜驱动器位置分布Fig.3 The driver distribution of 61 element deformable mirror
式中,UM和LM分别是M维搜索空间的下边界和上边界,R是[0,1]范围内的随机数。将种群初始位置作为控制参数施加到波前校正器,再通过图像采集卡将图像传感器信息读入控制模块。把表征波前畸变程度的性能指标作为优化算法的目标函数,计算目标函数值。分析出目前全局最优解xgbest。
我国大力打造绿色生态环境建设,坚持生态产业化、产业生态化,尤其重视对生态环境的整体建设,绿化种植业得到了前所未有的发展。为此,探究林业苗木种植死亡的原因,并提出相应解决方法,这点很重要。分析了林业苗木种植死亡的原因,提出了有效的解决方法,希望为林业苗木种提供必要的参考。
秦铁崖道:“秦某无意蹚浑水,不过,惩奸除恶,扫荡八虎,秦某甘当马前卒,刀山火海也敢上,龙潭虎穴照样闯。”众人肃然起敬。
|(u,v)-(u′,v′)|为光斑坐标(u,v)与平面质心(u′,v′)之间的距离,I(u,v)是畸变波前对应的远场光斑光强分布。随着AO 系统校正过程的进行,像差变小时,MR 值也逐渐变小。记录算法迭代过程中的MR值,为便于分析同时也记录相应的斯特列耳比(Strehl Ratio,SR)值的变化情况。
校正阶段。完成种群中每个粒子的位置更新并修正xgbest。将xgbest经过数模转换、放大施加到波前校正器,校正残余波前,完成一次迭代。
式中,(u′,v′)是像平面质心坐标,计算公式为
式中,qi是第i个驱动器的控制信号,Qi(x,y)是第i个DM 驱动器影响函数。(x,y)是波前平面上的坐标,(xi,yi)是DM 第i个驱动器上的坐标,z是驱动器间距,A是驱动器之间的耦合值,b是高斯指数,实际测量A=0.08,b=2。采用RODDIER A N[26]所提出的方法生成相屏模拟畸变波前,不同相屏之间符合Kolmogorov 功率谱模型,各相屏之间不存在相关性。相屏由3~104 阶Zernike 像差组成,不包括倾斜项。湍流对望远镜成像的影响用D/r0表示,D是望远镜口径,r0是大气相干长度。D/r0值越大,表明光波受湍流影响越大。
3 仿真结果与分析
分别设置 RUN、PSO、DEA 和GA 四种算法的种群数N为50,并在每个湍流强度下设置相同的搜索空间。根据各算法的大量模拟实验结果,选出每种算法各湍流情况下的最优参数,并将最大迭代次数设置为500。
3.1 校正能力对比
仿真过程中,分别选取D/r0=5、D/r0=10 和D/r0=15 三种不同湍流强度下各100 帧随机波前像差作为校正对象,RUN、PSO、DEA 和GA 四种算法在三种不同湍流强度下最终校正效果如图4。为便于分析四种算法校正效果,图4 同时给出了初始平均SR 值(Initial)和61 单元DM 理想校正后的平均SR 值(Ideal)。

图4 不同湍流强度下初始、理想SR 和RUN、PSO、DEA 和GA 校正后SR 的比较Fig.4 Comparisons of SR of the initial,the ideal,by RUN,PSO,DEA,and GA under different turbulence levels
从图4 中可以看出随着湍流强度的增加,校正能力稍有下降,但四种算法均都获得了较好的校正效果。RUN 算法和GA 算法校正效果接近,明显优于PSO 和DEA。RUN 算法和GA 算法相比,前者略优于后者。RUN 算法的收敛结果最接近于不同湍流条件的61 单元变形镜的最大校正能力。校正能力有所下降,这是因为对于固定单元数的变形镜来说,其最大校正能力是有限的。湍流强度越小,校正结果越接近理想校正。
3.2 校正速度对比
仿真过程中,分别以D/r0=5、D/r0=10 和D/r0=15 不同湍流强度下各100 帧随机波前像差作为校正对象,分析RUN 算法、PSO、DEA 和GA 四种控制算法的收敛速度。100 帧随机像差的平均校正结果作为实验结果,四种算法各迭代500 次。平均MR 和平均SR 曲线如图5。

图5 分别以RUN、PSO、DEA 和GA 作为控制算法,自适应光学系统在不同湍流强度下的平均自适应过程Fig.5 The adaptation process of the adaptive optics system under different turbulence levels using RUN,PSO,DEA and GA as control algorithms,respectively
从图5 可以看出,各算法500 次迭代后均已经充分收敛。对比图5 中不同湍流条件下的收敛曲线可以发现,随着湍流强度的增加,不同算法收敛所需要的迭代次数均有所增加。主要是因为湍流影响增大,像差的高频分量增加,寻优的空间空大,导致收敛时间增加。但是,对比同一湍流条件下的不同算法的收敛曲线可以发现,基于RUN 的自适应光学系统收敛速度明显快于其他三种控制算法的自适应光学系统。根据仿真结果定量分析不同湍流条件下不同控制算法的收敛速度。
以单一有机体系作为溶剂,溶解纤维素并催化转化制备5-HMF过程中,虽然具有成本较低、反应周期较短等优点,但一般需要高温高压的条件;且生成的5-HMF易热解,导致得率较低,部分有机溶剂环境污染问题较严重,不符合绿色化学的理念。
目前,医学院校计算机基础教学难以适应计算机技术在医学领域广泛应用的新形势,存在着课程地位认识不足、教学内容支撑专业应用和社会应用力度不够、质量评价体系有待改进等方面的问题。只有积极思考和探索具有医学特色的计算机基础教学改革,以培养医学生的计算思维能力为主要任务,使其具有利用计算科学对医学相关问题进行分解、提炼归纳、系统设计的能力,为计算机学科与医学相关学科的交叉融合做好必要的知识储备和应用能力的铺垫。
系统收敛速度是判断该算法能否实际应用于自适应光学控制的一条重要准则。三种不同湍流条件下,平均SR 初始值分别为0.246、0.01 和0.055,RUN 优化算法校正后最终SR 平均值分别为0.954、0.868 和0.726。不同湍流强度下RUN 控制算法 SR 校正范围的80%分别为0.813、0.714 和0.592,以此作为判断标准,分析四种算法达到同一校正效果时所需要的迭代次数,结果如表1。

表1 RUN、PSO、DEA 和GA 校正速度对比Table 1 Comparison of correction speed of RUN,PSO,DEA and GA
由表1 可以看出,湍流强度为D/r0=5 时,RUN 相比PSO、DEA 和GA,校正速度分别提高了约4.45、3.25、3.45 倍;D/r0=10 时,校正速度分别提高了约3.90、3.84、4.10 倍;D/r0=15 时,校正速度分别提高了约3.79、3.37、5.26 倍。即,在取得相同校正效果时,基于RUN 优化算法的波前校正系统在不同湍流条件下的校正速度均提高了三倍以上。
3.3 陷入局部极值情况分析
取湍流强度为D/r0=10 下的一帧随机波前像差作为校正对象,分析RUN、PSO、DEA 和GA 陷入极值情况。RUN、PSO、DEA 和GA 各自随机运行100 次的MR 变化曲线分别如图6 (a)、(b)、(c)、(d)所示,SR变化曲线分别如图6 (e)、(f)、(g)、(h)所示。由图6 可以看出,RUN 和GA 的100 次随机运行迭代后均收敛到全局极值,PSO 收敛到全局极值附近,DEA 在100 运行中有3 次陷入局部极值,且RUN 算法与GA 相比,具有更好的收敛稳定性,鲁棒性更优。

图6 同一帧像差随机运行100 次,四种算法的MR 和SR 收敛曲线Fig.6 MR and SR curves of four different control algorithms when stochastic correction is performed on the same aberration for 100 times
另外,本文还以127 单元变形镜作为校正器件,对基于RUN 优化算法的自适应光学系统校正能力进行了模拟和分析。结果发现四种算法收敛速度变慢,收敛精度都有所提高。总体来说,RUN 算法相对于PSO、DEA 和GA 的收敛精度和收敛速度优势和61 单元变形镜的结论类似。收敛速度变慢的原因在于待求解的未知参数由61 个增加到127 个。收敛精度提高的原因在于变形镜单元数增多,校正能力增强。
易非气得掀了被子,侧过身去。他们怎么能无耻到这种程度呢?他们不知道这房子是她买的吗?她咬碎了牙齿省吃俭用买的房子,他们竟然想就这样占了去?我这真是引狼入室啊!
4 结论
本文将基于种群优化的RUN 优化算法用于自适应光学系统控制,考察基于RUN 的自适应光学系统波前校正性能。RUN 算法运用四阶RK 方法作为主要搜索机制,使搜索梯度的方向更加准确,其位置更新阶段中ESQ 环节又进一步加强了搜索解的准确性,避免每次迭代中陷入局部最优情况,从而使RUN 算法能够更快地搜索到最优解。与PSO、DEA 和GA 相比,RUN 算法的收敛结果最接近于不同湍流条件的波前校正器所能达到的最佳校正能力;在取得相同校正效果时,基于RUN 优化算法的波前校正系统在不同湍流条件下的校正速度均提高三倍以上且全局收敛性最好。多次模拟实验发现所提出的控制算法对参数不敏感,更便于实现。研究结果为基于RUN 优化算法的波前校正系统的实际应用提供了理论基础。当把基于RUN优化算法的无波前自适应光学系统用于对校正速度有要求的应用环境时,可以采用硬件实现算法,如GPU、FPGA 等进行加速。
