金刚石压砧内单晶硅高压折射率的椭偏测量
2023-12-18鲍晓艳邓硕吕海飞黎敏
鲍晓艳,邓硕,吕海飞,黎敏
(武汉理工大学 理学院,武汉 430070)
0 引言
压力可导致物质的晶格结构改变[1],进而引起包括电子能带结构在内的多种物理、化学、机械性质发生改变。但是很多物质的高压相在常压下无法保持,因此,高压原位(in situ)测量技术是理解高压下物质结构及其转变的关键手段。现有的高压加载技术中,金刚石对顶砧(Diamond Anvil Cell,DAC)通过施加在面积极小但硬度极高的金刚石砧面上的压力产生极大的压强,是目前唯一能够实现1 000 GPa 以上压力的静高压装置[2]。DAC 技术在不断发展过程中,通过改善切割倒角、改进垫片材料和引入传压介质等,不断提升实验极限压力,极大地促进了高压实验技术的发展。同时,因金刚石从远红外至ϒ 射线电磁波谱区都具有良好的透光性,因此,具有易与光学测试技术结合的先天优势。目前,拉曼光谱[3-7]、同步X 光辐射[8-10]、紫外/可见光/红外光谱[11-15]等商用仪器均已被用于原位探测高压下材料性质的变化。然而,以上基于特征光谱吸收的高压原位测量方法均无法获取材料的光学常数,或者说更准确地描述材料性质的变化过程。椭偏测量技术作为一种代表性的光学测试手段,可准确测量薄膜的介电常数(及厚度)。但是,受到DAC 小入射孔径和小样品尺寸(百微米量级)的结构限制,商业椭偏仪无法实现直接测量。而由于高压环境的特殊性,国际上针对DAC 结构的椭偏测量研究偏少。NISSIM N 课题组在2009 年和2011 年分别报道了采用单一波长椭偏法测试铁的光学常数的结果[16,17],观察到了铁的相变。国内华中科技大学在现有椭偏仪上增加会聚透镜,并且对DAC 装置进行扩大测量角度的改造加工,得到铁在320~1 690 nm 波段的椭偏参数和10 GPa 内拟合的光学常数[18]。因此,需要一种面向DAC 结构设计的椭偏测量装置以实现高压下材料光学常数的原位监测。
单晶硅作为应用最广泛的半导体材料,是现代集成电路行业和微光学加工中最常见基底材料[19,20],其常压下的光学性质已非常清晰。然而,硅晶体在高压加载下会发生一系列相变并金属化,其物理性质也会随之而变化,其中的过程目前并不清楚,缺乏物性常数和有效的监测手段。而光学常数恰好可用以记录此一系列变化过程。获取单晶硅在不同压力加载下的光学常数信息能够进一步推算其电导率等电学参数。同时,硅作为常用的光学衬底材料,其压力加载下光学常数的变化规律也是研究材料在高压下性质的基础。本文通过自主设计的斯托克斯椭偏测量系统,实现适用于常规DAC 装置的小角度多波长椭偏参数测量,结合光学建模,获取不同压力下单晶硅的光学常数。本文采用的椭偏法与高压加载技术相结合的测量方法,可以作为获取高压加载下物质光电性质的有力工具。
1 高压椭偏法原理
1.1 椭偏测量原理
偏振测量利用光束经过样品前后偏振特性的改变获取样品折射率、表面粗糙度等信息。如图1 所示,通过分析入射光与出射光的偏振态,定义样品的椭偏参数ψ和Δ。

图1 偏振测量原理示意图Fig.1 Schematic diagram of polarization measurement principle
式中,ρ为p 偏振光和s 偏振光的反射系数rp和rs之比,Δ为p 偏振分量和s 偏振分量反射前后的相位差之差。实验中测量获取的椭偏参量ψ为角度值,此值与光线的入射角度、波长以及薄膜的光学常数和厚度等信息相关。椭偏测量分析流程如图1(b)所示。根据偏振矩阵运算表达式(2),得到输出光的斯托克斯矢量Soutput为
式中,Si(i=0,1,2,3)依次表示总的入射光强、x分量和y分量的光强差、+45°和-45°偏振分量光强差、左旋和右旋圆偏振分量光强差。本文使用斯托克斯偏振测量仪得到样品反射光的椭偏参数。设置入射光具有特定偏振态S=(1,0,1,0),待测样品为各向同性。此时,测量得到反射光的斯托克斯矢量即可计算得到样品的椭偏参量ψ和Δ。
不同波长下,薄膜光学常数值与椭偏参数存在确定的对应关系,此为椭偏参数的数值拟合与光学常数反演问题。而通过椭偏参数拟合获得样品光学常数的关键在于DAC 压腔内光学模型的建立,并通过式(4)的均方差函数评价光学常数拟合结果。
1.2 DAC 高压光学模型的建立
高压椭偏测量不同于常规椭偏仪测量时的薄膜样品暴露于空气中,如图2 所示的DAC 结构与光路。待测样品所在高压区域为全密闭环境,入射光需经过数百微米尺度的金刚石窗口到达样品界面,因此需建立对应的光学模型(如图3 所示)反演样品光学常数信息。

图2 DAC 结构及光路反射示意图Fig.2 DAC structure and optical path reflection diagram

图3 适用DAC 内的多层膜反射示意图Fig.3 Schematic diagram of multilayer reflection in DAC
因金刚石(N2层)的厚度在毫米级,所以上部金刚石的上、下两表面(N1N2界面和N2N3界面)的反射光和并不相干,且可以将两束光分离,分别作为参考光和信号光进行分析。第一束(金刚石上表面N1N2界面)反射光仅包含金刚石的折射率信息,第二束反射光与射可依据菲涅尔公式推导得出;而在两层膜以上的模型中,由于膜层增多,反射和透射过程变复杂,采用矩阵理论分析更便捷。设用一个列矩阵表示准单色波的偏振特性,即之和包含样品折射率信息。N1N2界面反
式中,Ep和Es为直角坐标系中电场的p 和s 方向分量,E0p和E0s为电场分量的初始值,δ1和δ2为两分量的相位。光束在分界面上的反射或折射的过程可统一用式(6)和(7)表示,分别用i,r,t 角标表示入射、反射与透射光
式中,rp与rs,tp与ts分别为菲涅尔公式求得的各界面反射与透射系数。光束通过厚度为d的各向同性薄膜的传输过程可表示为
如图3 所示的多层膜光束传输示意图,运用式(9)矩阵运算模拟光传输过程,其中矩阵J表示界面透射、反射过程,分别用上标t,r 表示,下标表示光界面传输,矩阵M表示界面内传输过程,下标表示界面材料。高压界面反射光即R2可由式(10)表示,并由式(11)求解得到椭偏参量理论值。
另外,考虑金刚石表面存在不均匀粗糙层,对椭偏参数测量有一定影响。本文借助等效介质理论进一步分析。假设两种介质的不规则界面等效为一层有固定折射率和厚度的表面光滑薄膜,此薄膜对椭偏参数的影响与表面粗糙度等效。则最终光学模型为金刚石-等效膜层-样品三层膜结构。
为避免红宝石颗粒造成的界面不平整及易压碎硅片问题,本文通过金刚石拉曼进行压力标定[21]。本文采用拉曼光谱测试仪器测量金刚石表面拉曼峰,经过一阶求导后记录一阶最小峰值位置,并使用对应公式进行压力值换算,即
式中,Δω和ω0分别代表频率偏移、常压下的频率,A,B为拟合参数值。
单晶硅的高压拉曼光谱测量实验采用加装50 倍长焦镜头的拉曼光谱仪(SYC1227-4218F,HORIBA),将波长532 nm 的激发光聚焦于DAC 内单晶硅表面,采样时长为3 s,记录采样光谱范围为300~800 cm-1的数据并完成光强归一化处理,即获得对应压力下的单晶硅的拉曼光谱。
1.3 椭偏测量系统
图4 是本文设计的高压椭偏测量系统图。从右到左依次为光源(Light source)、衰减滤波器(Filter)、光束调理系统,包括反射镜(Reflector)、格兰泰勒棱镜(Glan-Taylor polarizer)、会聚透镜(Focal lens)、DAC 平台(电动微位移、旋转平台及相关旋转控制系统)和偏振测量仪(Polarization analyzer)。由于DAC 的柱形结构,实验中的椭偏测量装置采用卧式,即入射和出射DAC 的光平行于光学平台。超辐射白光激光器(SCpro,安扬激光)发出的宽谱光经过声光滤波器(单波长输出带宽2~10 nm)输出;光束通过直角棱镜两次反射实现光路转折后,经格兰-泰勒棱镜输出特定方向线偏振光,再经由会聚透镜聚焦于压砧内的样品表面;可调焦成像系统CCD 相机用来确认光斑聚焦位置。入射光分别经DAC 的金刚石上下表面反射后,有两束反射光,在偏振测量仪(PAX1000VIS/M,Thorlabs)之前配置合适的狭缝,即可分别测量两束反射光的偏振态。

图4 原位高压椭偏测量系统示意图Fig.4 Schematic diagram of in situ high pressure ellipsometry measurement system
实验用高压椭偏测量系统中,光源的输出光斑大小约为2.1 μm,测量光谱范围为450~700 nm;伺服电机控制电动转台可实现0.04°的入射角度调节;紧凑型五轴微位移平台控制聚焦透镜,可实现x、y、z三轴3 mm 量程和俯仰角±3.5°调节。
受DAC 腔体尺寸的限制,测试样品厚度需控制在几十微米以下,而市售单晶硅片的厚度均大于100 μm。图5 为单晶硅样品制备流程图。将单面抛光带25 nm 氧化层的单晶硅片,用金刚石砂纸打磨至30 μm 左右,使用激光切割为直径180 μm 的圆片,清洗干燥后立即装填至压腔内,避免进一步氧化。使用铼片打孔在金刚石之间形成高压腔体,单晶硅抛光面紧挨金刚石一侧,并填充氯化钠粉末作为传压介质。

图5 单晶硅制备流程图Fig.5 Flowchart of monocrystalline silicon preparation
2 测量结果与讨论
在进行DAC 高压椭偏测量前,首先使用椭偏测量系统对未加载压力(开放DAC)的单晶硅片进行椭偏测量,以验证实验系统的有效性。实验完成了入射角度分别为27°、30°、33°和40°的椭偏参数的测量(如图6所示)。然后,利用所建立的光学模型拟合得到单晶硅折射率,与椭偏仪VASE-V 的测试结果及文献中Schinke 测量结果[22]对比(如图7 所示)。结果表明,在400~700 nm 常压下单晶硅折射率测量结果与商用椭偏仪测量结果一致,这种一致性可证明本测量系统的可靠性。

图7 折射率实部对比结果Fig.7 Comparison result of real part of refractive index
高压下的椭偏测量包括金刚石上、下界面反射光的斯托克斯参量测量和使用金刚石拉曼光谱标定压力两个步骤。DAC 未加压前,金刚石与单晶硅之间存在空气间隙,旋紧加压螺母的过程中,空气间隙减小,通过50 倍物镜成像观测到彩色干涉条纹消失判定空气间隙可忽略(此时完成预压约为2 GPa 左右)。图8 为2~9 GPa 下单晶硅椭偏测量结果。图9 为与之对应的单晶硅的拉曼光谱的测量结果,可看到单晶硅的拉曼峰随着压力增大而红移,这与压力导致单晶硅晶格常数减小现象一致。
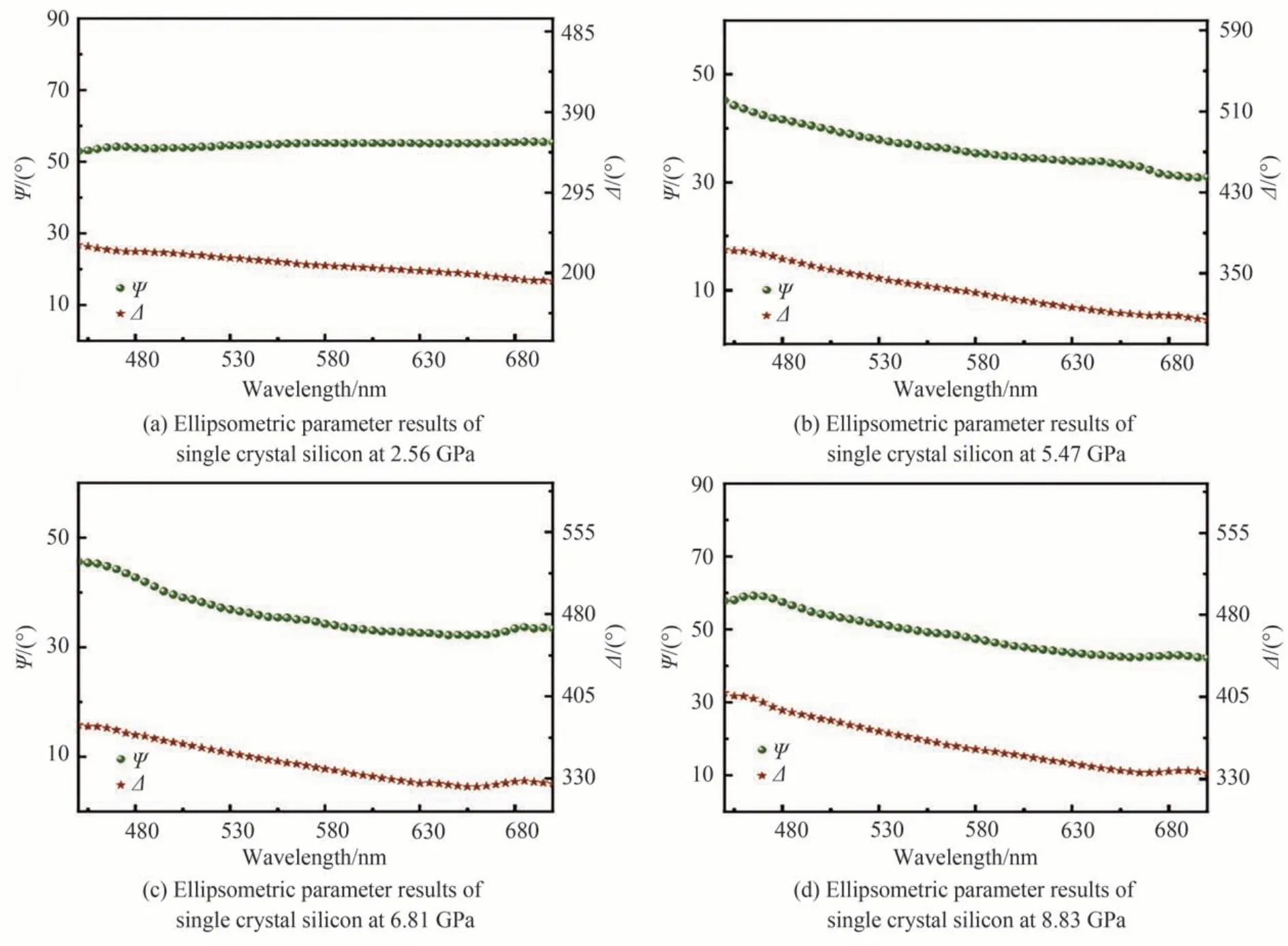
图8 不同压力下单晶硅椭偏参量结果图Fig.8 Ellipsometry parameter results of monocrystalline silicon under pressure loading
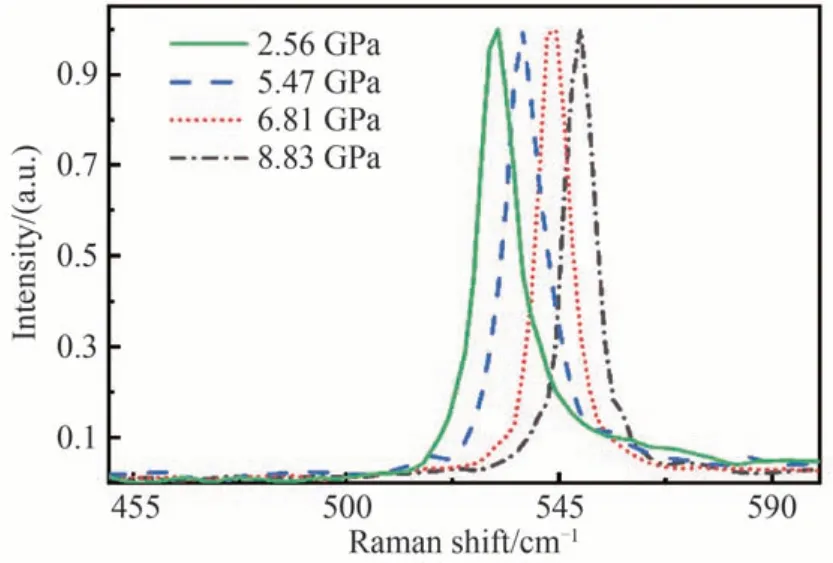
图9 压力加载下单晶硅拉曼测量结果Fig.9 Raman measurement results of monocrystalline silicon under pressure loading
参考图2(b)所示金刚石的反射光路,本文假设金刚石的上下两反射面的反射光束是完全分离的,因此,2.2 节中膜层理论所引入的椭偏参量值仅考虑金刚石的上表面或下表面的反射光。而实际测量过程中,由于受DAC 角度限制,通过狭缝进入偏振测量仪分别检测的两光束偏振信息中R1的反射率高于R2,因此,在进行R2光束椭偏测量时,受到R1的影响会引入误差。为此,在理论椭偏参量模型中引入校正参数模拟R1的影响。校正后的理论椭偏参量ψ与实验结果对比如图10 所示。校正后的椭偏参量与理论值基本相符。

图10 压力加载下单晶硅ψ 值实验仿真对比Fig.10 Comparison of experimental simulation of monocrystalline silicon ψ value under pressure loading
在实验测量波段450~700 nm,采用柯西色散模型进行遗传算法拟合分析,分别得到不同压力下单晶硅折射率实部数据如图11 所示。图中数据表明,随压力增大,单晶硅折射率整体呈现增大趋势。8.83 GPa 折射率拟合结果表明压力增加会导致单晶硅的色散情况加剧。

图11 压力加载下单晶硅折射率结果Fig.11 Refractive index of monocrystalline silicon under pressure loading
3 结论
采用斯托克斯椭偏测量系统,针对DAC 环境,实现了高压下小角度的椭偏测量。基于偏振测量的基本原理与高压加载技术,实验得到了2.56 GPa、5.47 GPa、6.81 GPa、8.83 GPa 压力加载下单晶硅材料的椭偏参数信息,并采用遗传算法分析拟合各压强值对应下单晶硅符合柯西色散模型的折射率结果。实验结果表明,随着压力的增加,单晶硅的折射率呈现增大的趋势,并且色散加剧。受限于目前的DAC 加工工艺,分别经过金刚石两反射面的光束存在一定程度相互影响,是本研究中测量误差的主要来源,有望通过金刚石界面加工工艺的改进,进一步减小这一误差,提升高压下光学常数测量的准确度。
